紧支撑样条小波插值及其应用

高忠社,何万生,谢保利

(天水师范学院数学与统计学院,甘肃天水 741000)

紧支撑样条小波插值及其应用

高忠社,何万生,谢保利

(天水师范学院数学与统计学院,甘肃天水 741000)

基于紧支撑样条小波函数插值与定积分的思想,给出了由紧支撑样条小波插值函数构造数值积分公式的方法.并将该方法应用于二次、三次、四次和五次紧支撑样条小波函数,得到了相应的数值积分公式.最后,通过数值例子验证,发现该方法得到的数值积分公式是准确的,且具有较高精度.

紧支撑样条小波函数;插值函数;数值积分

1 紧支撑样条小波函数

小波函数在众多科学领域得到了广泛的应用,如数值分析、信号处理、图像处理、微分方程数值解、量子力学、地质勘查、计算机视觉、机械故障诊断等,小波函数在数值分析中的应用是一个重要分支.通常大多数小波函数不能写出具体的解析表达式,而1992年文献[1]构造的紧支撑样条小波函数具有解析表达式,且该小波函数具有很多良好的性质,并被广泛的应用于众多科学领域.紧支撑样条小波是以B-样条函数作为尺度函数构造的.它具有很好的性质,如:有解析表达式、对称性、单正交性和消失矩等良好的性质[1-4].文献[4-5,7]讨论了紧支撑样条小波函数的性质,及插值函数,并证明了该插值函数具有唯一性,文献[8-9]讨论了三次紧支撑样条小波函数的插值并得到相应的数值积分公式,文献[10]给出了二次紧支撑样条小波函数插值及数值积分公式.在这里将主要讨论紧支撑样条小波函数的插值问题,并讨论紧支撑样条小波函数在数值积分方面的应用问题,给出了由紧支撑样条小波插值函数构造数值积分公式的方法,该方法为紧支撑样条小波函数在数值分析中的应用有一定作用,而得到的数值积分公式有一定的实用价值.

紧支撑样条小波函数ψm(x)是由m阶m-1次B-样条函数Nm(x)作为尺度函数,构造的m阶m-1次紧支撑样条小波函数ψm(x),ψm(x)函数具有解析表达式:

2 紧支撑样条小波插值函数

3 紧支撑小波插值函数的数值积分方法

3.1 三阶二次紧支撑样条小波插值

图1 尺度函数N3(x)的图像.

图2 尺度函数ψ3(x)的图像

3.2 四阶三次紧支撑样条小波插值

图3 尺度函数N4(x)的图像.

图4 尺度函数ψ4(x)的图像

对于四阶三次紧支撑样条小波函数ψ4(x)使用上面类似的方法,构造插值函数,建立数值积分公式,即有[8]

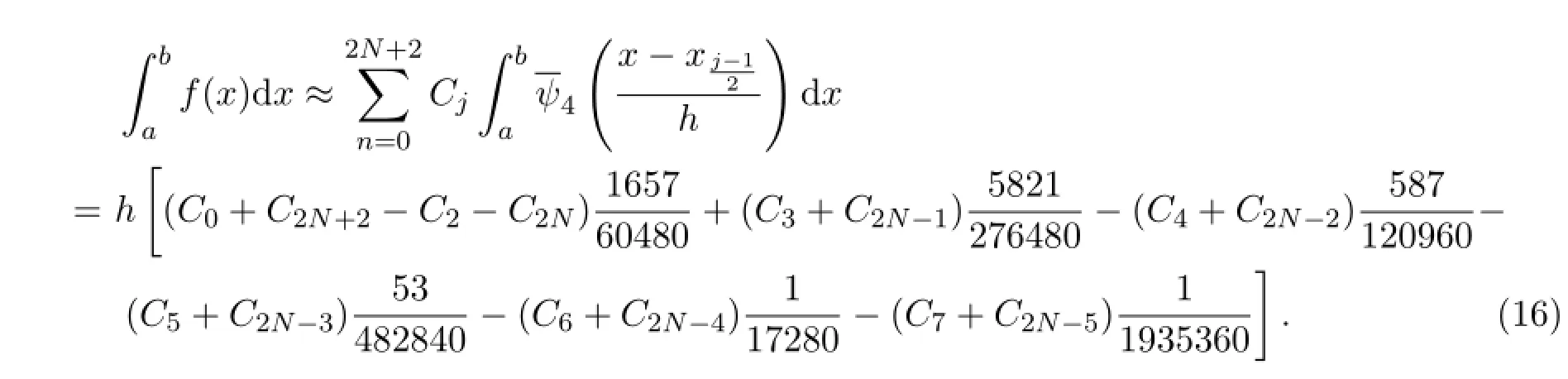
3.3 五阶四次紧支撑样条小波插值

图5 尺度函数N5(x)的图像.

图6 尺度函数ψ5(x)的图像

3.4 六阶五次紧支撑样条小波插值

当m=6时,ψ6(x)为六阶五次紧支撑样条小波函数,以五次B-样条N6(x)作为尺度函数构造的,其表达式为:

由于N6(x)是5次B-样条函数,ψ6(x)是五次分段多项式,而ψ6(x)的分段区间长度是N6(x)的一半,并且supp ψ6(x)=[0,11].尺度函数N6(x)和小波函数ψ6(x)的图像如图7,图8.

图7 尺度函数N6(x)的图像.

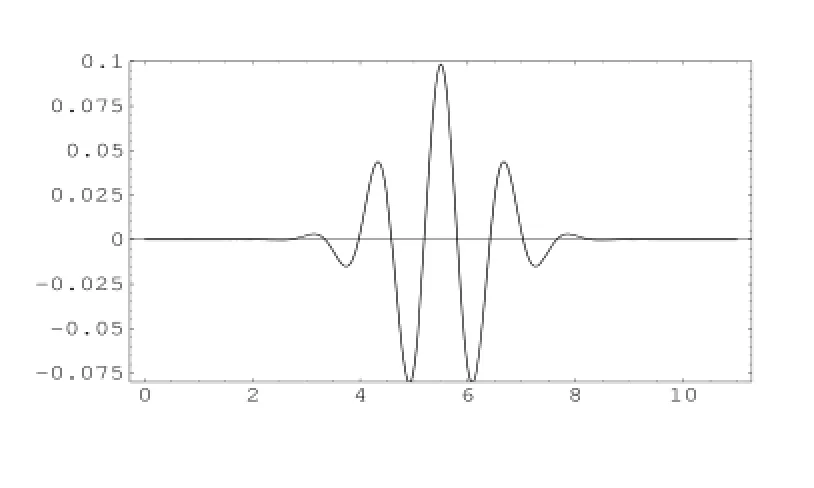
图8 尺度函数ψ6(x)的图像

同样的方法,可以得到更高次的紧支撑样条小波函数的积分插值公式.只不过是次数越高,求解的方程组的阶数的要求会越来越高,求解工作量也会越来越大.但是,得到公式的误差阶也会越来越高.根据定理2.2可知,

4 数值实验

计算

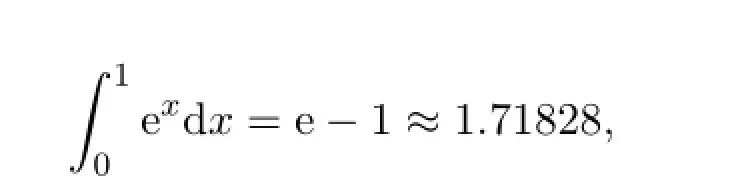
以N=40利用上面得到的公式进行计算,结果见表1:

文中由m阶m-1次紧支撑样条小波函数得到的数值积分公式,当函数f(x)的次数是不超过m-1的多项式时,该数值积分公式是精确的,对于一般的函数,误差阶可达到O(hm),但不足之处是,要求具有边界导数条件,并且数值积分公式中的系数是通过求解线性代数方程组得到的,由于紧支撑样条小波函数具有紧支集,故方程组的系数矩阵是带状稀疏的,使得计算变得相对容易;在误差方面,对于文中得到的数值积分公式,与常规的复化梯形公式和复化的辛普森公式相比较,发现文中得到的数值积分公式具有较高的精度.同时,通过数值例子说明得到的数值积分公式是正确有效的,且在数值积分中有一定的实用价值.

表1 数值积分结果

[1]Chui Charles K,Wang Jianzhong.On compactly supported spline wavelets and a duality principle[J].Trans. Amer.Math.Soc.,1992,330(2):903-915.

[2]Daubechies I.Orthogonal bases of compactly supported wavelets[J].Comm.Pure Appl.Math.,1988,41(7): 909-996.

[3]Mallat S.Multiresolution approximations and wavelet orthonormal bases of[J].Trans.Amer.Math.Soc,1989, 315:69-87.

[4]DanaˇCern´a,V´aclav Finˇek.Cubic spline wavelets with complementary boundary conditions[J].Applied Mathematics and Computation,2012,219(4):1853-1865

[5]金坚明.小波分析[M].兰州:兰州大学出版社,1993.

[6]孙家昶.样条函数与计算几何[M].北京:科学出版社,1982.

[7]金坚明,徐应祥,薛鹏翔.最小支集样条小波有限元[J].计算数学,2006,28(1):89-112.

[8]高忠社.数值积分的紧支撑样条小波方法[J].徐州师范大学:自然科学版,2006,23(2):22-25.

[9]杨渭清.多尺度紧支撑向量值正交小波的构造[J].纯粹数学与应用数学,2009,25(2):315-320.

[10]徐应祥.一类二次最小支集样条小波插值及其应用[J].合肥工业大学:自然科学版,2008,31(2):291-295

[11]王刚,吕军,袁丽霞.一类四元数小波包的构造[J].纯粹数学与应用数学,2011,27(5):570-576.

[12]何永滔.紧支撑正交的二维小波[J].纯粹数学与应用数学,2012,28(1):8-16.

The compactly supported spline wavelet interpolation and
its application

Gao Zhongshe,He Wansheng,Xie Baoli

(College of Mathematics and Statistics,Tianshui Normal University,Tianshui741000,China)

Based on the supported spline wavelet interpolation and defnite integral idea,the method of constructing the supported spline wavelets numerical integration formula is given.And with this method,the numerical integration formulas are got for the quadratic,cubic,quartic and quintic supported spline wavelets. Finally,it is proved through an example that the obtained formulas are correct and has a higher accuracy.

compactly supported spline wavelet,interpolation function,numerical integral

O24.82

A

1008-5513(2013)06-0591-10

10.3969/j.issn.1008-5513.2013.06.007

2013-10-01.

甘肃省教育厅科学研究基金(1108B-03).

高忠社(1979-),硕士,讲师,研究方向：小波分析及微分方程数值解.

2010 MSC:42C40