无8-,9-和10-圈的平面图的3-可选择性
朱晓颖
(南京航空航天大学金城学院,江苏南京 211156)
无8-,9-和10-圈的平面图的3-可选择性
朱晓颖
(南京航空航天大学金城学院,江苏南京 211156)
寻找平面图是3-或者4-可选择的充分条件是图的染色理论中一个重要研究课题,本文研究了围长至少是4的特殊平面图的选择数,通过权转移的方法证明了每个围长至少是4且不含8-圈,9-圈和10-圈的平面图是3-可选择的.
可选择的;平面图;围长
1 引言
本文中所考虑的图都是有限、简单的平面图,未定义的符号可参照文献[1].G=(V,E,F)表示一个平面图,V,E,F分别为其顶点集,边集和面集.NG(v)表示与顶点相邻的顶点集合,即顶点v的邻域.一个顶点的度

若d(v)=k,则称v是一个k-顶点,δ(G)为图中顶点的最小度.与f关联的边的数目(割边按两次算)记为面f的度数,记作d(f).若d(f)=k,则称f是一个k-面.设k是个整数,k+和k-分别表示大于等于k和小于等于k的整数.G中所有长为k的圈组成的集合记为Ck.若Ck=∅,则称图G是Ck-free.G中最短圈的长度称为G的围长.若两个面至少有一条公共边,则这两个面称为是相邻的.
定义1.1若与一个h-面相关联的所有顶点均为3--顶点,则称这个h-面为light h-面,否则如果它至少和一个4+-顶点相关联,则称它为non-light h-面.若f是一个non-light h-面,且b(f)上除了一个4+度点外,其余点均为3--顶点,则称此h-面为minimal h-面,否则,若h-面至少与两个4+-顶点相关联,则称此h-面为non-minimal h-面.
定义1.2对G中每个顶点v都分配一个颜色列表L(v),使得每个顶点能从其关联的色表中选色并且相邻的两个顶点选择不同的颜色,称为G的一个L-着色.若对图G的每个顶点的列表满足图G总存在L-着色,则称图G是k-可选择的.定义使得图G是k-可选择的最小的自然数k称为图G的选择数(或选色数),记为ch(G).

关于2-可选色的图,文献[2]作了特征化的论述.文献[3]证明了每个平面图是5-可选色的,且文献[4]证明了每个围长至少为5的平面图是3-可选择的.文献[5]构造了一个围长是4但不是3-可选择的图,因此要对3-可选择的平面图的特征还需进一步刻画,必须寻找一些条件,使得某一类平面图是3-可选择的.文献[6]论证了围长至少为4且无5-和6-圈的平面图是3-可选择的.文献[7-8]中论证了任何围长至少为4且无6-,8-和9-圈的平面图都是3-可选择的以及围长至少为4且无5-,8-和9-圈的平面图都是3-可选择的.
本文证明了每个围长至少为4且无8-,9-和10-圈的平面图是3-选择的.
2 基本引理
在证明定理之前,首先给出以下的三个引理:
引理2.1[9]若G是一个长度为偶数的圈,则G是2-可选择的.
引理2.2[7]若G是一个非-3-可选择图,且G的每一个非空真子集V∗⊂V的导出子图G[V∗]是3-可选择的,则G的任何一个长度为偶数的圈至少含有一个4+-顶点.
引理2.3[8]若G是一个非-3-可选择图,且G的每一个非空真子集V∗⊂V的导出子图G[V∗]是3-可选择的,若C1和C2是图中两个恰有一个公共顶点的4-圈,则C1和C2中至少有一个是non-minimal圈.
3 结论

由于考虑的图G不含长度为8-,9-和10-的圈,可得G具有下列性质:
(O1)一个4-面至多能和两个相邻的4-面相邻;
(O2)一个4-面不能和另一个6-面相邻;也不能和另一个7-面相邻;
(O3)一个5-面至多与两个4-面相邻;
(O4)一个5-面不能和另一个5-面相邻,也不能和另一个6-面或7-面相邻.
用权转移的方法调整所有的点和面的权值,调整后的权函数记为φ∗(x),若权的移动导致对所有的x∈V∪F,φ∗(x)≥0,则得到矛盾,从而完成定理的证明.当一个4-面f与i个4-面相邻时,称该4-面f为4i-面,其中i为0,1,2.权的移动根据以下规则:



图1 f是42-面时

图2 f是41-面时


由上述讨论,面f通过边uv转移的权值是小于或等于被调整后的定额数值,到这里证明了φ∗(f)≥0对于所有的x∈V∪F,所以有
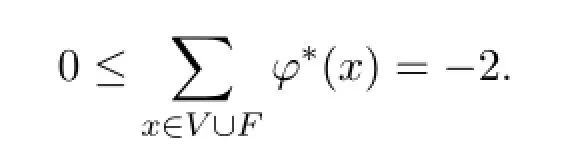
得出矛盾,得证.
[1]Bondy J A,Murty U S R.Graph Theory with Applications[M].New Youk:Macmillan Co.,1976.
[2]Erdos P,Rubin A L,Taylor H.Choosability in graphs[J].Congr.Numer.,1979,26:125-157.
[3]Thomassen C.Every planar graph is 5-choosable[J].Journal of Combinatorial Theory Ser.(B),1994,62(1): 180-181.
[4]Thomassen C.3-list-coloring planar graphs of girth 5[J].Journal of Combinatorial Theory Ser.(B),1995,64(1): 101-107.
[5]Voigt M.List colouring of planar graphs[J].Discrete Math.,1993,120:215-219.
[6]Peter C B Lam.The 3-choosability of plane graphs of girth 4[J].Discrete Math.,2005,294:297-301.
[7]张海辉,沈邦玉.关于无6-,8-和9-圈平面图的3-选色[J].南京师范大学报,2004,27:55-60.
[8]Zhang Haihui.On 3-choosability of plane graphs without 5-,8-and 9-cycles[J].Journal of Lanzhou University: Natural Sciences,2005,41:93-97.
[9]Alon N,Tarsi M.Colorings and orientations of graphs[J].Combinatorica,1992,12:125-134.
The 3-choosability of plane graphs without 8-,9-and 10-cycles
Zhu Xiaoying
(College of Jincheng,Nanjing University of Aeronautics and Astronautics,Nanjing211156,China)
An important researth on coloring of planar graphs is to determine whether a given planar graphs is 3-choosable or 4-choosable.In this paper,we study the choice number of special planers with girth at least 4. According to the discharging method,it is shown that every planar graph with girth at least 4 and without 8-, 9-and 10-cycles is 3-choosable.
choosability,plane graph,girth
O157.5
A
1008-5513(2013)06-0609-06
10.3969/j.issn.1008-5513.2013.06.009
2013-07-17.
朱晓颖(1979-),硕士,讲师,研究方向:图论及其应用.
2010 MSC:05C78

