单调压缩部分变换半群的秩
高荣海
(贵州师范大学 a.学报编辑部;b.数学与计算机科学学院,贵州 贵阳 550001)
在半群代数理论中,对于半群的秩或者幂等元秩是半群研究的一个热点内容之一,关于变换半群秩的研究已有许多成果[1-9].设S是一个有限半群,则S的秩定义为:rank(S)=min{|A|:A⊆S,A=S}.如果S是由幂等元集E生成,那么S的幂等元秩定义为:rank(S)=min{|A|:A⊆E,A=S}.1987年,文献[4]考虑了Xn上的奇异变换半群的秩,得到了它的秩为n(n-1)/2;1992年文献[5]证明了Xn上的保序奇异变换半群On和POn的秩分别为n和2n-1;2010年文献[6]引入保序压缩奇异变换半群,得到了它的秩为n-1,2011年文献[7]将文献[6]的结果进行推广,得到其理想的秩.在本文中,我们将单调性与压缩性引入到部分变换半群中,考虑了一类新的半群-单调压缩部分变换半群.设Xn={1,2,...,n}(n>4)并赋予自然序,Pn是Xn上的部分变换半群.设α∈ Pn,若对任意x,y∈domα⊆Xn,x≤y⇒ xα≤yα,则称α是单调递增的;若对任意x,y∈domα⊆Xn,x≤y⇒xα≥yα,则称α是单调递减的. 设α∈Pn,若对任意x,y∈domα⊆Xn,有|xα-yα|≤|x-y|,则称α是Pn的压缩元. 记MCPn为Pn中所有单调(递增或递减)压缩元构成的集合,易见MCPn在映射的合成下构成Pn的一个子半群.我们称之为Xn上的单调压缩部分变换半群.在这篇文章中我们得到了MCPn的秩为2n-1.
1 准备
设A,B是Xn的两个非空子集,若maxA 当α单调递增时,由单调性和压缩性容易验证α有如下表示法(称为α的标准表示): 这里,a1 当α单调递减时,由单调性和压缩性容易验证α有如下表示法(称为α的标准表示): 这里,a1>a2>…>ar,Ai 为 了 叙 述上的方便,对任意 α,β ∈MCP,定义 (α,β)∈ LΔ⇔ im(α)=im(β),(α,β)∈ RΔ⇔ ker(α)=ker(β), n(α,β)∈ JΔ⇔ |im(α)|=|im(β)|,则 LΔ,RΔ,JΔ都是 MCPn上的等价关系,易见 LΔ⊆JΔ,RΔ⊆JΔ. 对 0≤r≤ n-1,记JΔr={α∈MCPn:|im(α)|=r},则恰好是 MCPn的 n个 JΔ-类,其中是有空变换构成,并且 设 则顶端 JΔ-类有 2n-1 个 RΔ-类 RΔ(1,2),RΔ(2,3),...,RΔ(n-1,n),RΔ(1),...,RΔ(n)以 及 n 个 LΔ-类LΔ(1),...,LΔ(n). 本文的主要结果: 定理设自然数n≥4,则rankMCPn=2n-1. 在证明该定理之前,先给出下面几个相关的引理和推论. 引理1对任意α,β∈MCPn,若(α,β),(α,αβ)∈ JΔ,则(α,αβ)∈ RΔ,(αβ,β)∈ LΔ. 证明该定理的证明较容易,可参见文献[6-7]引理1的证明. 由引理1知MCPn的任意一个生成集都必须覆盖中每 RΔ-类和每个 LΔ-类,而 JnΔ-1中共有2n-1个RΔ-类和n个LΔ-类.于是我们可得到下面的推论1. 推论1设自然数n≥4,则rankMCPn≥2n-1. 引理2对 0≤r≤n-2,有 证明在这里分0≤r≤1和2≤r≤n-2来加以讨论.由于对前一种情形相对容易验证,所以在这里仅讨论后一种一般的情形. 情形1|bi+1-bi|=1(i=1,2,…,r-1),且|Ai|=1(i=1,2,…,r),不妨设Ai={ai},下面分两种子情形讨论: 情形1.1若ai+1=ai+1(i=1,2,…,r-1),由于 r≤n-2可知,要么 a1≠1要么 ar≠n,不妨设a1≠1. 当α单调递增时: 1)若b1≠1,令则有β,γ∈ JΔr+1,且α=βγ. 2)若b1=1,令 则有β,γ∈ JΔr+1,且α=βγ. 当α单调递减时: 1)若b1≠n,则β与单调递增1)中的相同,在γ中,只需将b1-1改为b1+1; 2)若b1=n,则β与单调递增2)中的相同,在γ中,只需将br+1改为br-1,则有β,γ∈ JΔr+1且α=βγ. 情形1.2若有某个i(2≤i≤r),使得ai-ai-1>1 当α单调递减时: 1)若b1≠n,令则有β,γ∈ JΔr+1,且α=βγ. 2)若b1=n则有β,γ∈ JΔr+1,且α=βγ. 若α单调递增时: 1)若b1≠1,则β与单调递减时的1)中的β相同,γ只需将单调递减时1)的b1+1改为b1-1即可; 2)若b1=1,则β与单调递减时的2)中的β相同,γ只需将单调递减时2)的br-1改为br+1即可. 情形2|bi-bi-1|=1(i=2,…r),且有某个 k(1≤k≤r),使得Ak>1,设x=minAk. 当α单调递减时: 1)若 b1≠n,令 2)若b1=n,令 则有β,γ∈ JΔr+1,且α=βγ. 当α递增时,可仿照情形1.2的方式进行讨论即可. 情形3若存在某个j(2≤j≤r),使得|bj-bj-1|>1(j=2,…r),由于r 由引理2可得下面的推论2. 推论2设n≥4,则是MCPn的生成集,即MCPn=<>. 注1设ei(i=1,2,…,n)是Xn{i}上的恒等变换,则根据MCPn中元素的标准表示知LΔ(i)={ei}(i≠1,n). 设集合S为 引理3设自然数n≥4,则JnΔ-1⊆ 证明由S中元素的特点知,S中的元素恰好覆盖了中的所有RΔ-类和LΔ-类.下面需证明JnΔ-1中的元素均可由S中的元素生成,即只需证明JnΔ-1S⊆ 对任意α∈JnΔ-1S,下面分4种情形讨论: 情形1α单调递增且α∈LΔ(1).此时,直接计算可知,为了后面讨论的方便,记该α为 情形2α单调递增且α∈ LΔ(n). 此时,一定有某个k,使得α∈ RΔ(k,k+1)(1≤k≤n-1). 或者α∈ RΔ(k)(1≤k≤n). 1)当α∈ RΔ(k,k+1),通过计算可得 (注:此处当k=1时,α↑k,1指的是情形1下生成的单调递增元素α,下同) 2)当α ∈ RΔ(k)且 k=1或者n时,通过计算可得;若k≠1,n时,计算可得 情形3α单调递减且α∈ LΔ(1). 此时,一定有某个k,使得α∈ RΔ(k,k+1)(1≤k≤n-1). 或者α∈ RΔ(k)(1≤k≤n). 1)当α∈ RΔ(k,k+1),通过计算可得 2)当α ∈ RΔ(k)且k=1或者n时,通过计算可得;若k≠1,n时 ,计算可得 情形4α单调递减且α∈LΔ(n),与情形2,3讨论相似,若α∈RΔ(k,k+1)有;若α∈RΔ(k)且k=1或者n时,有 定理的证明由引理3与推论2,得MCPn= [1]Garba G U.On the idempotent ranks of certain semigroups of order-preserving transformations[J].Portugal Math,1994,51. [2]Barnes G,Levi I.On idempotent ranks of semigroups of partial transformations[J].Semigroup Forum,2005,70:81-96. [3]Umar A.On the ranks of certain finite semigroups of order-decreasing transformations[J].Portugal Math,1996,53:23-34. [4]Gomes G M S,Howie J M.On the rank of certain finite semigroups of transformations[J].Math Proc Camb Phil Soc,1987,102. [5]Gomes G M S,Howie J M.On the ranks of certain semigroups of order-preserving transformations[J].Semigroup Forum,1992,45:272-282. [6]徐波,冯荣权,高荣海.一类变换半群的秩[J].数学的实践与认识,2010,40(8):222-224. [7]高荣海,徐波.关于保序压缩奇异变换半群的秩[J].山东大学学报:理学版,2011,46(6):4-7. [8]高荣海,徐波.降序严格部分变换半群的幂等元秩[J].河南师范大学学报:自然科学版,2010,38(6):4-7. [9]高荣海,徐波.降序有限部分变换半群的幂等元秩[J].西南大学学报:自然科学版,2008,30(8):9-12.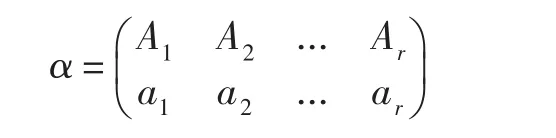
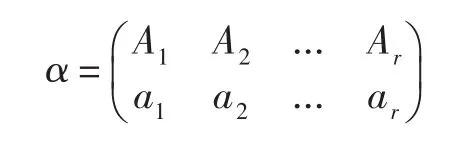
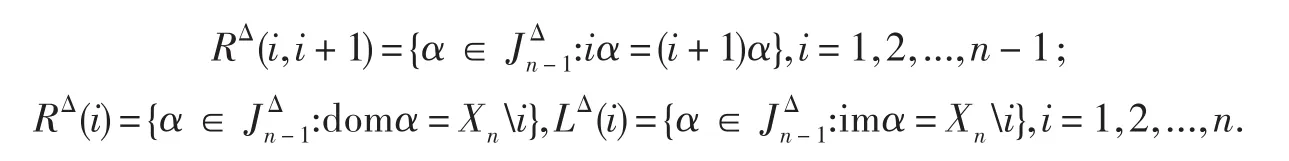
2 主要结果及证明

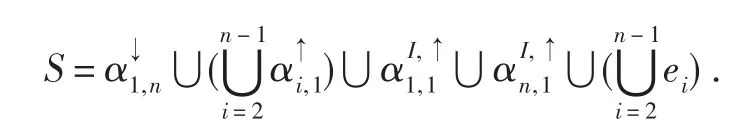
..,其中S如前定义.注意到,|S|=2n-1,所以rank(MCPn)≤2n-1. 结合推论1,即证得rank(MCPn)=2n-1.

