非磁性掺杂下石墨烯纳米带的自旋输运

蒋 超，王雪峰，翟明星，陈安邦，刘玉申

（1.苏州大学 物理科学与技术学院，江苏 苏州 215006；2.江苏省新型功能材料重点建设实验室，江苏 常熟 215500）

1 引言

石墨烯，即单原子层的石墨，自从2004年发现以来[1]，便引起了人们广泛的注意，被认为是理想的纳米电路材料.然而完美的石墨烯是零隙半导体，在制造器件中有一定的局限性.因而为石墨烯能带开启带隙成为一个非常重要的课题.一维尺寸受限的石墨烯纳米带（Graphene Nanoribbons，GNRs）因其可变的带隙而受到关注[2-4].按照其边界的不同形状，GNRs可以分为扶手椅型 GNRs（AGNRs）和锯齿型GNRs（ZGNRs）.不同宽度的AGNRs可以表现出金属或者半导体性质，而ZGNRs则是有带隙的反铁磁半导体，其边缘态存在局域磁性[4-5].GNRs的这些特殊物理性质被认为在未来的自旋量子电子学中有实际应用前景.

GNRs，特别是ZGNRs，在设计制造量子器件和纳米电子器件中显示出了很大的潜力[6-7].但是在大多数情况下，完美的ZGNRs表现出了自旋简并且整体无磁性.这在一定程度上会抑制其在自旋电子器件中的应用，所以我们需要找到一种途径来使自旋退简并.掺杂能给系统引入电子或者空穴[8]，并改变系统的能带结构，是人们调制GNRs电子性质的一种极其有效的方法.如果在纳米带边界掺杂，一边的自旋极化将会受到很大的抑制并使纳米带整体出现磁性[9].Gorjizadeh等人通过第一性原理研究了石墨纳米带掺入不同杂质原子时的电子结构，他们发现掺杂一些过渡金属，纳米带结构会更稳定，而且体系会伴有很高的自旋极化率[10].Zheng XH等人研究了掺杂硼（B）原子和氮（N）原子后的ZGNRs的输运性质，以及其中束缚态和准束缚态的出现[11].Ren H等计算了掺杂N原子扶手椅型纳米带的I-V曲线，发现了负微分电阻现象[12].Zhang HD等人报道了在特定位置掺杂的AGNRs，其正偏压和负偏压下都会表现出很大的负微分电阻[13].NDR效应是实现许多电子器件包括高频振荡器、频率倍增器、存储器和快速开关等的一个重要机制，在GNRs中获得这个效应很有应用价值[14].最近，Wu TT等发现在掺杂铍（Be）原子的ZGNRs中观察到了自旋NDR现象[15].总的来说，目前对NDR效应自旋依赖性的报道并不多，继续进行相关研究很有必要.

本文将对铝（Al）和磷（P）原子边界替代掺杂后的ZGNRs中的自旋输运特性进行研究.在偶数个原子宽度的Al原子掺杂的ZGNRs的I-V特性曲线中，我们发现仅仅在单自旋流出现NDR效应，在另外一个方向的单自旋流并没有出现这个现象.但是对于P原子掺杂的情况，这种单自旋流的NDR效应并不明显.通过进一步研究其透射谱发现，替换边缘C原子的Al（P）原子为施主（受主）杂质，它一方面使透射谱自旋发生极化，另一方面在杂质态能量处引入透射低谷.在1 V左右的偏压区域，输运能量窗口内下自旋透射谱随偏压分别呈快（慢）的下降趋势，并导致I-V曲线分别出现NDR（饱和）现象.

2 建模与方法

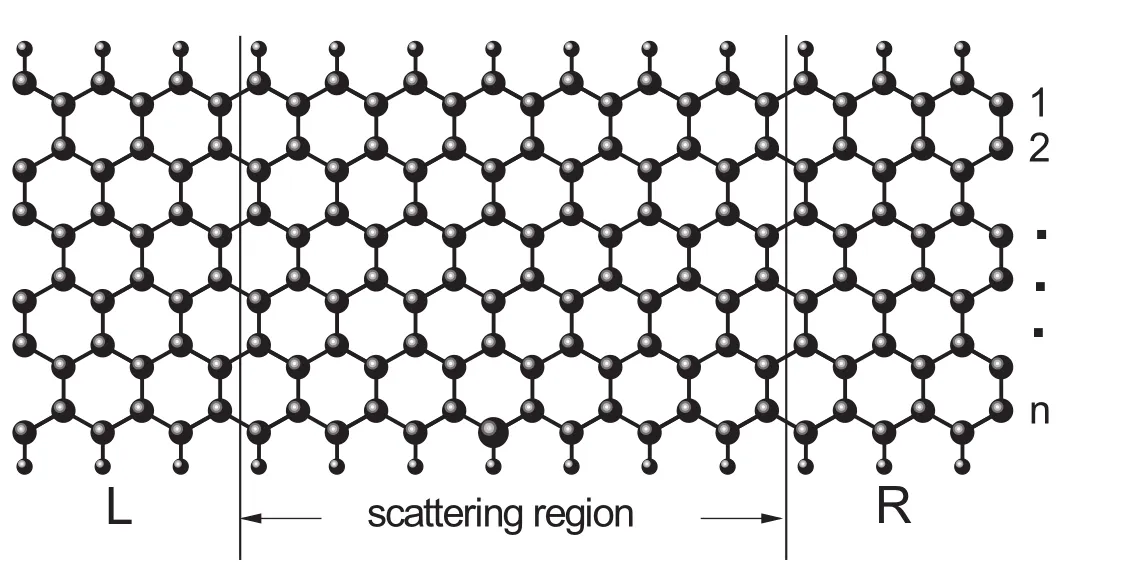
图1 锯齿形边界石墨烯纳米条带简图，包含左（L）右（R）电极，中间散射区.下边界较大原子代表掺杂原子，数字n表示条带的宽度

为了模拟ZGNRs并计算其电流电压（I-V）特性，我们设计了一个如图1所示的器件系统.对于n个原子宽度的ZGNRs器件，系统包含三部分：半无限长左电极（L），中间散射区，半无限长右电极（R）.边界碳（C）原子用氢（H）原子饱和.中间散射区中间的碳原子用其他原子替代掺杂，掺杂原子包括Al和P原子.

使用基于密度泛涵理论和自洽非平衡格林函数的Atomistix toolkit（ATK）软件包[16-17]对器件系统中的电子输运过程进行计算模拟.交换关联势采用局域密度近似（Local Density Approxima⁃tion，LDA），基组采用SZP（SingleZetaPolarization）.系统结构的优化采用准牛顿方法，精度设为0.05 eV/Ang.简约布里渊区K点数设为1×1×100，为避免超胞镜像间相互作用，真空层取15埃，能量截断半径取150 Ry以达到计算效率和精度的平衡，电子温度为室温300 K.

在系统两极之间施加偏压Vb并计算出系统的伏安特性曲线.透射系数由以下公式[18]计算得到：

其中，GC是中间区的格林函数，ΓL/R代表左右电极的耦合矩阵.电流值由Landauer-Büttiker公式[19]计算得到：

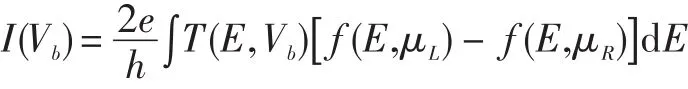
其中，E为电子能量，f（E,μL/R）是左/右电极中电子在非平衡状态下的费米分布. μL=μ0+eVb/2，μR=μ0-eVb/2，分别为左右电极化学势.本工作选取Vb的范围为0 V到1.6 V.

3 结果与讨论

当在边界上掺入杂质，ZGNRs的自旋简并将会被打破.上自旋电流和下自旋电流呈现强烈的自旋独立性，而且变化趋势表现出明显的不同.计算结果显示，在电流电压（I-V）特性曲线中，不同宽度的ZGNRs都有不同的阈值电压，从3-ZGNRs的0.4 V减少到8-ZGNRs的0.3 V.当偏压高于阈值电压时，左电极中价带电子通过散射区到达右电极.随着偏压增大，两电极能带间的能量交叠区间增大，电流值开始逐渐增大.

图2 掺杂Al和P原子的n-ZGNRs的电流电压（I-V）特性曲线.（a）和（b）分别是Al和P掺杂的结果.n代表ZGNRs的原子宽度，在这里分别是3、4、5、6、7和8.实线和虚线分别代表上自旋和下自旋电流

图2为不同宽度的掺杂Al和P原子的ZGNRs的I-V特性曲线.对于Al掺杂的3-ZGNRs来说，不论是上自旋还是下自旋电流，在阈值电压以上，除了在0.5 V～0.6 V之间有一个小的负增长，都会随着偏压的增加而增加.在P掺杂的3-ZGNRs中也有类似的现象发生.但是，在4-ZGNRs中却出现了不一样的现象.在Al掺杂的4-ZGNRs中，上自旋电流随着偏压的增加而增加；而下自旋电流在0.8 V左右的时候达到一个峰值，在[0.8，1.1]V范围内，电流值随着偏压的增加而减小.即在此区间，下自旋电流出现了负微分电阻（NDR）效应.当偏压大于1.1 V电流又恢复了增长的态势.在P掺杂的4-ZGNRs中，上自旋和下自旋电流随着偏压的增加而增长，但是在偏压增加到0.8 V左右时，不论是上自旋还是下自旋电流将会达到饱和，电流随着偏压的增加会保持不变或者变化很小.

经过对比研究发现，掺杂同种类型（P型或N型）原子的同种类型宽度（偶数或奇数个原子宽度），系统的I-V曲线具有相同的变化趋势.具体的，在奇数原子宽度ZGNRs的I-V曲线中，不论是上自旋还是下自旋电流，在偏压很小的一个范围内会出现台阶或者稍微的减小，其他时候电流将随着偏压的增加而单调增加.对于P原子掺杂的偶数宽度系统，在电流随着偏压增加到一定值的时候，将会出现饱和，电流近似保持不变.在偶数宽度ZGNRs中掺杂Al原子时，上自旋电流单调增加，而下自旋电流在偏压增加到一定值的时候，将会出现负微分电阻效应.这个自旋负微分电阻现象在6-ZGNRs中表现最为明显.

另外我们发现，奇数宽度纳米带I-V曲线的下自旋电流大于上自旋电流，而偶数宽度的I-V曲线中的下自旋电流小于上自旋电流.这个现象对于两种类型掺杂的ZGNRs都是相同的，其原因是由纳米带的上下对称性所造成的[15].

为了理解在偶数个原子宽度下掺杂Al原子出现负微分电阻效应的内在物理机制，我们计算了零偏压下Al和P掺杂的6-ZGNRs的透射谱函数和相应的以中间散射区为超胞的周期系统能带图，如图3所示.相对于完美ZGNRs，掺杂无疑对ZGNRs的能带结构产生了一定的影响，从图3（a）和（b）中左侧的能带图可以看出，在费米能级附近的能带出现了自旋分裂，上自旋和下自旋不再简并；其次，在价带顶附近有两支下自旋能级，只有一支上自旋能级，同时，在导带底附近却有两支上自旋能级，只有一支下自旋能级.对比完美6-ZGNRs的能带结构图（这里我们未画出），我们发现，价带顶附近的一支上自旋能级和导带底附近的一支下自旋能带消失了.除此之外，掺杂Al的纳米带中，在能量-1.2 eV和1.2 eV处各出现上下自旋能带；而掺杂P时，则在能量-0.9 eV和1.2 eV处各出现上下自旋能带.这时石墨烯边缘的Al原子为施主杂质（n-型）而P原子为受主杂质（p-型）.

由于掺杂后在导带底部和价带顶部分别少了一条自旋下和自旋上能带，与未掺杂纳米带能带相比，透射系数在相应的能量上减少.同时，透射谱分别在新出现的与杂质有关的两组能带附近出现反共振低谷.类似的结果在Zheng XH等人的文章中也有报道[11].

除此之外，我们还计算了掺杂6-ZGNRs在不同偏压下的透射谱，如图4所示.在偏压0.3 V下，两个电极的带隙交叠，对于两种不同的自旋透射谱，一个较宽的带隙出现在[-0.35，0.35]eV的范围内.相比于零偏压下的透射谱，随偏压增加Al杂质态导致的透射谱谷向费米能级靠近，而与P杂质原子相对应的透射谱谷则远离费米能级.由于费米能级附近[-0.3/2，0.3/2]eV的传输窗口仍然落在透射带隙之中，因此电流仍然近似为零.

图3 零偏压下Al（a）和P（b）掺杂的6-ZGNRs的透射谱和相对应的中间散射区的能带结构对比.实线和虚线分别代表上自旋和下自旋电子

当偏压Vb＞0.4 V，两个电极的能带进一步上移和下移，以致于左电极价带顶的电子可以传输到右电极的导带底，此时器件呈现双极型晶体管特性.宽度为eVb-0.38 eV的透射窗口出现在传输窗口中，电流将随着这个透射窗口宽度的增大而增加.透射窗口内出现若干透射峰，峰的形状取决于左右电极和中间区的波函数的交叠积分.在Vb=0.6 V时，Al和P掺杂的6-ZGNRs在传输窗口中具有类似的透射窗口形状，而且具有相似的上自旋和下自旋值.

当偏压增加到0.8 V时，透射窗口进一步展宽，自旋效应已经比较明显.对于Al掺杂的情况，下自旋透射谱具有较高的值，而当偏压增长到[0.9，1.2]V时，下自旋的透射逐渐下降，而上自旋几乎没有变化，进而使得下自旋值逐渐小于上自旋值，在偏压[1.0，1.2]V范围内，上下自旋在透射窗口内将出现较大的峰（谷）值差距.而对于P掺杂的情况，上下自旋的电流随着偏压的增加一直呈现类似的情形，虽然下自旋值也有下降，但是并不像掺杂Al的情况那么快.这种下自旋值下降较快的现象在一定程度上解释了I-V曲线出现NDR效应的原因.随着偏压的进一步增加，费米能级附近的上下自旋值趋于一致，而且呈逐渐增加的趋势，I-V曲线又恢复单调递增趋势.

图4 不同偏压下的M-6-ZGNRs的透射谱.左右分别是Al-6-ZGNRs（a）和P-6-ZGNRs（b）. 这里主要选取0.3 V，0.6 V，0.8 V，1.0 V，1.2 V和1.5 V偏压下的图像.实线和虚线分别代表上自旋和下自旋电子.黑色水平线代表传输窗口，0.6V以上传输窗口内包含透射峰的区域定义为透射窗口.

4 结论

利用第一性原理系统地研究了边界替换掺杂的锯齿型石墨烯纳米条带的自旋输运性质.铝原子（Al）在边界为施主而磷原子（P）则为受主杂质.在掺杂Al原子的时候，上自旋电子和下自旋电子表现出不同的输运性质.在偶数个宽度的情况下，上自旋电子随电压的增长而增长，而下自旋电子电流在某个偏压区间内呈现出负微分电阻效应.通过计算中间散射区的能带和不同偏压下的透射谱发现，在负微分电阻发生的偏压区间，下自旋的透射谱的值将会随着偏压的增加下降很快，同时上自旋的值却变化很小.这些可以简要的用来说明负微分电阻发生的原因.

[1]Novoselov K S,Geim A K,Morozov S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306:666-669.

[2]Kobayashi Y,Fukui K I,Enoki T,et al.Edge state on hydrogen-terminated graphite edges investigated by scanning tunneling microscopy[J].Phys Rev B,2006,73:125415-1-8.

[3]Pisani L,Chan J A,Montanari B,et al.Electronic structure and magnetic properties of graphitic ribbons[J].Phys Rev B,2007,75:064418-1-9.

[4]Son Y W,Cohen M L,Louie S G.Energy Gaps in Graphene Nanoribbons[J].Phys Rev Lett,2006,97:216803-1-4.

[5]Nakada K,Fujita M,Dresselhaus G,et al.Edge state in graphene ribbons:Nanometer size effect and edge shape dependence[J].Phys Rev B,1996,54:17954-17961.

[6]Li Y F,Zhou Z,Shen P,et al.Spin Gapless Semiconductor-Metal-Half-Metal Properties in Nitrogen-Doped Zigzag Graphene Nanoribbons[J].ACS Nano,2009,3(7):1952-1958.

[7]Jaiswal N K,Svivastava P.Structural stability and electronic properties of Ni-doped armchair graphene nanoribbons[J].Solid State Communications,2011,151:1490-1495.

[8]Martins T B,Miwa R H.Electronic and Transport Properties of Boron-Doped Graphene Nanoribbons[J].Phys Rev Lett,2007,98:196803-1-4.

[9]Ouyang Y J,Sanvito S,Guo J.Effects of edge chemistry doping on graphene nanoribbon mobility[J].Surface Science,2011,605:1643-1648.

[10]Gorjizadeh N,Farajian A A,Esfarjani K,et al.Spin and band-gap engineering in doped graphene nanoribbons[J].Phys Rev B,2008,78:155427-1-6.

[11]Zheng X H,Rungger I,Zeng Z,et al.Effects induced by single and multiple dopants on the transport properties in zigzag-edged graphene nanoribbons[J].Phys Rev B,2009,80:235426-1-8.

[12]Ren H,Li Q X,Luo Y,et al.Graphene nanoribbon as a negative differential resistance device[J].Appl Phys Lett,2009,94:173110-1-3.

[13]Zhang D H,Yao K L,Gao G Y.The peculiar transport properties in pn junctions of doped graphene nanoribbons[J].Journal of Applied Physics,2011,110:013718-1-6.

[14]Wu Y,Farmer D B,Zhu W,et al.Three terminal graphene negative differential resistance devices[J].ACS Nano,2012,6:2610-2616.

[15]Wu T T,Wang X F,Zhai M X,et al.Negative differential spin conductance in doped zigzag graphene nanoribbons[J].Appl Phys Lett,2012,100:052112-1-4.

[16]Brandbyge M,Mozos J L,Ordejon P,et al.Density-functional method for nonequilibrium electron transport[J].Phys Rev B,2002,65:165401-1-17.

[17]Taylor J,Guo H,Wang J.Ab initio modeling of quantum transport properties of molecular electronic devices[J].Phys Rev B,2001,63:245407-1-13.

[18]Dutta S.Electronic Transport in Mesoscopic Systems[M].Cambridge:Cambridge University Press,1995.

[19]Büttiker M,Imry Y,Landauer R,et al.Generalized many-channel conductance formula with application to small rings[J].Phys Rev B,1985,31:6207-6215.