汽车轮胎与转鼓的滚动特性分析*

张绍国，高 峰，徐国艳，崔 莹

(北京航空航天大学交通科学与工程学院，北京 100191)

前言

滚动阻力是高性能汽车轮胎的重要认证指标之一，滚动阻力降低20%，可实现节油2% ～4%，若全球汽车都使用低滚动阻力轮胎，每年可节约450亿升柴油和150亿升汽油。目前世界各国都在采取措施促进低油耗轮胎的普及，欧盟和美国相关新法规都对轮胎滚动阻力指标提出分级要求，达不到检测标准的轮胎不能进入相关国家的市场[1－2]。

轮胎滚动阻力测试是大载荷下小分量的试验，对测试设备的精度要求相当严格，室外道路滚动阻力测试由于各工况参数的可控性差，难以形成规范的操作流程，测试精度较低[3]。平带式试验机可以模拟高速连续状态下的路面运动，但在轮胎大载荷高速运动状态下，不能满足路面所具有的刚度和平整度的要求，测试效果不太理想[4－5]。传统的轮胎滚动阻力测试主要在室内转鼓试验机上进行，以转鼓曲面代替路面，并不能真实地反映车辆在水平道路上的行驶状态。

目前国内外对轮胎滚动阻力预测模型和测试方法进行了大量研究，但与测试设备研发相关的文献较少[6－8]。本文中从检测设备的结构模型出发，分别建立了转鼓式和平带式轮胎滚动阻力动力学测试模型，模拟了不同转鼓曲率下轮胎的静载荷和滚动阻力特性，评价转鼓曲率对轮胎滚动阻力测试结果的影响。

1 设备结构分析

设备采用转鼓式结构，由于转鼓的起动转矩要比稳速转矩大得多，转矩计必须能承受大的转矩，并能精确地测量小的转矩，且测量必须在无加速转矩输入时进行，测试上难于实现，精度很难保证，故现在国外相关设备滚动阻力的计算均采用测力法，通过测量轮胎轴上的反作用力来实现[9]，设备主要结构如图1所示。

轮胎通过连接法兰安装在轮轴装置上，轮轴装置与传感器板通过螺栓固定在一起。驱动电机带动转鼓旋转，通过控制转鼓的转速可以测试不同速度下汽车轮胎滚动阻力的大小。径向加载系统通过传感器板给轮胎施加大小不同的载荷，并把轮胎紧紧压在转鼓的表面上，与转鼓相配合，可以模拟轮胎在各种工况下的运行情况。

旋转的轮胎与转鼓之间的接触压力使轮胎发生变形，产生滚动阻力矩，通过轮轴以反作用力形式传递给传感器板。合理布置传感器的安装位置，采集目标检测点的变形量，经过数据处理，求得不同工况下的轮胎滚动阻力。

平带式轮胎试验机结构见图2，通过垂直的径向激发器对轮胎施加不同的载荷，驱动装置带动不锈钢道路系统，进而驱动轮胎以不同速度旋转，路面支撑系统对不锈钢道路提供支撑。

2 计算模型的建立

ABAQUS是目前国际上较先进的有限元分析软件，本文中的测试模型在该软件的显式计算平台上完成。

2.1 轮胎有限元模型

轮胎以某成品子午胎11R22.5 16PR为研究对象。它主要由橡胶和帘线(钢丝帘线、绵纶帘线和聚酯帘线)等组成。橡胶作为超弹性材料，具有大变形和高弹性的力学特点，本构关系相当复杂，本文中采用Yeoh三次方程表征胶料的力学性能，即

式中:W为橡胶应变能函数;I1为第1应变不变量，由橡胶材料拉伸试验3个正交方向的变形率确定;C10、C20、C30为常数，由材料试验数据拟合确定。

轮胎的滚动阻力主要是由轮胎黏弹性引起的滞后损失造成，通过轮胎的变形，主要以内摩擦损失的形式表现出来，以热量形式散发出去，故在轮胎滚动阻力分析中要考虑热力耦合情况。

计算轮胎的温度场分布时，主要考虑胎体热源和轮胎内外表面与外界的热交换两个方面。胎体热源的计算式[10]为

式中:σp和εp分别为热源单元的应力和应变幅值;ω为轮胎稳态滚动角速度;tanδ为材料的损耗正切，可由动态模量仪测得。

根据轮胎温度场的分布情况和不同温度下轮胎材料对应的损耗正切值，将轮胎温度作为热应力施加给轮胎稳态滚动分析模型，计算不同工况下轮胎的滚动阻力。

2.2 求解方程

ABAQUS/Explicit采用非线性求解技术，可模拟复杂接触关系的显式动力学问题，但必须考虑结构加速度所引起的惯性力影响，结构的动力学平衡方程通用表达式[11]为

式中:M为质量矩阵;P为外力;K为刚度矩阵;C为阻尼矩阵;u为位移。

对于准静态结果，理想的情况是将加载时间增加到最低阶模态周期的10倍，模态特征方程的表达式为

式中:p为振动频率;Φ为频率对应的特征向量。

对其求解即可得到轮胎各阶频率和模态。根据计算结果，提取轮胎基频，选定稳态分析步长为0.1s。

2.3 边界条件

影响轮胎滚动阻力的因素很多，本文中主要从使用条件方面考虑载荷、充气压力和稳态速度对轮胎滚动阻力的影响，分析过程分为静载荷和稳态载荷2个步骤。

静载荷加载是在不滚动情况下对轮胎进行受力分析，包括轮胎气压和载荷两部分。稳态条件下，通过对转鼓或路面施加恒定的速度，驱动轮胎以设定速度做旋转运动。为使轮胎在轮轴上具有旋转自由度，须在轮辋和轮轴之间设置铰接属性，即两个连接点之间只能沿轮轴轴线方向发生相对转动。图3和图4分别为轮胎在稳态条件下的转鼓式和平带式结构的有限元计算模型。

3 静载荷分析

首先分析轮胎与水平路面静态接触受力情况。在垂向载荷逐渐增大的过程中，轮胎产生变形，与地面的接触面积也逐渐增大，在胎面区域产生一个与垂向载荷相平衡的接触反力，不同垂向载荷下轮胎接地区域应力分布如图5所示。

当垂向载荷为1kN时，轮胎接地区域的最大应力在接地区的中心部位，接地区的形状接近圆形，随着垂向载荷逐渐增大，最大应力向两侧胎肩方向扩展，形状逐渐变为椭圆形，接地区中心的应力与边缘相比增幅减小，高应力区逐渐向两侧胎肩处移动。当载荷为5kN时，接地区域形状类似矩形，在胎肩部位应力最大，接地区的应力变为中心低、边缘高，即发生翘曲现象。

图6为轮胎在20kN载荷下不同转鼓直径时的下沉量曲线。转鼓直径越大，轮胎中心位置下沉量越小，在转鼓直径较小时，该曲线的变化趋势较快，转鼓直径增加到2.0m以后，下沉量与转毂直径的变化趋势逐渐平缓，这与文献[12]的试验结果一致。

图7和图8分别为采用直径为1.0、2.0和4.0m的转鼓以及平带式时，轮胎静载荷工况下，接地区域法向应力沿纵轴(轮胎对称中面与地面的交线)和横轴(轮胎旋转轴线在地面的投影)的分布曲线，其中弧坐标原点为接地区域中心。

由图7可见，在额定载荷作用下，在纵轴方向，接地区域应力分布中心低、边缘高，即发生翘曲现象。转鼓直径较小时，轮胎接触应力比较大，中心区域相对比较平坦，翘曲现象不明显。随着转鼓直径增大，接触应力逐渐减小，翘曲也愈加明显;到平带时，翘曲最显著。

由图8可见，沿横轴方向，胎肩处的接地应力高于胎冠中心处，应力分布比纵轴方向更不均匀，胎肩部位的应力大，易导致该部位的形变增大，相对于其它部位，此处更易发生肩空、脱层等现象。

通过以上分析可知，在静载荷状态下，不同转鼓直径对轮胎接地特性影响较大。转鼓直径越大，模拟平直路面效果越好，在转鼓直径达到2.0m以上时，转鼓尺寸对轮胎与地面之间接触特性的影响显著减小，本文中将重点分析直径为2.0与4.0m的转鼓和平带式3种情况滚动阻力测试结果的差异。

4 稳态分析

4.1 滚动阻力测试中传感器的布置方案

首先在额定载荷下对轮胎滚动阻力进行仿真测试。图9为转鼓测试中在0.05和0.1s时刻由轮轴反力产生的传感器板上的应变云图。它直接反映轮轴反力处的变形量。由图可见，它们呈现非完全对称形态。

通过分析不同工况下传感器板滚动阻力方向位移场分布情况，采用4个灵敏度完全一致的传感器以测力板形式安装在一起，来保证测试结果的准确性和有效性。4个传感器分别安装在传感器板4个角的位置，如图10中D1、D2、D3和 D4所示。

4.2 数据处理

滚动摩擦的受力情况比较复杂，表现为两接触物体在接触区域法向力和力矩作用下产生相对运动趋势。在传感器安装位置区域与其中心节点之间建立分布式耦合关系，通过分解滚动阻力方向在中心节点位移场独立的坐标成分，经过模拟标定，计算传感器安装位置平均受力情况，分析轮胎大变形滚动接触问题。为了准确地测定和计算轮轴的反作用力，对采集的4个传感器检测点上与应变对应的变形量数据 Ds(s=1，2，3，4)进行和差处理:

由式(5)算得的D权且称之为轮轴反力变形量。图11为额定工况下转鼓式和平带式模型轮轴反力变形量D的时间历程。轮胎在加速区域(0～0.05s)变形量相对较大，主要是受加速度产生的惯性力影响，轮胎达到稳态转速以后，变形量趋于稳定。

轮胎在转鼓的驱动下，在0.05s后转速稳定，采集0.07～0.1s区间的数据作为稳态测试数据，通过平均滤波，取算术平均值作为每种工况对应的轮轴反力变形U，即

式中:m为分析步数，Dj为分析步对应的变形量。

式(6)的计算结果是变形量，需要与力进行计量单位换算，故须对测试模型进行相应标定。在静载荷状态下，在轮辋参考点沿滚动阻力方向施加不同载荷，同时采集传感器检测点对应的变形量，把采集结果作为样本数据，依据最小二乘法对样本数据进行回归分析，得到变形量u和轮轴反力Ft的拟合方程为

式中k、b为回归系数。

在反力的单位为N，变形量的单位为mm的条件下计算求出k=1 807.62，b=27.11。

5 滚动阻力趋势性试验

11R22.5子午线轮胎的使用参数分别为:额定充气压力830kPa，额定载荷30.89kN，速度80km/h。首先在不同转鼓直径测试模型上分别在变速度、变载荷和变气压的条件下进行轮轴反力变形的仿真测试，结果如表1～表3所示。

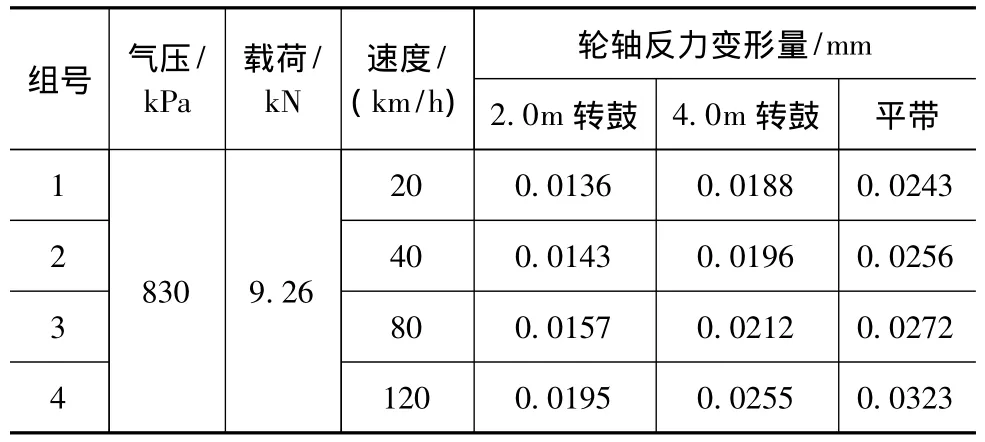
表1 变速度条件下轮轴反力变形量

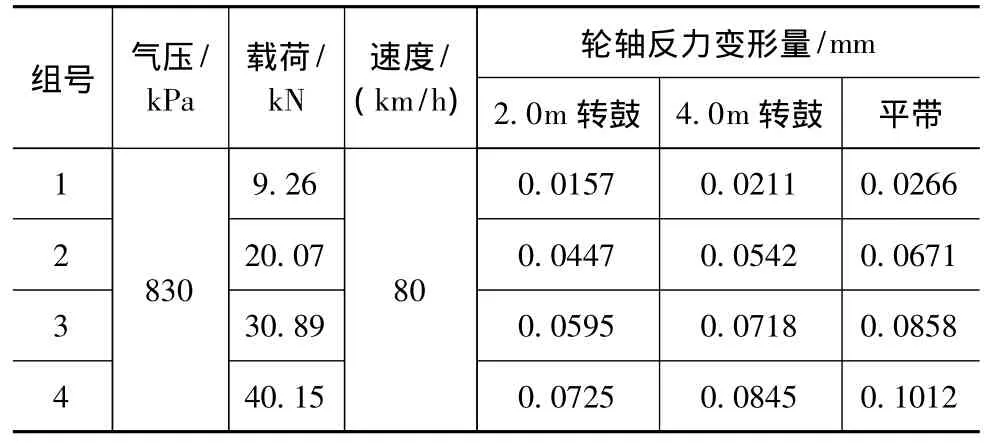
表2 变载荷条件下轮轴反力变形量

表3 变气压条件下轮轴反力变形量

由表中测试结果按式(7)算得轮胎旋转时轮轴上的反力，该力与轮胎滚动阻力的关系为

式中:Fr为轮胎滚动阻力;Ft为轮轴反力;L为轮轴中心到与转鼓接触面的距离;R为转鼓半径，对于平带模型，Fr=Ft。

依据 GB/T 18861—2002《汽车轮胎滚动阻力试验方法》，在 MTS公司的转鼓式轮胎滚动阻力试验机上进行相应工况下滚动阻力实测试验，设备转鼓直径为 1.7m，如图 12所示。实测数据及其与前面的仿真测试结果的对比如图13～图15所示。

图13为在额定气压和载荷工况下，滚动阻力与速度的关系曲线。由图可见，滚动阻力随速度增加而稍有提高，在高速区域变化相对较大，仿真测试结果与试验数据的变化趋势相符合。从数值上说，仿真测试值都比试验值大，相对而言，平带式的数据与试验值比较接近，随着转鼓直径的减小，误差增大。根据仿真测试结果，2.0m转鼓的滚动阻力比4.0m转鼓的最大高出4.9%;比平带最大高出14.7%。

图14为额定气压和速度工况下滚动阻力与载荷的变化关系，由图可见，载荷在20kN以下时轮胎滚动阻力几乎随载荷成正比增长。主要因为载荷的增大使轮胎变形更加明显，轮胎的内摩擦滚动阻力也相应增大;载荷在20kN以上时，滚动阻力随载荷而增长的趋势变缓。仿真结果和试验数据的变化趋势一致;数值上的对比情况与图13相似。仿真测试结果:2.0m转鼓的滚动阻力比4.0m转鼓最大高出6.7%;比平带最大高出18.1%。

图15为额定载荷和速度工况下滚动阻力与轮胎气压的变化关系，由图可见，滚动阻力随气压变大而减小，主要原因是充气气压升高使轮胎的胎体帘线张紧，刚度增大，在相同的载荷下下沉量下降，导致滚动阻力减小[13]。仿真结果和试验数据的变化趋势相符;数值上的对比情况与图13和图14类似。仿真测试结果:2.0m转鼓的滚动阻力比4.0m转鼓最大高出5.4%，比平带最大高出17.2%。

上述几种工况下滚动阻力仿真结果和试验数据的对比表明，计算值与试验数据的变化趋势完全吻合，说明本文的测试模型是合理和可靠的。2.0m转鼓仿真结果比试验数据最大高出25%左右，主要是因为难以构建精确的轮胎有限元模型，并且为节约计算成本，将轮轴、转鼓等作为刚体处理。

通过比较不同转鼓尺寸的计算结果可知，转鼓尺寸对轮胎的滚动阻力测试值有一定的影响，转鼓直径越大，滚动阻力测试值越小。在ISO28580和SAEJ1270中分别给出了不同转鼓直径的校正公式和转鼓平面近似公式。

式中:R1、R2为转鼓1和2的半径;r为轮胎名义半径;FR1为转鼓1测量的滚动阻力值;FR2为转鼓2测量的滚动阻力值。

式中:R为转鼓半径;FR为平面上的滚动阻力值;FW为转鼓上的滚动阻力值。

本文的结论与上述公式表征的变化趋势一致。根据上述仿真测试结果，不同工况下，2.0m转鼓的滚动阻力比4.0m转鼓最大高出6.7%;比平带最大高出18.1%。从生产成本和转鼓转动稳定性等因素考虑，测试设备选用2.0m直径的转鼓是合理的。

6 结论

(1)在标准气压和载荷下，转鼓直径越大，轮胎中心位置下沉量越小，转鼓直径增加到2.0m后，下沉量随转鼓尺寸变化的趋势逐渐平缓。

(2)不同转鼓直径对轮胎接地区域纵向和横向应力分布影响较大，转鼓直径越大，模拟平直路面的效果越好。

(3)仿真测试结果表明，滚动阻力随转鼓直径的减小而提高。不同工况下，2.0m转鼓的滚动阻力比4.0m转鼓最大高出6.7%;比平带最大高出18.1%。从成本角度和转动稳定性考虑，设备选用2.0m直径的转鼓是合理的。

[1]Jerome B，Jason B．Reducing Tire Rolling Resistance to Save Fuel and Lower Emissions[J]．SAE International Journal of Passenger Cars-Mechanical Systems，2009，1(1):9 －17．

[2]Anon．Tires and Passenger Vehicle Fuel Economy[J]．Transportation Research Board-Special Report，2006，286:1 －10．

[3]叶进雄．全钢载重子午胎滚动阻力有限元仿真与试验分析[D]．北京:清华大学，2007:7 －8．

[4]Ortiz A，Cabrera J A，Castillo J，et al．Analysis and Evaluation of a Tyre Model Through Test Data Obtained Using the IMMa Tyre Test Bench[J]．Vehicle System Dynamics，2005，43:241 －252．

[5]Cheli F，Braghin F，Brusarosco M，et al．Design and Testing of an Innovative Measurement Device for Tyreroad Contact Forces[J]．Mechanical Systems and Signal Processing，2011，25(6):1956 －1972．

[6]任礼行，刘清，张艾谦，等．轮胎滚动阻力测量与分析[J]．汽车工程，2000，22(5):316 －319．

[7]Miege A J P，Popov A A．Truck Tyre Modeling for Rolling Resistance Calculations Under a Dynamic Vertical Load[J]．Automotive Engineering，2005，219:441 －456．

[8]Shida Z，Koishi M，Kogure T，et al．Rolling Resistance Simulation of Tires Using Static Finite Element Snalysis[J]．Tire Science and Technology，1999，27(2):84 －105．

[9]韩秀芝．子午线轮胎稳态滚动阻力及水滑特性的研究[D]．北京:北京化工大学，2009:7－10．

[10]龚科家，危银涛，叶进雄．基于热力学有限元分析的轮胎滚动阻力仿真[J]．中国机械工程，2009:20(5):626－629．

[11]张文元．ABAQUS动力学有限元分析指南[M]．北京:中国图书出版社，2005:3－6．

[12]苗常青，田振辉，杜星文．轮胎与转鼓之间接触界面特性研究[J]．哈尔滨工业大学学报，2001，34(4):516 －519．

[13]庄继德．汽车轮胎学[M]．北京:北京理工大学出版社，1995:180－183．