一种开域静磁场双标量位混合有限元边界元法研究

王占辉 ，高俊吉

（1. 海军后勤部后勤办，北京 100841；2. 海军工程大学，武汉 430033）

0 引言

电磁场开域问题是电气工程与电磁散射和辐射领域中常遇到的一类问题。有限元法目前在电磁场分析计算中居主导地位，但从原理而言，它不适于解决开域问题。边界元法可以解决开域问题，但处理非线性问题及多种介质问题比较困难。如果在铁磁区采用有限元进行离散，而在铁磁边界上采用边界元法进行离散，然后把两种方法在边界上有机结合起来，即可完成对无界域的求解。这就是有限元－边界元混合方法。该方法综合了有限元法与边界元法的优点，成为目前解决复杂开域问题最有效且最受人们重视的方法之一。

应用混合有限元边界元法来求解开域问题的基本思想[1]就是将整个求解区域（即无限空间）划分为有限元区域与边界元区域，有限元区域含源，含多种线性或非线性介质；边界元区域则为外部的无限自由空间。在有限元区域内采用有限单元剖分。对于两区域的相交边界采用边界单元剖分。最后通过两区域相交边界上的交界条件，将有限元方程与边界元方程结合起来，得到“混合方程”。求解混合方程确定两区域相交边界上的信息后，即可确定边界元区域即外部无限自由空间中任一点的磁位值或磁场值。

本文对全标量位与部分标量位相结合的双标量位混合有限元边界元法进行了研究及仿真计算，计算结果表明了该方法的正确性及高精度。

1 双标量位的定义[2]

图1所示为开域静磁场问题，区域A为铁磁区域（区域内不存在传导电流），B为电流区域（磁导率μ=μ0为常数），C为导体及空气区。区域A和区域C两种介质的交界面为Γjk。

图1 开域静磁场示意图

1.1 全标量位

无电流的铁磁区域A为无旋场，其场强可以用一个标量位的负梯度表示，则存在全标量磁位设为ψ，使H=-ψ▽ ，其中ψ称为全标量位，它可以用来表征磁场中总的场强[3]。

利用全标量位，则磁感应强度可以表示为

当磁场区域存在铁磁介质时，上式为非线性拉普拉斯方程，它描述了静磁场中不存在电流区域的情况。

1.2 部分标量位

一般情况下可以认为空间任何一点的实际磁场是由电流源部分所产生的磁场和物质被磁化所产生的磁场两部分的叠加，即（式中为空间任意点的磁场强度；为由宏观传导电流在真空介质中产生的磁场强度；为铁磁介质被磁化后分子电流磁矩产生的磁场强度）。

对于电流J产生的磁场强度有；由于，因此，磁化强度的旋度为零，即

则为一无旋场，可以用一个标量位φ的负梯度来表示，即；标量位φ部分地描述了磁场的性质，它的负梯度表征了磁化部分的场强，因此称为部分标量位。

采用部分标量位方法，显然在计算中带来不少方便，由于每一个节点只有一个未知量，大大降低了对内存的要求。

在有电流的区域B中，采用部分标量位设为φ，其方程为

2 有限元公式

将铁磁区域A进行剖分，解函数ψ用基函数Ni和节点函数值ψi展开，即（其中，n为求解区域中的节点总数）

3 边界元公式

对于有电流的区域B中的磁场微分方程(2)，其二维问题的格林函数为；三维问题的格林函数为；r是源点到场点的距离。

则通过加权余量法可以得出区域B的边界积分方程为[4]

二维情况t=θ2π，θ为点i所张平面角；

三维情况t=Ω/4π，Ω为点i所张立体角。

将交界面为Γjk剖分成有限数量的单元。将解函数φ（∂φ/n∂）用基函数和节点函数值iφ展开，即（其中，k为单元的插值节点数）。这里插值基函数的选取可采用线性单元，也可用常单元。

本文中φ的基函数采用一次线性单元，∂φ/∂n的基函数采用常单元。方程离散为

4 混合方程

4.1 交界面条件的处理

由电磁学[3]的知识可知，在两种不同介质的交界面上，磁感应强度的切向分量是连续的，如果交界面上不存在面电流，则磁场强度的切向分量也是连续的，即

其中，下标j，k表示两种不同的介质；n表示法向分量；t表示切向分量。

由于在铁磁区域A中，任一点磁场强度H=-▽ψ，而在电流的区域B中H=-▽φ+Hs；（其中Hs为电流产生的磁场），则在两区域的交界面Γjk上，根据方程(7)，可以得到

从而可以导出磁位交界面条件。

这里的全标量位ψ的零点选在坐标原点上，部分标量位φ的零点选在无穷远处。假设地磁场为均匀场，设地磁场向量为则在边界上任一点A(xi,yi,zi)处，坐标原点到该点的向量，则地磁场在A点的标量磁位可以直接求出，为

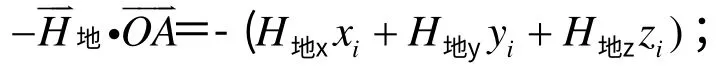
由于边界上任一点的全标量位与部分标量位之差即为地磁场在该点产生的标量磁位，则直接可以得到边界点A处的全标量位与部分标量位的关系:

综上，交界面的条件为

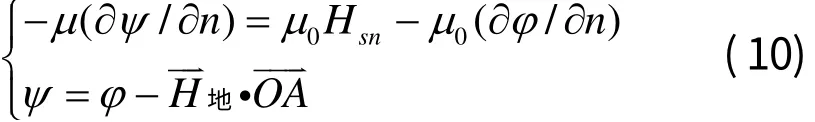
4.2 形成有限元－边界元混合方程

对交界面条件进行处理后，联立有限元边界元方程，结合交界面条件(10)可以得到有限元－边界元混合方程如下：

解之即可得到边界Γjk上离散点处的φ、∂φ/∂n；以及区域A中的ψ。利用求得的边界Γjk上的φ、∂φ/∂n即可求得空间中任一点的磁场。

5 仿真算例

对地磁场中各向同性的铁质均匀无限长空心圆柱体进行了仿真计算。

尺寸－外径：2 m；内径：1 m。地磁场纵向分量27.85（A/m）；横向、垂向分量为零；圆柱体相对磁导率：100。

取空心圆柱体的任意一个与中轴垂直的截面，将其剖分成48个三角形单元，36个节点。

环外计算点－纵向：-4~4 m；横向：5 m；

环内计算点－纵向：-0.5~0.5 m；横向：0.6 m。

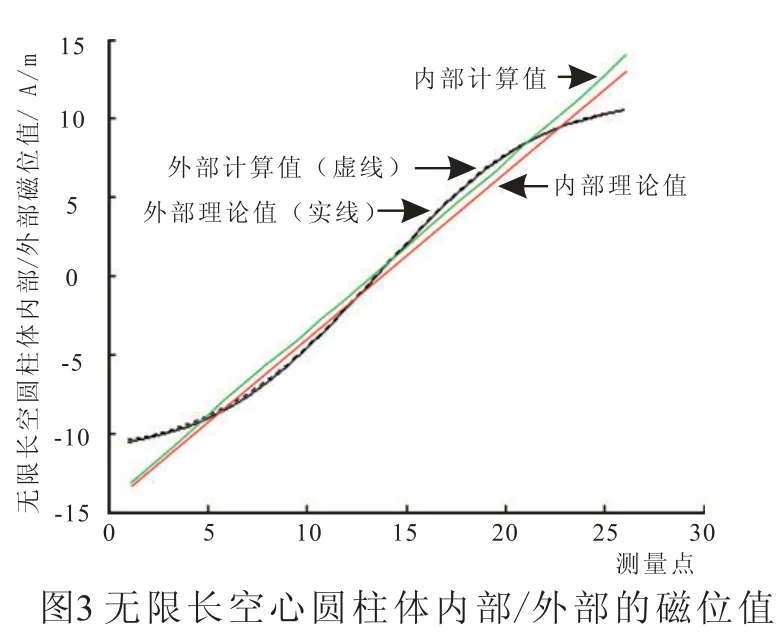
计算结果见图2～图3。

计算误差－铁区误差：1.03%；内部误差：7.02%；外部误差：1.23%。（最大值误差[5]）

从仿真结果可以看出，计算结果比较准确，说明该算法对开域静磁场问题有较好的适用性。

图2 无限长空心圆柱体铁区中的磁位值

6 结束语

本文对开域静磁场的双标量位混合有限元边界元方法进行了研究。在该方法中，在铁磁区域采用全标量磁位，而在电流区和自由空间采用部分标量磁位。通过对交界面条件的处理，导出全标量磁位与部分标量磁位在自由空间和铁磁区交界面的耦合边界条件。进而推导出双标量位混合有限元与边界元耦合算法。仿真计算说明本方法对开域静磁场问题有较好的适用性。

混合有限元边界元方法的主要缺点是所得到的代数方程组的系数矩阵不再对称且不定，系数矩阵的条件数易变得较大，病态较严重，这使得求解比较困难。这就需要采用预条件双共轭梯度法等求解方法进行处理。这是提高该方法计算效率的有效途径之一。

[1] S.J.Salon. The hybrid finite element-boundary element method in electromagnetics, IEEE Transac- tions on Magnetics.Vo1.Mag.21, No.5, September, 1986,1829～ 1834.

[2] 颜威利, 杨庆新, 汪友华等.电气工程电磁场数值分析.北京：机械工业出版社,2005：110～115.

[3] 冯慈璋. 电磁场.北京：高等教育出版社,1983：134-138.

[4] 倪光正,杨仕友,钱秀英等.工程电磁场数值计算.北京：机械工业出版社, 2004：237～242.

[5] 周耀忠,宋武昌,唐申生.潜艇磁场外推的数学模型研究. 海军工程大学学报, 2003, 15(4)：31～35.