平行导线磁场对点阵式霍尔电流传感器测量准确度的影响分析
许进宝,戚连锁,庄劲武,李思光
(海军工程大学电气工程学院,武汉 430033)
0 引言
随着船舶电力推进技术的发展,以往的集中供电模式将被直流区域供电模式取代[1],各种状态下直流大电流测控成为电力系统安全可靠运行的基本保证。以某型直流断路器为例,额定电压5 kV,额定电流6 kA,短路时峰值电流可达75 kA,该断路器对测控传感器的要求是:实时检测稳态电流,实时跟踪故障电流(响应时间微秒级),测量回路与主回路电气隔离,有较强的抗干扰能力,传感器的体积和功率满足船舶工程化要求。
目前常用的直流大电流检测方法主要有分流器、霍尔电流传感器。分流器[2]用于船舶直流大电流检测与控制时,存在着体积大、功耗高、安装检修不便、一二次侧没有电气隔离、不能用来测量高压电路电流等问题。测量短路电流时,分流器的电感亦不可忽略。传统霍尔电流传感器有开环(直放式)和闭环(磁平衡式)两种,开环霍尔电流传感器,由于存在磁滞损耗,测量大范围变化的电流时,线性度变差。闭环霍尔电流传感器测量大电流时存在补偿电路驱动能力有限,体积大,重量重,功耗大等问题。
点阵霍尔电流传感器[8]不采用气隙铁芯聚磁,利用多个磁敏感元件直接测量被测电流在空气中产生的磁感应强度,动态范围和测量准确度仅取决于磁敏感元件霍尔片的性能,具有体积小,测量范围大,功耗小,响应快,一二次回路隔离等优点,能够满足断路器对电流测控的要求,基于此原理研制的传感器,测量范围达75 kA,半径只有24 cm,功耗比分流器和传统霍尔电流传感器要低很多。但由于没有气隙铁芯聚磁,外部磁场很容易进入传感器的霍尔元件,从而对测量准确度造成影响,外部磁场对传感器的测量准确度影响如何?就成了工程应用前必须考虑的问题。从目前检索到的中外文献看,对于点阵式霍尔电流传感器的测量误差的确定都是通过试验和仿真手段进行的,例如文献[7][8],还没有见到从机理上进行解析分析的文献,本文从机理角度剖析了外部磁场对传感器测量准确度的影响,基于导体横截面为圆形的平行电缆磁场对传感器测量准确度的影响理想模型,解析计算测量误差,试验结果表明该模型及算法能够较好反映点阵式霍尔电流传感器的抗干扰能力。
1 点阵式霍尔电流传感器模型
点阵式霍尔电流传感器的依据是一次载流导线为细长直导线的磁场分布模型,基本假设为[5]:
1) 圆柱形载流导线截面均匀,被测电流视为无限长均匀分布线电流;
2) 霍尔元件磁敏感片面积无穷小,只感应垂直穿过的磁通密度分量;
3) 霍尔元件的霍尔系数一致,即所有采用的霍尔元件在相同激励和相同磁场的作用下,产生的霍尔电势相等,把霍尔电势与激励电流和磁场强度的比值记作霍尔系数K;
4) 载流导线在霍尔元件磁敏感片所在平面上。
将多个霍尔元件对称均匀分布在一定半径的圆上,就构成了点阵式霍尔传感器的模型。图1是8点阵霍尔电流传感器模型图。
由安培环路定律知,在真空中距离线电流R处的磁通密度为

其中:μ0为真空磁导率,4π×10-7H/m;Ip为被测电流的大小,单位为A;R为被测点到载流导线中心的距离,单位为m。
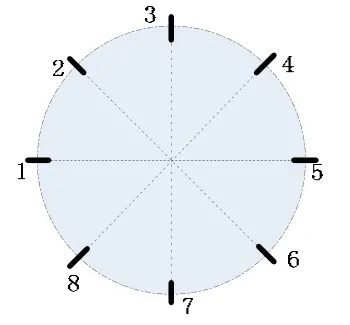
图1 8点阵霍尔电流传感器模型
对于霍尔线性元件,有EH=RHICB=KB(K=RHIC),RH为霍尔常数,单位V/AT,它的大小通常取决于霍尔芯片的材料和和几何形状;IC为驱动电流,单位为A。
设第n个霍尔元件所在点的垂向磁通密度记为Bn,由模型假设可得,各个霍尔元件的输出电势相等,总霍尔电势Es为
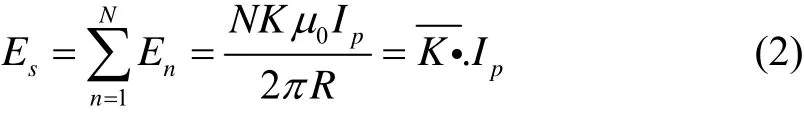
为点阵式霍尔电流传感器的输出霍尔电势与被测电流Ip之间的比例系数。
由(2)式可见,该传感器为零阶传感器,零阶传感器的输出和输入成正比,且与信号频率无关,因此无幅值和相位失真问题,零阶传感器具有理想的动态特性[6]
将(2)式变形可得:
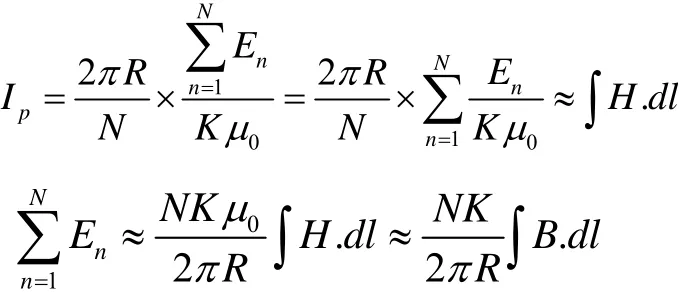
即输出信号之和是对安培环路定律的近似,当霍尔元件的数量比较多时,多个等间距均匀对称分布的霍尔元件对所在点的磁感应强度大小的累加有近似积分的效果。基于此,点阵式霍尔电流传感器是可以得到令人满意的抗干扰能力的。
2 平行导线磁场对点阵式霍尔电流传感器的测量准确度影响模型及分析
将被测电流导线穿过点阵圆心,圆柱形干扰电流导线在霍尔点阵圆外,与被测电流导线平行,两导线中心轴相距L。设被测电流为Ip,干扰电流为Id,两电流方向相同,如图2(a)中均为垂直流进纸面。点阵圆半径为R,霍尔元件2和被测电流导线、干扰电流导线在同一平面上。
由Ip∝B∝Es,则平行导线磁场引起的绝对磁场测量误差为点阵霍尔元件感应到的平行导线电流产生的磁通密度之和,可以定义测量误差e,测量误差为平行导线磁场磁通密度在垂直于霍尔元件方向上的投影分量之和与霍尔元件感应到的被测电流产生的磁通密度之和的百分比。
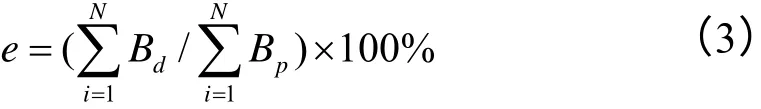
由安培环路定律,从模型图中可知,被测电流产生的磁通密度垂直穿过霍尔元件,霍尔元件感应到的平行导线电流产生的磁通密度即为将平行导线电流在霍尔元件处产生的磁通密度投影到被测电流产生的磁通密度方向上的分量。
将这些分量相加得到总的干扰磁通密ΣBdproj,参考图2(b),可得元件2感应到的平行导线电流磁通密度:Rf。
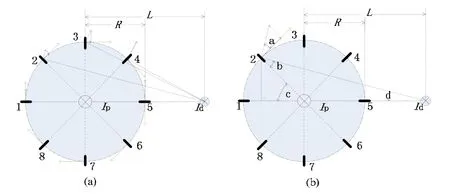
图 2 (a)平行导线磁场对传感器的测量准确度影响模型(b) 元件2感应的平行导线电流磁通密度计算
同理,可以求得其它各个霍尔元件感应到的平行导线电流磁通密度ΣBdproj。
同理可以得到N个元件时,平行导线对点阵霍尔电流传感器的测量准确度的影响。此时的测量误差为:
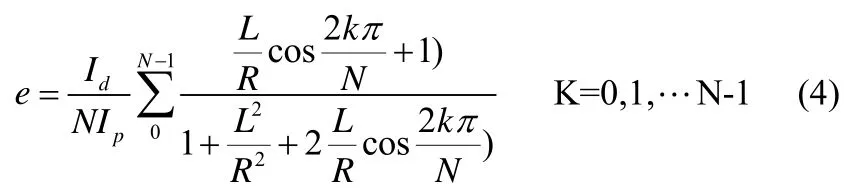
N为霍尔元件个数。
可以看到误差e与Id/Ip之比成正比;与L/R,点阵个数N都有关。
(1) 测量误差e与L/R的关系。
现以课题组研制的8点阵霍尔电流传感器为例,其实物图如图3。
有关参数如下:R=25 mm,N=8,假设Id=Ip,将参数代入(4)式,并用matlab软件画图,可得测量误差e与L/R关系如图4。

图3 8点阵霍尔电流传感器
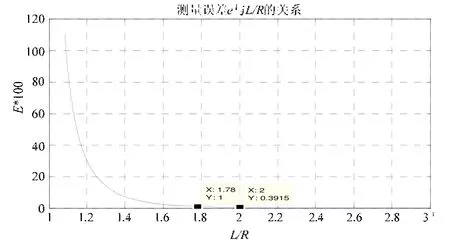
图4 测量误差e与L/R的关系
从图中可以看到测量误差e随着L/R的增大而减小,当L/R=1.78时,误差为1%,当L/R=2时,误差为0.39%。即只要平行电缆间距超过1.78倍点阵圆半径,理论上就可将误差控制在1%以内。
(2)测量误差e与点阵数N的关系
设R=25 mm,L=50 mm,Id=Ip,将参数代入(11)式,并用matlab软件画图,可得测量误差e与点阵数N的关系如图6。
从图中可看到,随着N的增大,测量误差逐渐减小,当N=8时,测量误差e=0.39%,当N=16时,e=1.526×10-5。验证了只要点阵数达到一定数量,传感器就能够得到令人满意的抗干扰能力。
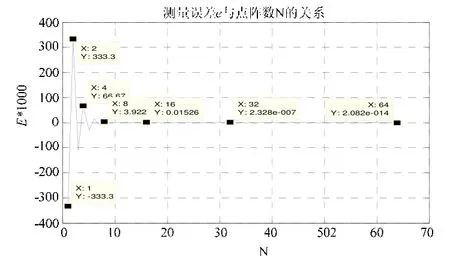
图5 侧量误差e与点阵数N关系
3 实验结果对比分析
我们采用LC充放电电路进行模拟试验,模拟试验电路见图7,通过将被测电流导线弯转回来作为干扰电流。所以有Id=Ip,C=4 mF,L=30 μH,Rf分流器,变比为1 V:1020 A,F为晶闸管,D为二极管,CHB为自制8点阵霍尔电流传感器,点阵圆半径R=25 mm,8点阵霍尔电流传感器工作电源电压为5 V,当导线无电流通过时,输出电压为2.5 V,可以进行正反向电流测量,霍尔元件的饱和磁通密度为0.08 T。
采用电容C作为试验电源,充电至460 V,控制F导通C放电,外部平行导线离点阵圆中心距离L分别为1.6R=40 mm、1.8R=45 mm、2R=50 mm,采用分流器和点阵霍尔电流传感器接到示波器测量主回路中的电流。试验波形见图8、9。
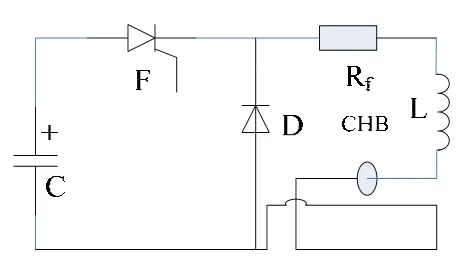
图6 试验电路
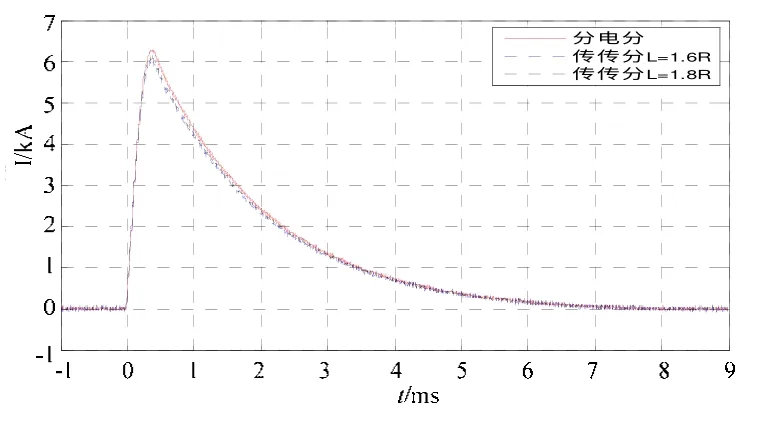
图7 L=1.6R、1.8R分流器和传感器的测量电流曲线
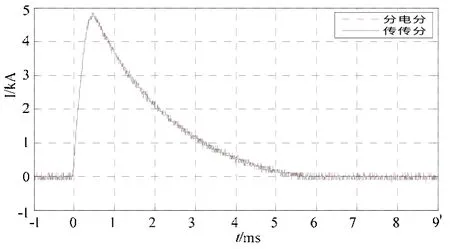
图8 L=2R分流器和传感器的测量电流曲线
以L=2R时的测量电流曲线为例,用Matlab对图中数据进行处理,可列出表1。
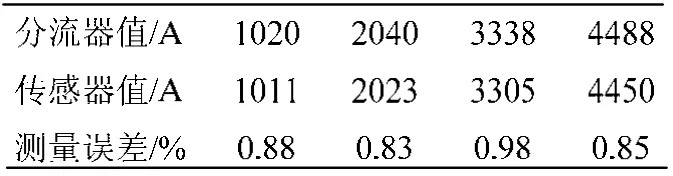
表1 实验结果
可求得L=2R时,测量误差的平均值为0.885%。
同理分别将相关参数N=8,Id=Ip,L分别等于1.6R,1.8R,2R,代入(4)式可以求得L=1.6R,L=1.8R时的测量误差。见表2。
考虑到分流器的精度,可以看出,理论误差反应了实际误差,验证了算法的正确性。

表2 实验结果
4 结论
本文基于点阵式霍尔电流传感器模型及传感器应用环境,构建外部平行导线对点阵式霍尔电流传感器的影响模型,解析得出测量误差计算方法,并自制8点阵霍尔电流传感器,设计对比试验,以分流器测量值为基准,通过分流器值与传感器测量值对比,得出实际误差,验证算法的正确性,该算法为提高传感器的测量准确度提供了方法,能够在一定条件下估算误差,也可以为点阵式霍尔电流传感器的安装、使用提供指导。
[1] 庄劲武, 张晓锋, 杨锋, 等. 船舶直流电网短路限流装置的设计与分析[J]. 中国电机工程学报, 2005, 25(20): 26-30.
[2] 李俊, 彭中华. 直流大电流测量技术研究[J]. 仪表技术, 2010,6:27-29.
[3] 工业电流电压传感器[Z]. 北京莱姆电子有限公司,P21.
[4] 宇波模块产品手册-2010/2011版[Z].北京森社电子有限公司: 12,22.
[5] 陈庆, 李红斌, 黄本雄. 点阵式霍尔电流传感器的模型及实现[J]. 华中科技大学学报(自然科学版),2009, 37(3): 9-11.
[6] 王化祥, 张淑英. 传感器原理及应用(修订版)[M].天津: 天津大学出版社, 1999: 10-17.
[7] 陈庆, 基于霍尔效应和空芯线圈的电流检测技术[D]. 华中科技大学博士论文, 2008: 22-23.
[8] J.T. Scoville, p. ipetersen, A low-cost multiple Hall probe current transducer, Rev.Sci.Instrum.62(3),March 1991, pp. 755-760.
[9] P.Ripka,P.Kejik,P.Kaspar,K.Draxler, Precise DC current sensors, Proc.of IEEE Inst. And Meas. Techn.Conf., June 4-6, 1996,pp.1479-1483.
[10] R. Bazzocchi, L. Di Rienzo, Interference rejection algorithm for current measurement using magnetic sensor arrays, sensors and actuators: A.Physical, vol.(85) 1-3, Aug. 2000, pp. 38-41.

