基于AR 功率谱和STFT的混合调制信号参数估计算法

林财永，张国毅

(空军航空大学，长春 130022)

0 引言

现代战场的电磁环境愈加复杂，对雷达的工作和生存能力提出了更为严苛的要求。传统单一的频率编码和相位编码形式已经很难满足要求。混合调制扩频技术却可以结合两者的优点，具有大的时宽带宽积和好的抗干扰性能，能够很好地满足现代电子战的要求，得到了广泛应用。因而，对这种信号的参数估计具有十分重要的意义。

常规FSK/PSK 混合调制信号通常是以频移键控为基础进行相位编码，而新型混合调制信号则是以相移键控为基础进行跳频编码［1-4］。当前，对这种新型混合调制信号的研究较少，未提出有效的参数估计方法。而常规混合调制信号的参数估计算法主要有两类，一类是对信号进行平方处理，将两种调制的作用相互独立再进行参数估计［5-6］;另一类是对信号进行谱相关的算法处理［7-8］。但是，上述方法却存在以下问题，一是平方处理后信号的信噪比降低约6 dB，使得算法对信号的信噪比要求较高;二是谱相关算法对信号的参数取值范围有限制，并且对伪码参数估计的精度不高［9］。

针对上述问题，本文提出了一种基于AR 功率谱和短时傅里叶变换(Short Time Fourier Transform，STFT）的联合估计算法。首先，计算信号的AR 功率谱。AR 功率谱对信号的相位不敏感，可以估计出混合信号中的跳频个数和跳频值。接着计算信号的STFT，快速得到信号的时频分布。然后，提取时频分布中对应跳频值切面，利用切面峰值包络计算信号的相位码元宽度。根据码元宽度，将混合信号拆分为独立的Costas信号。结合估计出的跳频个数，计算出Costas信号的码元宽度，从而完成对这种新型混合调制信号的参数估计。最后，在高斯噪声环境下对算法进行了仿真，验证了本文算法的有效性。

1 信号模型

新型FSK/PSK 混合调制信号的调制原理是先对一个长度为T的脉冲信号进行N 位的相位编码，编码序列为{C1，C2，C3，…，CN}，每个码元宽度为t1，且满足T=Nt1。然后，在每个码元内再进行M个频点的跳频编码，编码序列为Costas 序列{f1，f2，…，fM}，子码宽度满足t2=t1/M。信号的编码规律如图1所示。

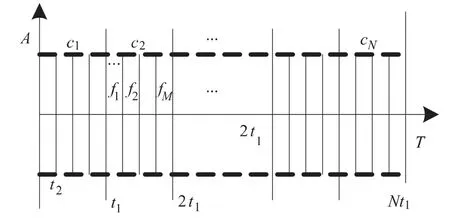
图1 新型FSK/PSK信号的调制规律

由图1 可以看出，新型FSK/PSK 混合调制信号是在多个Costas信号之间进行N个连续二相编码，新型FSK/PSK 混合调制信号的表达式［4］为

式中fi按照Costas 编码序列进行改变。

2 算法原理

2.1 信号的AR 功率谱

新型FSK/PSK 混合调制信号的傅里叶变换由于受到相位变换的影响，导致频率的谱峰数不稳定。采用AR 功率谱估计的方法却可以有效避免混合调制信号中相位编码对信号谱峰个数估计的干扰。同时AR功率谱对干扰噪声具有较低的敏感性，在数据较短或不完全平稳时一样能够获得良好的估计精度［10］。

本文的AR 功率谱采用Burg 递推法。它克服了Levenson 递推法需要先由观测数据估计自相关函数的缺点，利用前向预测误差和后向预测误差之和最小的原则计算AR 模型的参数，即直接由信号观测数据计算AR 功率谱［11］，提高了精度。图2、图3分别给出了11-6FSK/PSK 新型混合调制信号的FFT和AR 功率谱图。

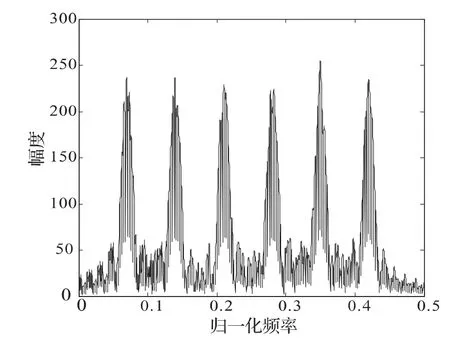
图2 FSK/PSK信号的FFT

图3 FSK/PSK信号的AR 功率谱

从图2 可以看出，由于受到相位编码的影响，信号的频谱峰值个数与信号实际的调制频率个数不同，并且频率值估计精度较差。而信号的AR 功率谱则不受相位编码的影响，通过计算峰值个数和对应位置就可以很好地估计出跳频个数M和跳频值fi。

2.2 相位码元宽度估计

考虑到AR 功率谱估计频率精度较高，降低了对时频分布精度的要求，因此选用对多分量信号不产生交叉项并且易于工程实现的STFT来获取信号的时频分布矩阵。提取时频分布矩阵中对应fmax的切面，代入公式(4）得到切面峰值包络，即

其中频率fmax是AR 功率谱中估计出的能量最大的一个跳频值，由公式得到的STFT 切面包络如图4所示。

从图4 频率fmax的包络峰值可以估计出信号相位编码的码元宽度。首先，将包络峰值点依次标记为p1，p2，…，pn对峰值点做一级差记为△1，△2，…，△n－1。根据统计平均公式(5），求出一级差△的均值。

图4 频率fi的时频分布切面包络图

式中的长度均是在采样频率下得到的点数。

2.3 频率码元宽度估计

由公式(1）知道，混合调制信号在单个相位码元内可以看作是Costas 编码信号。因此，将混合调制信号按照相位码元宽度进行拆分，可以得到N个独立的Costas 编码信号，除了初始相位不同外，信号的其他参数是完全一致的。

2.4 算法流程图

FSK/PSK信号的参数估计算法流程图如图5所示。

图5 FSK/PSK信号参数估计算法流程图

3 仿 真

本节将通过仿真验证并分析本文算法的性能。选取两种新型混合调制信号7-6FSK/PSK和13-10FSK/PSK，长度分别为21 μs和65 μs，Costas 码序列为{3 2 6 4 5 1}和{2 4 8 5 10 9 7 3 6 1}，载频为10 MHz，采样频率为100 MHz，相位编码均采用Barker 码。对两组信号进行1000 次Monte Carlo 仿真，将不同信噪比下参数估计的性能分析结果同克拉美-罗下限(Cramer-Rao lower bound，CRLB）进行比较。因混合调制信号的CRLB的解析式推导不易，这里用具有相同调频规律的Costas信号的CRLB 作为跳频编码个数、跳频值和跳频码元宽度的参照项，用相同参数的Barker信号的CRLB 作为相位码元宽度的参照项。仿真结果如图6所示。

从图6中可以看出，本文算法对新型FSK/PSK 混合调制信号的参数估计是有效的，具有较高的精度和抗噪性，并且接近CRLB。当信噪比大于－5 dB时，算法的性能明显提高，但是信噪比超过一定临界值后估计精度不再增加。对比两组信号的估计精度可以发现，7-6FSK/PSK信号的估计精度略高于13-10FSK/PSK信号的估计精度，这主要是因为13-10FSK/PSK中的调制参数相比于7-6FSK/PSK信号更加复杂，受噪声干扰影响更加严重。

图6 不同信号的参数估计性能比较

4 结束语

本文研究了一种新型FSK/PSK 混合调制信号的参数估计问题。提出了一种AR 功率谱和短时傅里叶变换的联合估计算法，将信号拆分为多个独立Costas信号，大大简化了参数估计过程。仿真验证了该算法可以在较低信噪比下完成信号的参数估计。本文算法不仅保留了AR 功率谱和短时傅里叶变换算法处理非平稳信号的优点，同时计算简单，易于工程实现，具有重要的实际意义。

［1］池文静，陈健，阔永红.FSK/PSK 复合调制雷达信号的识别［J］.应用科学学报，2011，39(3）:256-260.

［2］J Patrick Donohe，Franklin M Ingels.The ambiguity properties of FSK/PSK signals//IEEE international radar conference，1990.

［3］郭贵虎，文贻军，戴天.一种新型低截获FSK/PSK雷达信号分析［J］.电视技术，2009，49(8）:49-53.

［4］李英祥，周先敏.一种具有LPI 特性的雷达信号—新的FSK/PSK信号［J］.信号处理，2002，18(2）:177-179.

［5］雷雪梅，杨万麟，吕镜清.FH/PSK 混合调制扩频信号参数估计［J］.火控雷达技术，2009，38(4）:40-44.

［6］雷雪梅，吕镜清，杨万麟，付海涛.FSK/PSK 混合调制信号多参数估计［J］.电子信息对抗技术，2009，24(6）:9-13.

［7］熊刚，赵惠昌，林俊.伪码-载波调频侦察信号识别的谱相关方法(Ⅰ）——伪码-载波调频信号的谱相关函数［J］.电子与信息学报，2005，27(7）:1081-1086.

［8］熊刚，赵惠昌，王李军.伪码-载波调频侦察信号识别的谱相关方法(Ⅱ）——伪码-载波调频信号的谱相关函数［J］.电子与信息学报，2005，27(7）:1087-1092.

［9］林俊，熊刚，王智雪.基于时频分析的伪码与线性调频复合体制侦察信号参数估计研究［J］.电子与信息学报，2006，28(6）:1045-1048.

［10］胡广书.数字信号处理——理论、算法与实现［M］.北京:清华大学出版社，2003:527-574.

［11］李明宴，张鲁筠，江铭炎，许建华，张超.复杂脉内调制雷达信号的识别方法［J］.计算机工程与应用，2011，47(15）:156-160.

［12］陈秋华，王斌.低信噪比下跳频信号的跳速估计［J］.信息工程大学学报，2008，9(4）:397-400.

［13］袁伟明，王敏，吴顺君.一种新的Costas 跳频信号参数估计法［J］.电路与系统，2007，12(4）:60-63.

［14］张鑫，艾勇军，黄宇.Costas 编码信号的循环谱特征分析与参数估计［J］.海军航空工程学院学报.2011，26(4）:427-431.