深度脑刺激的精确闭环去同步控制

王 江，伊国胜，边洪瑞，韩春晓，李会艳，魏熙乐，邓 斌

(1. 天津大学电气与自动化工程学院，天津 300072；2. 中国船舶重工集团公司707研究所，天津 300131；3. 天津职业技术师范大学自动化与电气工程学院，天津 300222)

深度脑刺激的精确闭环去同步控制

王 江1，伊国胜1，边洪瑞2，韩春晓3，李会艳3，魏熙乐1，邓 斌1

(1. 天津大学电气与自动化工程学院，天津 300072；2. 中国船舶重工集团公司707研究所，天津 300131；3. 天津职业技术师范大学自动化与电气工程学院，天津 300222)

深度脑刺激(DBS)是治疗帕金森症和癫痫等神经疾病的有效方法之一．针对其开环控制的缺点，以Morris-Lecar神经元为节点模拟病态同步神经元网络，提出了基于H∞变论域模糊的DBS闭环控制方法，实现了神经元网络的精确去同步控制．采用变论域模糊逼近神经元非线性动态和H∞抑制逼近误差，利用李雅普诺夫稳定性理论证明控制算法的稳定性并进行了仿真分析．仿真结果验证了所提方案的有效性及鲁棒性，该方法可作为由病态同步引起的神经疾病的一种潜在电刺激治疗方案．

深度脑刺激；去同步；闭环控制；变论域模糊

神经网络的病态同步是帕金森症和癫痫等神经疾病的主要表现之一[1-2]．为了缓解和治疗这类疾病，通常采用药物、电磁刺激[3]和深度脑刺激[4](deep brain stimulation，DBS)等方法，实现神经网络的去同步．其中，DBS疗法主要是将刺激电极通过立体定向技术、微电极记录技术插入脑内特定核团，用持续的高频脉冲电刺激抑制不正常的脑核团放电，进而达到治疗效果[5]．本质就是通过外电场来改变神经网络的状态．DBS具有可调节性、可逆性等特点[6-7]．到目前为止，DBS已经在原发性震颤、帕金森病、癫痫、抑郁症等神经疾病的临床治疗中取得了良好效果．

从控制系统角度来说，目前的DBS相当于一个开环控制，控制器的参数主要通过人工网格法调整．事实上，DBS的参数和治疗效果之间存在着复杂的关系，采用开环控制不能保证在有限时间内找到合适的参数．例如，在对神经元集群的去同步过程中，很难选择合适的刺激信号使得每个神经元放电的相位差达到所期望的值，并且易导致一些重要放电丢失的问题[8]．因此，迫切需要结合控制理论和最优控制方法，设计刺激参数自适应调节的闭环DBS控制方法．Tass课题组[9-13]利用Hodgkin-Huxley(HH)、Morris-Lecar(ML)等模型模拟病态同步神经元网络，采用时滞反馈方法实现了去同步控制，并且已有物理装置问世．这种方法简单实用，即通过采用相位方程加入扰动实现去同步．然而该方法不能将各神经元的相位差稳定到所期望的状态，并且若疾病使神经元或核团的放电模式发生了改变或掺杂了外界的未知刺激，那么该方法无法有效地将网络中神经元或核团的放电模式调节至正常状态．因此需要对控制算法进行优化，使其在更多更复杂的情况下能够适用．

在传统的控制中，被控对象的数学模型必须已知．而模糊控制法将模糊函数作为万能逼近器，用TS模糊系统逼近混沌系统，进而得到系统理论要求的模糊控制器[14]，随着误差动态调整的论域则有效地优化了逼近效果．变论域模糊控制方法可以有效地消除控制过程中非线性、高阶次、时变性及随机干扰等因素的影响[15]，达到预期的控制目标．H∞最优控制理论可以有效地处理稳定性和扰动问题[16]．当结合二者设计控制器时，变论域模糊控制可起到“粗调”的作用，H∞控制可起到“微调”的作用，这样控制器不仅保证了系统的稳定性，而且将逼近误差和外部扰动对跟踪误差的影响减小到任意给定的标准．

笔者通过理论分析提出了变论域模糊与H∞相结合的控制方法，并根据李雅普诺夫稳定性理论证明了系统的稳定性．以ML神经元为节点构建全耦合的神经元网络模拟病态同步神经元网络，利用H∞变论域模糊控制器实现该网络中任意一个神经元与参考神经元的同步，再实现网络中每2个神经元的相位差跟踪预先给定的参考相位差，最终按指定相位差实现网络的精确去同步控制，而且当网络中存在离子通道噪声时依然可以准确地实现去同步控制．理论分析和数值仿真都验证了所提方案的可行性和有效性．

1 Morris-Lecar模型及其网络的建立

ML模型的建立是为了描述北极鹅肌肉纤维的细胞特性[17]．经实验发现，北极鹅的肌肉细胞膜电压与细胞膜中的通道和K+通道相关的电压组成有关，可以通过一个二阶非线性微分方程来描述，即

式中：Iext为外加直流电流；V为细胞膜电位；W为K+通道打开的概率；M∞和W∞分别为Ca2+和K+在稳定状态时开通的概率；Cm为细胞膜电容；gCa、gK、和gL分别为钙电导、钾电导和漏电导的最大值，反映了各个离子细胞膜两侧的浓度；VCa、VK和VL分别为Ca2+，K+和漏电流的平衡电势；τW为钾离子激活变量的时间常数．其中

神经元振荡通常表现为2种不同的时间尺度：以持续峰放电为特征的快时间尺度和以簇放电为特征的慢时间尺度．本文利用ML簇放电模型研究网络去同步问题，将式(2)中引入慢钾离子电流

神经元之间的通信以突触作为媒介，突触连接方式有电突触连接和化学突触连接[19-21]．神经元通过突触按照一定的拓扑结构和连接方式相互联结成一个网状的系统即为神经网络．神经网络有不同的连接方式，如小世界网络、随机网络等，文献[22]给出了所有42种三神经元网络的结构图．本文提出的去同步控制方法适用于任何一种网络，即不依赖于网络的结构和突触连接形式．仿真分析以电突触连接的全耦合ML神经元网络为例，网络中第i个神经元可表示为

式中：gsyn,ij为第i个神经元与第j个神经元的耦合强度；N为网络中神经元的个数．通过调节gsyn,ij的大小可以实现网络中神经元的同步．

2 H∞变论域模糊控制

同步是癫痫、帕金森等疾病的典型特征，神经元的编码方式主要是通过放电频率决定的，放电的峰峰间期承载着神经元的信息，因此对于治疗癫痫、帕金森等疾病，最重要的是将其神经元放电时峰值的间隔调节至正常状态．根据此原理，本文提出的闭环DBS去同步控制如图1所示，核心为同步(虚线)与去同步(实线)控制器的设计，箭头的方向为信号传输的方向．为了实现病态网络的去同步，只需知道病态网络中每个神经元及参考神经元的膜电位，基于H∞变论域模糊规则设计同步与去同步控制器，并施加在病态网络中每个神经元上，则网络将按照给定的相位差实现精确去同步．

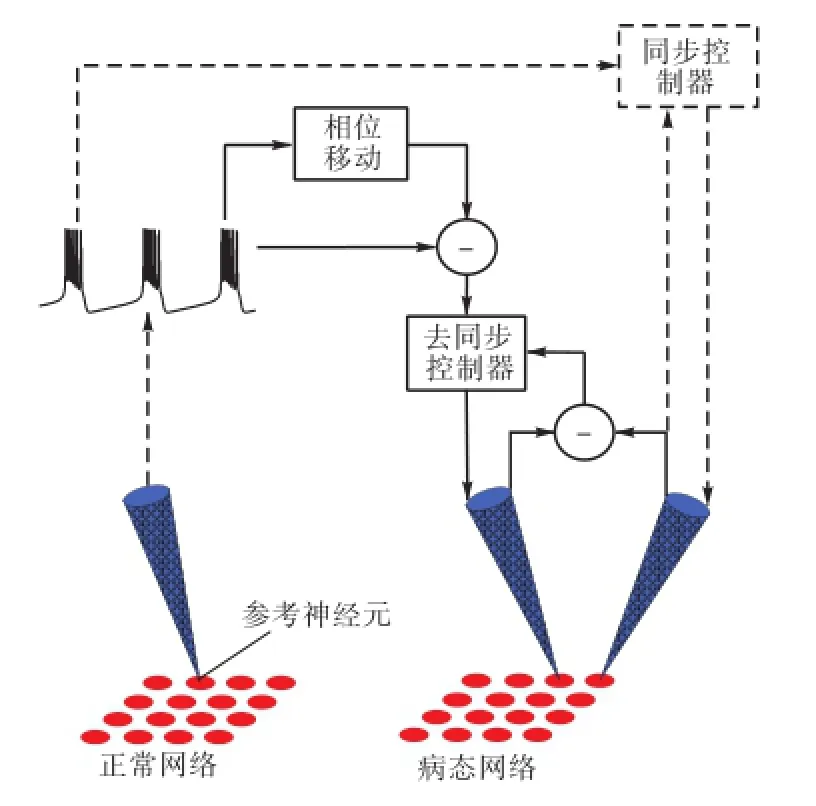
图1 闭环DBS去同步控制Fig.1 Close-loop desynchronization control in DBS

去同步方法设计的主要思想如图2所示．首先，从正常网络中选择膜电位已知的参考神经元1，将参考神经元1的膜电压Vref1的相位向后移动T/ N，其中T为神经元簇放电的周期，得到参考神经元2的膜电压Vref2；然后，求得参考神经元1和2的膜电压之差eref1=Vref1- Vref2，再将eref1的相位依次移动N-2个T/ N，共得到N-1个误差erefi(i=1,2,…,N -1)作为病态网络去同步控制中的参考误差；最后，采用H∞变论域模糊方法设计同步与去同步控制器，利用同步控制器实现病态网络中第1个神经元与参考神经元1同步，利用去同步控制器实现病态网络中N个同步神经元的N-1个误差跟踪参考误差erefi(i=1,2,…,N -1)的轨迹，最终使N个同步的神经元进入给定的N个状态，从而实现精确去同步．

图2 闭环去同步方法的整体思路Fig.2 Close-loop desynchronization method

2.1 同步控制器的设计

模糊控制器具有万能逼近特性，变论域是指输入和输出的基本论域随控制需求按一定准则在适当的时刻进行伸缩变化，定义在基本论域上的模糊划分也随之变化．论域随着误差的动态调整可有效地优化逼近效果，添加的H∞控制更加有效地消除模糊逼近和外界扰动之间的稳态误差．

下面以2个神经元为例阐述H∞变论域模糊同步控制器的设计，控制从神经元(下标为2)跟随主神经元(下标为1)的动态，为不失一般性，将主从神经元系统表示为

式中：x1和x2为n维状态向量，x，x2∈Rn；Ax代表线性部分；Βg(x)代表其非线性部分；A和B为常数矩阵，A∈Rn×Rn,B∈Rn，且有而g: Rn→R为有界非线性平滑函数，u∈R为控制输入，d0∈R为有界扰动．

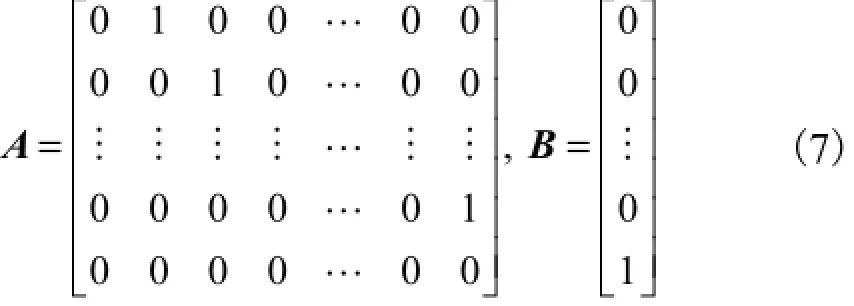
令e=x2-x1为系统同步误差，则同步误差的动态表示为

则式(8)变为

故可通过适当选择控制增益kT使特征多项式矩阵A-BkT是严格Hurwitz的．

但()f x和0d通常未知，因此主动反馈控制器*u无法得到．本文提出变论域模糊控制器Fu直接逼近的控制律为

加入H∞控制器u∞用于消除模糊逼近误差和外部扰动，即设计混合控制器u=uF+u∞．

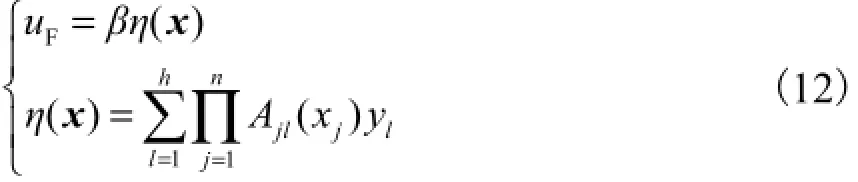
式中：Xj为输入变量xj的论域，(j=1,2,…,n)；Y为输出量y的论域上的模糊分割；{Bl}(1≤l≤h)为Y上的分割，隶属度表示“xj是Ajl(xj)”的“可信度”；yl为规则l的权中心；β为伸缩因子．

根据万能逼近定理，uF=βη(x)能够以任意精度逼近紧集Ωx上的任意连续函数u，形式为

c差，最佳伸缩因子β*定义为

式中βΩ为β的期望边界．

在控制器设计过程中，由于β*通常未知，需要估计，令βˆ为β*的估计，β˜=βˆ-β*表示估计误差，则式(8)改写为

式中ξ=d-ξc．

选取李雅普诺夫函数

式中权矩阵P=PT＞0，标量γ＞0为自适应增益．对式(16)两端进行微分后得

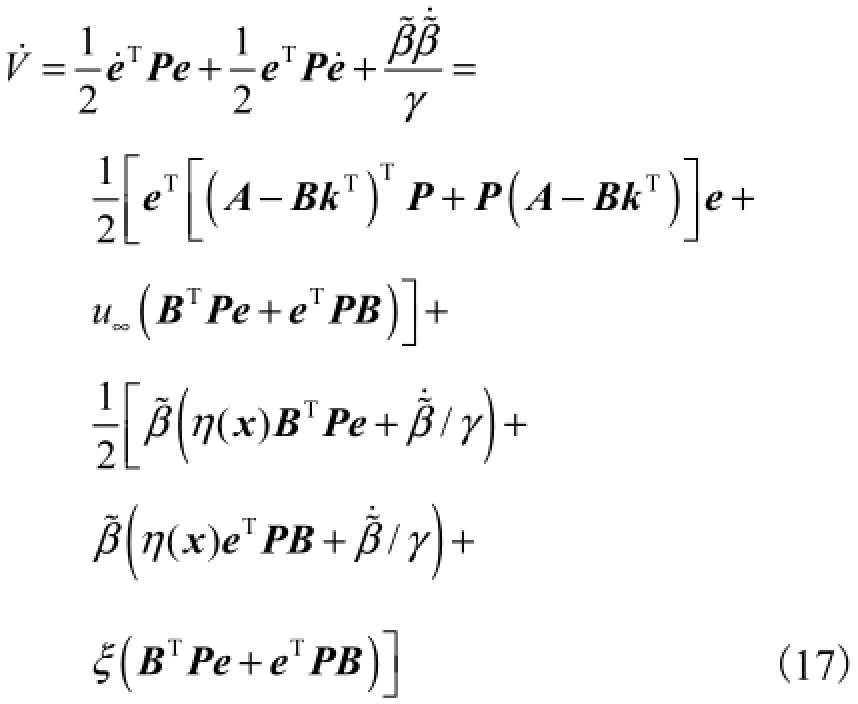
选择H∞控制器u∞为

式中0r＞是控制增益，矩阵P选择为Riccati-like方程的解，即

式中：T0=＞

QQ为权矩阵；ρ为容许误差．

选择自适应率来在线调节β，其计算式为

将式(18)、式(20)代入式(17)，可得

对式(21)两边进行积分得

由于V( T)≥0，则

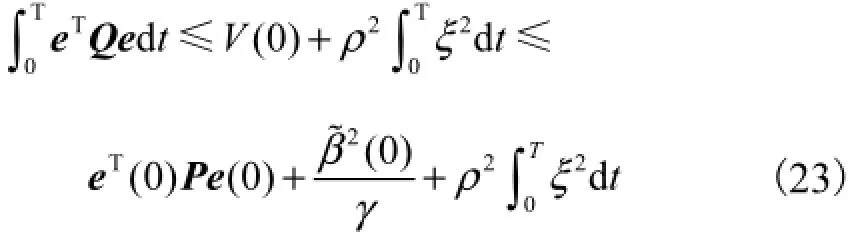
这样，对于给定的容许误差水平ρ，控制器能实现H∞跟踪性能．因此，根据李雅普诺夫稳定性定理，只要选择合适的参数就可以保证误差系统是大范围一致渐进稳定的．

2.2 去同步控制器的设计

去同步控制器设计的目的是使病态同步网络中每2个神经元的误差跟踪给定的参考误差，最终实现网络的精确去同步．以2个神经元为例，将参考误差及网络中2个神经元之间的误差表示为

定义同步误差21-e=ee，则动态方程为

H∞控制器为

3 仿真分析

3.1 病态同步神经元网络的建立

以3个ML神经元组成的全耦合网络为例，利用Matlab软件进行仿真分析．图3为耦合强度g=0 mS/cm2时，参考神经元1及网络中3个神经

syn,ij元的原始放电模式．初始状态分别为：xref=x3=[-29,0,0.39]，网络中神经元的外加电流Iext,i=参考神经元的外加电流I=50μ A/cm2．从图3中可以看出，4个神经元为周

ext期放电且相互之间不同步．

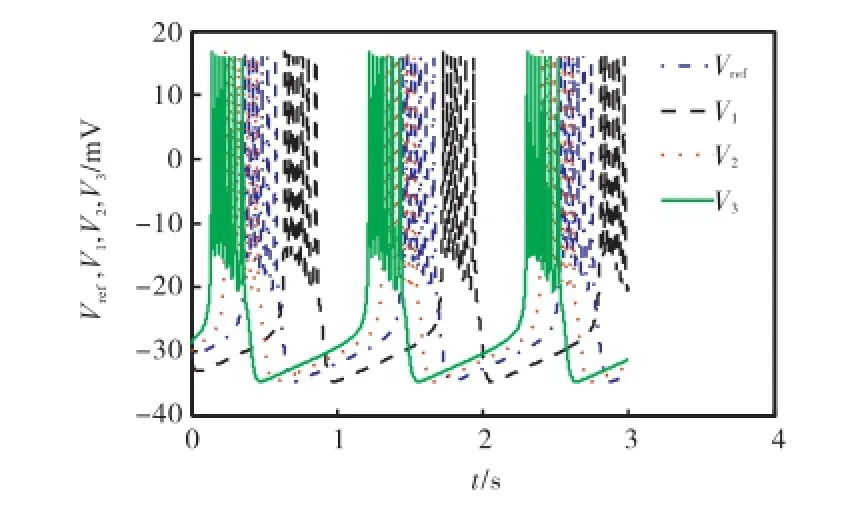
图3 参考神经元1及网络中3个神经元原始的膜电位Fig.3 Original membrane potentials of three neurons in the network and reference neuron 1

选择耦合强度gsyn,ij=0.5 mS/cm2来模拟病态同步神经元网络，如图4所示．图4(a)为病态神经网络中3个神经元的放电波形，3个神经元完全同步；图4(b)为神经元1与2，神经元2与3的膜电位误差曲线．从图4中可以看出，随着仿真时间的增加，2个误差将趋于0．因此通过调节耦合强度gsyn,ij可使网络中所有神经元达到同步．

图4 病态同步神经网络的动力学特性Fig.4 Dynamics of neural network under the condition of abnormal synchronization

3.2 网络的去同步控制及其鲁棒性

为使病态同步神经网络实现去同步，本文在t=2.4s 时，对网络中任意一个神经元施加H∞变论域模糊同步控制器，同时对网络中其他神经元施加H∞变论域模糊去同步控制器．其中同步控制器的参数选择为：Q=10，γ=1，ρ=0.1，r=0.02，则P=5，ML神经元的膜电压范围是[-40 mV,20 mV]，x在此范围上取7个模糊子集，隶属度函数选择为

图5为参考神经元的膜电位refV、网络中某个神经元施加同步控制后的膜电位1V以及二者之差即同步误差e的波形．从图5中可以看出，同步控制器加入后，2个神经元能够快速同步，误差e趋于0．因此，H∞变论域模糊控制方法能够迫使原本不同步的神经元达到完全同步．

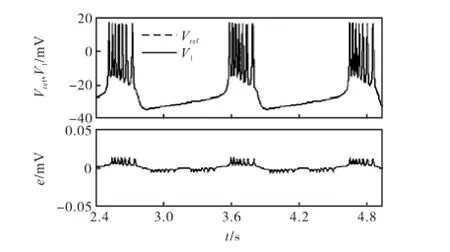
图5 网络中任意一个神经元与参考神经元1同步后的膜电位及误差Fig.5 Membrane potentials and the error of a neuron in the network and reference neuron 1 after synchronization

去同步控制器的参数选择为：Q=10，γ=1，ρ=0.1，r=0.02，则P=5，2个ML神经元膜电压之差的范围是[-60 mV,60 mV]，e在此范围上取7个模糊子集，隶属度函数选择为

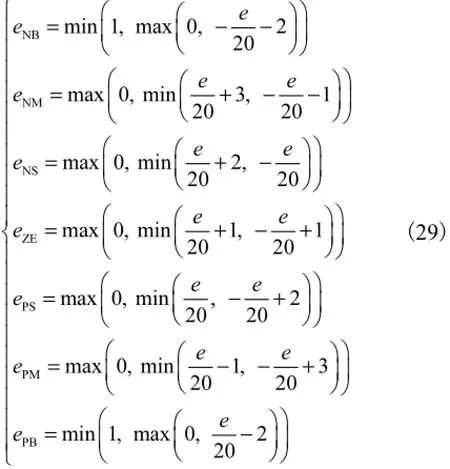
图6为施加同步与去同步控制器后网络中神经元的放电波形以及2,399.9,ms到2,400.1,ms放电波形的局部放大，在2.4st＞时3个神经元的膜电位之间存在着固定的相位差，变得不同步，网络中神经元能够按照给定的模式进行放电，说明本文提出的方法能够实现精确的去同步．同时，从同步状态到不同步状态只需不到0.1,ms的时间，如图6所示．

图6 病态同步网络去同步后的放电波形Fig.6 Spiking patterns of abnormal synchronization network after desynchronization

如图7所示，2.4st＜时，为病态同步神经元的放电波形；2.4st=时，在病态同步神经元网络中的钙电导Cag、钾电导Kg和漏电导Lg处分别引入噪声0.9sin(1.5)t、1.7sin(1.4)t和0.6sin(0.8)t，放电波形分别如图7(a)～7(c)所示，神经网络的同步现象依然存在，且放电模式发生了改变；在3.9st=时，分别加入H∞变论域模糊同步与去同步控制器．从图7中可以看出，噪声的引入不会对去同步控制产生影响，此时去同步控制的效果与未引入噪声(见图6)时控制的效果一样，说明本文提出的控制方法具有鲁棒性．

4 结 语

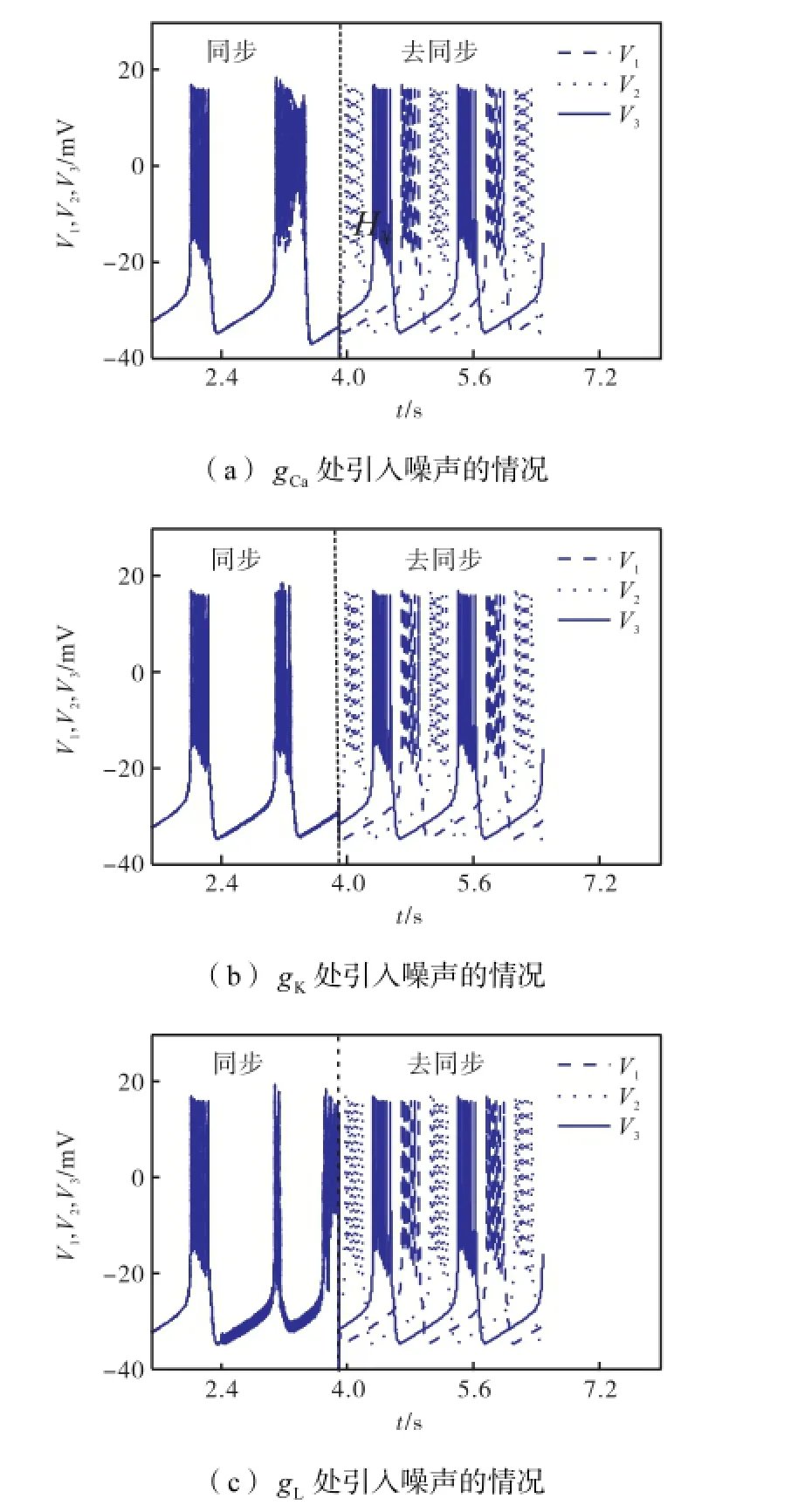
图7 噪声对病态同步网络的放电波形及去同步的影响Fig.7 Effect of noise on spiking patterns and desynchronization of abnormal synchronization network

应用变论域模糊与H∞相结合的方法设计同步与去同步控制器，旨在解决神经网络中的病态同步问题．针对DBS的开环控制，本文首先以ML神经元为节点构建全耦合的神经元网络，通过调整耦合强度来模拟病态同步神经元网络；然后，通过理论分析设计了H∞变论域模糊同步与去同步控制器，并根据李雅普诺夫稳定性理论证明了系统的稳定性；最后，通过仿真模拟了闭环控制．仿真结果证明本文提出的去同步思想能够很好地实现病态同步网络的精确去同步控制，同时证明该方法的鲁棒性，即网络中出现离子通道噪声或外部噪声等依然可以实现精确去同步控制，这为DBS刺激方案的设计和改进提供了思路．

［1］ Uhlhaas P J，Singer W. Neural synchrony in brain disorders：Relevance for cognitive dysfunctions and pathophysiology[J]. Neuron，2006，52(1)：155-168.

［2］ Uhlhaas P J，Singer W. Abnormal neural oscillations and synchrony in schizophrenia[J]. Nat Rev Neurosci，2010，11(2)：100-113.

［3］ 伊国胜，王 江，魏熙乐，等. 静态直流电场作用下神经元放电动力学分析[J]. 天津大学学报，2012，45(12)：1096-1104.

Yi Guosheng，Wang Jiang，Wei Xile，et al. Dynamical analysis of firing patterns exhibited by neuron exposed to static direct current electric field[J]. Journal of Tianjin University，2012，45(12)：1096-1104 (in Chinese).

［4］ Kringelbach M L，Jenkinson N，Owen S L，et al. Translational principles of deep brain stimulation[J]. Nature Reviews Neuroscience，2007，8(8)：623-635.

［5］ Vitek J L. Mechanisms of deep brain stimulation: Excitation or inhibition[J]. Movement Disorders，2002，17(3)：69-72.

［6］ Liker M A，Won D S，Rao V Y，et al. Deep brain stimulation：An evolving technology[J]. Proceedings ofthe IEEE，2008，96(7)：1129-1141.

［7］ Berger T W，Gerhardt G，Liker M A，et al. The impact of neurotechnology on rehabilitation[J]. IEEE Reviews in Biomedical Engineering，2008，1：157-197.

［8］ Hauptmann C，Popovych O，Tass P A. Demandcontrolled desynchronization of oscillatory networks by means of a multisite delayed feedback stimulation[J]. Comput Visual Sci，2007，10(2)：71-78.

［9］ Hauptmann C，Popovych O，Tass P A. Effectively desynchronizing deep brain stimulation based on a coordinated delayed feedback stimulation via several sites：A computational study[J]. Biol Cybern，2005，93(6)：463-470.

［10］ Hauptmann C，Omel'chenko O. Control of spatially patterned synchrony with multisite delayed feedback[J]. Phys Rev E，2007，76：066209.

［11］ Omel'chenko O E，Maistrenko Y L，Tass P A. Chimera states induced by spatially modulated delayed feedback[J]. Phys Rev E，2010，82：066201.

［12］ Popovych O V，Hauptmann C，Tass P A. Effective desynchronization by nonlinear delayed feedback[J]. Phys Rev Lett，2005，94：164102.

［13］ Tass P A，Hauptmann C. Therapeutic rewiring by means of desynchronizing brain stimulation[ J]. Biosystems，2007，89(1/2/3)：173-181.

［14］ Tan W，Wang Y N，Duan F，et al. LMI-based output feedback fuzzy control of chaotic system with uncertainties[J]. Chin Phys，2006，15(11)：2529-2534.

［15］ 张巍巍，王 京，王 慧，等. 混沌系统的变论域模糊控制算法研究[J]. 物理学报，2011，60(1)：010511.

Zhang Weiwei，Wang Jing，Wang Hui，et al. Research on the variable universe fuzzy algorithm of chaotic systems[J]. Acta Phys Sin，2011，60(1)：010511(in Chinese).

［16］ 王兴元，孟 娟. 基于Takagi-Sugeno模糊模型的超混沌系统自适应投影同步及参数辨识[J]. 物理学报，2009，58(6)：3780-3787.

Wang Xingyuan，Meng Juan. Adaptive projective synchronization and parameter identification of Takagi-Sugeno fuzzy huperchaotic systems[J]. Acta Phys Sin，2009，58(6)：3780-3787(in Chinese).

［17］ Morris C，Lecar H. Voltage oscillations in the barnacle giant muscle fiber[J]. Biophys J，1981，35(1)：193-213.

［18］ Chen Y Y，Wang J，Che Y Q，et al. Unidirectional Synchronization of Morris-Lecar neurons via adaptive H∞control [C]//Proceedings of the 29th Chinese Control Conference. Beijing，China，2010：749-754.

［19］ Arecchi F T. Chaotic neuron dynamics，synchronization and feature binding[J]. Physica A，2004，338(1/2)：218-237.

［20］ Belykh V N，Osipov G V，Petrov V S，et al. Cluster synchronization in oscillatory networks[J]. Chaos，2008，18(3)：037106.

［21］ Birzu A，Krischer K. Resonance tongues in a system of globally coupled FitzHugh-Nagumo oscillators with time-periodic coupling strength[J]. Chaos，2010，20(4)：043114.

［22］ Leite M C A，Golubitsky M. Homogeneous three-cell networks [J]. Nonlinearity，2006，19(10)：2313-2363.

Accurate Close-Loop Desynchronization Control of Deep Brain Stimulation

Wang Jiang1，Yi Guosheng1，Bian Hongrui2，Han Chunxiao3，Li Huiyan3，Wei Xile1，Deng Bin1
(1. School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2. No.707 Research Institute，China Shipbuilding Industry Corporation，Tianjin 300131，China；3. School of Automation and Electrical Engineering，Tianjin University of Technology and Education，Tianjin 300222，China)

Deep brain stimulation(DBS)is one of the effective treatments of neurological diseases，such as Parkinson and Epilepsy. However，most of the methods based on DBS are open-loop algorithm. To overcome the shortcomings of the open-loop control，a close-loop DBS control algorithm based on variable universe fuzzy H∞was proposed to accurately desynchronize an abnormal synchronization neural network composed of Morris-Lecar models. Variable universe fuzzy controllers were used to approximate nonlinear dynamic of neurons and H∞controllers were added to constrain the approximation error. Stability of the proposed algorithm was also proved by Lyapunov stability theory. Simulation results show the effectiveness and robustness of the proposed algorithm. This control algorithm may provide a potential electrical stimulation therapy on neurological diseases caused by abnormal synchronization.

deep brain stimulation；desynchronization；close-loop control；variable universe fuzzy

TK421

A

0493-2137(2013)11-0969-08

DOI 10.11784/tdxb20131104

2011-07-06；

2012-08-31.

国家自然科学基金重点资助项目(50537030)；国家自然科学基金资助项目(61072012，61172009，61374182)；天津市自然科学基金重点资助项目(13JCZDJC27900).

王 江（1964— ），男，博士，教授.

王 江，jiangwang@tju.edu.cn.