基于分量分离方法的地震动反应谱

徐龙军，赵国臣，谢礼立

(哈尔滨工业大学（威海)土木工程系，威海 264209）

基于分量分离方法的地震动反应谱

徐龙军，赵国臣，谢礼立

(哈尔滨工业大学（威海)土木工程系，威海 264209）

地震动反应谱统计分析中存在的离散性一直是影响设计谱精确估计的重要因素．地震动加速度反应谱离散性偏大的区段主要集中于长周期部分．为了进一步研究地震动反应谱及其长周期段的特征，建立了一个综合强地震动数据库，考虑地震动反应谱的特征将强震记录分为普通型和低频型2类，采用数字滤波方法将低频型地震动中的长周期分量分离，引入了一种2阶段平稳简谐地震动模型用于等效所分离的低频分量．结果表明：滤波后的低频型地震动与普通型地震动反应谱仍有明显差别；低频型地震动与分离后得到的低频分量以及高、中频分量参数间存在一定的相关性；指出普通型地震动与低频型地震动的设计谱须分别单独标定，其中普通型地震动设计谱采用平均谱标定，低频型地震动设计谱可以在普通型地震动设计谱标定方法的基础上对长周期段进行修正得到．该研究为地震动反应谱特征及规律的认识提供了新的方法，为设计谱的精确标定提供了参考和依据．

地震动；简谐地震动；地震动分解；抗震设计谱

抗震设计谱是基于对以往地震动反应谱的统计分析，经规准化、平均化、平滑化和经验化“四化”过程处理而成的一种对未来地震作用大小的估计[1]．事实上，由于影响地震动反应谱的因素既多且十分复杂，要针对某一种具体情况给出精确的设计谱是十分困难的，以至世界各国采用的抗震设计谱之间不仅存在明显的差异，而且普遍存在大量的不确定性[2]．

地震动反应谱的传统研究方法多是先将地震动按影响因素(如场地条件、震级、距离等)分类，再将分类地震动反应谱分别统计分析，以期能够获得较为稳定的统计结果[3-5]．但即使是分类后的地震动，其反应谱曲线也存在明显的离散性，近期发生的大震级地震动都呈现出一些新的特征，更进一步说明了地震动大量不确定性的存在[6-7]．

统计分析中巨大的离散性一直是影响设计谱精确估计的重要因素．地震动加速度反应谱离散性偏大的区段主要集中于长周期部分[8-9]．尽管长周期地震作用问题已越来越引起关注[10-15]，但现行建筑抗震规范中设计谱，尤其长周期段的斜直线表达尚存在许多值得商榷的问题．为了进一步探讨大地震地震动的特性，笔者采用了一种新的地震动反应谱研究方法，在建立了一个综合强地震动数据库的基础上，考虑地震动反应谱的特征将强震记录分为2类，即普通型地震动和低频型地震动；采用数字滤波方法先将低频型地震动中的长周期分量分离，再分析滤波后的低频型地震动与普通型地震动反应谱的特征；通过引入简谐地震动模型来等效所分离的低频分量，并讨论低频型地震动、所分离获得的低频分量与高、中频分量参数间的关系；最后为设计谱的标定及表达提出改进建议，以期能为设计谱的精确标定提供新的参考方法和依据．

1 地震动数据库

建立了一个包含220条水平方向记录的强地震动数据库．地震动为近期世界范围内11次M6～9级地震中获取的自由场地的数字式记录，地震信息见表1. 主要来源于美国强震动数据库(http：//www. strongmotioncenter.org/和http：//peer.berkeley.edu/)，汶川地震记录选自国家强震观测中心数据库(NSMONS).在选取地震动时所遵循的原则是：为减小单次地震样本数引起的统计偏差，每次地震选取10个台站的20条水平记录；另外，为减小可能存在的近断层作用的影响，当震级大于M7时记录的断层距不小于40,km；在选取地震记录时考虑了地震动峰值因素，未调整前的加速度时程峰值在0.05,g～1,g之间，震中距不大于300,km；对所选强震记录采用统一的调零和滤波处理，滤波带宽范围均不小于0.05～25,Hz，以确保其较高的信噪比．

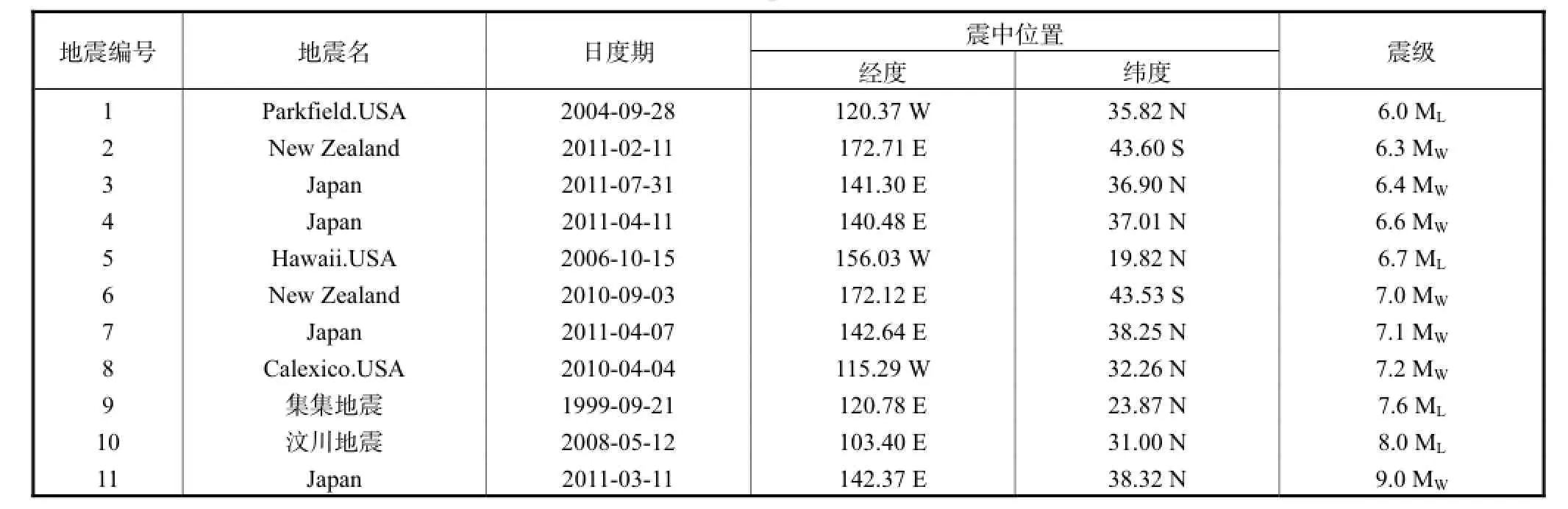
表1 地震信息表Tab.1 Earthquake information

所选的110个台站中，60个位于土层场地，8个位于岩石场地，其余台站的场地信息不详，各台站震中距和震级的分布如图1所示．由于本文中侧重于地震动分析方法的研究，选取记录过程中未考虑场地等因素的影响．

图1 地震动台站的震级与距离分布Fig.1Distribution of the ground motion stations in terms of magnitude and distance

2 地震动分类

离散性是影响地震动统计分析结果可靠性的重要因素．通过计算记录的规准加速度反应谱的变异系数(1组地震动规准反应谱的标准差曲线与平均谱之比)来表征地震动的离散程度．首先计算了全部220条地震动反应谱的变异系数曲线(见图2)，可以看出地震动加速度规准反应谱的离散性很大，并且主要表现在长周期段，大于5,s处的值均超过了1.5．为专门分析反应谱长周期段的特征，根据各地震动是否包含明显的低频分量将所选地震动分成2类：普通型(ordinary type，OT)和低频型(low frequency type，LFT)．分类时认为低频型地震动须满足2个基本条件：①加速度反应谱呈多峰状；②大于2,s长周期段出现的某谱峰值与加速度谱峰值的比值不小于10%．据此共筛选出25条低频型地震动，低频型地震动信息如表2所示，表2中：PGA为峰值地面加速度(peak ground acceleration)；PGV为峰值地面速度(peak ground velocity)；PGD为峰值地面位移(peak ground displacement)．其余195条记录为普通型地震动．

图2 地震动规准加速度反应谱变异系数曲线Fig.2Variation coefficient curves of the ground motion normalized acceleration response spectra

分别计算了普通型和低频型地震动的加速度规准反应谱变异系数曲线，见图2．从图2中可知，经分类后不论是普通型地震动还是低频型地震动，其规准加速度谱变异系数曲线在长周期段的值都明显减小．由此来看，地震动的分类统计必须考虑反应谱的曲线特征和长周期分量的影响．

地震动的幅值(A、V、D)及其比值(V/A、D/V)是反映地震动特征的重要参数[10]．分析表明，同一次地震中，低频型地震动的平均加速度幅值要小于普通型地震动，但其V/A、D/V明显大于普通型地震动见表3．因此可以把V/A作为区分地震动类型的一个基本参数．对2类地震动平均规准反应谱的比较见图3，图3中SA为谱加速度．由图3可知，2类地震动反应谱的差异十分明显，普通型地震动规准反应谱的谱值在4,s处已减小为谱峰值的5%，而低频型地震动的谱值则为峰值的35%；在短周期段低频型地震动的反应谱值相对较小，谱峰值右移趋势明显．

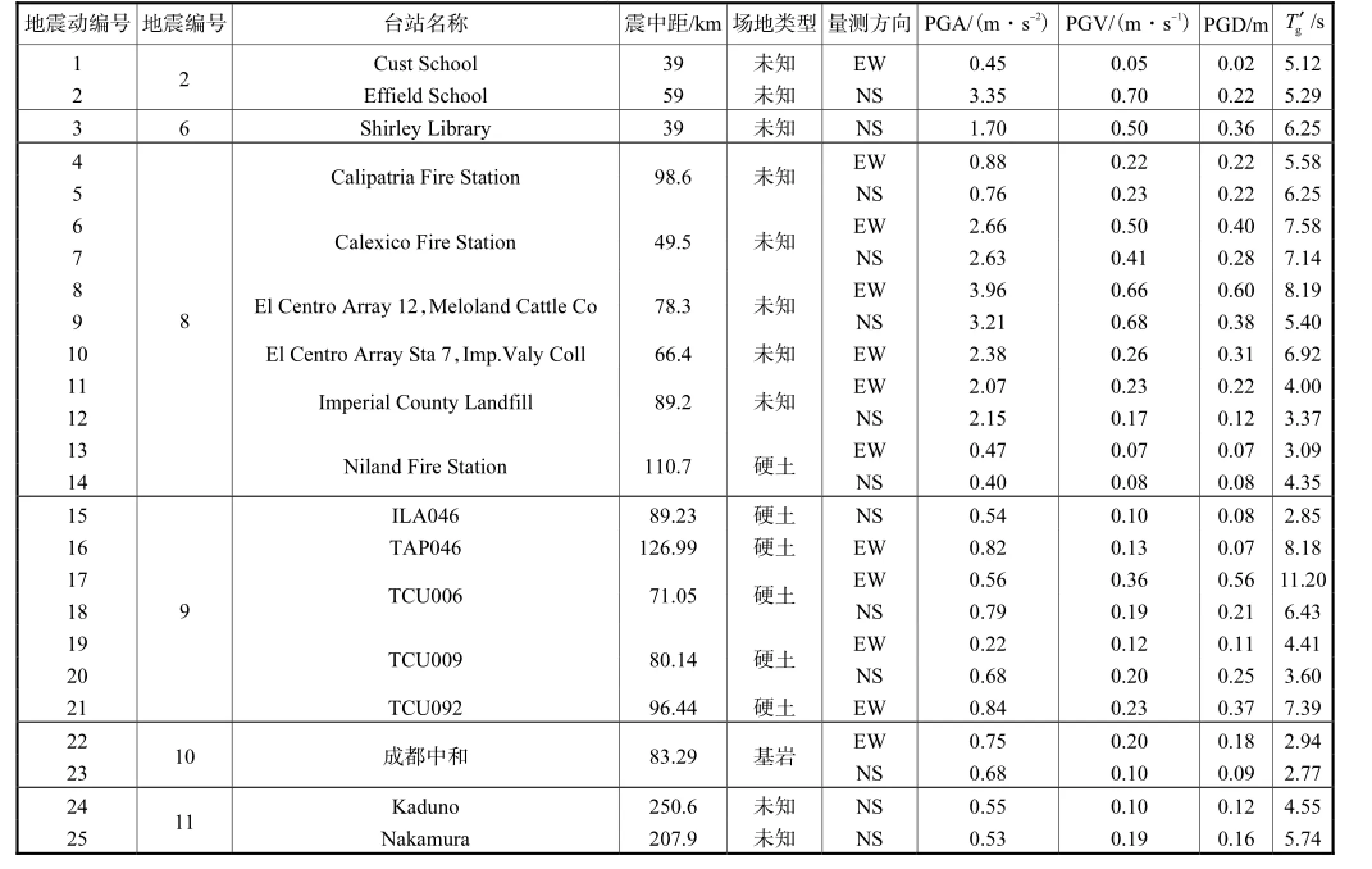
表2 低频型地震动信息Tab.2 LFT ground motion information

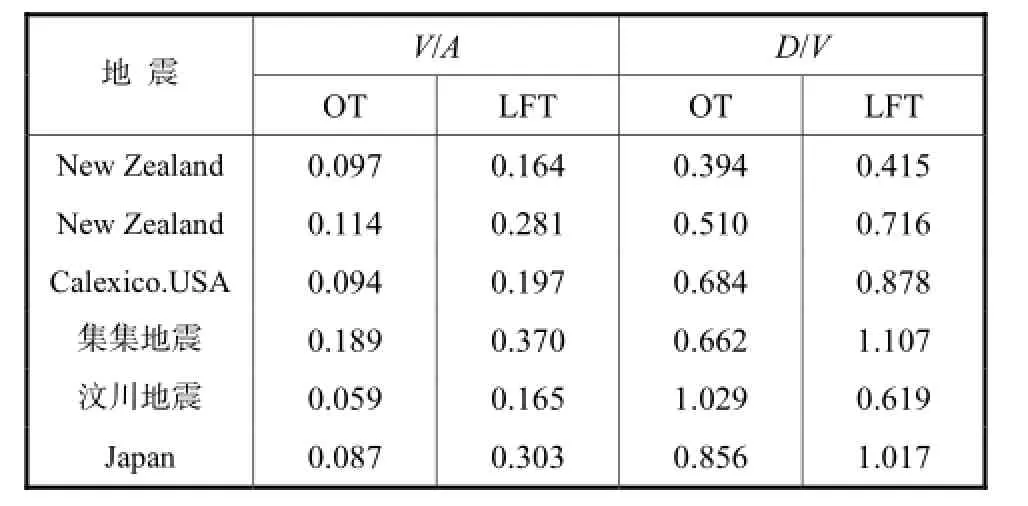
表3 2类地震动的幅值比Tab.3 Amplitude ratios of two types of ground motions

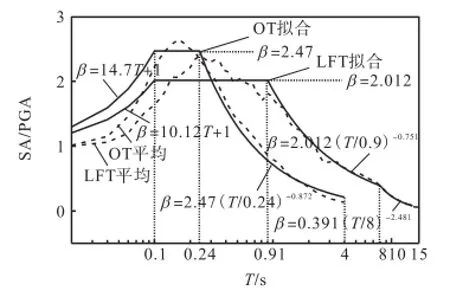
图3 平均加速度反应谱及拟合曲线Fig.3 Averaged acceleration normalized response spectra and the fitting curves

3 地震动的分解与参数分析

3.1 地震动分解方法

低频型地震动区别于普通型地震动的重要标识是含有明显的低频分量．为进一步探讨低频型地震动的参数特征，采用数字滤波方法对低频型地震动进行分解，将其分解为低频分量(low frequency components，LFC)和高、中频分量(high and median frequency components，HMFC)．目前采用分量分离方法进行地震动特征分析的研究甚少．Baker[16]和Ghahari等[17]曾分别尝试采用小波分析理论和“移动平均值”的方法针对近断层地震动进行分解，并讨论其低频成分的特性．但Ghahari等[17]分析指出，采用小波方法得到的分解地震动不能较好地反映实际地震动各组成分量的特征．基于以上考虑，本文中采用了数字滤波方法进行地震动的分解．数字滤波采取高通或低通的滤波方式便可以精确地提取原始地震动中的低频成分，实现对地震动的分解．

分析中采用Seismo Signal滤波软件进行低频型地震动的分量分离处理．为衡量分解前后地震动反应谱的变化程度，定义一个参数k，即

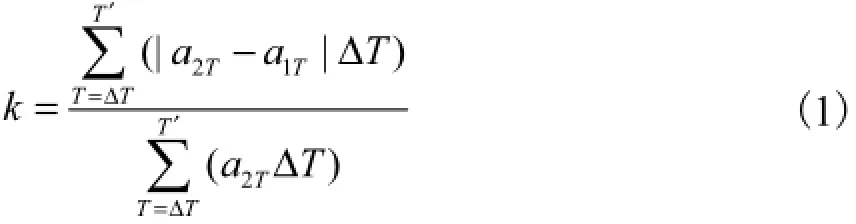
其中：1Ta为原始地震动加速度反应谱在周期T时的谱值；2Ta为地震动分解后又重新组合的地震动加速度反应谱在周期T时的谱值；TΔ为反应谱计算采用的时间步长；T′为反应谱计算周期总长．式(1)的物理意义就是分解后重新叠加组合的地震动反应谱相对原始地震动反应谱的改变量，k值越小表明分解前后反应谱的吻合程度越高，也即分解与组合地震动之间的变化越小，藉此来验证所采用的分解方法的有效性．

滤波频率是在分解时需要确定的一个重要参数．参考低频型地震动的选取原则，采用地震动加速度反应谱长周期段明显的谱谷对应频率作为滤波控制频率．经对25条低频型地震动分解，求得其平均的k值约为0.05．文中以5号地震动(Calexico Earthquake，Calipatria Fire Station，NS)和21号地震动(Chi-Chi Earthquake，TCU092 Station，EW)为例说明分解地震动反应谱的变化情况，见图4，图中SV和SD分别为谱速度和谱位移．可以看出，由分解得到的HMFC和LFC能够很好地反映原始地震动中、短周期和长周期段的特征．图3中HMFC和LFC谱曲线的交点频率恰是滤波所采用的控制频率．

3.2 地震动参数分析

为了深入了解所分解分量与低频型地震动的参数关系，对分解分量的时程和一些参数进行了分析．表4分别给出了高、中频分量(HMFC)、低频分量(LFC)与低频型(LFT)地震动的幅值关系．可以看出，HMFC的加速度幅值A与LFT的A的比值以及LFC的位移幅值D与LFT的D的比值均接近1；而对于速度幅值V的比值，LFC比HMFC对应的值稍高．因此，对于LFT地震动，其加速度时程主要由HMFC控制，其速度和位移时程则主要由LFC控制．这与文献[10]中关于类谐和地震动的速度和位移幅值取决于类谐和振动阶段的说法是基本一致的.

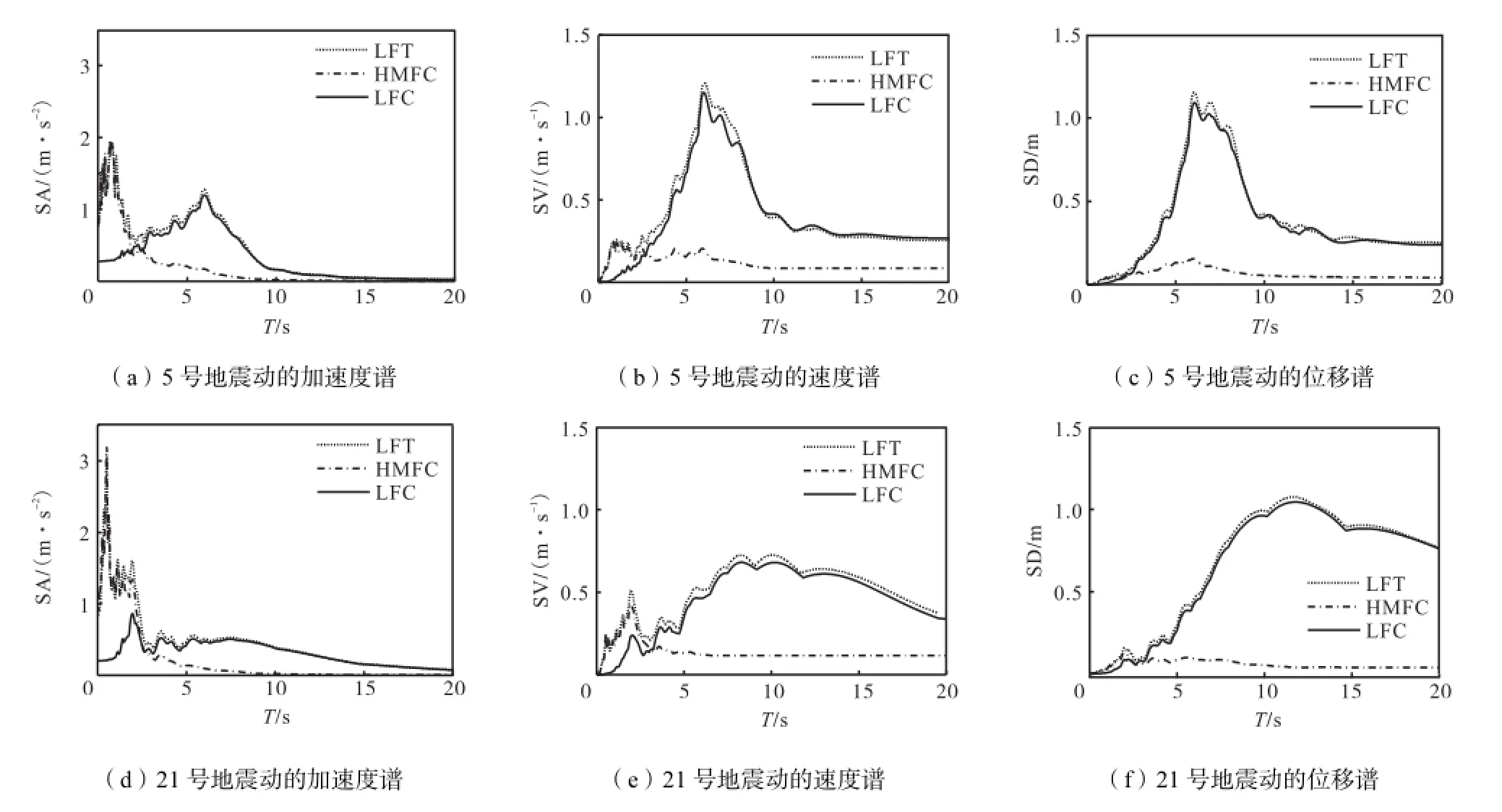
图4 分解地震动反应谱Fig.4 Decomposed ground motion response spectra

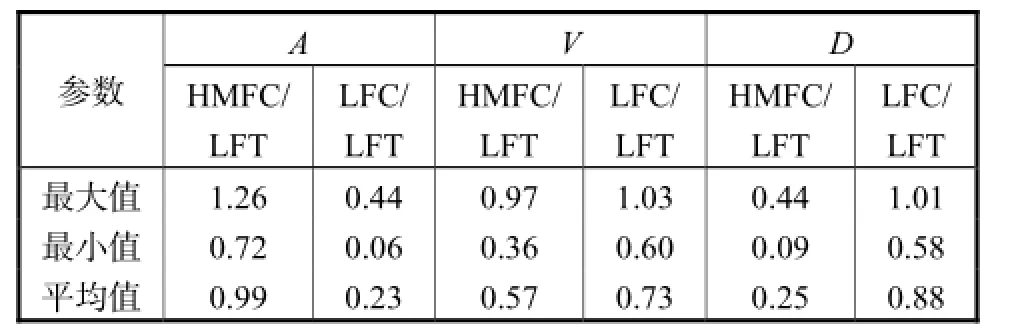
表4 3种地震动(LFT、HMFC、LFC)的幅值A、V、D之间的比值Tab.4 Ratios between A、V、D of ground motions (LFT、HMFC、LFC)

对分解分量时程峰值出现的时刻进行了相关性分析，把3种地震动(LFT、HMFC、LFC)的加速度、速度和位移时程峰值时刻分别记为tA、tV、tD，tHMA、tHMV、tHMD和tLA、tLV、tLD．分析发现，tHMA与tA，tLD与tD均表现出明显的相关性；tLV与tV的相关性更强(见图5)．

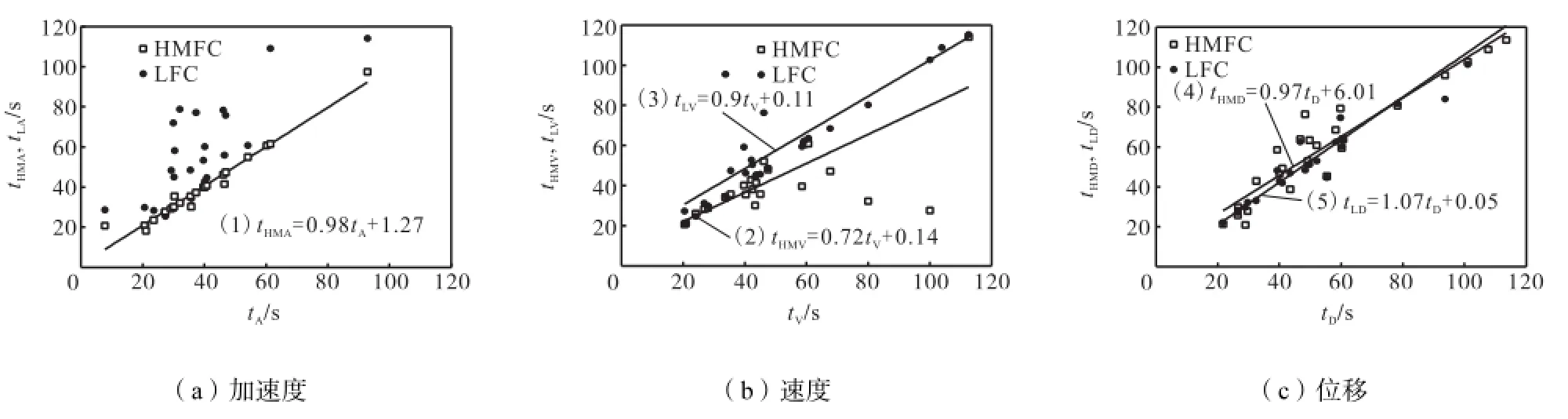
图5 时程峰值相关图Fig.5 Correlation diagram of time-history peak values

3.3 低频分量的等效

从所分离的低频分量来看，其组成较为简单，可以认为是由少数几个简单的简谐分量组成．为了探讨低频分量的特征，引入了一种用于等效低频分量的两阶段平稳简谐波模型，其加速度、速度和位移时程

可表示为

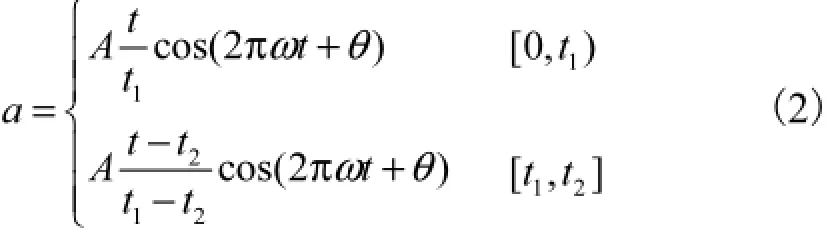
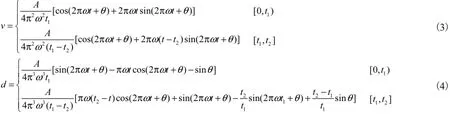
式中：t1为峰值时刻，s；t2为时程总长，s；A为加速度幅值，g；ω为自然频率；θ为初始相位角，rad．速度表达式中没有常数项，所以位移时程是围绕x轴波动的，需要满足的条件为cos(2,πωt1+θ)=0，cos (2,πωt2+θ)=0．

根据各低频分量的特点选取相应参数的模型地震动去等效真实的低频分量，当选取的模型数多于1时考虑模型地震动的组合方式，选取反应谱吻合程度最高的1条作为此低频分量地震动的等效地震动．计算表明，25条LFC分量中有18条仅需要1个简谐波模型即可实现较好的模拟和等效，有5条需要2个简谐波模型进行组合去等效，有2条需要3个简谐波模型以实现其等效．仍然以5号和21号地震动为例，图6给出了其低频分量与等效地震动(equivalent ground motion，EGM)反应谱的对比．可以看出，不论是加速度、速度还是位移反应谱都能够使用简谐分量模型较好地实现低频分量的等效．

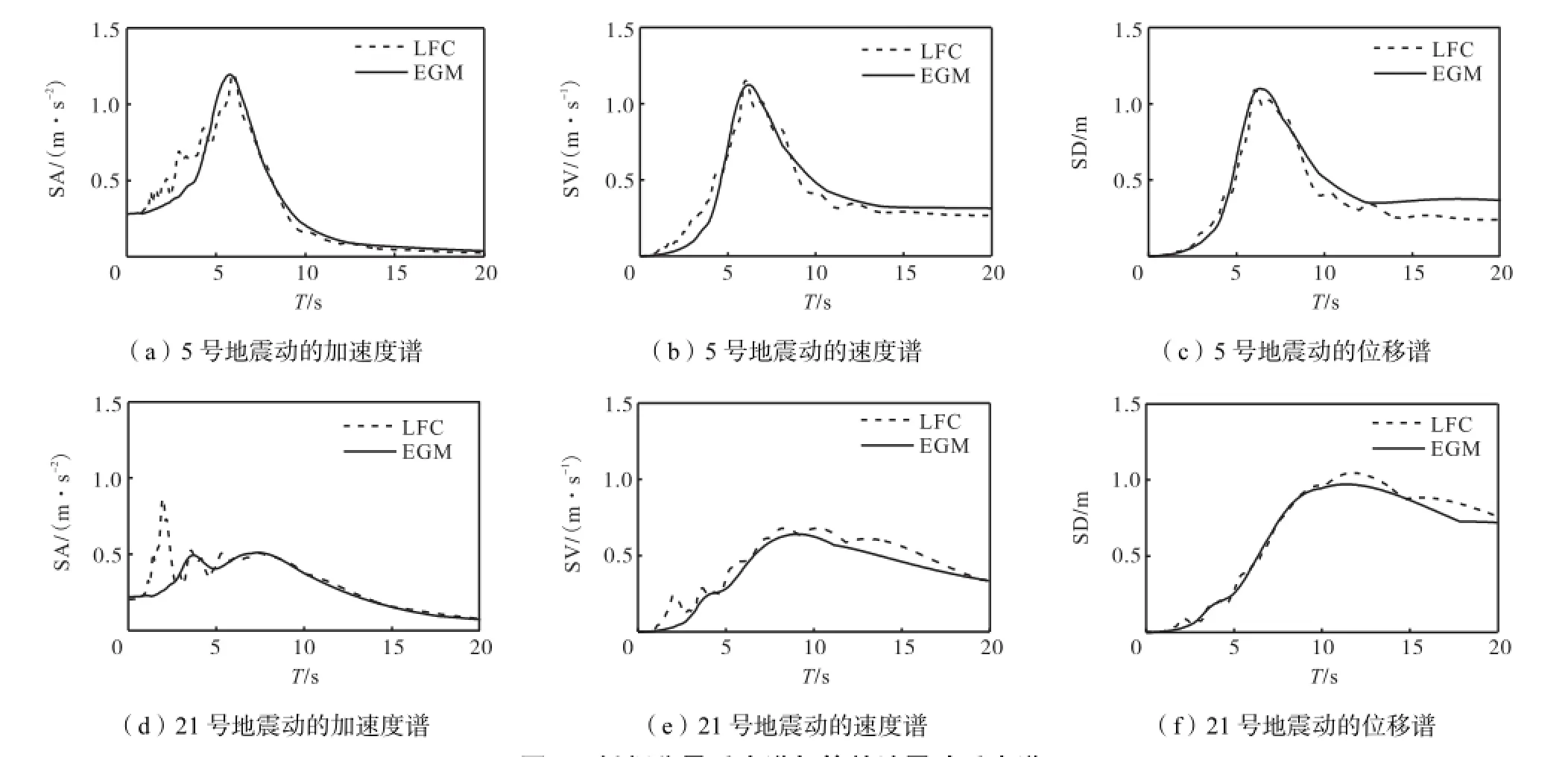
图6 低频分量反应谱与等效地震动反应谱Fig.6 LFC response spectra and the equivalent ground motion spectra

4 设计谱的标定

我国《建筑抗震设计规范》[18]所采用的设计谱在长周期段的取值相对于低频型地震动反应谱的取值偏低[19]，而相对于普通型地震动反应谱的取值明显偏高，且长周期段斜直线衰减形式不能够反映地震动反应谱的基本变化规律[20]，一个重要的原因在于设计谱的标定未能够考虑地震动的特征并加以区别对待，仅采用一种固定形式的设计谱不可能实现长周期段的合理表达．

对于普通型地震动反应谱，其谱值在3,s处已减小到较小的谱值，因此，其设计谱长周期段的表达可以直接将平均谱进行拟合，在下降段采用一次指数衰减的形式，如图3所示．对于低频型地震动，若采用平均谱直接标定设计谱显然是不合适的．为了能够实现低频型地震动长周期段的合理表达，本文提出了一种在对低频型地震动分解基础上，通过对长周期段谱值进行修正进而实现低频型地震动设计谱表达的方法．

由于双规准反应谱比通常的规准反应谱更能反映地震动反应谱的一致性[21]．针对所分解得到的25条低频分量的加速度反应谱进行了双规准化处理，见图7．为进一步获得平滑、简单的反应谱曲线，并体现低频分量反应谱的主要特征，又计算了25条低频分量的等效地震动对应的双规准加速度反应谱，如图8所示．分析发现等效地震动的双规准反应谱大致可以分为2组：曲线组1和曲线组2．再针对2组谱曲线的平均谱进行简化处理，可以得到2条拟合标准曲线S1、S2，见图9．2条标准曲线的差异主要是与低频分量的循环周期数有关[10]，较为扁平的曲线S1对应低频分量的循环数相对小于S2．标准曲线S1、S2的表达式分别为

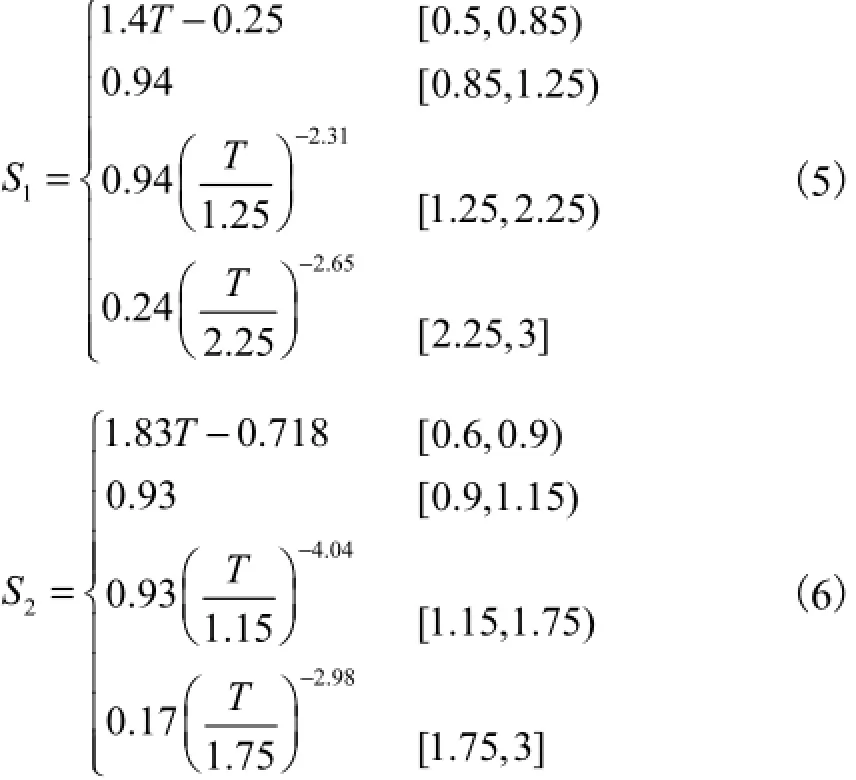
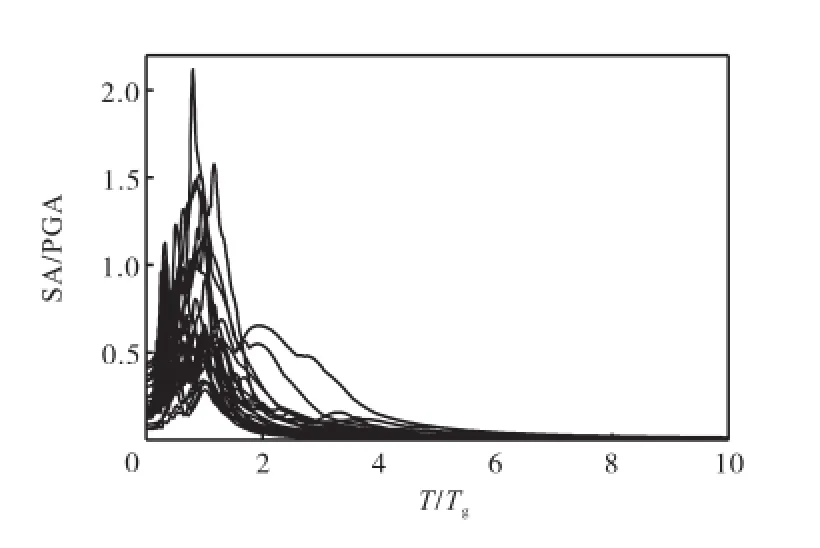
图7 低频分量地震动双规准反应谱Fig.7 Bi-normalized response spectra of LFC ground motion

低频型地震动的反应谱在长周期段明显出现1个谱峰．因此，低频型地震动对应的设计谱理论上应该有2个特征周期，分别分布在短、长周期段．对应于短周期段的特征周期记为第一卓越周期gT，对应于长周期段的特征周期可记为第二卓越周期gT′．通过对低频分量反应谱的标定，确定了25条低频型地震动分别对应的第二卓越周期gT′值，见表2．

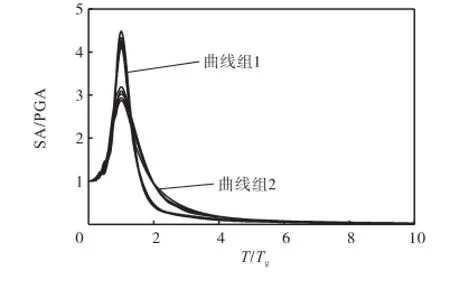
图8 等效地震动双规准反应谱Fig.8 Bi-normalized response spectra of EGM

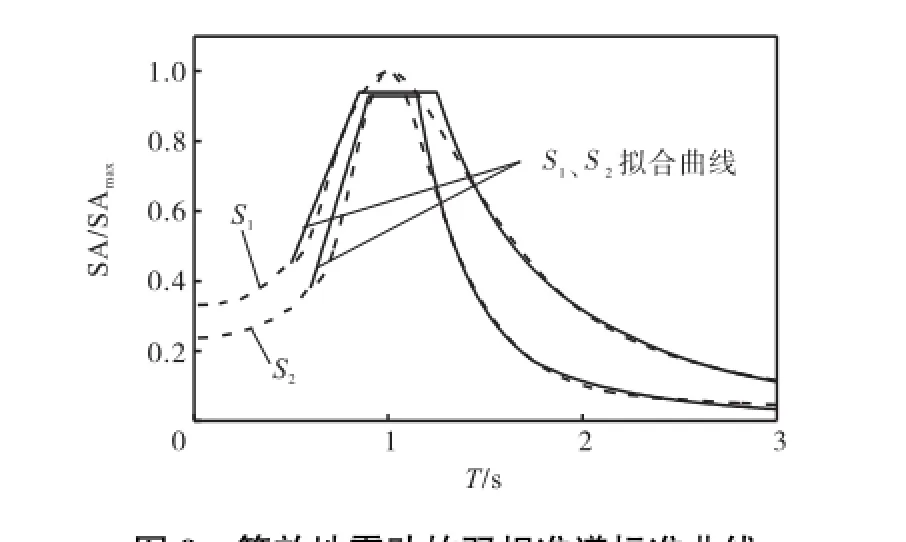
图9 等效地震动的双规准谱标准曲线Fig.9Standard curves of bi-normalized response spectra of EGM

进一步分析表明，低频分量的加速度反应谱峰值约为高频分量地震动反应谱峰值的1/2．因此，低频型地震动设计谱可以在所分离得到的高频分量反应谱的基础上附加一0.5倍高度、展开在第二卓越周期的标准谱曲线．图10所示为展开在第二卓越周期为8,s处的低频型地震动设计谱．这种设计谱的建立方法主要有2个优点：①能够同时体现低频型地震动反应谱长、短周期段的基本特征；②采用等效地震动进行标定使设计谱的表达简单、应用方便，且灵活性强．

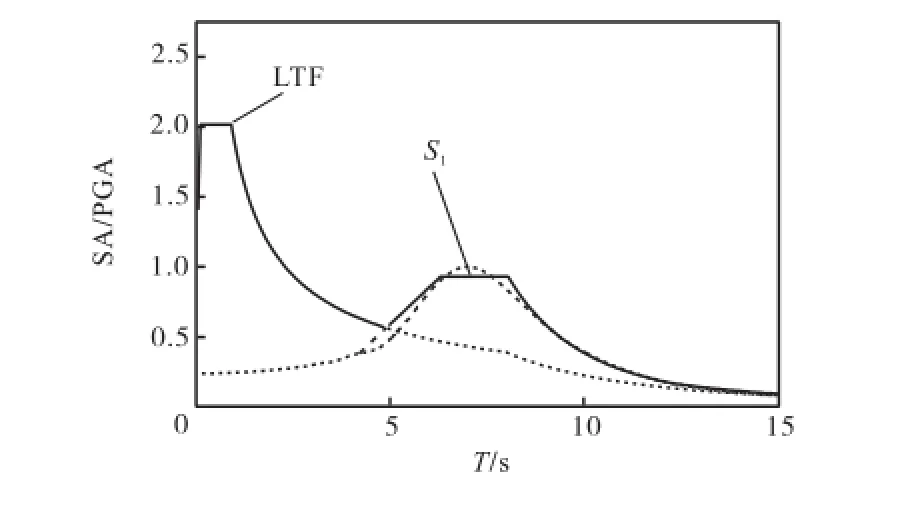
图10 低频型地震动设计谱Fig.10 Design spectrum of LFT ground motion

5 结 论

(1) 按照地震动是否包含明显的长周期分量可以将地震动分为普通型和低频型两类，分类之后的地震动反应谱的离散性均明显降低．地震动反应谱的特征分析和设计谱标定应充分考虑长周期分量的影响并加以区别对待．

(2) 相对于普通型地震动，低频型地震动的加速度幅值A较小，但其幅值比V/A、D/V均较大．2类地震动反应谱不仅在长周期段差异明显，短周期段也存在较大区别，低频型地震动反应谱的峰值周期明显右移．

(3) 数字滤波方法能够很好地将低频型地震动分解成高、中频分量和低频分量．低频型地震动时程的加速度幅值主要受高频分量控制，其速度和位移幅值主要取决于低频分量；高、中频分量、低频分量以及低频型地震动之间的时程峰值出现的时刻具有较明显的相关性；低频分量反应谱的离散性较大，但其频率组成简单，可以采用简谐地震动进行较好的等效.

(4) 普通型地震动的设计谱可根据平均谱的特征直接标定．低频型地震动设计谱的确定可分为两步进行：先针对其分离的高、中频分量进行设计谱的标定，再针对低频分量采用简谐波等效和附加长周期设计谱的方法加以确定．

(5) 本文中分析指出设计谱的标定必须考虑地震动长周期分量的影响，提出了采用分量分离方法进行地震动反应谱分析的新方法，为地震动的分类和设计谱的标定及其合理表达提供了参考依据．但低频型地震作用设计谱的建立仍然存在许多值得进一步探讨的问题，如低频型和普通型地震动的分类原则与方法，低频型地震动分解后低频分量与高频分量反应谱卓越周期、谱高度之间关系的确定等，限于篇幅，相关工作将另文讨论．

［1］ 胡聿贤. 地震工程学[M]. 北京：地震出版社，2006.

Hu Yuxian. Earthquake Engineering [M]. Beijing：Earthquake Press，2006（in Chinese).

［2］ 徐龙军，谢礼立，胡进军. 抗震设计谱的发展及相关问题综述[J]. 世界地震工程，2007，23(2)：46-57.

Xu Longjun，Xie Lili，Hu Jinjun. The review of development and certain problems in seismic design spectra[J]. World Earthquake Engineering，2007，23(2)：46-57(in Chinese).

［3］ Seed H B，Ugas C，Lysmer J. Site-dependent spectra for earthquake-resistance design[J]. Bull Seism Soc Am，1976，66(1)：221-243.

［4］ Tehranizadeh M，Hamedi F. Influence of earthquake source parameters and damping on elastic response spectra for Iranian earthquakes[J]. Engineering Structures，2002，24(7)：933-943.

［5］ 周雍年. 震级、震中距和场地条件对地面运动反应谱的影响[J]. 地震工程与工程振动，1984，4(4)：14-21.

Zhou Yongnian. The influences of magnitude，epicenter and site conditions on ground motion response spectra [J]. Earthquake Engineering and Engineering Vibration，1984，4(4)：14-21(in Chinese).

［6］ Wang G Q，Zhou X Y，Zhang P Z，et al. Characteristics of amplitude and during for near fault strong ground motion from the 1999 Chi-Chi，Taiwan earthquake[J]. Soil Dynamics and Earthquake Engineering，2002，22(1)：73-96.

［7］ Li Xiaojun，Zhou Zhenghua，Yu Haiyin，et al. Strong motion observations and recordings from the great Wenchuan earthquake[J]. Earthquake Engineering and Engineering Vibration，2008，7(3)：235-246.

［8］ Beck J L，Hall J F. Factors contributing to the catastrophe in Mexico City during the earthquake of September 19，1985 [J]. Geophys Res Lett，1986，13(6)：593-596

［9］ Koketsu K，Hatayama K，Furumura T，et al. Damaging long-period ground motions from the 2003 Mw8.3 Tokachi-oki，Japan，earthquake [J]. Seismol Res Lett，2005，76：67-73.

［10］ 徐龙军，胡进军，谢礼立. 特殊长周期地震动的参数特征研究[J]. 地震工程与工程振动，2008，28(6)：20-27.

Xu Longjun，Hu Jinjun，Xie Lili. On characteristics of ground motion parameters for special long-period ground motions[J]. Earthquake Engineering and Engineering Vibration，2008，28(6)：20-27(in Chinese).

［11］ 李春锋，张 旸，赵金宝，等. 台湾集集大地震及其余震的长周期地震动特性[J]. 地震学报，2006，28(4)：417-428.

Li Chunfeng，Zhang Yang，Zhao Jinbao，et al. Longperiod ground motion characteristics of the 1999 Chi-Chi，Taiwan，mainshock and aftershocks[J]. Acta Seismological Sinica，2006，28(4)：417-428(in Chinese).

［12］ 吴 迪，罗奇峰，罗永峰. 长周期地震波的研究进展[J]. 地震研究，2007，30(3)：296-302.

Wu Di，Luo Qifeng，Luo Yongfeng. Development oflong-period seismic wave research[J]. Journal of Seismological Research，2007，30(3)：296-302(in Chinese).

［13］ 俞言祥. 长周期地震动研究综述[J]. 国际地震动态，2004，30(7)：1-5.

Yu Yanxiang. Review of long-period ground motion study[J]. Recent Developments in World Seismology，2004，30（7)：1-5(in Chinese).

［14］ 谢礼立，周雍年，胡成祥，等. 地震动反应谱的长周期特性[J]. 地震工程与工程振动，1990，10(1)：1-19.

Xie Lili，Zhou Yongnian，Hu Chengxiang，et al. Ground motion response spectrum’s long-period characteristics [J]. Earthquake Engineering and Engineering Vibration，1990，10(1)：1-19(in Chinese).

［15］ Ruiz S，Saragoni G R. Free vibration of soils during large earthquakes[J]. Soil Dynamics and Earthquake Engineering，2009，29：1-16.

［16］ Baker J W. Quantitative classif i cation of near-fault ground motions using wavelet analysis[J]. Bulletin of Seismological Society of America，2007，97(5)：1486-1501.

［17］ Ghahari S F，Jahankhah H，Ghannad M A. Study on elastic response of structures to near-fault ground motions through record decomposition[J]. Soil Dynamics and Earthquake Engineering，2010，30(7)：536-546.

［18］ 中华人民共和国标准. GB50011—2001 建筑抗震设计规范[S]. 北京：中国建筑工业出版社，2001.

The Standard of the People's Republic of China. GB50011—2001 Code for Seismic Design of Buildings[S]. Beijing：China Architecture and Building Press，2001(in Chinese).

［19］ 周雍年，周正华，于海英. 设计反应谱长周期区段的研究[J]. 地震工程与工程振动，2004，24(2)：15-18.

Zhou Yongnian，Zhou Zhenghua，Yu Haiying. A study on long period portion of design spectra[J]. Earthquake Engineering and Engineering Vibration，2004，24 (2)：15-18(in Chinese).

［20］ 翁大根，徐植信. 对上海市抗震设计反应谱及时程曲线的认识[J]. 地震工程与工程振动，2001，21(1)：79-83.

Weng Dagen，Xu Zhixin. Understanding of seismic design spectrum for Shanghai[J]. Earthquake Engineering and Engineering Vibration，2001，21(1)：79-83(in Chinese).

［21］ 徐龙军，谢礼立. 场地相关双规准化地震动加速度反应谱[J]. 哈尔滨工业大学学报，2004，36(8)：1061-1064.

Xu Longjun，Xie Lili. Site-dependent bi-normalized earthquake acceleration response spectra[J]. Journal of Harbin Institute of Technology，2004，36（8)：1061-1064(in Chinese).

Ground Motion Response Spectra Through Component Decomposition Method

Xu Longjun，Zhao Guochen，Xie Lili
(Department of Civil Engineering，Harbin Institute of Technology at Weihai，Weihai 264209，China)

The large discreteness has been the key factor affecting the accurate estimation of design spectra in the statistical analysis of ground motion response spectrum. Long-period portion in ground motion response spectrum usually exhibit larger discreteness. To further study the response spectrum and its long-period characteristics，a comprehensive strong ground motion database was established. The strong motion records were divided into two categories，ordinary type and low-frequency type，by considering the characteristics of ground motion response spectrum；the digital filtering method was adopted to separate the long-period component from the low frequency type motions；then，a two-stage smooth harmonic model was introduced to simulate the separated component. Results show that response spectral characteristics of the filtered low frequency type motions are still very different from those of the ordinary type；there are some correlations in between low frequency motions，low frequency components and the filtered high and median frequency components. It is stressed that the design spectra of ordinary type ground motion and low frequency ground type motion must be calibrated separately. For ordinary motions，design spectra can be constructed by using the average spectra，while for low frequency motions design spectra can be obtained by modifying the spectra of the long period. The study not only provides a new approach to the analysis of response spectrum，but also is helpful in the precise calibrating of design spectra.

ground motion；harmonic ground motion；ground motion decomposition；seismic design spectrum

P315.9

A

0493-2137(2013)11-1003-09

DOI 10.11784/tdxb20131109

2012-09-21；

2013-05-11.

国家自然科学基金资助项目(51178152，51238012)；科技部地震行业科研专项资助项目(201208013)；中国博士后基金资助项目(111168).

徐龙军（1976— ），男，博士，副教授.

徐龙军，xulongjun80@163.com.