双锥流量传感器的数值模拟与优化设计

徐 英，安俊达，龙征海，高 璐

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津市过程检测与控制重点实验室，天津 300072；3. 中国石油西南油气田公司川中油气矿，成都610051)

双锥流量传感器的数值模拟与优化设计

徐 英1,2，安俊达1,2，龙征海3，高 璐1,2

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津市过程检测与控制重点实验室，天津 300072；3. 中国石油西南油气田公司川中油气矿，成都610051)

以数值仿真和实验两方面研究了一种新型的双锥流量传感器，考察了该传感器的关键几何参数即前锥角、后锥角、等效直径比及槽道长度对流出系数、线性度及相对压力损失等性能指标的影响，并预测得到了1个最优模型进行实流实验标定．采用正交实验法进行CFD数值模拟．分析结果表明：前锥角对双锥流量传感器相对压力损失、流出系数及流出系数线性度有重要的影响；后锥角则对相对压力损失有重要影响．最终实流实验验证结果与仿真计算结果具有良好的吻合度．

双锥流量传感器；正交实验法；流出系数；线性度；相对压力损失

20世纪80年代中期，美国McCro-meter公司推出了一种新型锥体差压式流量传感器，不同于传统的流量传感器在管道中添加阻挡物强迫流体迅速收缩到管道中心轴线附近的设计思路[1]，它采用了同轴安装在管道中的V形尖圆锥将流体逐渐节流收缩到管道内边壁的设计结构，并通过测量此锥体前后的压力差实现流量测量．从理论上来讲，该结构很好地保持了流动的稳定性，减弱了压力波动的幅值，产生的压差信号更加稳定，信噪比更高．经过近年来的使用证明，V锥流量传感器与孔板等传统的流量传感器相比，具有压力损失小、前后直管段短、抗脏污等优点，尤其是在一些特殊的应用场合，如城市燃气测量、垃圾焚烧发电、高炉煤气及煤层气测量等领域具有明显优势[2]，因此，近年来V锥流量传感器已成为国内外节流式流量传感器的研究热点[3-4]．

笔者所描述的双锥流量传感器以近年来流行的V锥传感器结构为基础进行设计，芯体同样安装于圆形管道中心，可实现流体边壁收缩，不同之处在于该芯体由前后2个锥体以及连接槽道3部分构成．目前，国内外已有部分学者对此类流量传感器的测量性能进行了一定的仿真及实验研究，但对于构成双锥流量传感器的各几何参数对其综合测量性能影响的研究鲜有报道．为此，笔者针对100,mm口径、前锥角为45°/60°/90°、后锥角为30°/45°/60°、槽道长度为5,mm/ 10,mm/15,mm/25,mm、等效直径比为0.55/0.65/0.75的双锥流量传感器模型，开展了基于正交化实验方法的CFD仿真研究，预测了双锥流量传感器几何参数及其最优匹配，并最终通过实流实验对优化样机进行了性能验证．

1 理论基础

1.1 双锥流量传感器的基本结构

双锥流量传感器的简化结构示意如图1所示，即在封闭的管流系统中同轴安装一节流体．图1(b)中：α 为前锥角；γ为后锥角；β 为等效直径比，即d/D；l为槽道长度；D为管道直径；P1、P2、P3分别为3处取压位置.

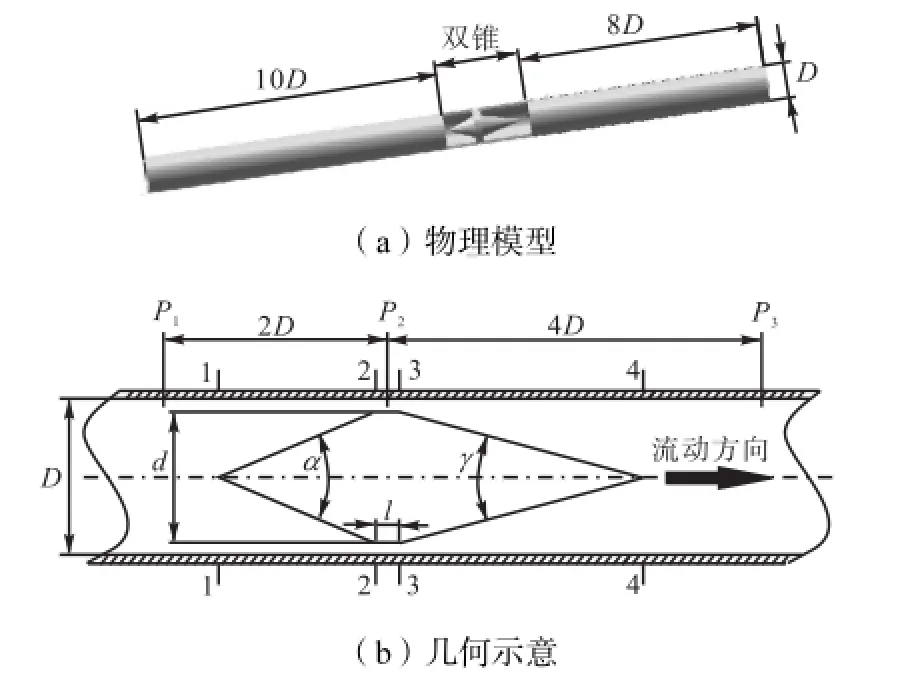
图1 双锥流量传感器结构示意Fig.1 Structure of the double-cone flowsensor

1.2 双锥流量传感器的测量性能参数

对节流式流量传感器而言，流出系数、线性度与相对压力损失是较为重要的性能参数，本研究以这3个性能参数为考察指标，研究构成双锥流量传感器的各几何参数对其测量性能的影响．1) 流出系数流出系数为实际流量与理论计算流量的比值，可由流体流量计算式导出，即

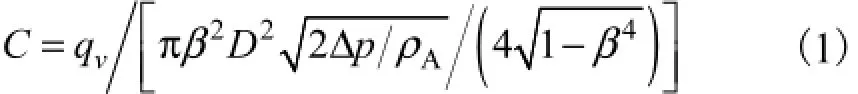
2) 线性度

定义每个流量点下的流出系数为Ci，流量计所有流量点下的平均流出系数为C，将流出系数线性度的计算式表示为

3) 相对压力损失

不同节流式流量传感器节能效果各不相同，本质上无一例外需要消耗一定的能量，并且耗能的大小与传感器的几何结构参数直接关联．在进行双锥流量传感器的研究时，采用流线型设计思想的目的是要最大程度地减小传感器的压力损失．本研究将相对压力损失作为重要考察指标之一，定义为

式中：Δω为永久压力损失；Δp为双锥传感器正常测量差压值．

永久压力损失是指由于流量传感器的安装所造成的额外压力损失，某一特定流量的永久压力损失计算式为

式中：Δp"为节流装置产生的压力损失(本文中为p1与p3之间的差压)；Δp'为管道沿程压力损失，按达西-维伊斯巴赫公式[5]计算，即

式中：L为直管段长度；ρ为流体密度；v为流体速度；λ为摩擦系数，无纲量，由阿里特舒利近似公式[5]求得，即

式中：Δ为相对粗糙度，取0.000,32；Re为雷诺数．

2 流场的数值模拟

2.1 正交实验设计

采用正交实验法代替遍历实验法优化实验分组，利用正交实验法本身所具有的均衡分散性与整齐可比性达到减少实验次数、提高实验效率以及均衡考虑各因素对考察指标影响的目的．从双锥节流装置的前锥角、后锥角、等效直径比和槽道长度这4个几何因素入手，每个因素取3个水平，建立相应的4因素3水平正交表L9(34)．因素水平与正交实验设计见表1和表2．

表1 因素水平表Tab.1 Levels and factors

表2 L9(34)正交实验表Tab.2 A standard L9(34)matrix

同时，对双锥流量传感器模型的4个影响因素型设计代号，即α-γ-β-l．例如，前锥角45°，后锥角30°，等效直径比0.65，槽道长度5,mm的双锥流量传感器模型代号为45-30-0.65-0.005，其他模型依此类推．

2.2 建模、网格剖分与湍流模型

2.2.1 建模与网格剖分

根据正交实验表，建立9组仿真实验模型．由于双锥流量传感器的锥体为旋转体，具有轴对称性，在进行数值模拟实验时，建立的模型为二维结构，并且计算域只选取一半．网格划分如图2所示．

图2 网格划分(模型45-30-0.65-0.005)Fig.2 Double-cone grid (Model 45-30-0.65-0.005)

在网格剖分方面，尽量采用了结构化网格，在靠近锥体的关键区域网格划分最紧密，越靠近管道两端，网格越稀疏，网格总数近似为1.54×105，关键区域网格总数为1.0×105．这样既减少了总体的网格数，缩短了仿真时间，同时也保证了网格的质量，避免由于临近单元体积或面积的快速变化而导致计算结果出现误差．

2.2.2 湍流模型

标准k-ε模型是目前使用最广泛的湍流模型，而经过模型适应性比较研究[6]，发现RNG k-ε模型在本实验中比标准模型有更好的精度，故仿真工作选用RNG k-ε模型．在近壁面区域采用标准壁面函数法进行处理．

采用有限体积法实现控制方程的离散化，采用SIMPLE算法求解离散方程．在离散格式方面，根据Gan等[7]的研究，对于不可压缩流体的差分格式采用QUICK格式最为精确．该格式是一种改进离散方程截差的方法，精度较高，但这种格式并非绝对收敛，对网格质量要求较高．本研究的仿真计算中，除压力项的离散采用二阶迎风格式外，其余各项离散均选用QUICK格式．

2.2.3 边界条件

仿真介质为水，温度293,K；入口条件设定为速度入口，速度设定为0.1,m/s、0.3,m/s、0.7,m/s、1.0,m/s、3.0,m/s、5.0,m/s和7.0,m/s；出口设定为压力出口；残差收敛精度设为10-5．

2.3 仿真结果场域分析

2.3.1 速度及压力场计算结果分析

为从机理上分析双锥流量传感器不同结构因素对流出系数、线性度以及相对压力损失这3个考察指标的影响，本研究提取仿真模型计算后的速度场矢量图与压力场等势图进行比对分析．由于本研究采用正交实验的设计方法，不同的实验模型之间最多只有一个因子相同而其他3个因子都各不相同，这给横向的比较带来了困难．这里只选择前锥角45°结构下的3个不同模型(模型45-30-0.65-0.005、45-45-0.55-0.010和45-60-0.75-0.025)在同一个流速点(7,m/s)下的速度场矢量图与压力场等势图加以显示和比较．图3和图4分别为3组仿真模型的速度场矢量图与压力场等势图对比．

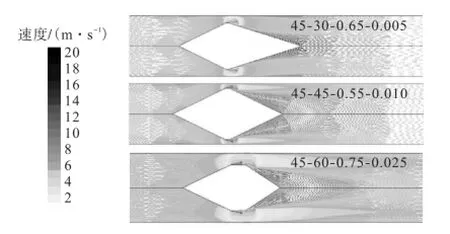
图3 3组模型的速度场矢量图对比Fig.3 Comparison of three velocity field vectors

从图3中可以看出，流体在流过锥体槽道部分时流速变化最大，并且该区域随着槽道长度的增加而增大；随着等效直径比的增加，管道近壁面速度变化的范围也在逐渐增大，这可由流体的伯努力方程与连续性方程解释．同时，流体在流经后锥角部分后有明显的流速滞流区与速度漩涡区的存在，这是因为流体在流经锥体槽道部分后仍保持较高的流速与较低的静压力，在流至后锥角部分时，流体流速逐渐减小，静压力回升，由于流体的黏性、局部阻力、静差压回流等引起了锥后的涡流．对比3个模型可知，虽然它们的等效直径比、槽道长、后锥角都各有不同，但可以直观地看到锥后流速滞流区与速度漩涡区的大小受后锥角变化的影响程度最大，随着后锥角的增大，该区域逐步变大．

图4 3组模型的压力场等势图对比Fig.4 Comparison of three pressure field contours

从图4中可以看出，流体在流过锥体时，压力大小的变化与流通面积的变化呈反比关系，并且锥体下游的压力均小于上游的压力，特别是在前后锥面与槽道面相交的地方，出现明显的低压力区，范围小但是有明显的叠加．对比3组模型发现，随着槽道长度的增加，低压力区在变大，叠加效果减弱．在锥后部分，由于后锥角的不同，流场压力值的大小不同，即随着后锥角的增大，节流锥体引起的压力损失增大，压力恢复所需的距离增大．

2.3.2 近壁面压力散点图分析

除了比对速度场矢量图与压力场等势图之外，本研究对比分析了同一流速下各结构在近壁面的静压力变化．图5为正交实验法构建的9组模型在1,m/s的流速下近壁面静压力变化曲线．

图5 近壁面静压力变化曲线(流速1,m/s)Fig.5 Change curve of the static pressure near wall (velocity 1,m/s)

从图5中可以看出：

(1) 在锥体前0.15,m位置流场相对稳定，流体流经锥体后，在0.4,m的位置达到相对稳定状态，即流场恢复．

(2) 在通过节流件前的静压力曲线中，1条曲线最高，其余曲线相差不大．最高的曲线模型为90-60-0.55-0.005，该模型的前锥角与后锥角均为最大，对流场的影响最大．

(3) 流体在通过节流件时，有明显的压降，并在槽道位置压降达到最大，这是由双锥流量传感器的节流体阻挡使得流通面积减小所致．同时，注意到流体在流经槽道后压力恢复所需要的距离不同，这与不同模型的槽道长度以及后锥角角度有关．对比9组模型发现，槽道区域压降的大小与等效直径比直接相关，等效直径比越小，静压力变化越剧烈；后锥角越大、槽道长度越长，静压力曲线就越平缓，静压力恢复所需距离越长．

2.4 正交实验极差分析与模型选优

2.4.1 正交实验的极差分析

为进一步准确得出前锥角、后锥角、等效直径比和槽道长度这4个因素对双锥节流装置流出系数、线性度以及相对压力损失的影响，采用极差分析方法，即计算正交实验表各列中各水平对应的考察指标平均值的最大值与最小值之差，并按照该差值从大到小的顺序进行排列，极差值越大、排名越靠前，则说明该因素对考察指标的影响越显著．本研究着重考察量程比1∶23(雷诺数下限30,000)和量程比1∶10 (雷诺数下限70,000)范围的计算结果，具体如表3～表5所示．

2.4.1.1 考察因素对不同考察指标的综合影响分析

从表3～表5中可以看出，各考察因素对考察指标的影响有一定的规律性，但在不同量程比范围内又略有不同，具体如下．

1) 流出系数

前锥角是影响流出系数最为显著的因素，并从极差数值的对比上可以看出前锥角对流出系数的变化起着决定性的作用；槽道长度对流出系数影响最小；后锥角与等效直径比对流出系数的影响程度相近．

表3 流出系数的极差分析Tab.3 Range analysis of discharge coefficient

表4 流出系数线性度的极差分析Tab.4 Range analysis of discharge coefficient linearity

表5 相对压力损失的极差分析Tab.5 Range analysis of relative pressure loss

2) 流出系数线性度

从极差数值以及排序中可以看出，前锥角是影响流出系数线性度的主要因素，其他因素对该考察指标的影响与量程比范围密切相关．在1∶23的量程比范围内，后锥角极差值与前锥角极差值相当，可以认为后锥角与前锥角有着相近的作用，是影响流出系数线性度的主要因素，其次是槽道长度与等效直径比；在1∶10的量程比范围内，等效直径比与槽道长度对流出系数线性度的影响作用相近，而后锥角则对流出系数线性度的影响最小．

3) 相对压力损失

后锥角是影响相对压力损失最显著的因素，其次是前锥角，而槽道长度则是对相对压力损失影响最小的因素．

2.4.1.2 同一因素不同水平对考察指标的影响分析

对上面结论进行进一步分析，即分析单个因素在其水平变化时，它对流出系数、流出系数线性度和相对压力损失的影响，具体如下．

1) 前锥角

随着前锥角的增大，流出系数呈现一直减小的趋势，并且流出系数变化明显；流出系数线性度则呈先减小后增大的趋势；相对压力损失呈现一直增大的趋势．

2) 后锥角

随着后锥角的增大，流出系数呈现先增大后减小的趋势，但总体变化不大；流出系数线性度呈先减小后增大的趋势；相对压力损失呈一直增大的趋势，并且变化明显．

3) 等效直径比

随着等效直径比的增大，流出系数、相对压力损失一直减小；但流出系数线性度在不同的量程比范围内呈现的变化趋势不同：在1∶23量程比下流出系数线性度一直减小，但在1∶10量程比下流出系数线性度先减小后增大．

4) 槽道长度

随着槽道长度的增大，流出系数呈现一直增大的趋势；流出系数线性度均值呈现先减小后增大的趋势；但相对压力损失在不同的量程比范围内呈现的变化趋势不同：在1∶23量程比下相对压力损失先减小后增大，但在1∶10量程比下相对压力损失一直减小．同时通过观察表3～表5中数据可以看出，随着槽道长度的增长，流出系数线性度在第2水平(10,mm)与第3水平(25,mm)之间变化特别剧烈，而槽道长度也对流出系数线性度的影响较大，故本研究增加一个因素水平(15,mm)代替第1水平(5,mm)重新建立3个模型，即45-30-0.65-0.015、60-45-0.75-0.015与90-60-0.55-0.015 ，进行仿真实验研究，计算结果如表6所示．

表6 新槽道长度下流出系数线性度均值对比Tab.6Comparison of discharge coefficient linearity on new channel flow length

从表6可以看出，新建立的15,mm的槽道长度对于流出系数线性度有一定改善．

2.4.2 参数的最优匹配分析

前述的数据分析得出了不同因素及其各自水平对于双锥流量传感器流出系数、流出系数线性度以及相对压力损失的影响，为预测优选模型奠定了理论基础，可以得到如下结论：

(1) 前锥角对3个考察指标的影响都比较大，且前锥角为45°时，相比于其他两因子即60°与90°，具有相对较好的流出系数线性度以及更低的相对压力损失，并且前锥角的变化对流出系数的影响极为显著，故本研究认为优选模型的前锥角为45°．

(2) 后锥角的变化对相对压力损失的影响显著，且后锥角选取30°时，相比其他两因子即45°与60°，具有流出系数线性度好与相对压力损失最小的优势，故本研究认为优选模型的后锥角为30°．

(3) 等效直径比对流出系数与流出系数线性度有一定程度的影响，可以看出相对于差别不大的流出系数，等效直径比为0.65结构下的线性度要比其他两因子下的线性度更好．

(4) 根据前述分析可知，槽道长度为15,mm是较为理想的长度．

综上可知，最优模型应为前锥角45°，后锥角30°，等效直径比0.65，槽道长度15,mm．

3 实流实验方法与结果分析

3.1 实验装置

本研究是在天津大学电气与自动化工程学院水流量实验室完成的．为提高实验效率，实验方法采用了标准表法．装置流程如图6所示．

图6 实验装置示意Fig.6 Operation schematic diagram of experimental facility

水泵可连续将水池中的水打入水塔，通过水塔溢流稳压．标准表为高精度电磁流量计．标准表法水流量装置不确定度为0.2%．差压变送器采用3台横河EJA110A，精度为0.075%；为提高对4～20,mA信号的采样精度，A/D卡选用NI的16位USB-6210采集卡．

3.2 实验样机

根据前文给出的45-30-0.65-0.015优化模型，即前锥角45°，后锥角60°，等效直径比0.65，槽道长15,mm，制作了内径100,mm的双锥流量传感器样机，具体的实验装置如图7所示，流动方向从右至左．

图7 样机装配照片Fig.7 Picture of prototype devices

3.3 实验方案

对每种节流装置进行实验时均用2台变送器，覆盖更宽的测量范围，取压方法均为管壁取压，一台用于测量锥体前后的差压，另一台测永久压力损失．中心取压孔位于槽道中心正上方管壁处，上游取压孔距中心取压孔2D，下游取压孔距中心取压孔4D．考虑到差压变送器在测量小流量点时精度较低，故实流实验的流速点定为0.7,m/s、1.0,m/s、3.0,m/s、5.0,m/s和7.0,m/s．

3.4 实流实验与仿真对比分析

表7给出了模型45-60-0.65-0.015的实流实验数据与CFD仿真数据，实流实验与仿真计算的比对误差分别为

式中：δE为仿真结果与实流实验流出系数线性度的比对误差；δCFD表示仿真计算得到的流出系数线性度；δEXP表示实流实验得到的流出系数线性度；Eξ为仿真结果与实流实验相对压力损失的比对误差；ξCFD表示仿真计算得到的相对压力损失；ξEXP表示实流实验得到的相对压损失．

从表7中可以看出，在雷诺数相近的情况下，实流实验与仿真计算的流出系数线性度比对误差不超过0.4%，相对压力损失比对误差不超过1.2%，证明了仿真计算的正确性．

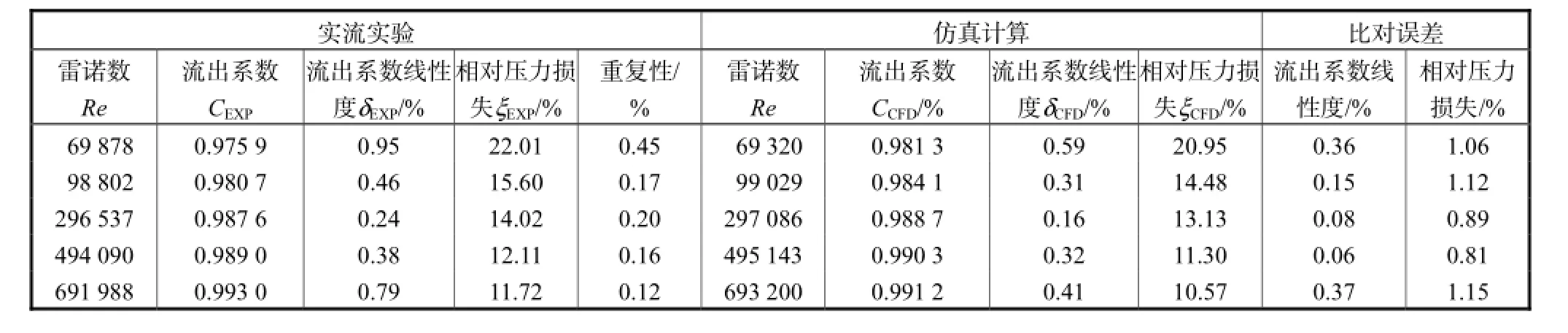
表7 45-30-0.65-0.015模型实物样机实流实验与仿真计算的数据对比Tab.7 Dada comparison between real flow experiment and numerical simulations of model 45-30-0.65-0.015

4 结 论

利用正交实验方法，通过对一种新型双锥流量传感器的CFD数值模拟，考察了前锥角、后锥角、等效直径比及槽道长度4因素3水平共计9组模型的流量传感器特性，得出如下结论：

(1) 前锥角对双锥流量传感器的性能起着特别重要的作用，是影响流出系数最为显著的因素，同时对流出系数线性度以及相对压力损失也有着重要影响；后锥角是影响相对压力损失最显著的因素，对流出系数以及流出系数线性度有一定的影响．

(2) 等效直径比对流出系数以及流出系数线性度有一定的影响，对压力损失的影响较小．

(3) 槽道长度对流出系数线性度以及相对压力损失有一定的影响，对压力损失的影响较小．根据仿真结论，预测DN100双锥流量传感器最优几何参数匹配为前锥角45°，后锥角30°，等效直径比0.65，槽道长度15,mm，并最终通过实流实验验证．

［1］ International Standard Organization. ISO 5167—1：2003 Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full(Part 1)：General Principles and Requirements[S].2003.

［2］ 纪建英，张务铎，翟恒涛. V锥流量计在城市燃气测量中的应用[J]. 城市燃气，2009，11(417)：11-12.

Ji Jianying，Zhang Wuduo，Zhai Hengtao. The using of V-cone flow meter in urban gas measurement[J]. Urban Gasm，2009，11(417)：11-12(in Chinese).

［3］ 徐 英，吴经纬，杨会峰，等. 内锥流量计流出系数预测方法研究[J]. 计算力学学报，2009，26(5)：727-733.

Xu Ying，Wu Jingwei，Yang Huifeng，et al. Predicting discharge coefficient of V-cone flowmeter with four turbulence models[J]. Chinese Journal of Computational Mechanics，2009，26(5)：727-733(in Chinese).

［4］ Peters R J W，Steven R，Caldwell S. Testing the wafer V-cone flowmeters in accordance with API 5.7“Testing Protocol for Differential Pressure Flow Measurement Devices”in the CEESI Colorado test facility[J]. Flow Measurement and Instrumentation，2006，17(4)：247-254.

［5］ Tsunoda Kazumii，Saito Yoshinori. Supersonic flow behavior under strong Lorentz force Effects of area ratio and pressure loss[J]. JSME International Journal Series B：Fluids and Thermal Engineering，1994，37(4)：752-759.

［6］ 徐 英，段玉晗，赵 轶. 文丘里高压湿气测量虚高特性数值模拟[J]. 天津大学学报，2012，45(3)：221-227.

Xu Ying，Duan Yuhan，Zhao Yi，Numerical simulation on high pressure wet gas flowmetering overreading characteristics of verturi tube[J]. Journal of Tianjin University，2012，45(3)：221-227(in Chinese).

［7］ Gan G，Riffat S B. K-factors for HVAC ducts-numerical and experimental determination[J]. Building Services Engineering Research and Technology，1995，16(3)：133-139.

Numerical Simulation and Optimum Design of Double-Cone Flowsensor

Xu Ying1,2，An Junda1,2，Long Zhenghai3，Gao Lu1,2
(1. School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2. Tianjin Key Laboratory for Process Measurement and Control，Tianjin 300072，China；3. Chuan Zhong Division of PetroChina，Southwest Oil and Gasfield Company，Chengdu 610051，China)

Using computational fluid dynamics(CFD)method and orthogonal experiment，the influence of key geometric factors of a new type of double-cone flowsensor，such as fore-and-aft cone angle，equivalent diameter ratio and channel flow length，on the discharge coefficient，linearity and relative pressure loss was investigated，and finally the best optimal match of these geometric factors was predicted. The simulation results show that the fore cone angle of double-cone flowsensor has significant influence on relative pressure loss，the discharge coefficient and its linearity．The aft cone angle has strong influence on the relative pressure loss. The results simulated by CFD are in good agreement with those obtained by actual flow experiment.

double-cone flowsensor；orthogonal experiment method；discharge coefficient；linearity；relative pressure loss

TP212.1

A

0493-2137(2013)11-0984-07

DOI 10.11784/tdxb20131106

2012-05-15；

2012-09-17.

国家自然科学基金资助项目(60974118)；天津市应用基础及前沿技术研究计划资助项目(08JCYBJC1180).

徐 英（1970— ），女，博士，副教授.

徐 英，xuying@tju.edu.cn.