飞机T型尾翼跨音速颤振特性研究

杨 飞，杨智春

(1.中国商飞上海飞机设计研究院 强度部，上海 200232;2.西北工业大学航空学院，西安 710072)

飞机跨音速颤振特性从根本上决定了飞机的颤振包线，事关飞机稳定性安全。通常可以通过试验或计算手段得到飞机的颤振临界耦合模态、临界颤振动压、跨音速颤振动压压缩性系数和颤振裕度。在亚音速(低马赫数)情况下，空气压缩性对颤振速度影响较小，当马赫数大于0.5时，必须考虑空气压缩性的影响，在马赫数等于1.0附近的跨音速区，颤振速度(颤振动压)会急剧降低，形成一个所谓“跨音速凹坑”。

飞机T型尾翼是指平尾位于垂尾稍部，平尾和垂尾组成一个“T字”结构形式的尾翼。T型尾翼结构具有诸多优点，一方面，T型尾翼布局可使平尾避开机翼尾流或尾吊发动机喷流的影响，增大平尾力臂、提高操纵效率;另一方面，T型尾翼构型可以实现后机身大开口，便于大型装备的货物装运，同时T型尾翼的高置平尾可满足水上飞机设计要求。因此，许多大型军用运输机、水上飞机和尾吊发动机布局飞机都选用T型尾翼布局。

从飞机型号设计角度考虑，需要全面准确掌握T型尾翼的跨音速颤振特性和跨音速压缩性修正特性。文献［1］研究了马赫数、平尾上反角和垂尾扭转刚度对T尾颤振特性的影响，文献［2］和文献［3］研究进行了某型T型尾翼的跨音速风洞试验，总结了T型尾翼的跨音速颤振特性。本文从某型飞机T型尾翼跨音速颤振的工程分析方法出发，讨论了飞机T型尾翼跨音速颤振的研究方法，通过计算分析研究马赫数、风洞气流密度、平尾静升力(迎角)对T型尾翼结构跨音速颤振特性的影响规律;通过升力系数斜率空气压缩性修正计算方法和跨音速颤振模型风洞试验数据得到了飞机T型尾翼的跨音速颤振的凹坑曲线和压缩性特性。

1 飞机T型尾翼跨音速颤振研究方法

T型尾翼的结构特点，使得其颤振特性与常规布局尾翼有很大不同，除了在颤振分析计算时需要考虑后机身柔度的影响外，T型尾翼的颤振特性还具有两方面的特点。从气动力方面讲，常规布局尾翼颤振计算中不需要考虑的平尾定常气动力(静升力、迎角)，在T型尾翼颤振中却不可忽略，因为当垂尾发生弯曲振动而带动其稍部的平尾滚转运动时，作用在平尾上的定常气动力在水平和垂直方向上的分量也成为时变的气动力，从而使平尾静升力产生所谓的非定常气动力效应(因而平尾的迎角也成为颤振计算中必须考虑的参数)，显然，进行T型尾翼颤振计算时，如果仍然按常规非交互升力面的处理方法计算T型尾翼的非定常气动力，则还应该采用某种方法对T型尾翼的非定常气动力进行修正以计及这种非定常气动力效应的影响。

现有研究结果表明，T型尾翼的颤振速度一般要比常规布局(低尾)尾翼的颤振速度低，如果不考虑T型尾翼结构的特殊性，按照常规布局尾翼颤振计算方法进行分析，会得到偏高的T型尾翼颤振速度［4－13］。同时，与亚音速颤振特性不同的是，现代T型尾翼构型飞机的均在大马赫数飞行，必须考虑马赫数空气压缩性性对颤振特性的影响。而对于T型尾翼跨音速颤振计算，由于跨音速非定常气动力亚音速计算准确性较高，但是跨音速颤振计算的准确性难以保证。目前的跨音速颤振计算主要集中于机翼、平尾等单翼面的跨音速颤振计算，而对于T型尾翼这种复杂构型在公开资料中较多见到亚音速范围的计算研究，T型尾翼跨音速颤振研究较少，且主要是试验研究［1－3］。虽然 T型尾翼跨音速颤振计算具有一定的难度，但是可以根据目前掌握的 MSC.NASTRAN偶极子格网法(DLM)和ZAERO软件偶极子格网法(ZONA6)计算T型尾翼亚音速颤振特性，用考虑空气压缩性的ZAERO软件等价片条势流跨音速颤振计算方法(ZTAIC)计算T型尾翼跨音速颤振特性。其中，ZTAIC［14］(Transonic Unsteady Aerodynamics using a Transonic Equivalent Strip Method)为跨声速等价片条理论计算跨声速非定常气动力，可输入高速测压试验测得的跨声速定常压力分布数据，求解非定常跨音速小扰动方程得到非定常压力系数，用非定常压力系数修正偶极子格网法计算的线性非定常气动力，非定常压力系数的计算如式(1)所示。式中:C—P为偶格法计算的压力系数，ΔCP为修正压力系数。由于翼型厚度在跨声速区域对颤振有一定影响，ZTAIC方法同时考虑了平尾和垂尾的翼型厚度。通过趋势研究掌握马赫数、平尾静升力(迎角)、风洞密度对T型尾翼跨音速颤振特性的影响。由于T型尾翼跨音速颤振计算的准确性较低，需要采用高速风洞颤振试验方法来得到T型尾翼结构的跨音速颤振特性、跨音速颤振凹坑曲线特性和跨音速颤振空气压缩性。同时，由于高速风洞试验中风洞的不同特点决定了不同的吹风模式，闭口回流式跨音速颤振试验采用固定密度，增加马赫数的吹风方法;开口暂冲式跨音速风洞颤振试验采用固定马赫数，增加静压动压，变密度的吹风方法。由于密度变化，动压变化，开口暂冲式风洞跨音速颤振试验结果是不同密度对应颤振动压组成的跨音速颤振凹坑曲线，因此需要进行风洞密度修正，得到同一基准密度下给定马赫数的颤振动压，组成跨音速颤振凹坑曲线。

所以，如果要准确、全面获得飞机T型尾翼跨音速颤振特性，就需要采用试验为主、计算为辅、计算预估、试验验证的思路，采用趋势与关键点相对比的方法来进行T型尾翼跨音速颤振研究。

2 飞机T型尾翼颤振特性

图1 飞机T型尾翼典型颤振耦合模态Fig.1 Aircraft T－tail classical flutter mode

从颤振机理上讲，T型尾翼存在如图1所示的三种典型颤振类型，分别是垂尾一阶弯曲模态与垂尾一阶扭转模态颤振耦合的垂尾弯扭耦合型;平尾反对称一阶弯曲模态、平尾反对称二阶弯曲模态与平尾反对称一阶扭转模态颤振耦合的平尾反对称弯扭耦合型;平尾对称一阶弯曲模态、平尾对称二阶弯曲模态与平尾对称一阶扭转模态颤振耦合的平尾对称弯扭耦合型，且不同飞机T型尾翼结构具有不同的颤振临界模态。

3 影响飞机T型尾翼跨音速颤振特性的关键参数

通常飞机T型尾翼颤振特性与垂尾扭转刚度、平尾上反角、平尾迎角(静升力)和马赫数密切相关。但是对给定结构形式的T型尾翼结构的颤振特性与马赫数、风洞气流密度和平尾迎角(静升力)相关，这三个参数对飞机T型尾翼跨音速颤振的影响分析如下。

3.1 马赫数对飞机T型尾翼跨音速颤振的影响

马赫数对飞机T型尾翼跨音速颤振动压、颤振频率和颤振模态具有显著影响，且对垂尾弯扭耦合颤振型、平尾反对称弯扭耦合颤振型和平尾对称弯扭耦合颤振型的颤振三种颤振耦合模态类型的颤振动压、颤振频率影响各不相同。对T尾模型用跨音速颤振ZTAIC方法计算的无量纲颤振动压系数与马赫数的变化关系如图2所示，其中无量纲动压系数为各个计算点的颤振动压与最低马赫数的平尾对称弯扭耦合模态性颤振动压的比值。平尾对称弯扭耦合颤振型的颤振动压最小，为临界颤振模态。随着马赫数的增大，颤振动压在亚音速区基本不变，在跨音速区大幅减小，出现明显的下陷，表现出“跨音速颤振凹坑”特征。

图2 ZTAIC法计算T尾模型的颤振动压与马赫数的变化关系Fig.2 The T－tail model flutter dynamic pressure and mach number by ZTAIC method

图3 T尾模型临界颤振动压与大气密度和马赫数的变化关系Fig.3 The T－tail model flutter dynamic pressure with air density and mach number by ZTAIC method

3.2 风洞气流密度对飞机T型尾翼跨音速颤振的影响

在跨音速颤振模型风洞试验中，风洞气流密度并非海平面空气密度，且不同马赫数，风洞气流密度随着动压的变化而变化。因此，为了得到给定马赫数，同一密度下的颤振动压就必须进行密度修正。首先，研究在整个跨音速范围内密度和马赫数对T型尾翼跨音速颤振特性的综合影响;其次，进行风洞气流密度修正。密度修正的根据是假设计算试验风洞气流密度颤振动压与计算海平面密度颤振动压的比值，等于试验风洞气流密度颤振动压(试验动压)与试验海平面密度颤振动压的比值。针对颤振风洞试验的马赫数和密度，计算不同马赫数不同密度的颤振特性，通过式(2)所示关系对风洞试验结果进行修正。

针对某型飞机T尾模型跨音速模型风洞试验，综合考虑不同马赫数和不同空气密度下T尾的跨音速颤振特性，考虑风洞气流密度从1.225kg/m3到4.254kg/m3，平尾迎角0°。同一马赫数T尾高速风洞模型临界颤振动压随空气密的变化关系如图3(a)所示，同一马赫数，平尾对称弯扭耦合颤振动压随空气密度的增大而增大;同一密度，临界颤振动压随马赫数的变化关系如图3(b)所示，临界颤振动压随着马赫数的增大而减小，6个典型空气密度的临界颤振动压曲线显示，在马赫数跨音速区域内，平尾对称弯扭耦合型颤振的颤振动压随着马赫数的增大而急剧减小，表现出跨音速颤振凹坑曲线中的“下陷”趋势。

3.3 平尾迎角对飞机T型尾翼跨音速颤振的影响

三种不同T尾模型在迎角0°、3°和－3°，定义迎角抬头为正，马赫数0.82时的临界颤振动压变化趋势如图4所示。无量纲颤振动压系数为相对0°迎角T尾模型的动压比值。对平尾弯扭耦合颤振型，平尾正迎角使颤振动压减小，负迎角使颤振动压增大。且在小迎角范围(±3°)内，颤振速度变化较小，这与理论分析［9］结论相一致。说明颤振风洞试验时的平尾零升状态时的小量迎角误差对颤振边界影响较小。

图4 T尾模型临界颤振动压与迎角的变化关系Fig.4 The T－tail model flutter dynamic pressure with attack angle by ZTAIC method

4 飞机T型尾翼跨音速颤振的空气压缩性修正

飞机设计中，最简单的方法是预估“跨音速凹坑”最低点颤振动压。飞机飞行中结构上的升力，即气动力载荷直接来源于动压和升力系数，动压与速度(马赫数)、大气密度(高度)相关;而升力系数与压力系数、翼型相关，因此可以用升力系数来分析跨音速颤振动压和颤振速度的空气压缩性修正。

文献［15］将颤振裕度预测方程表示为:

对一架飞机，发生颤振时颤振裕度F等于0，对应的颤振边界CLαq是一定值。因此对不同的空气压缩性情况，在不同马赫数其升力线斜率CLα和速压q是相对应的。如式(4)所示。

密度 ρ相同，则式(4)简化为:

定义颤振速度空气压缩性修正系数为CV，不同压缩性速度修正关系如式(6)所示:

则速度压缩性系数为:

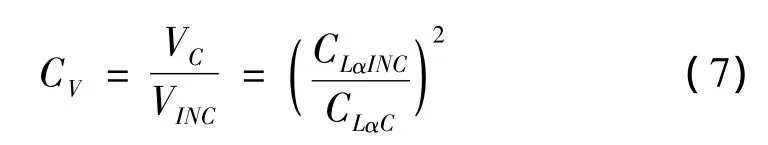
动压压缩性系数为:

每个马赫数下都有一个压缩性修正系数，根据跨音速压缩性修正系数随马赫数变化的曲线得到跨音速凹坑曲线关系。其中，对不可压升力系数CLαINC，一方面可以通过马赫数试验获得，另一方面也可以通过专业气动力计算软件获得。在亚音速范围内，计算升力系数与测压试验的升力系数是近似相同的。在跨音速范围内，由于激波难以准确模拟，计算跨音速升力系数不准确;用全机高速测压风洞试验可以测得较准确的飞机跨音速升力系数。因此，可以用风洞试验的亚音速和跨音速升力系数结果进行跨音速颤振的空气压缩性修正系数计算。

图5 不同方法得到的飞机T型尾翼模型颤振动压与马赫数的变化关系Fig.5 The T－tail model flutter dynamic pressure with mach number by different method

升力系数斜率系数空气压缩性修正方法存在一定的局限性。一方面，如果输入数据不足就不能得到整条跨音速颤振凹坑曲线，因而不能得到临界马赫数和跨音速颤振空气压缩性修正系数;另一方面，针对单翼面(机翼、平尾)弯扭耦合的压缩性系数不一定适用于T型尾翼、V型尾翼、H型尾翼等特殊翼面。所以，必须通过高速颤振模型风洞试验确定如图5所示的各个马赫数下的颤振动压，通过整体分析得到跨音速颤振空气压缩性修正系数。图5给出了T尾模型在马赫数0.7至0.95跨音速范围的风洞试验结果和升力系数斜率计算结果，其中对风洞试验结果进行了风洞气流密度修正。图5中无量纲颤振动压系数为各个点的颤振动压与凹坑最低点颤振动压的比值。图5表明，一方面，马赫数对T型尾翼跨音速颤振动压有显著影响，T尾跨音速颤振动压随着马赫数的增大而减小，且在接近凹坑最低点颤振动压大幅减小，过凹坑后颤振动压逐渐增大。另一方面，密度修正对跨音速压缩性修正系数有一定的影响，密度修正前采用风洞试验空气密度得到的T尾颤振压缩性系数略大于密度修正后海平面空气密度得到的T尾颤振压缩性系数。此外，基于全机高速测压模型风洞试验结果，采用升力系数斜率修正方法进行跨音速颤振压缩性，升力系数斜率计算的无量纲颤振动压系数与风洞试验得到的结果，在马赫数0.7和0.89吻合较好。说明基于试验数据的“升力线系数斜率跨音速颤振速度压缩性修正”方法可用于跨音速颤振空气压缩性修正计算。

5 结论

(1)飞机T型尾翼跨音速颤振研究方法比较复杂。因为飞机T型尾翼具有平尾、垂尾在结构和气动方面相互耦合的特点，T尾跨音速非定常气动力难以准确计算，所以T型尾翼跨音速颤振计算较难实现，精确度较低。如果要准确、全面获得飞机T型尾翼跨音速颤振特性，就需要采用试验为主、计算为辅，计算预估、试验验证的思路，采用趋势与关键点相对比的方法来进行T型尾翼跨音速颤振研究。

(2)马赫数对T型尾翼跨音速颤振动压有显著影响。T尾跨音速颤振动压随着马赫数的增大而减小，且在接近凹坑最低点颤振动压大幅减小，过凹坑后颤振动压逐渐增大。

(3)某型飞机T尾跨音速颤振试验数据分析结果表明，风洞气流密度修正对跨音速压空气缩性系数有一定的影响，密度修正前采用风洞试验的空气密度得到的T尾颤振速度压缩性修正系数略大于密度修正后海平面空气密度得到的T尾颤振压缩性修正系数。

(4)基于试验数据的“升力系数斜率跨音速颤振空气压缩性修正”方法可用于跨音速颤振分析。

［1］Land N S，Fox A G.An experimental investigation of the effects of mach number，stabilizer dihedral，and fin torsional stiffness on the transonic flutter characteristics of a tee－tail［R］.NASA TN D －924.1961.

［2］张天肖.T型尾翼跨音速颤振模型风洞试验研究［R］.中国航空工业总公司上海飞机设计研究所－技术报告，1995，11:11 －17.

［3］吴兴世.T尾跨音速颤振研究［R］.中国航空工业总公司上海飞机设计研究所－技术报告，1995，11:7－13.

［4］Jennings W P，Berry M A.The flutter analysis of T－Tail［J］.AIAA Journal，1975，759:1 －4.

［5］Jennings W P，Berry M A.Effect of stabilizer dihedral and static lift on T－Tails flutter［J］.Journal of Aircraft，1977，14(4):364－367.

［6］Emil Suciu. MSC/NASTRAN flutter analyses of T－Tails including horizontal stabilizer static lift effects and T－Tail transonic dip［J］.The 1996 Msc/Nastran World User’S Conference.Newport Beach.CA，June，1996:1－10.

［7］Quarantal G， Riccil S， Scottil A， et al. Aeroelastic investigation and design improvements on a three surface transport airplane［J］.XVIII Congresso Nazionale AIDAA，Settembre 2005，VOLTERRA(PI):19－22.

［8］Chuban V D.Influence of angle of attack and stabilizer deflection on T empennage flutter［J］.Journal of Aircraft.2005，42(1):264－268.

［9］刘如铭.偶格法进行低速T尾颤振分析［R］.中国航空工业总公司上海飞机设计研究所－技术报告，1993，4:7－13.

［10］刘成玉，王利京.平尾上反角和静升力对T尾颤振的影响［J］.飞机工程，2005，3:9 －12.LIU Cheng－yu，WANG Li－jing.Effect of stabilizer dihedral and static lift on T－Tails flutter［J］.Aircraft Engineering，2005，3:9 －12.

［11］吕 斌，吴志刚，杨 超.T型尾翼颤振特性分析方法［J］.工程力学，2008，2，25(2):230 －234.LÜ Bin，WU Zhi－gang，YANG Chao.Analysis of T－tail flutter［J］.Engineering Mechanics，2008，2，25(2):230 －234.

［12］杨 飞.飞机 T型尾翼结构模态局部化及颤振特性研究［D］.西安:西北工业大学，2009.

［13］杨 飞，杨智春.模态局部化对T型尾翼颤振特性的影响［J］.振动与冲击，2010，29(1):1 －4.YANG Fei，YANG Zhi－chun.The effects of mode localization on T－tail flutter characteristic［J］.Journal of Vibration and Shock，2010，29(1):1 －4.

［14］ZAERO theoretical manual［M］.USA.ZONA Technology，Inc，2008:1 －4.

［15］Zimmerman N H，Weissenburger J T.Prediction of flutter Onset speed based on flight testing at subcritical speeds［J］.Journal of Aircraft，1964，4(1):190－202.