上海环球金融中心结构模态测试

韦 晓，郭 迅

(1.上海市地震局，上海 200062;2.中国地震局 工程力学研究所，哈尔滨 150080)

模态是结构的固有特性，结构模态包括结构以小振幅振动时的固有频率、各固有频率对应的振型以及反映结构耗能特性的阻尼比。在结构设计分析阶段，模态是研究结构地震及风动力响应规律的重要参数。对于超高层建筑，各阶模态频率分布规律(频率比)及振型形状往往可以反映结构的整体变形模式。比如匀质剪切杆各阶频率之比为1∶3∶5…，而匀质弯曲杆各阶频率之比为1∶6.4∶17.5…。已建成结构的实测模态还可以用来标定结构设计分析阶段的数值模型结果或缩尺物理实验模型结果，反复获得这样的反馈，对于设计和研究人员建立自信、提高设计水准很有帮助。2011年3月11日日本东部M9.0地震中，位于震中西南370 km外的东京某29层钢框架结构(Kogakuin大学)获得了地面运动及结构各代表楼层的地震响应记录。该结构短轴向实测平动固有频率分别0.323 Hz、1.058 Hz和2.139 Hz，频率比大致与剪切型变形模式相吻合。第一振型频率在结构顶部几层的位移响应中占绝对优势，但是，在强迫振动阶段(地震动主要峰值尚未经历完毕)，顶部几层的加速度响应中，第二振型贡献最大，其次是第一振型，然后是第三振型。这一实例十分清楚地表明，结构模态对于设计和研究人员判断结构地震响应极其重要。

上海环球金融中心位于上海浦东陆家嘴金融贸易区，是目前我国大陆地区投入使用的最高建筑，主楼地下3层，地上101层，地面以上高度492 m，建筑平面57.95 m ×57.95 m，主体建筑面积252935 m2。结构体系为钢与混凝土混合结构;主体结构为巨型柱、巨型斜撑、带状桁架以及核心筒构成的三维巨型框架－筒结构，钢筋混凝土核心筒通过外伸钢桁架与巨型柱相连。结构外轮廓及主要结构构件的相互关系如图1所示;结构41层以下呈正方形布置，往上则在东西向对称收缩，平面呈梭形，下部及上部代表性平面示于图2中。本文定义南北向为长轴(X向)、东西向为短轴(Y向)，用脉动法分别测试了该结构双水平向和扭转振动频率、振型和阻尼比。

图1 环球金融中心外轮廓及结构构造Fig.1 Outline and structural configuration of the World Financial Center

1 测试仪器选择

测试仪器主要包括振动传感器和数据采集仪。参考既有研究结果并结合经验判断，环球金融中心平动第一振型周期大致在10 s左右，对应的脉动加速度信号十分微弱。为了克服长周期、信号微弱这两个难点，经过排查选择具有高增益的力平衡加速度传感器。该传感器具有噪音低、灵敏度高、线性相位以及通频带从零频起始等优点。由于噪声低和灵敏度高，才能测试非常微弱的振动信号;线性相位可以保证所测试的多个模态频率叠加的信号不致产生畸变;从零频起始才能保证近10 s周期的低频信号能够被测试到。这四个主要技术指标的组合是其他类型传感器难以满足的，传感器的具体指标列于表1第一和第二列。

表1 环球金融中心模态测试选用仪器技术指标Tab.1 The technical index of model testing instrument for the SWFC

对于测试十分微弱的信号，必须小心选择数据采集仪。测试时，试用了三种美国生产的采集仪，其中两种分辨率为24 Bit、固定量程(±10 V)的采集仪均无法识别脉动信号，只有表1中所列的采集仪能够很好地识别脉动信号。美国Spectral Dynamics公司生产的Siglab采集仪尽管分辨率只有16 Bit，但由于其量程可以调低至±20 mV，这与±10 V量程相比又增加了约9 Bit;此外Siglab采集仪还具有－96 dB的抗混叠(Anti-aliasing)滤波功能;并且传感器、采集仪以及采集电脑全采用直流供电，系统干扰被降低到最小，因此得到了十分理想的脉动信号。

2 短轴方向(Y向)测试

2009年3月12日中午开始采集信号，当时小雨，偏南风3～4级。由于能够分辨微弱脉动信号的采集仪只有4个通道，传感器的布置要照顾到两个方面:一般结构顶部楼层振动信号比较明显，该处要布设传感器;沿竖向布设时间隔要尽量均匀，以保证测得尽量多的振型。结合现场布线条件，在环球金融中心上半部沿短轴方向(Y向)在101层(通道1)、96层(通道2)、90层(通道3)和66层(通道4)靠近楼层平面形心位置(图2)布置了力平衡加速度传感器。设置采集参数时，用20段脉动信号进行算数平均，每段持时25 s，采样频率12.8 Hz，低通滤波频率上限 5.0 Hz，频率分辨率为 0.04 Hz。

图2 结构下部(30层)及上部(90层)平面图Fig.2 Plan view of lower level(30 F)and up level(90F)

各通道测得的时域信号及对应的自功率谱示于图3中。时域图显示，各通道信号均受第一振型频率控制，顶层(101层)叠加的高阶振型频率比其他通道更明显。各层加速度幅值都很小，顶层只有1.2 cm/s2，仅相当于重型卡车从普通多层砌体房屋窗前快速驶过时引起各层楼板的水平振动幅值。频域图中纵坐标采用对数刻度，这样可以显示出幅值很低的高阶频率，各频率峰值列于表2中，表中第一行用序号标示各阶频率，各自对应的振型还须通过信号相位分析确定。具体操作时，对时域信号进行傅里叶变换，比对各个通道傅里叶系数虚部(或实部)在各个峰值频率处取值的正负，如果同号，则为同相，异号为反相。据此可方便地识别出平动第一、第二、第三振型频率分别为0.16 Hz、0.52 Hz和0.92 Hz;其他峰值频率可能是平动更高阶振型频率或扭转振动频率，有待用排除法进一步确认。

表2 短轴方向(Y向)脉动信号对应的各阶固有频率和振型Tab.2 Various natural frequencies and its model shapes corresponding to ambient vibration in transverse direction(Y axis)

3 长轴方向(X向)测试

与短轴方向测试类似，将传感器顺时针转动90°，重新固定，以相同参数设置进行测试，得到的101层(通道1)、96层(通道2)、90层(通道3)和66层(通道4)X方向脉动信号示于图4。时域图中各通道信号仍然受第一振型频率控制，顶层(101层)叠加的高阶振型频率比其他通道明显。这一时段，顶层加速度幅值更小，仅有0.4 cm/s2，为短轴方向的三分之一。自功率谱图中各频率峰值列于表3中，结合相位分析，识别出了平动第一、第二、第三振型频率分别为0.16 Hz、0.52 Hz和 0.92 Hz。

表3 长轴方向(X向)脉动信号对应的各阶固有频率和振型Tab.3 Various natural frequencies and its model shapes corresponding to ambient vibration in longitudinal direction(X axis)

4 扭转方向测试

扭转振动系指各楼层平面绕经过形心的竖直轴的转动。显而易见，楼层越高扭转振动应该更明显，并且从平面上看，距形心越远，振动也越明显，因此在结构上半部选长轴两端101层F2点(通道1)、101层F1点(通道2)、78层F1点(通道3)和78层F2点(通道4)，采集Y方向信号，其中各楼层的F1点或F2点在水平面上的投影重合。图5(a)图5(b)分别为101层和78层长轴两端的沿短轴(Y向)脉动时域信号和对应的自功率谱。显然，平动第一振型频率仍然占主导，但在该振型叠加的高频信号仍可清晰地分辨出上下反相的信号，依测点位置和相位判定:0.16 Hz为Y向平动第一阶频率;0.48 Hz为扭转第一阶频率;1.50 Hz为扭转第二阶频率。

图3 短轴向代表楼层水平向脉动时程及其自功率谱图Fig.3 Time history and corresponding auto-spectrum of horizontal ambient vibration at typical floors in transverse direction

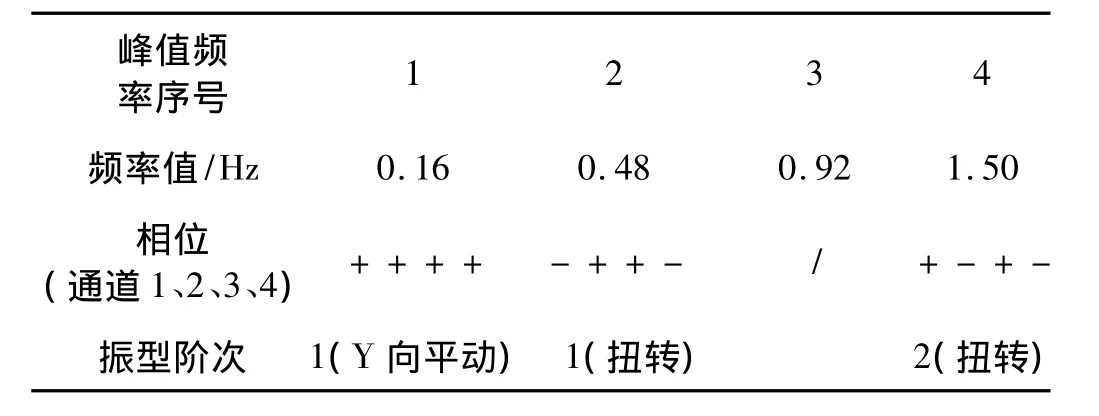
表4 扭转脉动信号对应的各阶固有频率和振型Tab.4 Various natural frequencies and its model shapes corresponding to torsion natural frequency and its model shapes

5 振型识别结果

经过上述频率识别过程后，可以确认短轴、长轴向前三阶及扭转方向的前两阶固有频率，将每一频率对应的傅里叶变换复幅值进行归一化处理，就得到对应频率的振型。图6和图7分别为短轴向(Y向)第一振型(f=0.16 Hz)和第二振型(f=0.52 Hz);长轴向(X向)第一和第二振型与短轴向类似，不再画出。扭转第一振型指被测的两个楼层(101层、78层)以0.48 Hz按同相位绕竖直形心轴往复转动;扭转第二振型指被测的两个楼层(101层、78层)以1.50 Hz按反相位绕竖直形心轴往复转动。

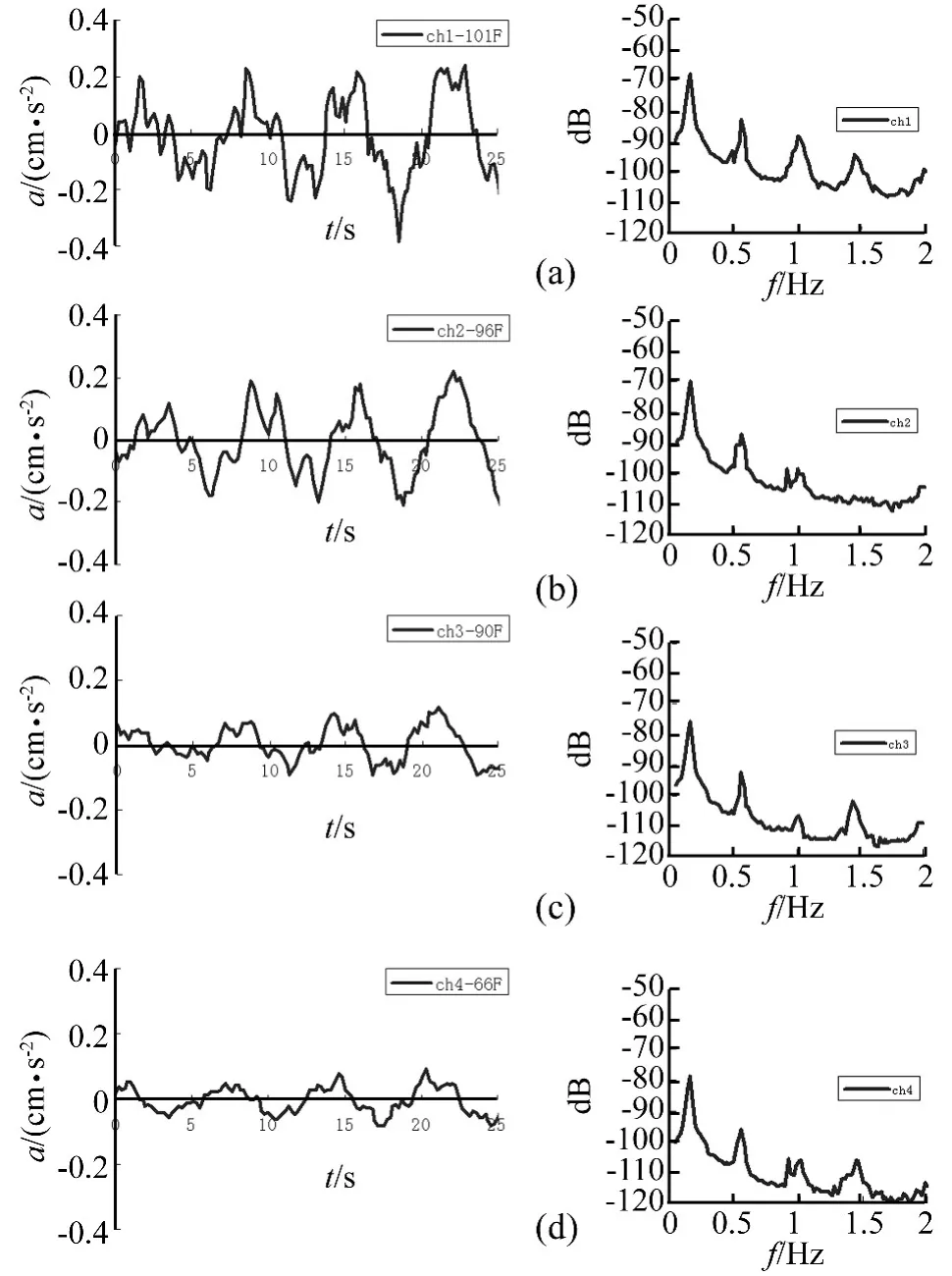
图4 长轴向代表楼层水平向脉动时程及其自功率谱图Fig.4 Time history and corresponding auto-spectrum of horizontal ambient vibration at typical floors in longitudinal direction

图5 代表楼层水平向扭转脉动时程Fig.5 Time history of horizontal torsion ambient vibration at typical floors

6 阻尼识别结果

在图1所示的自功率谱图上，对应每一个频率峰值应用半功率点法计算短轴向(Y方向)阻尼比;同样，用图2所示的自功率谱图可计算长轴向(X方向)阻尼比，结果列于表5。扭转向自功率谱图不规则，难以计算阻尼比。表5的结果表明，双水平向阻尼比都比常规高层建筑阻尼比大一倍左右，这可能与该建筑在90层设置的调谐阻尼器(TMD)有关;二、三阶阻尼比在正常范围。

图6 短轴向(Y向)平动第一振型(f=0.16 Hz)Fig.6 The first Horizontal model shape in transverse direction(Y axis)(f=0.16Hz)

图7 短轴向(Y向)平动第二振型(f=0.52 Hz)Fig.7 The 2nd Horizontal model shape in transverse direction(Y axis)(f=0.52Hz)

表5 阻尼比测试结果汇总Tab.5 Summary results of the damping ratio test

7 与有限元及模型实验结果的对比

上海环球金融中心在设计阶段除开展了系统的有限元分析，还通过1/50比例缩尺模型实验研究了其模态和地震响应。文献［2］给出了有限元(FEM)和缩尺模型(模型)得到的模态频率，文献［3］则仅给出缩尺模型导出的模态频率，两个文献的结果与本文实测结果的对比列于表6。可以看出，对于平动和扭转一阶振型频率，三者吻合较好;对于平动二阶振型频率，两文献给出的结果都偏高;对于扭转二阶振型频率，文献［2］的结果与实测相符，文献［3］结果偏低较多。

表6 现场实测与有限元及模型实验结果的对比Tab.6 Results comparison among ambient vibration test，FEM model computation and model experiment test

8 结论

上海环球金融中心作为巨型柱、巨型斜撑、带状桁架以及核心筒构成的三维巨型框架－筒形式的钢与混凝土混合结构，系目前我国大陆最高的超高层建筑，结构材料和形式有大胆创新。结构模态系衡量结构分析结果可靠性的重要参数。本文通过合理选择传感器和数据采集器，克服了长周期、信号弱的困难。经分析、整理，得到了结构双向平动和扭转振动频率和振型，这些信息可以作为结构设计人员确认或改进设计阶段结构分析结果的依据。实测模态频率具有以下特点:①双向平动前三阶频率相等，没有体现出上半部平面分长、短轴的影响;② 作为101层、近500 m的结构，其第一自振周期长达6.7 s，该周期值可供以后设计类似材料、高度和结构形式的超高层建筑参考;③ 双向平动第二阶频率以及扭转一阶频率几乎相等(约为0.5 Hz)，这表明，结构在这个频率附近很容易引发共振;④平动一阶、二阶和三阶频率比接近匀质剪切变形模式的比值，按照Housner推导的关于截面渐缩伸臂梁固有频率的公式估算，这一比值也是合理的。

［1］Kasai K，Chuan W，Wada A.Responses of tall buildings in tokyo during the 2011 Great East Japan Earthquake［C］.Presentation at he 4thKwang－Hua Forum and Opening Symposium of Tongji Shaking Table Array ，Shanghai，Dec.11－12，2011.

［2］朱杰江，吕西林，邹 昀.上海环球金融中心模型结构振动台试验与理论分析的对比研究［J］.土木工程学报，2005，38(10):18－26.ZHU Jie－jiang，LÜ Xi－lin，ZOU Yun.Comparison between shaking table tests and analytical results on Shanghai Global Financial Center［J］.Journal of Civil Engineering，2005，38(10):18－26.

［3］邹 昀、吕西林.超高层巨型结构振动特性研究［J］.世界地震工程，2007，23(2):125 －130.ZOU Yun，LÜ Xi－lin.Study on dynamic properties of high rise mega structure［J］.Journal of World Earthquake Engineering，2007，23(2):125 －130.

［4］邹 昀，吕西林，卢文胜，等.上海环球金融中心大厦整体结构振动台试验设计［J］.地震工程与工程振动，2005，25(4):54－59.ZOU Yun，LÜ Xi－lin，LU Wen－sheng，et al，Model design of Shanghai Global Financial Center for shaking table tests［J］.Journal of Earthquake Engineering and Engineering Vibration，2005，25(4):54－59.

［5］郭 迅，阎砺铭，裴 强，等.新型数据采集分析系统及其在工程振动中的应用［J］.地震工程与工程振动，2002，22(4):60－65.GUO Xun，Yan Li－ming，PEI Qiang，et al.New type of data logger system and its application in engineering vibration［J］.Journal of Earthquake Engineering and Engineering Vibration，2002，22(4):60－65.

［6］郭 迅，李洪涛，王金国.某悬索桥振动特性现场测试及数值模拟［J］.世界地震工程，2008，24(3):1 －7.GUO Xun，LI Hong－tao，WANG Jin－guo，Modal parameters measurement and numerical simulation of a cable stayed bridge［J］.Journal of World Earthquake Engineering，2008，24(3):1－7.

［7］Housner G W，Keightley W O.Vibrations of linearly tapered cantilever beams［J］.Engineering Mechanics Division，Proceedings of the American Society of Civil Engineers［J］.April，1962，88(EM2):352 －380.