深水锚泊线串联浮筒系统的动力特性分析
乔东生 , 闫 俊 , 欧进萍 ,
(1.大连理工大学 深海工程研究中心,大连 116024;2.大连理工大学 海岸和近海工程国家重点实验室,大连 116024)
随着海洋石油工业向深水海域的发展,对海洋浮式结构物锚泊系统的定位能力提出了更高、更严格的要求。传统的悬链式锚泊系统多采用钢链和钢索组合而成,随着水深的增加导致其自重增加与水平刚度减少。同时,在深水中呈悬链线形状的锚泊线覆盖了相当大的一部分水域,影响了当地管线和缆索的铺设以及其它船舶在该海域的锚泊定位。串联浮筒锚泊系统能很好地解决这一问题。相对于传统的锚泊系统而言,串联浮筒锚泊系统动力特性更为复杂,研究其动力特性,对判断平台稳定性和安全性尤为重要。
到目前为止,对串联浮筒锚泊系统的研究相对较少,Nakajima等[1]采用有限差分法计算了由多种材料组成的带浮筒系泊系统的动力响应。Mavrakos等[2-4]通过实验与数值分析相结合的方法,系统地研究了浮筒大小、数量和位置等参数的选取对锚泊线力学性能,尤其是动力性能的影响,动力分析分别采用了频域法和时域法,可以考虑浮筒的水平、竖向运动和转动。
王冬姣[5]对由三段具有不同单位长度质量和尺度的索链和浮子/沉子组成的复合锚泊线进行了静力计算,分析中考虑了索链的弹性伸长及与索链直接相连的浮子/沉子的尺度作用。王道能[6]在忽略波浪力的情况下,建立了带有浮筒锚泊系统的动力方程,用数值方法计算了一些特殊点上的受力状态。Kwan等[7]对常用的频域法、时域法和准静定法进行了比较,结果表明:准静定法计算精度较差;频域法计算简单,但其仅可以计算线性问题或弱非线性问题;时域法可以计算所有锚泊系统的动力问题,但其计算量较大且耗时较长。
本文在时域范围内建立锚泊线的动力分析模型,基于能量耗散计算锚泊阻尼,分析串联浮筒系统对锚泊线张力和阻尼的影响特征,进而对串联浮筒的数量和位置进行参数敏感性分析。
1 非线性有限元时域分析
1.1 运动控制方程

在分析锚泊线的运动响应时,一般将锚泊线假定为完全挠性构件,其运动控制方程一般采用Berteaux[8]提出的其中:m,ma分别为单位长度锚泊线质量和附加质量;分别为锚泊线速度矢量和流场速度矢量为锚泊线张力为单位长度锚泊线净重力分别为单位长度锚泊线的法向和切向拖曳力分别为单位长度锚泊线的法向和切向惯性力,可分别表示为:

其中:ρw为海水密度;CDt和CDn分别为切向和法向拖曳系数;D为锚泊线等效直径和分别为流体和锚泊线之间的相对切向和法向速度;CIt和CIn分别为切向和法向惯性力系数和分别为锚泊线的法向和切向速度分量和分别为流体在锚泊线的法向和切向速度分量。
1.2 非线性有限元求解
根据式(1)可知,锚泊线的运动控制方程是一个复杂的时变强非线性方程,需要采用数值方法进行求解,本文采用非线性有限元法进行求解计算。
采用单纯主从接触算法[9],假定海床为刚性海床平面,将锚泊线和海床分别划分为从面和主面,可考虑两者之间滑动摩擦的情况。根据等效截面积相同,将浮筒简化为等径的锚泊线单元,即可采用统一的混合梁单元来模拟锚泊线,然后使用Newton-Raphson迭代法直接求解非线性问题。
2 阻尼计算原理
考虑锚泊线在平面内运动,在一个运动周期τ内锚泊线耗散的能量E可以表示为:

阻尼可以等效为线性化的阻尼系数B,所以,某一时刻的瞬时张力Tn可以近似表示为:

假定锚泊线顶端导缆孔处的运动时程和上部平台的运动时程相同,而平台在波浪作用下的运动响应q(t)假定为正弦运动,即q=q0sin(ωt),其中q0为平台运动响应幅值。所以,一个运动周期τ内锚泊线耗散的能量E可以近似的表达为:

因此,根据计算得到的一个运动周期τ内锚泊线耗散的能量E就可以得到等效线性化的阻尼系数:

其中,耗散的能量E可以通过积分一个周期内的顶端张力-位移曲线得到,需要利用到有限元动力计算的结果。
3 计算模型及参数
锚泊线的材料特性如表1所示[10]。工作水深条件为1500 m,初始平衡位置时的水平投影长度为3342.9 m。初始悬链线找形参考文献[11]采用的静力分析步骤,可以保证在模型中自动包括了锚泊线有关的初始应力和刚度。动力分析时为避免突加荷载对计算结果的影响,对每种工况计算6个周期,取稳态计算结果分析处理。
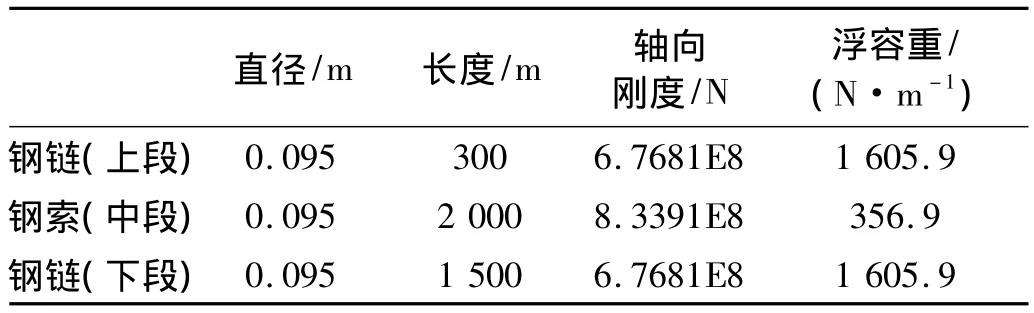
表1 锚泊线材料特性Tab.1 Line physical properties
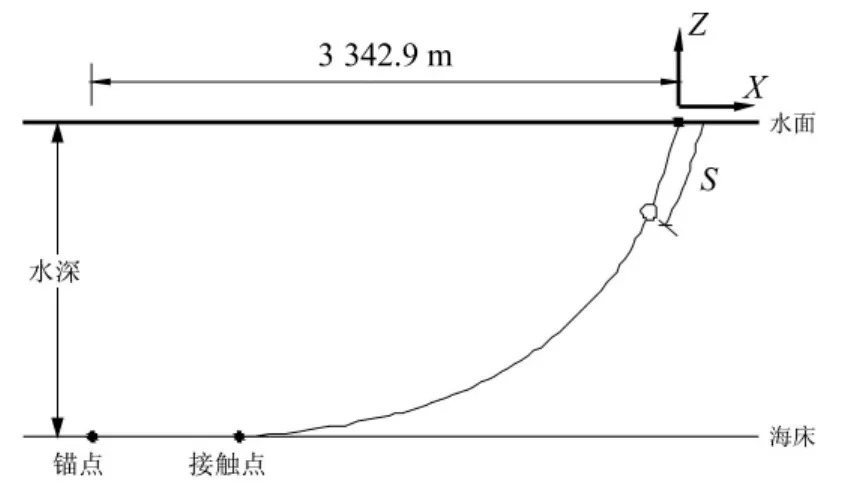
图1 浮筒布置图Fig.1 Buoy layout
考虑4种球形浮筒类型,其直径和浮重如表2所示。浮筒所处位置S分别为300 m,475 m,630 m,950 m,1900 m(如图1所示)。分别考虑锚泊线顶端激励为水平和竖向两个方向,激励周期和幅值根据典型半潜式平台的纵荡和垂荡响应极值来选择确定[10]。乔东生等[12]对深水悬链锚泊线阻尼的研究结果表明:锚泊阻尼随着锚泊线顶端激励幅值的增大而线性增大。因此,本文计算时,仅考虑锚泊线顶端激励周期的变化,计算选取的各种工况如表3所示。
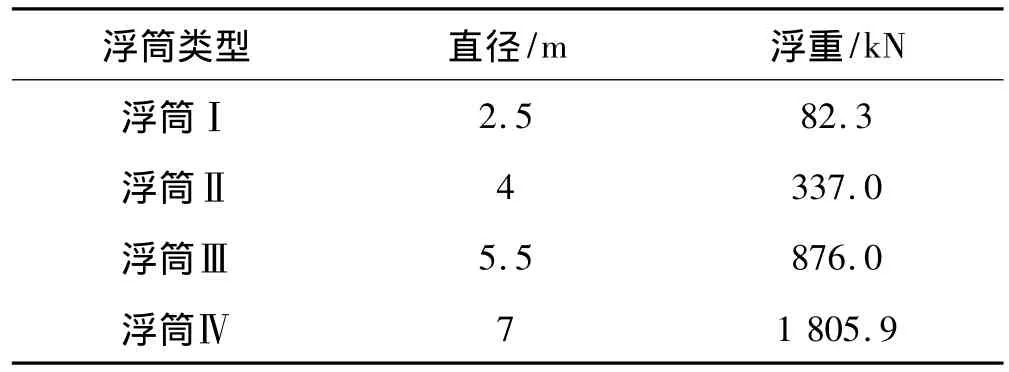
表2 浮筒材料特性Tab.2 Buoy physical properties
4 计算结果及分析
当浮筒所处位置S为950 m,不同浮筒类型变化时的锚泊线初始形态如图2所示;对于浮筒IV,当其所处位置S变化时的锚泊线初始形态如图3所示。锚泊线串联浮筒系统在表3所示不同工况下顶端最大动张力和锚泊阻尼的计算结果如图4~13所示。受篇幅限制,仅列出当S=300 m,630 m,1900 m时,不同浮筒类型变化的结果;仅考虑浮筒II和浮筒III,当其所处位置S变化时的结果。

表3 计算参数Tab.3 Calculation parameters variation
从图4(a)、6(a)、8(a)可见,在锚泊线顶端水平激励下,其顶端动张力随着激励周期的增加而呈递减趋势,串联浮筒系统降低了锚泊线顶端的最大动张力,且随着浮筒浮力的逐渐增加,动张力逐渐降低。同时,随着串联浮筒位置S逐渐向锚固点靠近时,其动张力降低程度逐渐变大。针对串联浮筒Ⅲ和浮筒Ⅳ,其动张力对顶端激励周期的变化逐渐趋于不敏感(如图8(a)所示),原因在于:串联浮筒使得锚泊线形态变为2段(如图2~3所示),且上段总长保持不变,而其顶端动张力主要由上段锚泊线贡献所致。

图2 浮筒大小变化时的锚泊线形态Fig.2 Mooring line configuration under different buoy size
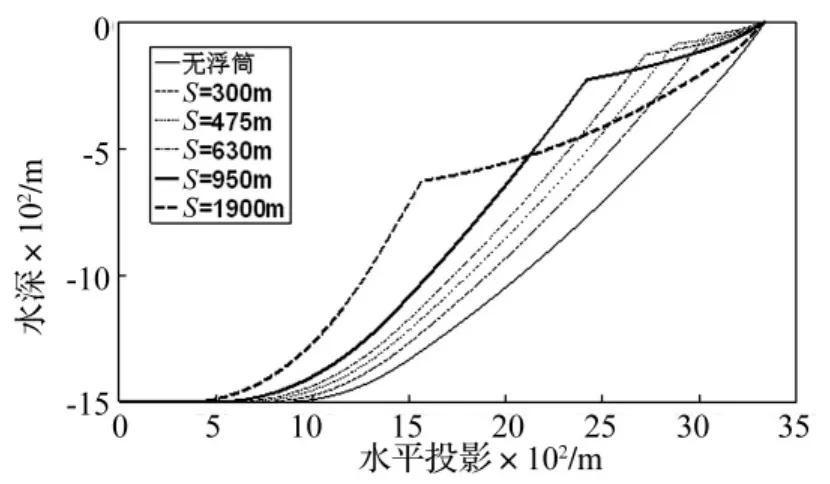
图3 浮筒位置变化时的锚泊线形态Fig.3 Mooring line configuration under different buoy location
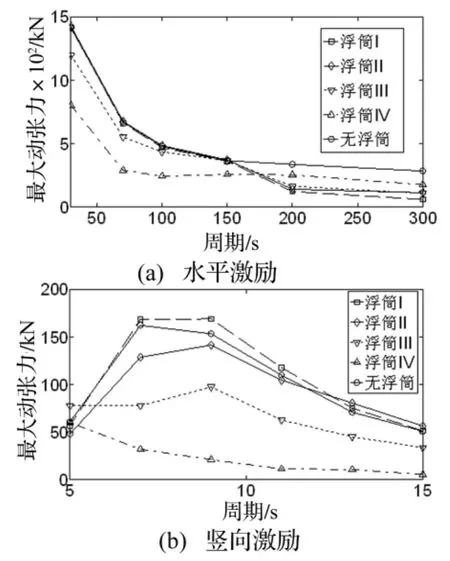
图4 锚泊线顶端最大动张力(S=300 m)Fig.4 Maximum dynamic tension at the top(S=300 m)
从图4(b)、6(b)、8(b)可见,在锚泊线顶端竖向激励下,其顶端动张力随着激励周期的增加总体呈先增加后递减的趋势,串联浮筒系统降低了锚泊线顶端的最大动张力,且随着浮筒浮力的逐渐增加,动张力逐渐降低。随着串联浮筒位置S逐渐向锚固点靠近时,其动张力对顶端激励周期的变化逐渐趋于敏感,且最大动张力对应的卓越激励周期逐渐减小,原因同样由于锚泊线形态发生了变化,其顶端动张力随着上段锚泊线长度的增大而增大。
从图10(a)和图12(a)可见,在锚泊线顶端水平激励下,随着浮筒所处位置S逐渐向锚固点靠近时,其动张力降低程度逐渐变大,且对顶端激励周期的变化同样地逐渐趋于不敏感(如图12(a)所示),原因同样是由于锚泊线形态的变化而导致。
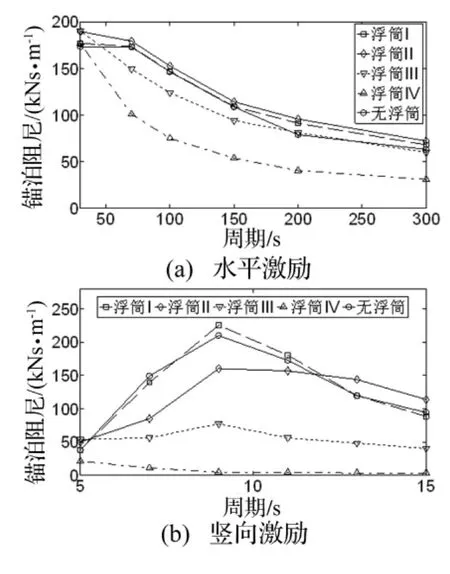
图5 锚泊阻尼(S=300 m)Fig.5 Mooring damping(S=300 m)

图6 锚泊线顶端最大动张力(S=630 m)Fig.6 Maximum dynamic tension at the top(S=630 m)
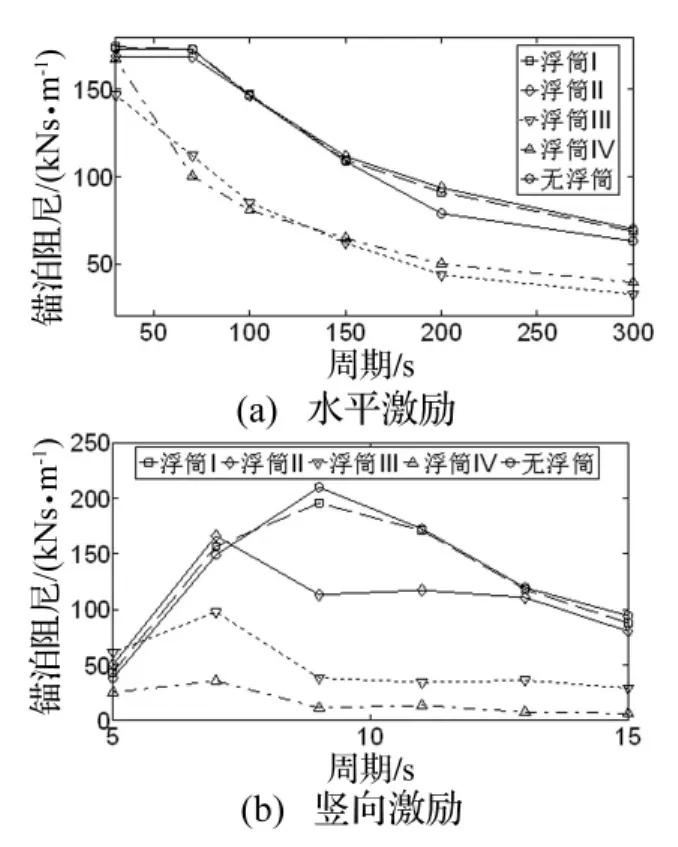
图7 锚泊阻尼(S=630 m)Fig.7 Mooring damping(S=630 m)
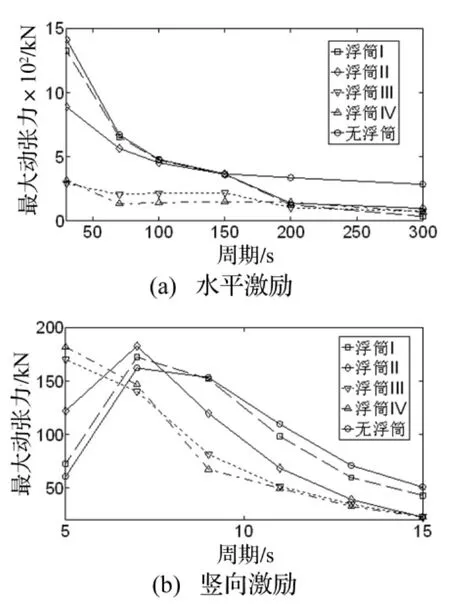
图8 锚泊线顶端最大动张力(S=1900 m)Fig.8 Maximum dynamic tension at the top(S=1900 m)
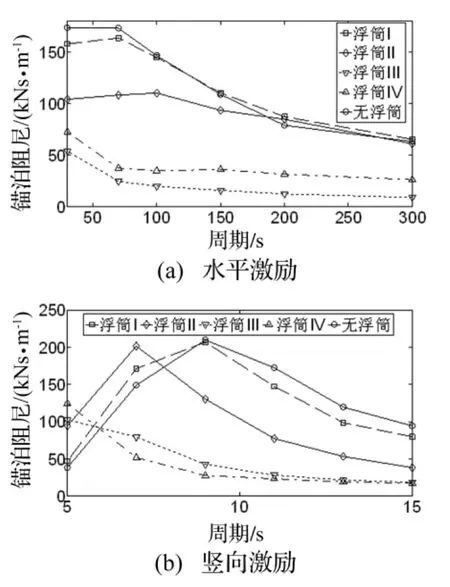
图9 锚泊阻尼(S=1900 m)Fig.9 Mooring damping(S=1900 m)

图10 锚泊线顶端最大动张力(浮筒II)Fig.10 Maximum dynamic tension at the top(Buoy II)
从图10(b)和图12(b)可见,在锚泊线顶端竖向激励下,随着浮筒所处位置S逐渐向锚固点靠近时,其动张力降低程度逐渐变大,且最大动张力对应的卓越激励周期逐渐减小,原因同样是由于锚泊线形态的变化而导致。
从图5、图7、图9、图11和图13可见,锚泊阻尼的变化规律与顶端动张力的变化规律相同,串联浮筒系统降低了锚泊阻尼的贡献。根据上文的锚泊阻尼计算原理,由于串联锚泊系统降低了顶端动张力,因此锚泊线在一个激励周期内耗散的能量减小,进而使得锚泊阻尼变小。
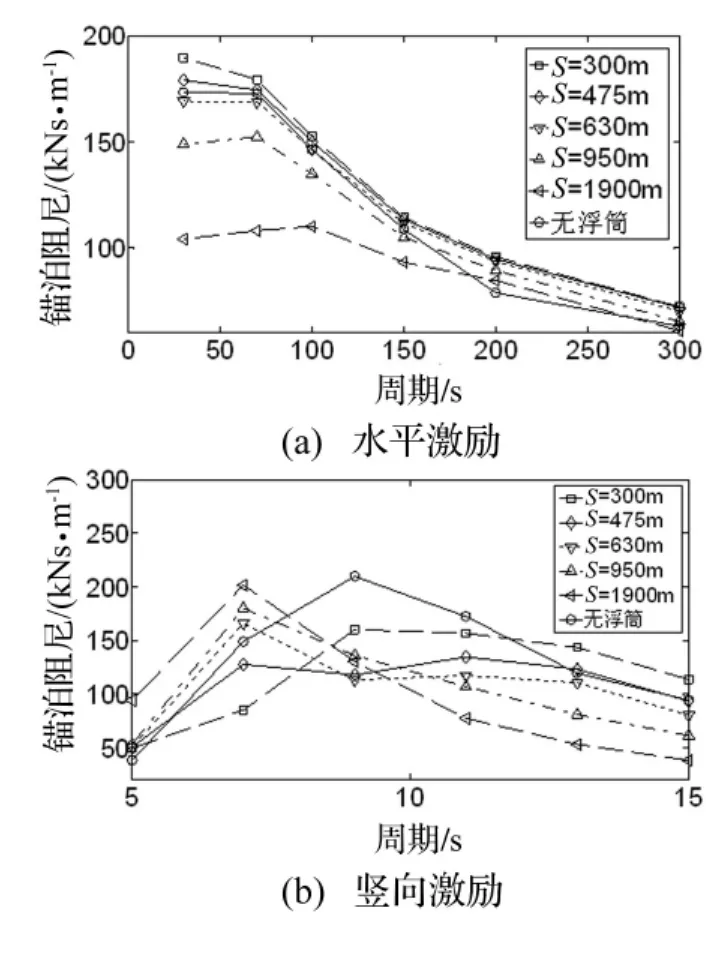
图11 锚泊阻尼(浮筒II)Fig.11 Mooring damping(Buoy II)

图12 锚泊线顶端最大动张力(浮筒III)Fig.12 Maximum dynamic tension at the top(Buoy III)
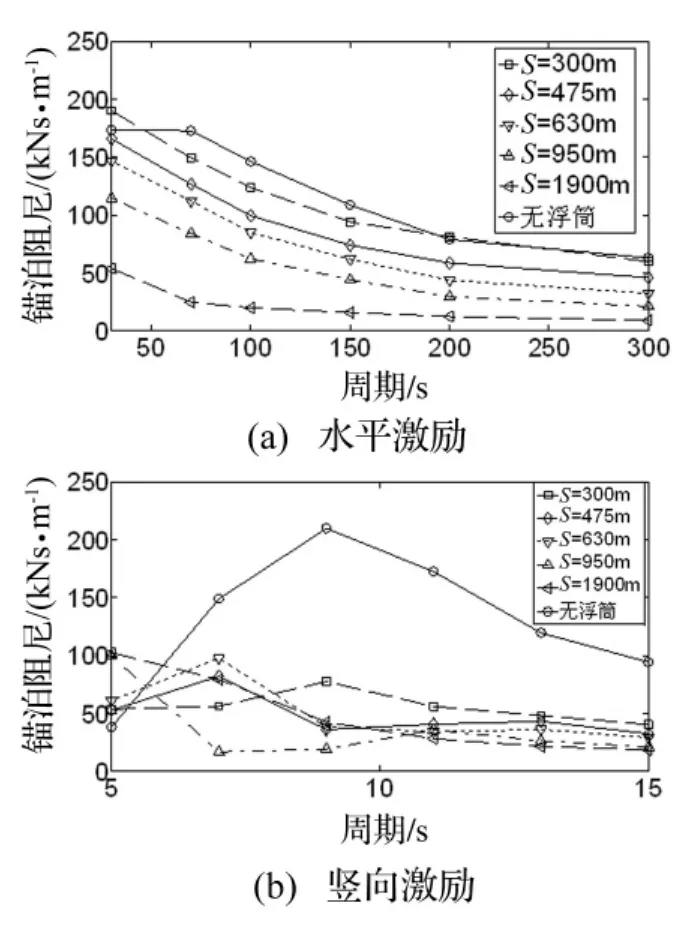
图13 锚泊阻尼(浮筒III)Fig.13 Mooring damping(Buoy III)
5 结论
通过对深水锚泊线串联浮筒系统的动张力和锚泊阻尼变化规律进行计算,并分析了浮筒大小和位置变化的影响,可以得到以下一些结论:
(1)在锚泊线顶端水平激励下,其顶端动张力随着激励周期的增加而呈递减趋势;在锚泊线顶端竖向激励下,其顶端动张力随着激励周期的增加总体呈先增加后递减的趋势。
(2)串联浮筒系统降低了锚泊线顶端的最大动张力,且随着浮筒浮力的逐渐增加,动张力逐渐降低。
(3)随着浮筒所处位置S逐渐向锚固点靠近时,其动张力降低程度逐渐变大。
(4)串联浮筒系统降低了锚泊阻尼的贡献,这对上部平台的运动响应会造成不利的影响,因此在设计锚泊线串联浮筒系统时,需要进行详细的计算和选取。
[1]Nakajima T,Motora S,Fujino M.On the dynamic analysis of multi-component mooring lines[C]//Offshore Technology Conference.Houston,Texas:OTC,1982.
[2]Mavrakos S A,Papazoglou V J,Triantafyllou M S,et al.Experimental and numerical study on the effect of buoys on deep water mooring dynamics[C]//Proceedings of the 1st International Offshore and Polar Engineering Conference.Edinburgh,United Kingdom:ISOPE,1991.
[3]Mavrakos S A,Papazoglou V J,Triantafyllou M S,et al.Deep water mooring dynamics[J].Marine Structures,1996,9:181-209.
[4]Mavrakos S A,Chatjigeorgiou J.Dynamic behaviour of deep water mooring lines with submerged buoys[J].Compurers&Srrucrures,1997,64(14):819 -835.
[5]王冬姣.索-链-浮子/沉子组合锚泊线的静力分析[J].中国海洋平台,2007,16(5):16-20.WANG Dong-jiao.Static analysis of a wire-rope-chainbuoy/sinker mooring line[J].China Offshore Platform,2007,16(5):16-20.
[6]王道能.浮筒锚泊系统受力分析及其仿真[D].哈尔滨:哈尔滨工程大学,2008.
[7]Kwan C T,Bruen F J.Mooring line dynamics:comparison of time domain,frequency domain,and quasi-static analyses[C]//Offshore Technology Conference.Houston,Texas:OTC,1991.
[8]Berteaux H O.Buoy Engineering[M].New York:Wiley Interscience Publication,1976.
[9]赵腾伦.ABAQUS6.6在机械工程中的应用[M].北京:中国水利水电出版社,2007:244.
[10]Qiao D S,Ou J P,Wu F.Design selection analysis for mooring positioning system of deepwater semi-submersible platform [C]//Proceedings of the 22nd International Offshore and Polar Engineering Conference.Rhodes,Greece:ISOPE,2012.
[11]Chaudhury G, Ho C Y. Coupled dynamic analysis of platforms,risers,and moorings[C]//Offshore Technology Conference.Houston,Texas:OTC,2000.
[12]乔东生,欧进萍.深水悬链锚泊线阻尼计算[J].振动与冲击,2011,30(2):24-31.QIAO Dong-sheng,OU Jin-ping.Damping calculation of a deepwater mooring line[J].Journal of Vibration and Shock,2011,30(2):24-31.

