计算多体系统动力学中引入多体系统离散时间传递矩阵法的混合算法研究

高浩鹏，黄映云，赵建华，孙宇鹏

(海军工程大学 船舶与动力学院，武汉 430033)

随着计算机技术特别是计算机应用机技术的发展，人们对于复杂机械系统的多体动力学建模与求解成为可能。目前以多体系统为研究对象的方法主要有两种:需要系统总体动力学方程的传统多体系统动力学方法［1］和无需系统总体动力学方程的多体系统传递矩阵法［2］。这两种方法都是对机械系统中的机构进行研究，虽然都从经典力学发展而来，但这在建模和求解时都具有自己的特点。

建模是多体系统动力学分析的第一步，建模的合理性与准确性直接影响计算结果，鉴于此本文拟结合计算多体系统动力学与多体系统离散时间传递矩阵法，形成一种混合算法。该算法主要将两种算法进行互补，一定程度上扩展了研究对象的内容，也进一步提高了建模精度。

1 研究背景

对于复杂机械系统，若构件间的拓扑关系较为明确，在三维实体建模的基础上，使用计算多体动力学建模分析较为方便，人为因素引起的建模差异较小，易于求解［3］。随着计算机技术，特别是计算机应用技术的迅速发展，人们的研究对象也趋向于复杂机械系统［4］;然而复杂机械系统存在有大量非线性因素、多学科耦合，特别是存在有大量的非确定性因素，这样使得以物理实体建模为基础的多体动力学分析就比较困难。

柴油机结构复杂，整个工作过程涉及多部件的大空间运动，包括平动、转动以及平动和转动的合成运动，其适合通过计算多体动力学建模及分析;然而整个柴油机结构中存在有大量的螺栓连接结构，而大量研究结果表明螺栓连接结构复杂，影响其动力学特性因素较多，很难准确建立其模型进行特性分析［5］。柴油机结构中有很多如缸盖螺栓连接这种受力较大的结合面，如果简单地使用刚性连接必然会对整个柴油机特性产生影响，所以在通过多体动力学对柴油机进行建模时，螺栓连接结构就成了建模的难点。

为了解决多体动力学中螺栓结合面建模问题，须引入人为控制的数值计算方法，然而数值计算方法的引入需以结合面的特性参数为依据。对于如螺栓这种复杂结合面的动力学特性，很难通过建立其实体模型得到;为了较为准确得到其动力学特性就必须结合试验的方法。现代测试技术的发展，使得通过试验得到螺栓结合面动力学特性参数成为可能。故本文的目的就是研究一种结合实体建模和数学建模的方法解决上述问题，该方法要易于通过目前应用软件实现。本文提出计算多体系统动力学与多体系统离散时间传递矩阵法混合算法来解决上述问题。

2 算法研究

原则上讲，计算多体动力学和多体系统传递矩阵法能单独进行大多数机械系统动力学分析;然而这两个方法的建模原理以及求解算法有一定差异，导致各自方法具有自己的特点。为了充分发挥不同方法在相关方面的优势，便研究其混合算法，该算法要易于在目前较为流行的多体动力学分析软件中实现。下面通过分别对这两种算法进行论述的基础上，引出本文所提出的混合算法。

2.1 计算多体动力学方法

计算多体动力学由经典力学发展而来，目前发展到刚柔混合多体系统动力学［1］。根据其建模方法的不同主要分为两种方法:拉格朗日法和笛卡尔法。多体动力学笛卡尔数学建模方法起源于机械领域，由于该建模方法有利于计算机数值求解，目前在应用软件中多采用该方法建模［3］。

下面主要对多刚体系统动力学建模及求解理论进行概述。通过应用软件在建立多体系统模型时，每个构件具有如式(1)所列举的15个变量和如式(2)所列举的15个方程。

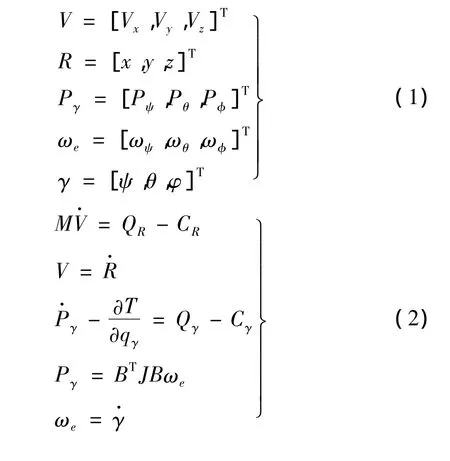
式(1)和式(2)中各参数的含义见附录，由式(1)可知其变量为平动速度、笛卡尔位置坐标、转动惯量、角速度及欧拉角坐标。根据牛顿第二定律、位移与速度的微分关系、带拉格朗日乘子的拉格朗日第一类方程以及转动惯量定律等可以得到如式(2)所示的微分－代数方程。机械系统中每个刚体构件就是通过式(1)建立动力学方程，在此基础上通过构件间的约束力构成构件间作用关系，再建立系统的边界条件，便构成了整个系统的动力学方程。建模与求解过程如图1所示。该方法的优点是:基于物理实体建模，整个模型精度高，易于软件实现可视化界面;刚柔混合多体动力学的发展对柔性体特性分析较易;整个建模过程人为控制因素少，分布式建模方便。缺点是:整个实体建模工作量大;建立的微分方程存在高阶次，求解速度较慢，求解过程可能由于方程的病态而不能计算。

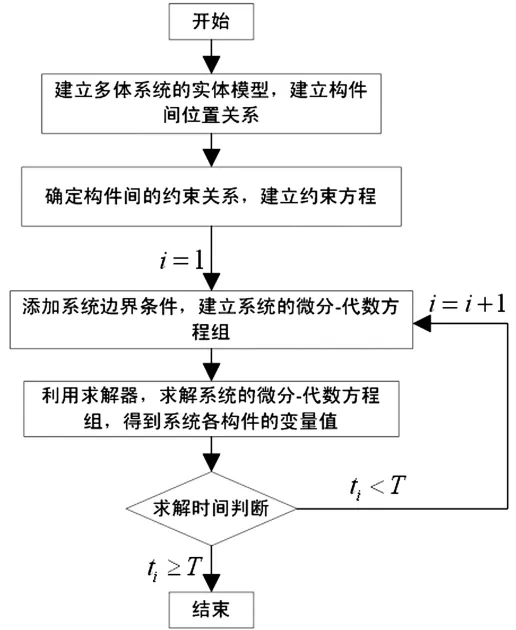
图1 计算多体动力学建模与求解流程图Fig.1 The modeling and solving flow chart of computational dynamics of multi－body systems

2.2 多体系统离散时间传递矩阵法

多体系统传递矩阵法是用传递矩阵研究多体系统动力学的方法，其研究对象是以各种方式相联结的多个构件组成的多体系统，涉及兵器、航空航天、机械等多种行业。根据所研究对象的特性不同其主要有线性多体系统传递矩阵法和多体系统离散时间传递矩阵法［6］。线性多体系统传递矩阵法解决线性多体系统振动问题［7］。多体系统离散时间传递矩阵法主要解决时变、非线性、大运动、受控等一般多体系统动力学问题［8］。

双眼矫正视力差值与远立体视呈负相关性（r=-0.673，P＜0.001），与RDS测得的立体视锐度、交叉立体视、非交叉立体视均呈负相关性（r=-0.439、-0.466、-0.451，P＜0.001）。

下面主要论述多体系统离散时间传递矩阵法的求解过程。多体系统离散时间传递矩阵法的理论较为简洁，即通过传递矩阵关联系统输入状态与输出状态矢量，如式(3)所示;其中Z为状态矢量，U为传递矩阵。传递矩阵由具体结构抽象得到多个力学特征元件并按规则拼装而成，故其重点和难点主要集中在对系统传递矩阵的研究。状态矢量是一个单列阵，表示研究系统中一节点的力学状态;该矢量一般由该点的位置坐标、角坐标、内力以及内力矩组成。

本文研究重点为算法，故对传递矩阵的研究不作为重点，整个求解过程如图2所示。该方法的优点是:无需建立系统的总体动力学方程，易于结合试验数据进行数学建模;由传递矩阵建立的方程阶次较低，计算量小，计算速度快，计算过程不易产生病态。缺点是对研究系统结构进行抽象，传递矩阵的建立具有一定难度，对数学知识要求高，人为因素影响较大;在动力学分析时很难对于柔性体构件的动力学特性进行分析，而且对于构件自身不同部位的特性分析较为困难。

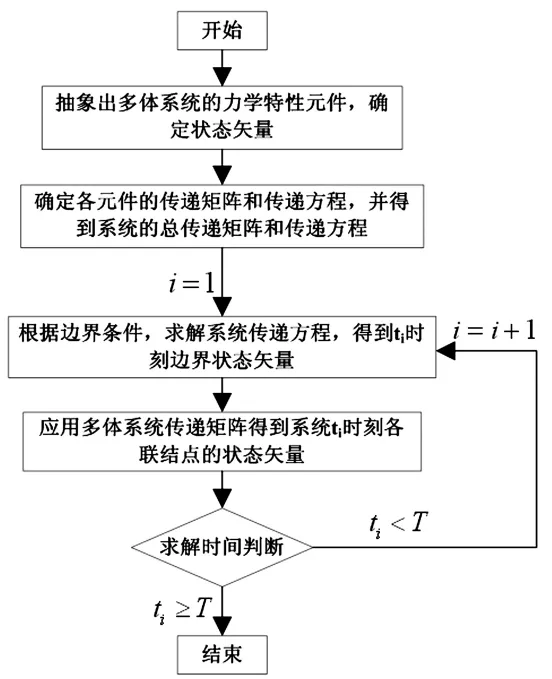
图2 多体系统离散时间

2.3 混合算法

多体动力学和多体系统离散时间传递矩阵法的研究对象都为多体系统，在对这两种方法优缺点分析的基础上引出混合算法，其特点主要是:在多体动力学分析软件基础上，引入多体系统离散时间传递矩阵法，实现可视化的建模，易于对系统进一步优化及特性分析，并且建模过程中人为因素较小，基于实体模型准确度高;多体系统离散时间传递矩阵法的引入，使得复杂子系统特别是具有不确定因素的子系统建模趋向于数学建模，再通过试验确定传递矩阵的参数，其模型精度较高，并且建模和求解过程无需系统总体动力学方程。

在多体动力学软件中引入多体系统离散时间传递矩阵法的建模及求解过程如图3所示。混合算法是在各自子系统建模的基础上研究的，故其研究的重点和求解的可行性集中在两个子系统建模与求解的结合处。对于多体子系统其一般将力/力矩作为边界条件，其求解一般容易得到上文中论述的15个变量;多体系统离散时间传递矩阵法一般将位置和力/力矩作为状态矢量。故混合算法是将多体子系统求解得到的位置量作为多体系统离散时间传递矩阵法的输入与输出状态矢量的已知部分，再通过求解多体系统离散时间传递矩阵法所建立的代数方程得到状态矢量中的内力和内力矩，再将内力和内力矩作为多体系统与多体系统离散时间传递矩阵子系统连接处的力/力矩边界条件添加到多体系统中进行求解得到位置量，这样循环计算便使得计算得以延续，这点便是混合算法的核心。在多体动力学中，这种混合算法可以通过用户子程序进行实现［9］。

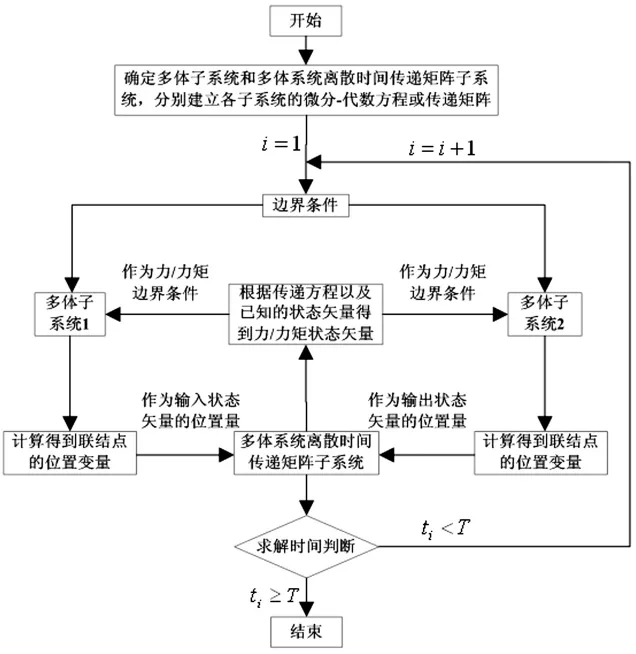
图3 混合算法建模与求解流程图Fig.3 The modeling and solving flow chart of hybrid algorithm

3 算例

螺栓连接结构大量存在于柴油机结构中，影响螺栓结合面特性的因素较多，而且很多因素具有不确定性，故本文以螺栓连接两个刚体的结构为例来使用混合算法对其建模与求解。

3.1 建模

本文在多体动力学分析软件中建立的混合模型如图4所示。多体子系统1中刚体受到向上的外力，多体子系统2中刚体与大地固定，文中将螺栓结合面简化为4个多体系统离散时间传递矩阵法中弹簧－阻尼器典型元件，分别位于多体子系统1的四个角上，并对称分布。

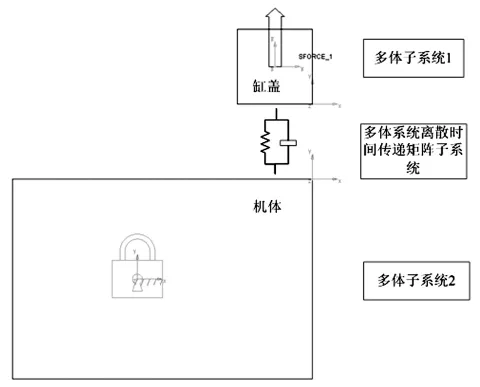
图4 混合模型Fig.4 The hybrid model

对每个子系统进行孤立的分析:多体子系统1的边界条件为外力以及多体系统离散时间传递矩阵子系统对其作用力;多体子系统2的边界条件为地面约束力以及多体系统离散时间子系统对其作用力;多体系统离散时间传递矩阵子系统主要由传递矩阵连接其输入和输出状态矢量。由参考文献［8］可得到单向弹簧－阻尼器的传递方程，拓展后得到三向弹簧－阻尼器的传递方程如式(4)所示，其状态矢量为 Z=［x，y，z，qx，qy，qz，1］T，下标 OUT 表示输出状态矢量、IN 表示输入状态矢量，传递矩阵中各参数的含义见附录。本文通过Fox－Euler法进行线性化，故传递矩阵中的参数已知或者为迭代过程中上个时刻的函数，其传递矩阵中相关线性化系数如式(5)所示。

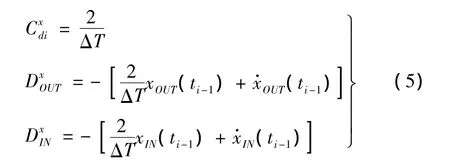
根据文中提出的混合算法，由多体子系统得到多体系统离散时间传递矩阵子系统中状态矢量的位置量，然后通过传递方程求解得到多体系统离散时间传递矩阵子系统中状态矢量的内力和内力矩量，故可以将式(4)变形为式(6)，以便于线性方程组求解。所以混合算法建立模型求解的迭代算法为:求解多体子系统1和多体子系统2，分别得到式(6)中增广矩阵系数中的参数 xIN、xOUT、yIN、、yOUT、zIN、zOUT以及线性化系数中上一时刻的位置和速度量，再加上已知的刚度和阻尼系数，即已知式(6)中所有增广矩阵系数所涉及的参数;将这些参数代入式(6)便可以求解得到多体系统离散时间传递矩阵子系统中输入和输出的状态矢量、和，之后将这几个量作为多体子系统1和多体子系统2的已知边界条件并进行求解，依次循环计算直到设定时刻。

整个建模过程中，多体子系统通过可视化实体建模实现，建立了微分－代数方程组;多体系统离散时间传递矩阵子系统通过用户自定义程序实现，并嵌入到多体动力学分析软件中，进而建立线性代数方程组。混合算法中用户定义子程序的编写是难点，其主函数的格式为“VOID_FUNCTION VFOSUB(int*id，REAL*time，REAL*par，int*nPar，BOOL*dflag，BOOL*iflag，REAL*value)”，其中所涉及的主要问题有:用户定义参数包括刚度、阻尼系数、求解步长以及子系统之间连接点的标识，这些参数通过par变量实现从多体动力学到用户定义子程序的传递;由式(6)可知其增广矩阵形式较为简单，但为了方法的适用性以及增强混合算法的可执行性，本文选取全选主元高斯消去法求解式(6)的线性方程组;式(6)增广矩阵系数中涉及到的上一时刻的位置和速度量通过静态内存变量的定义来实现。

3.2 结果分析

模型建立之后，在多体动力学分析软件中进行求解，其中求解时间1 s、求解步长0.001 s。多体子系统施加的外力如图5所示，其幅值为1 000 N。当4个弹簧－阻尼器的刚度和阻尼系数都为500 N/mm和0.1 N·s/mm时，4个连接点处状态矢量的力和位移值相等，分别如图6中实线和虚线所示。由图6可知，联结点处力状态矢量的幅值为261 N，大于系统施加外力幅值的四分之一，并且其有一定的振荡衰减，这都是由于刚度和阻尼的影响。

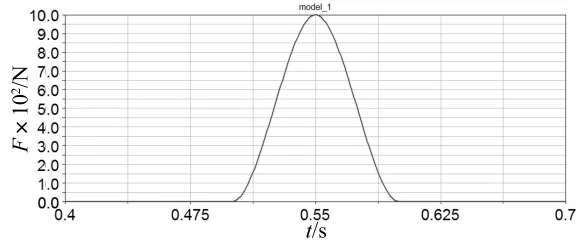
图5 外力边界条件时间历程曲线Fig.5 The boundary condition of external force

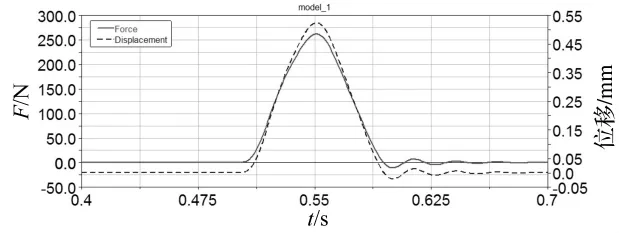
图6 力和位移状态矢量时间历程曲线Fig.6 The force and displacement state vector curves

螺栓连接结合面实际结构复杂，四个螺栓的等效刚度和阻尼很难相等(如由于预紧力大小不一致，或者螺栓结构上细小区别等所导致)。文中假设其中一个刚度小于其它三个刚度20%，则该弹簧－阻尼器处的力状态矢量如图7中实线所示，图中虚线为相邻弹簧－阻尼器的力状态矢量曲线;图8为四个联结点处加速度曲线。由结果分析可知，刚度较小的弹簧－阻尼器联结点处其力状态矢量幅值较相邻联结点处小，并且其大小与对角联结点处相等，验证了实际在拧紧螺栓时按对角顺序拧紧，也验证该方法的正确性;由图8知，虽然只有一个弹簧－阻尼器的刚度有变化，但四个联结点处的加速度在幅值和相位上都有一定的影响。

图7 力状态矢量对比曲线Fig.7 The contrast curves of force state vector

图8 加速度对比曲线Fig.8 The contrast curves of acceleration

混合算法的研究主要是解决一些难于通过实体建模来模拟其结构的子系统，而该子系统对整个动力学特性有一定的影响，该算法的优点是继承了计算多体动力学和多体系统离散时间传递矩阵法各自的优点:在可视化实体建模的基础上，可以得到整个动力学分析模型较为精确的边界条件;难于实体建模的子系统可以通过多体系统离散时间传递矩阵法实现，只需建立该子系统的传递方程即可。文中重点对算法进行研究，故所列举算例较为简单，选取了弹簧－阻尼典型元件作为混合算法研究对象;当然，在多体动力学中该典型元件也可按照弹性连接的方式添加，但其与混合算法有质的区别:多体系统离散时间传递矩阵法的引入是建立代数方程组实现，而弹性连接是建立微分－代数方程组实现。混合算法并不仅仅局限于将弹簧－阻尼元件引入到计算多体动力学中，其可以将所有多体系统离散时间传递矩阵法中典型元件以及典型元件的组合结构引入到计算多体动力学中，即混合算法的实现拓展了多体系统动力学的研究对象。

4 结论

本文以计算多体动力学和多体系统离散时间传递矩阵法建模及求解理论为依据，提出了在多体动力学中引入多体系统离散时间传递矩阵法的混合算法，并以柴油机结构中大量存在的螺栓结合面为算例通过混合算法进行建模与求解。文中算例较为简单，目的主要是论证混合算法的可行性与正确性;在基于实际结构分析时，传递矩阵中的参数应基于试验数据，以保证建模的准确性。

混合算法在多体动力学分析软件中实现，其特点是:结合物理实体建模与数学建模，提高了模型的准确性;多体系统离散时间传递矩阵法的引入结合试验可以建立一些难以通过物理实体模拟的结构，一定程度上扩展了研究对象，并且结合试验数据提高了分析结果的可靠性;混合算法无需建立系统总体动力学方程并且便于分析传递矩阵中特性参数对整个系统动力学的灵敏度，便于结构优化，一定程度上减小了实体建模的数据量。

［1］洪嘉振.计算多体系统动力学［M］.北京:高等教育出版社，1999.

［2］芮筱亭，贠来峰，陆毓琪，等.多体系统传递矩阵法及其应用［M］.北京:科学出版社，2008.

［3］陈立平，张云清，任卫群，等.机械系统动力学分析及ADAMS应用教程［M］.北京:清华大学出版社，2006.

［4］熊晓燕.复杂机械系统动态特性分析和试验辨识方法的研究［D］.太原:太原理工大学，2008.

［5］毛宽民，黄小磊，田红亮，等.机床固定结合面参数识别及其拟合方法［J］.华中科技大学学报(自然科学版)，2011，39(3):18－21.MAO Kuan-min，HUANG Xiao-lei，TIAN Hong-liang，et al.Identifying dynamic parameters of fixed joints in machine tools and its fitting method［J］.Huazhong Univ.of Sci.＆Tech.(Natural Science Edition)，2011，39(3):18 －21.

［6］Rui X T，He B.Advanced in discrete time transfer matrix method formultibody system dynamics［M］.IUTAM Symposium onMultiscaleProblemsin MultibodySystem Contacts，Stuttgart，Germany，2006.

［7］芮筱亭，王国平，贠来峰，等.某远程多管火箭振动特性研究［J］.振动与冲击，2005，24(1):9 －12.RUI Xiao-ting，WANG Guo-ping，YUN Lai-feng，et al.Study on the vivration characteristics of LRMLRS［J］.Journal of Vibration and Shock，2005，24(1):9 －12.

［8］杨富锋.基于多体系统传递矩阵法的工程系统的动力学及其应用［D］.南京:南京理工大学，2006.

［9］邢俊文，陶永忠，译.MSC.Software.MSC.ADAMS/View 高级培训教程［M］.北京:清华大学出版社，2004.

附 录

符 号

V平动速度矢量 QR平动广义力

Vx，Vy，Vz平动速度矢量的三个分量 CR平动约束反力

R位移矢量 Qr转动广义力

x，y，z位移矢量的三个分量 Cr转动约束反力

Pγ广义动量矢量 B坐标变换矩阵

Pψ，Pθ，Pφ广义动量矢量的三个分量 z状态矢量

ωe角速度矢量 q状态矢量中力分量

ωψ，ωθ，ωφ角速度矢量的三个分量 K 刚度

γ角位移矢量 C阻尼

ψ，θ，φ 角位移矢量的三个分量 Cdi、DO、DI线性化系数

M质量矩阵