基于模糊树的Hammerstein-like 模型对超磁致伸缩作动器的建模与控制
张 伟,柳 萍,刘青松,张 臻,毛剑琴,周克敏
(1.北京航空航天大学 自动化科学与电气工程学院,北京 100191;2.路易斯安那州立大学 电气与计算机工程系,巴吞鲁日 70803,美国)
超磁致伸缩作动器具有推进力大、应变大以及响应速度快等优点,用于超精密定位、飞机机翼的精密调节以及结构的主动振动控制中,在航空航天、国防以及国民加工等领域获得了广泛的应用。然而,超磁致伸缩作动器在输入输出关系上存在着复杂的迟滞非线性特性,严重影响了系统的控制精度,甚至造成系统的振荡,因此,对磁致伸缩作动器的迟滞非线性建模具有重要的工程意义。磁致伸缩作动器的迟滞非线性特性与系统的输入信号的频率有关,当系统输入信号的频率发生变化时,迟滞环的形状也随之改变,即表现出率相关性。图1给出了不同频率输入信号下超磁致伸缩作动器的迟滞环。
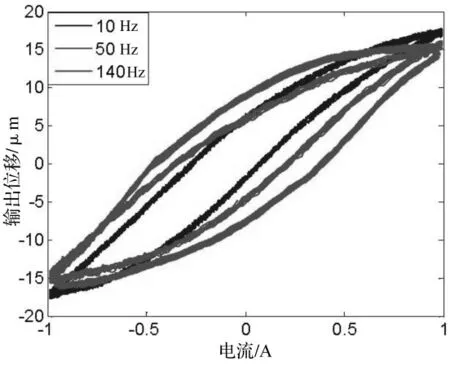
图1 超磁致伸缩作动器在不同频率下的迟滞环Fig.1 Rate-dependent hysteresis
传统的率无关模型,如 Preisach模型[1]、Prandtl-Ishlinskii(PI)模型[2],已不再适用。继而一些学者在J-A模型[3]和Preisach模型等基础上提出改进的率相关建模方法[4-7],但由于模型的物理机理和结构复杂,参数难以确定等约束,限制了模型的应用范围。相比之下计算智能方法机理和所建的模型结构简单,因此寻找基于计算智能的率相关迟滞建模方法,受到越来越多的学者的关注[8-9]。
本文提出一种新的智能化建模方法,用带有动态非线性环节的Hammerstein-like模型描述超磁致伸缩作动器的率相关迟滞非线性特性。该方法采用模糊树拟合非线性环节,因为所建模糊树模型是动态模型,能够描述一定的率相关特性,因此所提模型与传统Hammerstein模型结构相同,但包含了非线性动态环节,为区别,所提模型称为Hammerstein-like模型[10]。
传统的Hammerstein模型是由一个静态无记忆非线性环节串联一个动态线性环节G(z)构成,其背景是被控对象本身近似线性,但是执行机构具有近似静态非线性的情况。许多实际非线性系统都可以用Hammerstein模型来表示,该模型已被用在很多的领域,例如:非线性滤波,饱和激励、声音图像处理、信号分析、生物系统以及化学过程等[11-13]。其结构如图2所示,图中的u(t)和y(t)分别是测试输入和系统输出,v(t)是中间输入信号,实际过程中是不可测量的。

图2 Hammerstein非线性动态模型Fig.2 The structure of Hammerstein model
由于动态线性系统的辨识算法已经较为成熟,Hammerstein模型辨识的研究目前主要集中在非线性环节的拟合上,主要有多项式方法[14-16]、正交基函数[17]、分段线性化[18-19]、神经网络[20]、最小二乘支持向 量 机[21-23],模 糊 聚 类[24-25]等 方 法。 模 糊 树 方法[26-29]是毛剑琴等提出的基于二叉树结构的T-S模糊模型辨识方法(FT),其主要思想是根据输入输出数据的分布自适应划分输入空间,然后将输入空间分段线性化,用隶属度函数将各分段线性函数光滑连接,最后得到一个精度比较高的非线性映射。该方法的优点是建模精度高且在很大程度上缓解了“维数灾”引起的“规则爆炸”,能有效处理高维输入输出数据建模问题。目前,据我们所知,尚无人采用模糊树方法拟合Hammerstein模型的非线性环节,也尚无人采用Hammerstein模型描述超磁致伸缩作动器的率相关迟滞非线性特性。
本文所提建模方法在一个给定的频率范围内建立一个统一的模型,使之不仅适用于单一频率输入信号,也同样适用于复合频率输入信号。建模仿真结果表明,建模精度能满足工程要求。另外,基于所提Hammerstein-like模型,设计一种前馈逆补偿+PID反馈控制策略,实现了超磁致伸缩作动器的跟踪控制实验,实验结果表明了该控制策略的有效性。
1 模糊树方法
模糊树方法[26-29]根据数据样本的分布情况自适应划分输入空间且对输入数据维数不敏感。输入空间的划分情况可以与一棵二叉树T来对应。在每一个叶节点t对应的子空间上,用n维超平面yt(x)=(ct)Tx^逼近非线性函数,其中=[1,xT]T∈Rn+1。如果逼近误差满足要求,则停止对该子空间的划分。对子空间划分的判别函数取为超平面gt(x)=(ct)Tx^-θt=0,其中θt为该子空间上输出数据的重心。模糊树辨识方法根据gt(x)≥0和gt(x)≤0,可以将该子空间划分为两个更精细的子空间,并在gt(x)≈0的区域定义模糊带,最终完成对输入空间的模糊划分。
模糊空间划分完毕,即可得到如下一组规则:

Rl:如果x是Ntl,那么tl∈为叶节点集合,其中~ctl]T∈Rn+1为线性参数,Ntl是模糊子空间χtl上定义的模糊集合,对应的隶属度函数记为Ntl(x)。若将Ntl(x)的归一化隶属度函数记为 μtl(x),即 μtl(x)=,则得到模糊树模型的输出表达式:

二叉树每个节点上的隶属度函数按如下方式定义:(1)对于根节点,

(2)对于非根节点t,
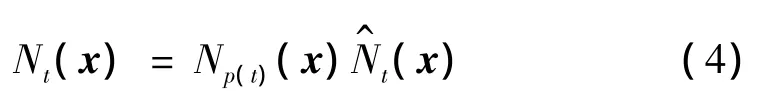
具体的模糊树模型的建模步骤见文献[26-29]。
2 基于模糊树的Hammerstein-like模型对超磁致伸缩作动器的建模
2.1 建模步骤
所提Hammeratein-like建模方法采用模糊树拟合模型中的非线性环节,所建Hammerstein-like模型能统一描述一定频率范围内的迟滞环。建模步骤如下:
算法1:
Step 1)任意给定某单一频率为f的正弦输入信号,所得GMA的输入输出数据为(x(k),y(k),k=1,2,…,M。采用该数据用模糊树方法对GMA建模,用所建动态模型代替Hammerstein-like模型中的非线性部分。Step 2)采用Matlab命令idinput产生一定频率范围内的正弦扫描信号作为GMA的输入信号,用步骤1)中所建模糊树模型计算出中间变量v(k),用v(k)作为线性动态部分的输入,用正弦扫描信号对应的GMA输出数据作为线性动态部分的输出,辨识线性动态系统的参数。
注释1:为了解决迟滞环的多值性问题,建立如下超磁致伸缩作动器的离散动态模型:
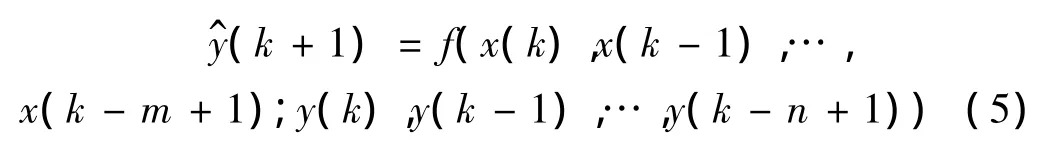
其中:x(k)和y(k)是作动器在时刻k的输入和输出,y^(k+1)表示k+1时刻模型的输出。m和n表示输入和输出的动态阶数。该模型的本质使用作动器当前时刻和历史时刻的输入与输出信息,来预测下一时刻的输出。式(5)表示的动态模型的输入向量包含了历史时刻的输入输出,所以实际上隐含了作动器输入从一个状态到达另一个状态的过程信息,因而可以唯一地确定出当前时刻的输出。仿真实验表明动态阶数m和n对建模误差和检测误差都有影响。折衷考虑建模精度和检测误差,选动态阶数m=n=3。建立动态模型为:
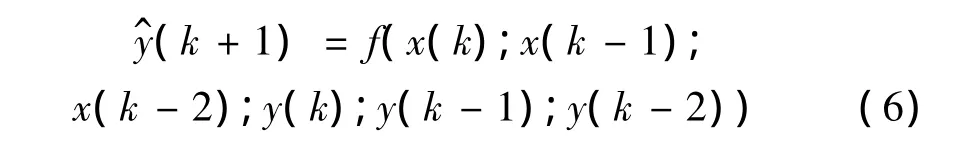
注释2: 步骤1)中的单一频率f可以在正弦扫描信号的频率范围内任意选取。所提Hammerstein-like模型建模的主要思想是:采用某一单一频率下的迟滞环不能很好地描述其他频率下的迟滞环,采用该单一频率下的迟滞环串联辨识得到的线性系统共同描述其他频率的迟滞环。值得指出的是,采用模糊树方法建立的单一频率的迟滞环模型是动态模型,能够描述一定的率相关迟滞特性。这点正是所建Hammersteinlike模型与传统Hammerstein模型的不同之处。
2.2 模型验证
本文采用如图3所示的由北京航空航天大学材料学院研制的超磁滞伸缩作动器[30]。图中主要的部件分别为:
TbDyFe杆:超磁致伸缩作动器的核心部件,提供输出力与位移;
预压装置:紧固螺钉和弹簧,通过调整紧固螺钉11的位置,可以调整弹簧2的预压力,从而获得较好的性能。超磁致伸缩材料在不同预压条件下,其伸长变化线性区间的长度和斜率都不同,其趋势为压力增加则曲线斜率增加。为获得较大的线性段,在作动器中考虑预压装置实现对磁致伸缩材料的预压;
激励线圈:为超磁致伸缩芯棒产生交变的驱动磁场;
永磁体:为TbDyFe芯棒提供一个附加偏置磁场。
建模的训练输入数据和检测输入数据均来自于实验。用GF-20放大器驱动GMA,用电涡流传感器测量得到GMA的位移,dSPACE(DS1103)是用来产生输入信号和确定输出数据采样时间的,采样频率为10 kHz。

图3 超磁滞伸缩作动器Fig.3 Giant magnetostrictive actuator
选取建模步骤1)中的单一频率 f=5 Hz,测得8 000对输入输出数据对,记式(6)中模型的输入为uk=[x(k);x(k-1);x(k-2);y(k);y(k-1);y(k-2)]T∈R6,输出为k=y(k+1),这样可由实验得到的8 000对数据对产生7 997 对训练样本(uk,y^k),k=3,4,…,7 997,将该训练样本作为模糊树方法建模的输入输出数据。取模糊规则数为4,模糊带的宽度α=0.01。步骤2)中正弦扫描信号的频率范围为0~150 Hz。辨识得到的动态线性系统为:G(z) =,所建Hammerstein-like模型如图4所示。

图4 GMA的Hammerstein-like模型Fig.4 The constructed Hammerstein-like system of GMA
为检验所建Hammerstein-like模型的有效性,采用一定频率范围内的GMA的输入输出数据来检验。输入信号为正弦信号,频率分别为10 Hz,30 Hz,…,150 Hz共计8个单一频率和5个复合频率:20/40 Hz,20/40/60 Hz,20/40/60/80 Hz,20/40/60/80/100 Hz和10 ~100 Hz(10 Hz,20 Hz,…,100 Hz的复合)。其中复合频率信号是由若干个不同频率和幅值的正弦信号叠加形成,该信号驱动功率放大器作用于GMA上。对于率相关的迟滞非线性系统,在一个频率段的复合频率的信号可以激励其在一个频率段的率相关特性。采用均方根误差(RMSE)和相对误差(RE)作为评价指标。表1给出所建模型对不同频率的迟滞环的检验结果。从表1可以看出单一频率下的均方根误差的最大值为0.904 4,相对误差均小于7.7%。所建模型能有效地描述0~150 Hz范围内的单一频率下的迟滞环和复合频率下的迟滞环。图5为建模所得的迟滞环与实验数据所得到的迟滞环的比较图。而图6给出的是不同频率输入信号下Hammerstein-like模型的中间变量与实验数据所得的迟滞环的比较图,检验仅仅采用所建立的单一频率下的迟滞模型,即Hammerstein-like模型的非线性部分,描述其他频率下的迟滞环的效果。从图5和图6可以看出,采用单一频率的迟滞模型无法很好地描述其他频率下的迟滞环,而所提Hammerstein-like模型可以很好地描述。

表1 所建Hammerstein-like模型的均方根误差和相对误差Tab.1 RMSE and RE of Hammerstein-like system
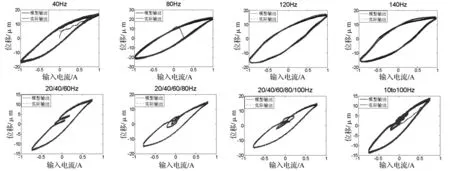
图5 模型检验(实线:建模得到的迟滞环;虚线:实验测得的迟滞环)Fig.5 Model validation(solid:the output of the Hammerstein-like model;dashed:GMA output)

图6 模型检验(实线:Hammerstein-like模型的中间变量;虚线:实验测得的迟滞环)Fig.6 Model validation(solid:the internal variable of the constructed Hammerstein-like model;dashed:GMA output)
为说明步骤1)中的单一频率f可以任意选取,图7给出了采用不同f时所得Hammerstein-like模型在不同单一频率下的迟滞环的检验均方根误差和相对误差曲线。
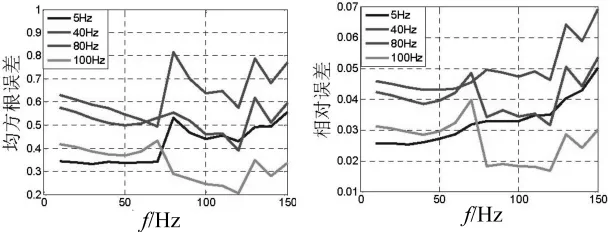
图7 不同单一频率f下的均方根误差和相对误差曲线Fig.7 The influence of f to the RMSE and RE at different single frequencies
从图5可以看出,模型的输出与实验测得的输出基本上重合,说明所建的Hammerstein-like模型能较好地反映作动器对单一频率和复合频率输入信号的迟滞非线性特性。同时,步骤1)中单一频率f的任意选取对建模结果的影响不大。
3 控制器的设计
基于所建模型,采用前馈逆补偿+PID反馈控制的控制策略进行正弦输入信号的跟踪控制实验,图8为控制框图,其中N-1表示非线性部分的逆模型,其建模方法仍采用模糊树。G^是辨识出的动态线性部分G的近似逆,因为G是最小相位系统,因此我们取G^=z-1G-1(z)。
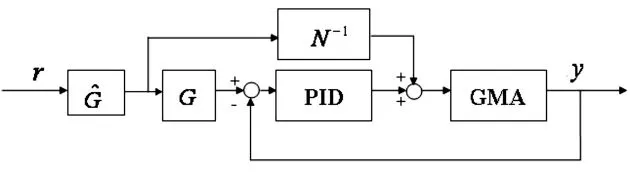
图8 控制框图Fig.8 Block diagram of controller
跟踪控制实验系统示意图如图9所示,实物图如图3所示,超磁致伸缩作动器固定于大质量基座上,电涡流传感器用以测定作动器的输出端位移,GF-20型功率放大器用以为超磁致伸缩作动器提供放大能源,控制程序下载于dSPACE1103控制卡中,并同时实现输入输出信号的采集功能,系统参数的调试由安装于上位机的Controldesk实现,实验采样时间为10 kHz。
跟踪效果检验:跟踪信号为正弦信号,频率为10 Hz,20 Hz,…,150 Hz共计15个单一频率和4个复合频 率:10/30 Hz,10/30/50 Hz,20/40/60/80 Hz,20/40/60/80/100 Hz。PID控制器的参数为kp=1.1,ki=0.5,kd=0.000 01,其中 Kp为比例系数,kt为积分时间常数,kd为微分时间常数。图10给出了频率为40 Hz和100 Hz,幅值为10 μm的正弦参考信号的跟踪实验结果。图11给出了复合频率为10/30/50 Hz和20/40/60/80/100 Hz,幅值为10 μm的复合频率参考信号的跟踪实验结果。表2给出了四次独立实验结果相对误差的平均值。图12是四次独立实验结果单一频率输入信号跟踪结果的相对误差曲线趋势。从跟踪结果可以看出,实际输出能有效跟踪参看输入信号,相对误差均小于15%,跟踪精度令人满意,满足实际工程要求。
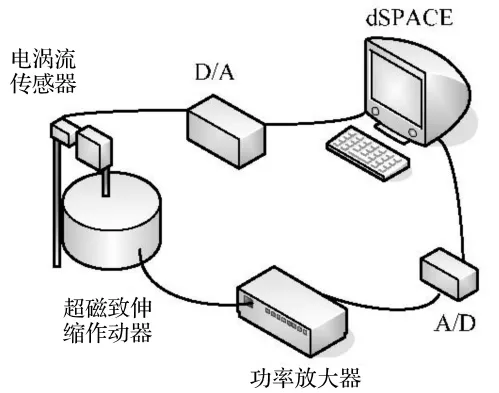
图9 控制系统示意图Fig.9 Control system
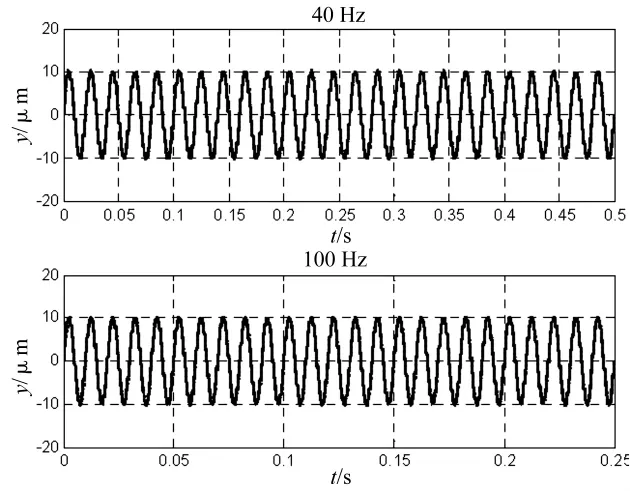
图10 单一频率正弦信号的跟踪结果(实线:参考输入信号;虚线:实际输出)Fig.10 Tracking control results of single frequency(solid:input;dashed:output)
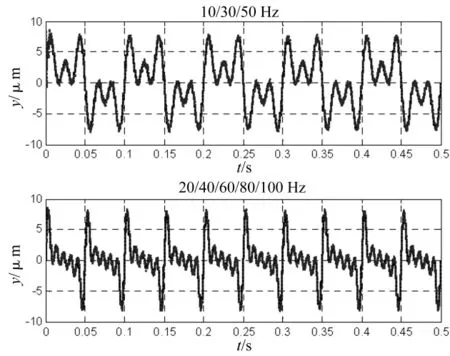
图11 复合频率参考信号的跟踪结果(实线:参考输入信号;虚线:实际输出)Fig.11 Tracking control results of multiple frequencies(solid:input;dashed:output)

表2 跟踪结果的相对误差Tab.2 RE of tracking control results
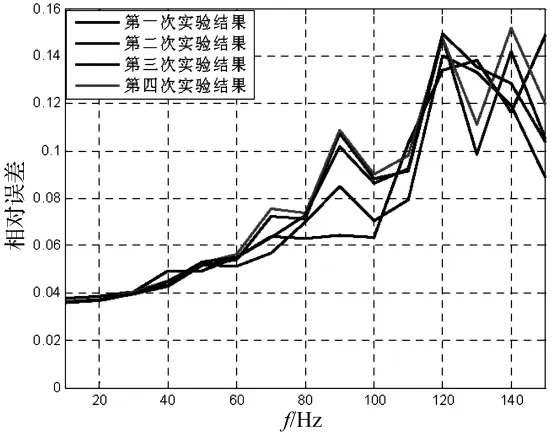
图12 单一频率下相对误差曲线Fig.12 The curves of RE at different single frequencies
4 结论
本文提出一种模糊树的Hammerstein-like模型建模新方法。在给定的频率范围内的单一频率和复合频率,只需要建立一个统一的模型。所提方法具有很好的精度。基于所提模型设计前馈逆补偿+PID反馈控制策略,能较好地跟踪频率范围为1~150 Hz的参考输入信号,跟踪精度令人满意,满足工程要求,为在线建模和主动振动控制提供了一条可供选择的途径。
[1]Mayergoyz.Mathematical models of hysteresis and their Applications[M].Elsevier,2003.
[2]Brokate M,Sprekels J.Hysteresis and phase transitions.springer verlag[M].New York,1996.
[3]Brokate M,Sprekels J.Hysteresis and phase transitions[M].Springer Verlag,New York,1996.
[4]Tan X,Baras J S.Modeling and control of hysteresis in Magentostrictive actuators[J].Automatica,2004,40(9):1469-1480.
[5]Su C Y,Wang Q,Chen X,et al.Adaptive variable structure control of a class of nonlinear systems with unknown Prandtl-Ishlinskii hysteresis[J].IEEE Trans.on Automatic Control,2005,50(12):2069-2074.
[6]Mayergoyz I D.Dynamic preisach model for hysteresis[J].IEEE Trans Mag,1988,24(6).
[7]Klaus K.Modeling,Identification and compensation of complex hysteresis nonlinearitise a modified prandtl-Ishlinskii approach[J].Europen Journal of Control,2003,9(4):407-418.
[8]Lei W,Mao J Q,Ma Y H.A new modeling method for nonlinear rate-dependent hysteresis system based on LS-SVM[C]. The 10th InternationalConferenceson Control.Automation,Robotics and Vision Hanoi,Vietnam,December 2008:1442-1446.
[9]Nealis J M,Smith R C.Robust control of a magnetostrictive actuator[J].Proceedings of SPIE Smart Structures and Materials,2003,5049:221 -232.
[10]Rochdi Y,Giri F,Gning J B,et al.Chaoui,Identification of block-oriented systems in the presence of nonparametric input nonlinearities of switch and backlash types[J].Automatica,2010,46(5):864-877.
[11]Fruzzetti K P,Palazoglu A,McDonald K A.Nonlinear model predictive control using Hammerstein models[J].Journal of Process Control,1997,7(1):31 -41.
[12]Pearson R K,Pottmann M.Gray-box identification of blockoriented nonlinear models[J].Journal of Process Control,2000,10(4):301-315.
[13]Eskinat E,Johnson S H,Luyben W L.Use of Hammerstein models in identification of nonlinear systems[J].AIChE Journal,1991,37(2):255 -268.
[14]Zhu Y.Identification of Hammerstein models for control using ASYM[J].International Journal of Control,2000,73(18):1692-1702.
[15] Westwick D, Kearney R. Separable leastsquares identification of nonlinear Hammerstein models:application to stretch reflex dynamics[J]. Annals of Biomedical Engineering,2001,29(8):707-718.
[16]Pawlak M. On the seriesexpansion approach to the identification[J].IEEE Transactions on Automatic Control,1991,36(6):736-767.
[17]Liu Y,Bai E W.Iterative identification of Hammerstein systems with piecewise-linear nonlinearities[C].Proceedings of the 2006 American Control Conference.Minneapolis Minnesota,USA,June 2006:2357-2362.
[18]Vanpelt T H,Bernstein D S.Nonlinear systems identification using Hammerstein and nonlinear feedback models with piecewise linear static maps[J].Proceedings of American Control Conference.Chicago:IEEE,2000,1(6):225-229.
[19]Voros J.Modeling and parameter identification of systems with multi-segment piecewise-linear characteristics[J].IEEE Transactions on Automatic Control,2002,47(1):184 -188.
[20]Duwaish H A,Karim M N. A new methodforthe identification of Hammerstein model[J].Automatica,1997,33(10):1871-1875.
[21]Espinoza M,Suykens J A K,Demoor B.Partially linear models and least squares support vector machines[C].Proceedings of the 43rd IEEE Conference on Decision and Control.Atlantis,Bahamas:IEEE,2004:3388 -3393.
[22]Goethals I, PelckmansK, SuykensJA K, etal,Identification of MIMO Hammerstein models using least squares support vector machines[J].Automatica,2005,41(7):1263-1272.
[23]Chen K,Wang H Q,Song Z H.A recursive method of identification of Hammerstein model based on least squares support vector machines[C].Proceedings of the 17th IFAC World Congress.Seoul:Elsevier,2008:4993 -4998.
[24]Jia L,Chiu M S,Ge S.A noniterative neuron-fuzzy based identification method for Hammerstein processes[J].Journal of Process Control,2005,15(7):749 -761.
[25]Jia L,Chiu M S,Ge S,et al.Adaptive neuron-fuzzy identification method of Hammerstein model[C].Proceedings of the 2004 IEEE Conference on Cybernetics and Intelligent Systems,Singapore,December 2004:937 -942.
[26]Mao J Q,Zhang J G,Yue Y F,et al.Adaptive treestructured-based fuzzy inference systems[J]. IEEE Transactions on Fuzzy Systems,2005,13(1):1-12.
[27]丁海山,毛剑琴,林 岩.基于模糊树模型的间接自适应模糊控制[J].自动化学报,2008,34(6):666-683.DING Hai-shan,MAO Jian-qin,LIN Yan.Indirect adaptive fuzzycontrolbased on FuzzyTreemodel[J]. Acta Automatica Sinica,2008,34(6):666-683.
[28]张建刚,毛剑琴,夏 天,等.模糊树模型及其在复杂系统辨识中的应用[J].自动化学报,2000,26(3):378-381.ZHANG Jian-gang,MAO Jian-qin,XIA Tian,et al.Fuzzy tree model and its applications to complex system modeling[J].Acta Automatica Sinica,2000,26(3):378-381.
[29]Mao J Q,Ding H S.Intelligent modeling and control for nonlinear systems with rate-dependent hysteresis[J].Science in China Series F:Information Sciences,2009,52(4):656-673.
[30] Zhang T L , Jiang C B,Zhang H,et al.Giant magnetostrictive actuators for active vibration control[J].Smart Materials and Structures,2004,13(3):473 -477.

