一种改进的鱼雷电磁引信目标信号实时小波消噪算法

谭思炜, 任志良, 孙常存



一种改进的鱼雷电磁引信目标信号实时小波消噪算法

谭思炜, 任志良, 孙常存

(海军工程大学 兵器工程系, 湖北 武汉, 430033)

针对Mallat小波变换在算法原理上不具备数据流动性, 无法满足连续采样信号实时消噪处理要求的问题,介绍了一种基于Mallat算法改进的垒墙式小波变换算法, 分析了该算法所具有的数据流动性, 推导了数据流动性与小波分解层数的关系, 并将该算法运用到被加性高斯白噪声污染的鱼雷电磁引信目标信号的实时消噪处理中, 选取双正交样条小波作为小波元, 并对目标信号做两层小波分解与重构。通过MATLAB环境下的仿真试验, 验证了采用该算法实现连续采样信号实时消噪的可行性。消噪后的目标信号具有失真度较小, 波形平滑的特点。

鱼雷; 电磁引信; 小波消噪; 垒墙式算法; 数据流动性

0 引言

复杂的电磁环境严重影响到鱼雷引信动作的可靠性, 容易造成引信误判。对鱼雷目标信号背景噪声中加性高斯白噪声的消噪处理能有效提高引信接收的灵敏度。

小波消噪是一种利用小波变换, 对受噪声污染的目标信号选用适合的小波函数进行分解与重构, 以达到消除噪声的数字滤波技术。小波分析由于同时具有时域分辨率和频域分辨率, 并能根据需要聚焦于信号任意细节的多分辨率特性, 在信号处理领域得到广泛应用。但小波是一种全局分析方法, 小波分解多是采用Mallat塔式算法对数据自顶向下分解, 然后反向重构, 因而处理的数据对象缺乏流动性, 无法实现连续采样信号的实时处理。基于此, 文献[1]提出的基于Mallat塔式算法的改进算法——垒墙式算法, 使得小波分解与重构可按采样数据到达顺序进行, 从而具有实时分析能力。因而可采用该方法, 利用小波消噪的优势, 实现鱼雷电磁引信目标信号的实时消噪处理。

1 目标信号模型

鱼雷主动电磁引信向附近海洋环境发射一定频率的连续电磁波。当鱼雷接近或通过目标时, 引信接收到的目标信号可以用以下方程近似表示[2]

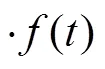
一般情况下, 目标信号的包络可以近似表示为一钟形脉冲, 其经验公式为

综合式(1)和式(2)可得到目标信号

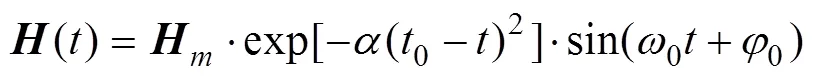
鱼雷目标信号包络示意图如图1所示。

随着鱼雷接近目标, 目标信号包络幅度呈递增趋势。当鱼雷穿过舰船底部龙骨时, 包络幅值出现峰值, 随后随着鱼雷的逐步穿出而递减。

为了让鱼雷能在舰船龙骨底部附近爆炸, 产生最大的杀伤效果, 引信接收机必须对接收到的目标信号进行实时处理。由于目标信号是连续的幅度调制信号, 因而最理想的处理方式应是对目标信号做连续采样、实时消噪以及特征提取。

2 小波消噪

2.1 Mallat算法

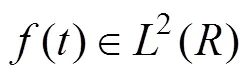
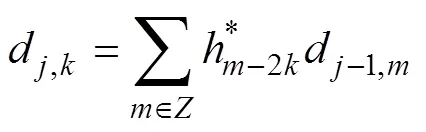
反方向上, 通过综合滤波器得重构算法

Mallat算法可以用如图2所示的双通道分析、综合滤波器组实现。

2.2 消噪思想

小波多分辨率的特性将目标信号在不同尺度下按频率分成不同频段的子信号, 使目标信号中的各种频率成分得到分离, 并为对信号按频带处理提供了条件。

对于信号所在的频段, 小波分解系数得到保留, 对于噪声所在的频段, 按照一定的阈值选取规则(软阈值或硬阈值), 将阈值以下的系数置零, 然后通过小波系数重构波形, 从而达到消噪的目的。

2.3 Mallat算法的局限性

Mallat算法对目标信号做自顶向下的分解, 达到需要尺度后, 自底向上反向重构，因而是一种全局性的数据处理方式, 被处理的数据不具有流动性, 即无法分解与重构按时序输入的数据流, 因而算法上不具有实时处理能力。

文献[4]利用FPGA芯片的高速特性, 从硬件实现上达到了小波实时消噪的目的, 但没有从根本上提高小波算法的实时性。对于连续采样的时序信号, 实际应用中多采用分段处理的方式。这种方式不可避免地在数据截断处产生边界效应[1]。

文献[5]通过首尾截断处部分数据反摺的方法, 一定程度上消除了边界效应, 但对截断处变化较大的信号该方法并不适用。相似的处理方法还有补零法和周期循环法, 但都无法从根本上提高Mallat塔式算法的实时处理能力。

本文着眼于数据流动性，根据数据到达的先后顺序进行处理，从算法原理上讨论Mallat改进算法的实时性。

3 垒墙式算法

3.1 算法原理

实际应用中, 小波变换所使用的尺度函数和小波函数都具有紧支撑性, 这使得用于分析、综合的滤波器也具有紧支撑性, 即滤波器序列长度有限。由图2可知, 目标信号的小波分解, 即是数据序列与分析滤波器序列卷积后取偶数点的结果。分析滤波器序列长度有限, 因而每次卷积计算结果只与数据序列中的部分数据有关。

垒墙算法卷积计算顺序示意图如图3所示, 数据处理过程如图4所示。

图3 垒墙算法示意图

图4 数据处理过程

此外, 由于数据序列的输入是时间连续的, 卷积计算也是连贯的, 因而每段无需再做边缘处理, 计算结果理论上与小波分解的全局计算一致。同理, 小波信号的重构也是通过有限长度的卷积运算实现, 因而同样可采用以上方法实现。

3.2 数据流动性与小波变换层数关系

4 仿真结果与分析

本文采用基于垒墙式算法的实时小波变换, 在MATLAB环境下对受加性高斯白噪声污染的鱼雷电磁引信目标信号模拟实时消噪。考虑接收机对消噪效果和实时性的要求, 本文只对目标信号做2层小波分解与重构。

4.1 小波函数的选择

考虑到鱼雷电磁引信目标信号中含有丰富的相位信息[6], 因而需要减少对目标信号做消噪处理后产生的相位失真。这就要求滤波器的单位采样响应是对称的。双正交样条小波不仅具有对称性和线性相位, 而且滤波器系数有限且均为有理数, 因而适合用作本文对鱼雷目标信号消噪的小波函数。选取滤波器序列长度为8的双正交样条小波, 如图5所示。

4.2 滤波方法的选取

由于默认阈值法具有能得到原始信号的近似最优估计, 计算速度快以及具有广泛适应性的优点[1], 因而在做消噪处理时, 采用默认阈值除去能量明显小于信号的噪声部分。

4.3 仿真结果与分析

目标信号采用式(3)模拟得到, 信号模型如图6所示。噪声采用均值为0, 标准差为1的加性高斯白噪声模型。

当信噪比(signal to noise ratio, SNR)分别为11.8 dB、5.6 dB时, 消噪前后仿真结果如图7、图8所示。经消噪得到的波形平滑, 消噪效果理想。随着SNR的降低, 波形失真度增大, 但目标信号的包络轮廓仍然清晰可见, 包络递增趋势几乎没有失真。

图5 滤波器序列

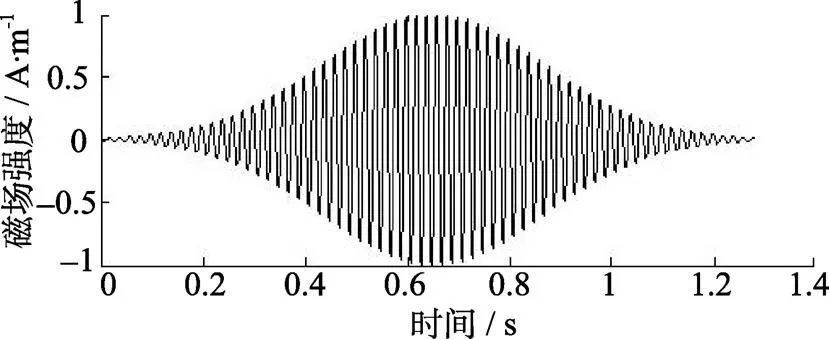
图6 目标信号模型

图7 信噪比（SNR）为11.8 dB时仿真结果

为验证算法的有效性和适用性, 本文在5种相差较大的SNR下, 分别对消噪前后信号的均方根误差(root mean square error, RMSE)进行计算。每组SNR试验记录了30个独立有效的仿真数据, 同组试验数据对应的SNR值相差不超过0.1。为简化描述, 本文将每组SNR下的RMSE求均值。结果对比见表1。

图8 SNR=5.6 dB时仿真结果

表1 不同SNR时均方根误差结果对比

5 结束语

针对鱼雷电磁引信目标信号消噪分析的特点和实时性要求, 采用垒墙式算法, 从算法上解决了Mallat小波变换无法处理连续采样数据, 不具有实时性的问题, 并通过仿真试验验证了采用垒墙式算法实现连续采样信号实时消噪的可行性。仿真结果表明, 该方法消噪效果理想, 消噪后波形失真度小, 能提高鱼雷电磁引信动作的可靠性。

[1] 饶贵安, 康宜华, 陈龙驹, 等．一种新的实时小波分析[J]．仪器仪表学报, 2005, 26(2): 181-183, 205．Rao Gui-an, Kang Yi-hua, Chen Long-ju, et al. A New Meth- od of Real Time Wavelet Analysis[J]. Chinese Journal of Sci- entific Instrument, 2005, 26(2): 181-183, 205.

[2] 王绍卿, 刘健民．鱼雷近炸引信原理与设计[M]．西安: 西北工业大学出版社, 1992．

[3] 胡广书．数字信号处理——理论、算法与实现[M]．北京: 清华大学出版社, 2003．

[4] 蒋行国, 莫少宁, 褚福刚．基于FPGA的信号小波实时处理方法[J]．电子技术应用, 2010, 36(12): 45-47．Jiang Xing-guo, Mo Shao-ning, Chu Fu-gang. Method of Si- gnal Wavelet Real-time Processing Based on FPGA[J]. Application of Electronic Technique, 2010, 36(12): 45-47.

[5] 姚天任, 孙洪．现代数字信号处理[M]．武汉: 华中理工大学出版社, 1999．

[6] 陈光, 任志良．同步检波在鱼雷电磁引信中的应用及仿真研究[J]．计算机仿真, 2010, 27(1): 20-23．Chen Guang, Ren Zhi-liang. Application and Simulation of Synchronous Demodulation in Torpedo Electromagnetic Fuze[J]. Computer Simulation, 2010, 27(1): 20-23.

An Improved Algorithm of Real-time Wavelet Denoising for Target Signal of Torpedo Electromagnetic Fuze

TAN Si-wei, REN Zhi-liang, SUN Chang-cun

(Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China)

The wavelet transform based on Mallat algorithm cannot process flowing data, it is therefore unable to meet the requirement for real-time denoising of continuous sampling signals. As a result, this paper proposes a novel wavelet transform based on Mallat algorithm modification, called bricklaying algorithm. The ability of the proposed algorithm to process flowing data is analyzed, and the relationship between data flowing and level of wavelet decomposition is deduced. The bricklaying algorithm is applied to real-time denoising of torpedo electromagnetic fuze signal in the background of additive white Gaussian noise, where a biorthogonal spline wavelet is taken as the wavelet function, and 2-level wavelet decomposition and reconstruction are performed. The feasibility of the bricklaying algorithm in real-time denoising of continuous sampling signals is verified via MATLAB simulations. The results show that the denoised target signal gains the feature of smooth waveform with smaller distortion.

torpedo; electromagnetic fuze; wavelet denoising; bricklaying algorithm; data flowing

TJ431.7; TN97

A

1673-1948(2013)01-0020-05

2012-06-11;

2012-07-07.

谭思炜(1985-), 男, 在读博士, 研究方向为军用目标特性及其信息处理技术.

(责任编辑: 杨力军)