基于遗传算法的锚固结构外露段动力特性研究

姚 锋，刘方华

（湖南科技大学 土木工程学院，湘潭 411201）

0 引 言

锚固是用埋设在地层中的锚杆把结构物和地层紧紧的联系在一起，依赖锚杆和地层的抗剪强度来传递结构的拉力，使地层自身得到加固，保持结构物与土体的稳定性［1］.和传统的方法相比，锚固特别是预应力锚固有很多特点.梁和板是预应力结构的基本构件，锚具用在端部来对钢筋施加预应力，从而改变结构的力学性能，增加了混凝土开裂强度，提高了结构的变形刚度.因为预应力锚固技术的可靠性、经济性，先进性，人们将它广泛的用于大跨度预应力混凝土连续箱梁桥、采矿巷道支护、隧道地铁支护等大型工程中，而且得到迅速发展.但是，由于受到材料、施工和地质条件等因素的影响，锚固结构在施工与使用过程中存在很多损伤，例如预应力混凝土箱梁桥腹板开裂.为了防止结构发生事故，延长它使用时间，提高工程的可靠性和安全性，我们要对锚固质量和受力状态进行检测［2］.

由于锚固技术在各项工程中使用面宽，并多为隐蔽工程.研究锚固结构外露段的动力特性为锚固质量及受力状态的无损检测技术在大跨度预应力混凝土连续箱梁桥和地下工程等施工和后续监管的质量检测和稳定性评价方面的应用提供了可靠的理论依据.本文的研究不但具有理论价值，并具有广泛的工程使用价值［3］.

1 单自由度振动模型的提出

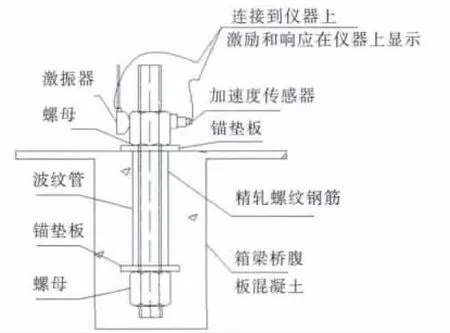
图1 竖向预应力筋简图

在图1中螺母与锚垫板两真实粗糙表面间的接触如图2所示，

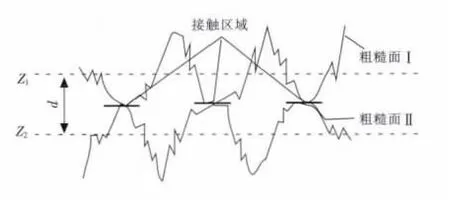
图2 实际接触表面

在水平方向对螺母施加一个瞬态激励时，粗糙表面微凸体的接触点会产生微小的相对线位移和角位移，表现为切向刚度.在法向方向螺母与锚垫板之间存在压力传递，切向刚度与法向荷载存在一一对应的线性关系.因此，在只考虑考虑切向刚度的情况下，视竖向预应力钢筋螺母为一个质量系统，螺母与锚垫板的切向视为弹簧联结，如图3所示，建立基于单自由度的振动模型.

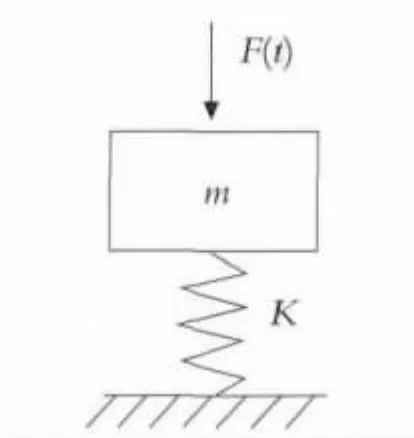
图3 单自由度振动模型

在这个单自由度振动模型中，预应力钢筋、钢筋上端螺母和下端螺母组成一个质量体系，求解时可视为一个广义的质量m，K为切向刚度，F（t）为对上端螺母的水平瞬态激励，瞬态激励由连接在仪器上的激振器发出，在仪器上可读出输入的波形.在螺母的另一端安装有加速度传感器，可接收输出波形.通过研究仪器显示的输入输出波形，利用结构动力学的逆问题来识别单自由度振动模型的系统参数，从而求解切向刚度K.

2 实验模型的建立与试验方案

2.1 实验模型的建立

我们在实验室建立了竖向预应力试验简支梁模型，如图4、图5所示，梁高3.0m，长3.6m，宽1.2 m.支座长1.2m，宽0.5m，高0.6m.布置竖向预应力钢筋，每排5根，共10根.每排每根竖向预应力钢筋的实测间距大约控制在50cm左右.

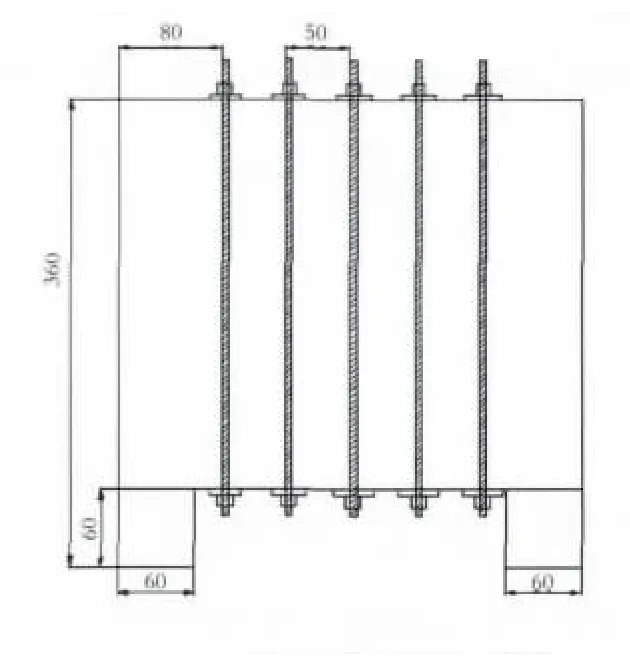
图4 模型正面设计图

图5 模型成品

2.2 试验方案

试验共计应用5根竖向预应力筋，在下端安置的压力传感器精确控制张拉力，从5～45t，5t为一级共9级的分级张拉.在每级张拉后，分别对5根钢筋采集波形，用激振器对螺母的一端进行水平激励，在另一端安装加速度传感器接收响应.

3 K－T曲线的试验研究

3.1 遗传算法辨别系统参数

其中m是系统质量，c为阻尼，k为切向刚度.

所以存在的矩阵方程：

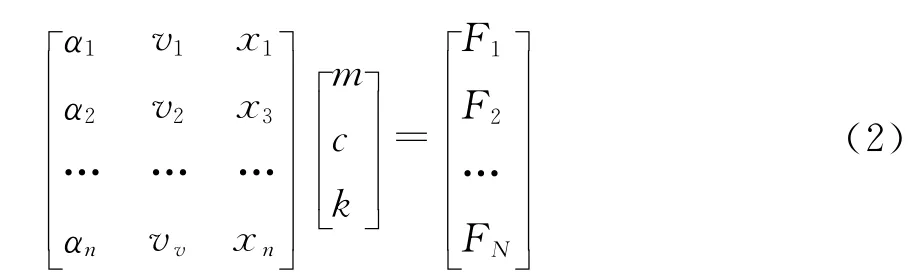
单自由度系统动力参数反演的遗传算法设计思路：根据遗传算法的自适应性，对已经测得的系统动力响应信号，在一定范围内随机选出若干组动力参数m、c、k，代入式（1）中，就可以得到系统的加速度响应函数，且和已经测得的系统加速度响应信号对比，分析比较后选取适应值相对大的动力参数当作父代.将父代进行交叉与变异等一系列操作，又可以获得几组动力参数当作子代，然后进行前面的数值计算，判别适应度函数，如此循环往复.当适应度函数值趋于0时，就能够获得计算结果和原始信号最相近的一组动力参数，就是最优解［4－7］.

遗传算法设计就是确定适应度函数、遗传操作的方法和终止准则.现作如下设计：

（1）确定解的空间范围.系统动力的参数包括系统的质量、阻尼、刚度，它们取决于系统的力学性能与设计参数，本文中全部取1～10.

（2）种群进行随机初始化.

当适应度函数值趋于1时，并且最优子代的适应度值渐渐趋于平均值，计算结果与实测结果接近.

（4）确定遗传操作的方法.本问题使用排序选择，采用单点交叉、算术交叉和启发式交叉进行交叉操作，然后使用非均匀的变异操作来产出下一代.

（5）确定终止准则.终止准则是用来判断程序是否停止的依据，一般可以取最大迭代数（即子代数），本文取100.

3.2 试验结果与分析

在MATLAB窗口中输入gatool，打开进入遗传算法工具.建立适应度函数，用matlab编制适应度函数的程序，再输入变量个数以及3个变量的取值范围，最后用迭代次数（100）作为程序终止准则.

根据图6可以看出，5根钢筋的刚度K在5～40t的不同张拉力下呈线性递增关系，张拉到45t时K值出现负增长.5根钢筋张拉到相同吨位下，K值在较小范围内出现波动，只有张拉到45t时K值出现较大变化，曲线趋势清晰.

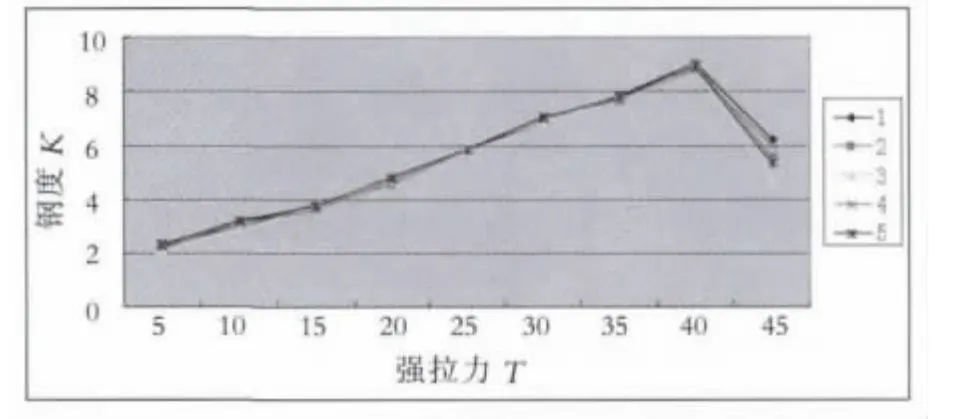
图6 K－T曲线图

4 结 论

本文将竖向预应力筋简化为单自由度振动模型，在实验室建立了竖向预应力试验简支梁模型.用激振器对螺母的一端进行水平激励，用加速度传感器在另一端接收响应.然后用遗传算法进行参数反演程序的设计和编写工作，采用matlab工具箱计算结果.计算结果表明刚度K在5～40t的不同张拉力下呈线性递增关系，张拉到45t时出现负增长，曲线趋势清晰.本文为无损检测技术在锚固结构质量及受力状态上的应用提供了理论依据与参考价值.

［1］熊红霞.桥梁结构模态参数辨识与损伤识别方法研究［D］.武汉理工大学硕士论文，2009.

［2］董清华.地基、结构及其相互作用系统参数识别理论［D］.西安建筑科技大学硕士论文，2004.

［3］秦 莹.基于系统动力响应的锚固结构无损检测及模型试验研究［D］.武汉理工大学硕士论文，2009.

［4］魏连伟，韩文秀.二基于模拟退火遗传算法的水文地质参数识别［J］.天津大学学报，2003，36（5）：618－621.

［5］C.G.Koh，B.Hong，C.Y.Liaw.Substructural and progressive structural identification methods［J］.Engineering Structures，2003，25：1551－1563.

［6］钱炜祺，汪 清，何开锋，蔡金狮.混合遗传算法在气动力参数辨识中的应用［J］.飞行力学，2004（3）：33－36.

［7］袁伟杰，刘贵杰.基于遗传算法的自治水下机器人水动力参数辨识方法［J］.机械工程学报，2010，6：96－100.