基于双剪强度理论下土质隧道自然成拱的最小埋深研究

李腾飞，陈秋南，马晓朋，赵 柳

（湖南科技大学 土木工程学院，湘潭 411201）

近年来，随着我国交通建设的大力发展，隧道成为了其主要修建物之一［1］.隧道在开挖之前，围岩经过长时间的变化过程中已达到平衡状态，而一旦隧道开挖，围岩便会受到扰动，平衡状态就会被破坏，导致围岩应力出现重新分布，而此时隧道的顶部围岩也会不断的塌落，如果隧道埋深足够，围岩塌落到一定程度便会自行停止，这时顶部围岩将形成一个稳定的卸荷拱.如何充分发挥围岩的自承能力一直以来都是隧道工程中的一项重要研究课题，通过研究隧道成拱与成拱埋深之间的关系可以在实际工程中有效的控制围岩变形，防止塌方等事故的发生.关于隧道的成拱机理方面，国内学者也有过一些研究.例如：梁晓丹［2－3］针对隧道拱现象与围岩变形关系进行了分析研究，卢成［4］考虑拱效应研究防冒顶技术等.但是，对于隧道成拱问题的分析及研究，大部分的学者都是基于Mohr－Coulomb强度准则的基础上进行的，由于其理论只考虑了大主应力σ1与小主应力σ3的影响，而忽略了中间主应力σ2，因此，计算结果往往与实际情况存在偏差.本文基于双剪强度理论，考虑了中间应力σ2的影响，比 Mohr－Coulomb强度准则考虑更加全面，计算结果更加精确，为今后此类工程设计计算提供参考及借鉴.

1 基本假设

以下对于隧道开挖而形成的拱模型计算作出2点基本假设：

（1）隧道开挖后，在不受到任何外界荷载的作用下能够自稳成拱；（2）隧道地表处没有任何外界荷载作用，拱部围岩仅仅只受自重W的作用；（3）隧道开挖时，会在左右两侧形成角度为α的破裂面（α＝45°为土体的粘聚力）如图1所示.

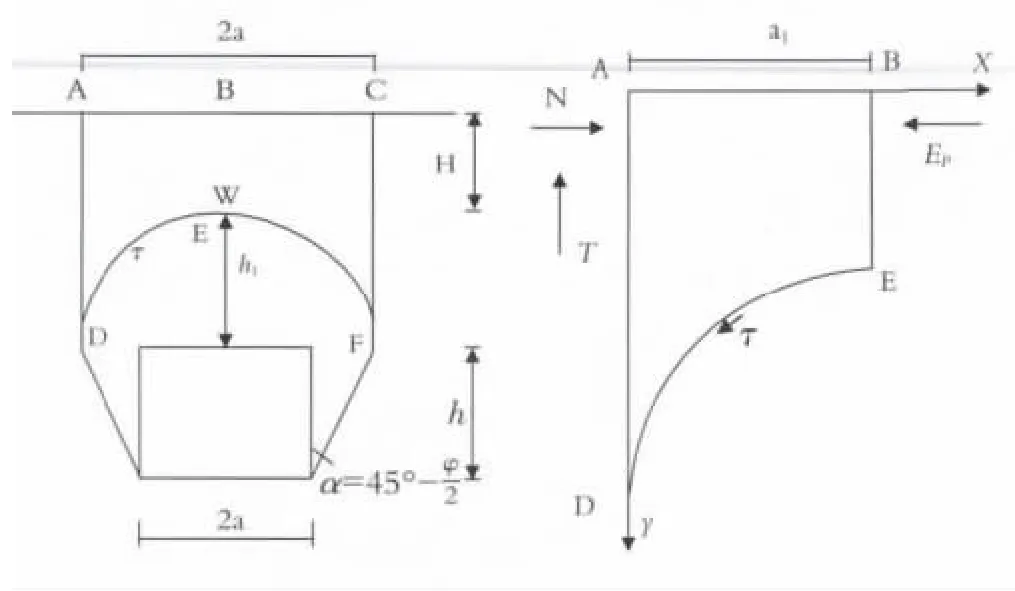
图1 隧道计算拱示意图

2 隧道成拱最小埋深求解

在对隧道进行开挖的过程中，其内部会产生一破裂区域，破裂区内的围岩在受到自身重量的作用下不断向隧道内塌落，当塌落到一定程度时便会自行停止，最终能够在不靠外界荷载的作用下形成一类似椭圆状的卸荷拱（如图1中ABCFED所示）.本文将对形成这一卸荷拱的最小埋深进行求解.

如图1所示，卸荷拱（ABCFED）的重量为W，两侧受到来自土体的水平压力N以及竖直方向的摩阻力T的作用.根据力的对称性原则，以下取卸荷拱的一半进行分析计算.根据文献［5－6］可知，BE面上的剪应力为0，只考虑水平压力N的作用.水平压力N最初为0，而随着隧道开挖的进行，拱效应现象会使得水平压力N不断增大，一直达到某临界值，隧道便趋于稳定，能够自稳成拱，此时的临界土压力值达到被动土压力Ep.此外，BE面上的水平方向为最大主应力方向，即被动土压力Ep的受力方向；竖直方向为最小主应力方向，大小为0，以上因素均满足朗肯被动土压力的所需条件.

对于粘土而言，破裂区表面（DEF）的土体正处在即将塌落的临界状态，在粘聚力c的作用下，对上部破裂区土体会产生大小为τ＝c的剪应力.（本文为偏于安全考虑，则忽略τ的水平分力影响.）

隧道能够自然成拱的必要条件是竖直方向上满足受力平衡条件：

式中：β为破裂区沿线与水平线的夹角，近似取∫τsinβd1≈ch1，α1＝htanα，W为卸荷拱的重量，γ为土体重度.

水平方向满足受力平衡条件：

由Mohr－Coulomb强度理论可得：

综合以上式子可得：

式中：Ep为被动土压力，Kp为被动土压力系数.根据普氏理论可知，隧道成拱高度为f为土体的坚硬系数，为了简化计算同时处于安全考虑，取计算.综合式子（5）、（6）可以得到：

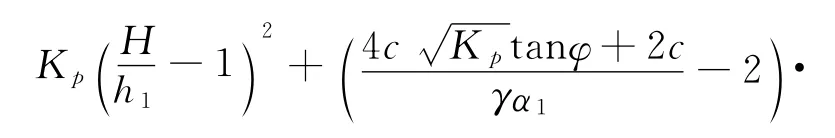
3 基于双减强度理论的求解

双减强度理论的表达式为：

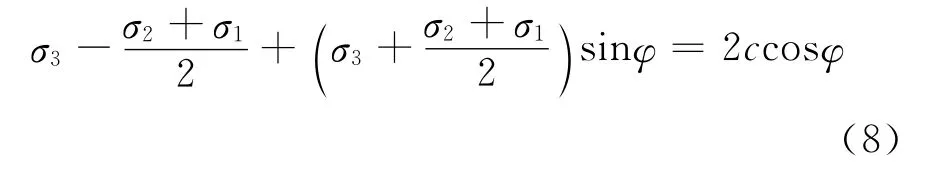
由文献［7－10］可知，令：

注：当土体处于弹性阶段时，m＜1；当土体处于塑形阶段时，m无限接近于1.

将式子（9）代入式子（8）中可得：

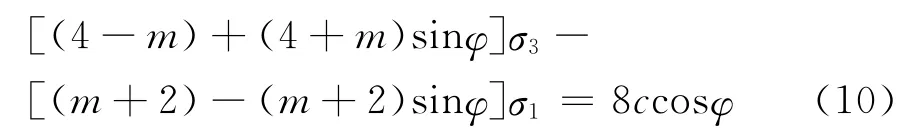
对于式子（10）进行必要的变换，可以得到大主应力σ1与小主应力σ3的相互关系表达式：

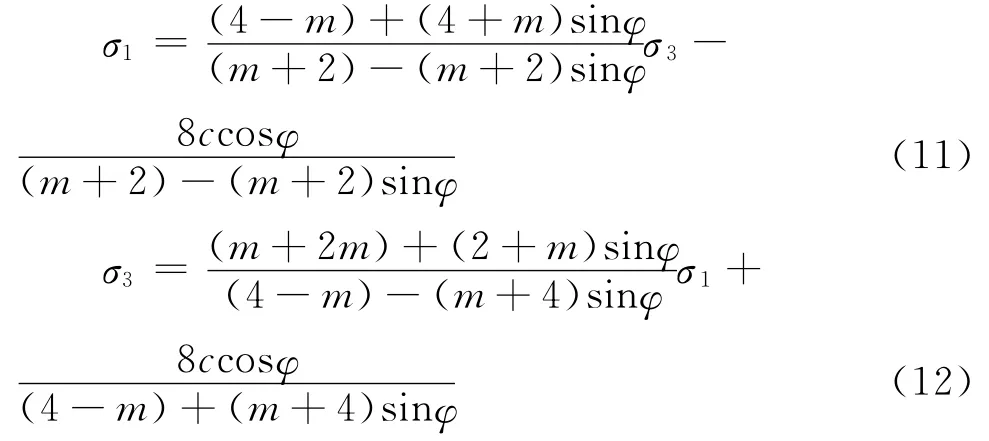
隧道围岩中任意位置Z处的竖向应力大小为σz＝γz，方向竖直向下；而水平应力σx则不断增大直至出现朗肯被动形态，大小则为被动土压力Ep.由上节可知，水平方向为大主应力方向，竖直方向为小主应力方向，因此，式子（12）可以改写成：

最后，将式子（14）、（15）同时代入式子（6）中，可以解出基于双减强度理论下隧道自稳成拱的最小埋深.

4 算例分析

已知云桂先铁路新发一号土质隧道，本隧道位于云南省红河州米勒至石林区段内，设计为12‰单面上坡，全长386m，隧道最大埋深约为30m.具体参数如表1所示.

表1 新发一号隧道参数表

（1）基于Mohr－Coulomb强度理论公式法计算：

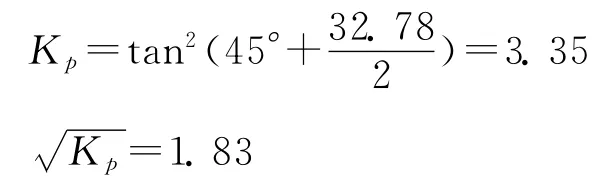
（2）基于双剪强度理论的公式法进行计算（取m＝1）：

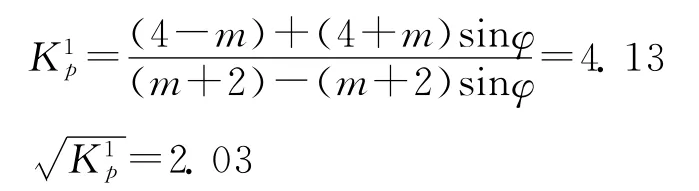
综合以上可知，基于Mohr－Coulomb理论计算出的隧道最小成拱高度为32.5m，比基于双剪理论计算出的隧道最小成拱高度28.7m要大，这是由于后者考虑了中间主应力的作用，计算结果更为精确.而本隧道最大埋深约为30m，因此，在对本隧道进行施工工法的选择上以及采取的支护措施上，可以将此作为参考依据，以避免发生类似于塌方等安全事故，给人们生命及财产造成损失.

5 结 论

基于Mohr－Coulomb强度理论由于只考虑了最大主应力σ1与最小主应力σ3的作用，而忽略了中间应力σ2作用的影响，计算结果往往与实际情况存在差距，而本文基于双剪强度理论计算出来的隧道成拱最小埋深，则弥补了Mohr－Coulomb理论中存在的不足，计算结果更为精确.为类似的隧道工程设计以及施工工法的选择上提供参考依据.

［1］陈秋南.隧道工程［M］.机械工业出版社，2007.

［2］梁晓丹，宋宏伟，赵 坚.隧道压力拱与围岩变形关系［J］.西安科技大学学报，2008，28（4）：647－650.

［3］梁晓丹，刘 刚，赵 坚.地下工程压力拱拱体的确定与成拱分析［J］.河海大学学报，2005，33（3）：314－317.

［4］卢 成，程五一.巷道应力拱成拱及防冒顶技术分析［J］.中国安全生产科学技术，2008，4（6）：114－118.

［5］胡向东，赵俊杰.人工冻结稳定场巴霍尔金模型准确性研究［J］.地下空间与工程学报，2010，6（1）：96－101.

［6］加 瑞.盾构隧道垂直土压力松动效应的研究［D］.南京：河海大学硕士论文，2007.

［7］周小平，哈秋聆，张永兴.考虑裂隙间相互作用下围岩卸荷过程应力应变关系［J］.力学季刊，2002，23（2）：227－235.

［8］罗 汀，姚仰平，松冈元.基于SMP准则的土的平面应变公式［J］.岩土力学，2000，21（4）：390－393.

［9］Kimata T.Uchida K.Hasegawa T.A Considering on the Intermediate Principal Stress of Plane Strain Tests［A］.In：Proc.27th Japan National Conf.On SMFE［C］.1992：693－694.

［10］Matsuoka N.Prediction of Plane Strain Strength for Soils from Triaxial Compression［A］.In：Proc of 10th int，Conf.on Soil Mech.And Found Eng.［C］.Stockholm：［s.n.］，1981：682－683.