滚轮支承卧式离心铸造机横向振动性能分析
李正美,展益彬,安 琦,李柳湘
(1.华东理工大学 机械与动力工程学院,上海 200237;2.卓然设备制造有限公司,江苏 靖江 214537)
滚轮支承的卧式离心铸造机是由两列滚轮支承1根厚壁腔筒组成的转子系统,广泛用于石油工业炉管的制备.在实际生产中,由于铸造机型管或浇铸钢水的偏心质量引起的不平衡响应往往使得卧式离心铸造机产生较大的噪声和较高的产品报废率.为了降低噪声,提高炉管产品的品质,需要准确而细致地分析离心铸造机振动特性进而采取合理的减振措施.
目前分析转子振动特性的方法主要分为有限元法(FEM)和传递矩阵法(TMM).当转子系统的自由度取得较多时,宜采用TMM.文献[1]建立了连续质量转子的传递矩阵但忽略了转动惯量和陀螺效应.文献[2]用传递矩阵法对柔性轴承支承的柔性转子进行了模态分析,计算了有阻尼固有频率.文献[3]把传递矩阵法拓展到了非线性转子系统的振动分析.文献[4]用传递矩阵法对球轴承支承的非对称柔性转子系统进行了瞬态分析.文献[5-6]用传递矩阵法分别分析了对称及非对称转子系统的弯-扭耦合振动特性.文献[7]对未对中及不平衡转子系统的动态特性进行了研究,分析了转子不对中和不平衡量对振动响应和临界转速的影响.
由前人的研究工作可以看出,TMM可用于线性或非线性转子系统的稳态和瞬态振动性能分析,但非线性系统传递矩阵的推导过于复杂.离心铸造机的滚轮由线接触滚子轴承支承,滚轮和型筒间也为线接触,线接触的载荷-位移关系非线性较弱,因而以静态刚度对系统进行线性化处理.此外,铸造机型筒粗长,应考虑转动惯量和对陀螺力矩对转子振动性能的影响.在以往的研究中.也有不少考虑了转动惯量和陀螺力矩,但却忽视了支承偏转刚度的作用.本文对滚轮-型筒法向接触刚度和偏转刚度以及轴承中滚子-滚道法向接触刚度、偏转刚度和法向油膜阻尼进行了分析计算.建立了考虑各支承偏转刚度、阻尼以及各圆盘转动惯量、陀螺力矩的改进型传递矩阵法,对离心铸造机转子系统的固有频率、模态振型以及不平衡响应进行了计算分析.研究了滚轮支承间距对离心铸造机转子系统横向振动性能的影响.
1 离心铸造机结构系统与力学分析
卧式离心铸造机的结构系统和受载情况如图1所示.用于铸造炉管的型筒由2列4个半径为Rw的滚轮支承.2列滚轮沿型筒轴向对称布置,列间距为L2.每列的2个滚轮的中心与型筒中心的连线成一定的支承夹角α.各个滚轮由1对滚子轴承支承在固定于底板的支座上,其中一个滚轮上安装有皮带轮输入动力.
作用于离心铸造机型筒上的静态载荷为型筒的重力(以单位长度型筒的重力来表示)和滚轮的支承力.安装有皮带滚的一个滚轮除了支承一部分型筒重力外还受到皮带拉力F1和F2的作用.由于结构的对称性,各滚轮与型筒的接触载荷相等.单个滚轮轴上的载荷可认为由该滚轮轴上的一对轴承平均分担.

图1 卧式离心铸造机结构系统结构和受载情况Fig.1 Structure system and load condition of horizontal centrifugal casting machine
2 滚轮支承的刚度和阻尼
单个滚轮对型筒法向支承的动力学模型如图2所示.滚轮的质量远小于型筒质量,可忽略不计.因此滚轮与型筒接触时滚轮可等效成具有线刚度Krw和偏转刚度Kθrw的无质量部件,而滚动轴承则等效成具有线刚度Krb、偏转刚度Kθrb和阻尼Crb无质量部件对滚轮轴进行支承.滚轮轴粗短,弯曲刚度很大,可认为是刚性的.
根据Palmgren线接触载荷-位移关系[8],单个滚轮-型筒间的法向接触刚度和偏转刚度分别为

图2 单个滚轮支承的动力学模型Fig.2 Dynamic model of a single rolling wheel supporting the forming cylinder
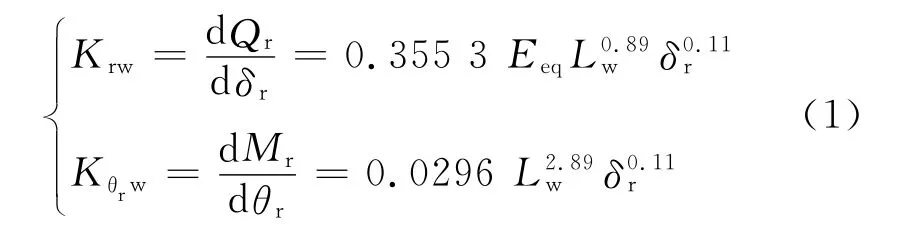
式中:Qr为径向接触载荷;δr为径向相对位移;Eeq为等效杨氏模量;Lw为滚轮与型筒的接触宽度;Mr和θr分别为径向所在的轴平面内滚轮-型筒间的偏转力矩和相对偏转角.
滚子轴承内部包含多个滚子-滚道接触.根据各滚子的位移协调关系和轴承的静力平衡条件可得到轴承的径向刚度和相应轴向平面内的偏转刚度分别为
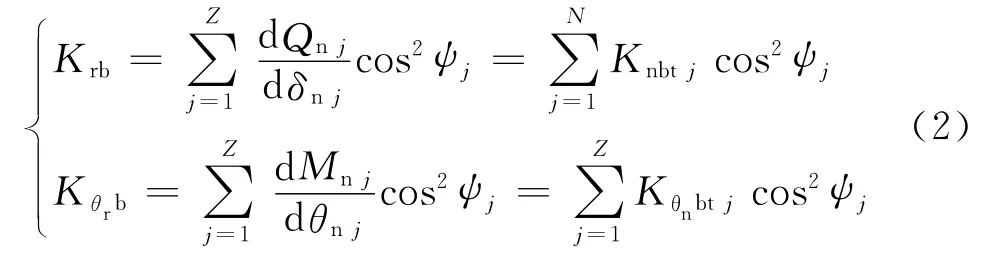
式中:Z为轴承中的滚动体数目;Qn为法向接触载荷;δn为法向相对位移;Mn和θn分别为法向所在轴平面内滚子-滚道间的偏转力矩和相对偏转角;Knbtj,Kθnbtj分别为ψj上内外两滚道间的法向、偏转刚度;ψj为滚子j周向方位角.
轴承中单个滚子-滚道接触的动力学模型如图3所示.图3中:u1和u2分别为两接触表面的滚动速度;uz为z向相对速度;b为Hertz接触半宽;pHertz和pfilm分别表示Hertz接触压力分布和油膜压力分布.滚子-滚道间的法向刚度由弹性接触刚度和油膜刚度串联而成,因此在任一滚子角位置ψj上,内外两滚道间的法向刚度和偏转刚度分别为

图3 单个滚子-滚道接触的动力学模型Fig.3 Dynamic model of a single roller-raceway contact

式中:Kcbij,Kfbij和Kcboj,Kfboj分别为滚子-内滚道接触和滚子-外滚道间的弹性接触刚度和油膜刚度.
单个滚子-滚道接触中的弹性接触刚度Kcb和偏转刚度Kθnb的计算可分别参照滚轮-型筒接触的刚度计算式(1)进行.单个滚子-滚道接触中的油膜刚度Kf可采用杨沛然-温诗铸线接触中心膜厚公式[9]导出为
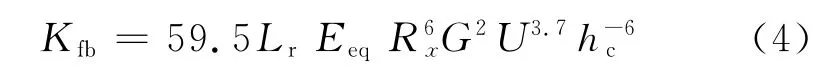
式中:Lr为滚子有效长度;Rx为沿滚子滚道方向上的等效半径;hc为中心膜厚;G和U为润滑分析中常用的Dowson量纲一材料和速度参数.
滚动轴承中一般只考虑油膜阻尼.滚动轴承沿某一径向的整体油膜阻尼也可表示成各个角位置上滚动体-滚道法向油膜阻尼的函数为

式中:Qfnj,unj分别为滚子j的法向阻尼力和法向相对速度.
近似认为滚子与内外滚道间的法向相对速度皆为该滚动角位置上内外滚道间法向相对速度的一半,则在ψj位置上内外滚道间的法向阻尼系数为

式中:Cnbij和Cnboj分别为滚子j与内外滚道接触的法向阻尼系数.
通过对Reynolds方程积分,弹性流体动压润滑状态下单个滚子-滚道接触的法向阻尼系数可表示为

式中:xin和xout分别为润滑入口处和出口处的位置坐标;x为接触区内任意一点沿滚动方向位置坐标;η为与油膜压力p有关的黏度,可由润滑油的黏压关系计算;h为油膜厚度.油膜压力p的分布和油膜厚度h可通过完全数值解法确定.
基于上述有关滚轮-型筒接触刚度以及滚子轴承刚度与阻尼的分析,图2所示的型筒到单个支座间的支承可进一步简化为一个具有线刚度Krs、偏转刚度Kθrs和阻尼Crs的部件.其中:

式中:下标left和right为支承同一滚轮轴的左、右两个轴承.
每列滚轮位置上,型筒与底板间沿x,y方向(见图1)的刚度和阻尼以及绕y,x轴的偏转刚度最终可由Krs,Kθrs,Crs以及相关结构参数表示.
3 离心铸造机横向振动模型
如图4所示,用集总参数法将卧式离心铸造机转子系统离散为带有n个集中质量(节点)的刚性薄圆盘和n-1个无质量的弹性轴段的多自由度系统(未画出xOz平面内的刚度和阻尼).选取位移、转角、力矩和剪力作为状态变量,通过力学分析可建立转子起始和终止两截面状态变量间的传递方程,再根据系统的边界条件即可求出满足该方程的固有频率、模态阵型或强迫振动响应.
对于滚轮支承的刚度和阻尼各向异性的情况,系统的横向振动分析不能简化到单一的轴向平面内进行,而需沿两个正交的方向进行.根据如图5所示的轴段和圆盘在xOz和yOz两个平面内的受力分析,系统的第j个圆盘(质点)的运动方程为

式中:上标L,R分别表示圆盘的左右端截面;下标j表示圆盘或轴段序号;Mx,My分别为xOz和yOz平面内的弯矩;Qx,Qy分别为沿x,y轴的剪力;l为轴段长度;EI为轴段的抗弯刚度.设x=XCeλt,y=YCeλt,θy=ΨCeλt,θx=ΦCeλt,XC,YC,ΨC,ΦC分别为复位移x,y,θy,θx的复振幅,t为时间.对系统的自由振动,取λ=-μ+iωr,对系统的简谐强迫振动,取λ=iωs.μ为阻尼衰减系数,ωr为固有频率,ωs为外部激励频率.
转子系统自由振动时,圆盘上的力矩和剪力增量只与圆盘位移状态变量有关,因而在任意圆盘左右端截面上的状态变量为

式中:Jx,Jy,Jz分别为圆盘绕x,y,z轴的转动惯量;ω为圆盘自转角速度;m为圆盘质量;Krxx,Krxy,Kryx,Kryy,Kθrxx,Kθrxy,Kθryx,Kθryy,Crxx,Crxy,Cryx,Cryy分别为相应的坐标方向及其耦合关系的圆盘上总的外部径向刚度、偏转刚度、径向阻尼.
式(11)中的方阵为轴段上的场传递矩阵,记为Aj,而式(12)的方阵即为圆盘上的点传递矩阵,记为Bj对于图5所示的转子系统有
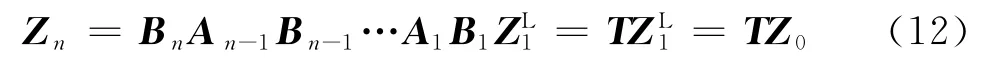
式中:Zn为截面上的状态矢量,Zn=[x,y,ψ,φ,Mx,My,Qx,Qy]T;T为系统的总体传递矩阵.
由转子系统的总体传递矩阵与边界条件可得出系统的频率函数进而求解系统的各阶固有频率ωr和阻尼衰减系数μ.受轴承黏性油膜阻尼和圆盘陀螺力矩的影响,系统的各阶模态为复模态.
对于轴上零件的偏心不平衡量引起的强迫振动,外部激励频率ωs=ω;力矩和剪力增量还包含与圆盘位移变量无关的不平衡量引起的离心力.在考虑了圆盘离心力的情况下,图5所示系统的最右端截面与最左端状态变量的传递关系不能再如式(12)那样以总体传递矩阵的形式表达,但对于简谐的外部激励力,可以通过在复平面内搜索第一个圆盘上的线位移复振幅XC1和YC1以及角位移复振幅ΨC1和ΦC1的值,使最右端截面上的边界条件同时得以满足.这样就可根据式(10)求得各个截面上的强迫振动响应的复振幅.
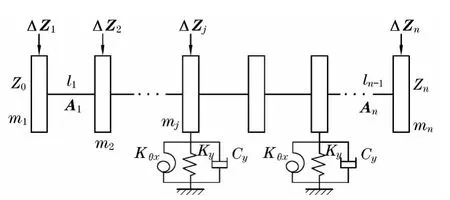
图4 离心铸造机转子系统的离散化Fig.4 Discretization of the rotor system in centrifugal casting machine

图5 轴段和圆盘的受力分析Fig.5 Load analysis of a single shaft and disk
4 实例计算与结果分析
本文以江苏卓然机械股份有限公司的某一型号的离心铸造机为研究对象来分析其转子系统的振动性能.该铸造机相关结构参数见表1.
支承滚轮的滚子轴承型号为NU410,轴承润滑脂基油的环境黏度为0.05Pa·s,铸造机型筒工作转速为2 700r·min-1.由前文所述的计算方法得到单个滚轮-型筒接触、单个滚子轴承以及单列滚轮支承的各方向刚度与阻尼为Krw=3.04MN·mm-1,Krb=1.26MN·mm-1,Kθrb=42.00MN·mm·rad-1,Kθrw=2.53GN·mm·rad-1,Crb=112N·s·mm-1,Ktxx=Ktyy=1.38MN·mm-1,Kθtxx=Kθtyy=2.30GN·mm·rad-1,Ctxx=Ctyy=363N·s·mm-1.

表1 离心铸造机结构参数Tab.1 Structural parameters of the centrifugal casting machine
由于支承夹角α为90°,转子系统退化为对称系统.因同列支承中的2个滚轮对称布置,x和y方向耦合刚度和耦合阻尼均为零值.用前述振动模型计算得到离心铸造机型筒横向振动的前三阶有阻尼固有频率和振动衰减系数如表2所示.作为比较,表2同时给出不计支承偏转刚度时的固有频率和衰减系数.可以看出,该型号离心铸造机的工作转速低于但接近第一阶临界转速(3 302r·min-1),铸造机转子系统的振动将较为显著.此外,支承的偏转刚度对转子系统的各阶固有频率和衰减系数都有一定影响,阶数越低,其影响越显著.

表2 离心铸造机型筒横向振动的前三阶固有频率和衰减因子Tab.2 Natural frequencies and attenuation coefficients of the rotor lateral vibration
由于制造误差和材料的不均匀性,使得离心铸造机的型筒存在一定的偏心不平衡量.图6给出了离心机铸造型筒上不平衡响应的最大振幅随型筒转速的变化曲线.假设型筒沿轴向均匀偏心,偏心距为0.05mm.可以看出,型筒不平衡响应振幅整体上随转速的增加而增大,而当型筒的转动频率与系统的固有频率相近时,不平衡响应的振幅急剧增加,出现共振.
图7表示离心铸造机型筒横向振动的前三阶有阻尼固有频率比(固有频率与L1/Lt=0.2时的固有频率之比)与滚轮支承位置之间的关系.在实际生产中,2列滚轮支承一般都是沿着型筒轴向对称布置的,型筒转速也要求低于1阶临界转速.若用单列支承距离型筒端部的长度与型筒总长的比值L1/Lt来表示支承的轴向位置,可以看出L1/Lt≈0.22时,型筒横向振动的1阶固有频率达到最大值(以L1/Lt=0.2时的固有频率作为参考频率ωr,L1/Lt=0.2).也就是说当型筒转速一定时,此支承位置使得型筒转速最大程度地偏离1阶临界转速,从而减小不平衡响应的振幅值.

图6 离心铸造机型筒的不平衡响应曲线Fig.6 Unbalance response curve of the forming cylinder

图7 滚轮支承的轴向位置对型筒固有频率比的影响Fig.7 Influence of the axial position of rolling wheel on natural frequencies ratio of the forming cylinder
5 结论
(1)在考虑支承偏转刚度、型筒转动惯量和陀螺效应的基础上对传统的传递矩阵法进行了改进,建立更为准确的离心铸造机横向振动模型.
(2)分析了离心铸造机型筒横向振动的有阻尼固有频率、不平衡响应以及滚轮支承的轴向位置对离心铸造机型筒振动特性的影响.研究结果表明,2列滚轮支承的间距约为型筒总长的0.56倍时,型筒横向振动的一阶固有频率最高,不平衡响应最不显著,支承效果最佳.
[1]LUND J W,ORCUTT F K.Calculations and experiments on the unbalance response of a flexible rotor[J].Journal of Engineering for Industry,1967,89:785-796.
[2]BANSAL P N,KIRK R G.Stability and damped critical speeds of rotor-bearing systems[J].Journal of Engineering for Industry,1975,97:1325-1332.
[3]LEE A C,KANG Y,LIU S L.Steady-state analysis of a rotor mounted on nonlinear bearings by the transfer matrix method[J].Int J Mech Sci,1993,35:479-490.
[4]LIEW A,FENG N S,HAHN E J.On using the transfer matrix formulation for transient analysis of nonlinear rotor bearing systems[J].International Journal of Rotating Machinery,2004,10(6):425-431.
[5]HSIEH S C,CHEN J H,LEE A C.A modified transfer matrix method for the coupled lateral and torsional vibrations of symmetric rotor-bearing systems[J].Journal of Sound and Vibration,2006,289:294-333.
[6]HSIEH S C,CHEN J H,LEE A C.A modified transfer matrix method for the coupling lateral and torsional vibrations of asymmetric rotor-bearing systems[J].Journal of Sound and Vibration,2008,312:563-571.
[7]TSAI C Y,HUANG S C.Transfer matrix for rotor coupler with parallel misalignment[J].Journal of Mechanical Science and Technology,2009,23(5):1383-1395.
[8]PALMGREN A.Ball and roller bearing engineering[M].3rd ed.Philadelphia:SKF Industries Inc,1959.
[9]温诗铸,杨沛然.弹性流体动力润滑[M].北京:清华大学出版社,1992.WEN Shizhu,YANG Peiran.Elastohydrodynamic lubrication[M].Beijing:Tsinghua University Press,1992.

