离心-振动试验系统的准连续高阶终端滑模控制方法
王跃钢,左朝阳,2,文超斌,郭志斌
令方程组右端等于零,得到方程唯一解:
离心-振动试验系统因离心机与振动台之间运动存在耦合现象而成为一种不确定非线性系统[1],对于这类复杂的不确定非线性系统采用线性控制理论和设计方法难于进行。而一般对于振动台控制算法的研究大多建立在线性系统的基础之上[2-5],算法的稳定性和收敛速度等方面还需要进一步研究,同时还存在控制精度不高,控制鲁棒性差,操作也不方便等问题。因此,控制算法设计的好坏直接关系到系统的输出模拟过载振动复合环境的精确度。而滑模控制既适用于线性系统,又适用于非线性系统,其算法简单,设计方便,对外部干扰及参数摄动具有强鲁棒性,且有限时间收敛[6]。
然而传统的滑模控制的不连续性会导致所谓的“抖振”现象,且传统滑模控制一般采用线性滑模面设计,系统状态收敛时间趋于无穷,容易造成较大的累积跟踪误差。为了解决无限时间收敛问题,通过在滑模设计中引入非线性函数[7]而产生的终端滑模控制,使得在滑动模态跟踪误差能够在有限时间收敛至零;后来Yu等[8]提出快速终端滑模面进一步提高收敛速度;Feng等[9]针对终端滑模控制中可能出现奇异现象,提出了非奇异终端滑动模态,避免了奇异问题,并在文献[10-11]中基于终端滑模设计方法,提出一种二阶、三阶及高阶终端滑模控制方法,实现了无抖振滑模控制,提高了系统的动态响应速度。同时由于准连续高阶滑模能够有效消除抖振[12-16],获得更高的控制精度;因此本文在文献[14]基础上,根据离心-振动试验系统振动特点,设计基于二阶终端滑模面的准连续高阶终端滑模控制器,在保证鲁棒性和抗干扰性的同时获得连续的控制信号。仿真结果表明,该控制器实现了离心振动试验系统的振动位移控制,能够较好地实现振动位移跟踪,并在有限时间内收敛。
1 高阶滑模控制介绍
定义1:假设滑动模态s沿系统轨迹的微分量s·,存在且为系统状态的连续函数,于是r阶滑动模态集合由下面的等式确定。
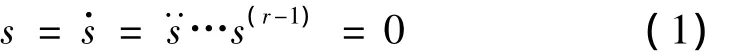
假设r阶滑动模态集合非空且为Fillipov意义下的局部积分集合,则称符合式(1)的运动为基于滑动模态s的r阶滑模,而r定义为系统的滑动阶。
考虑如下非线性仿射系统
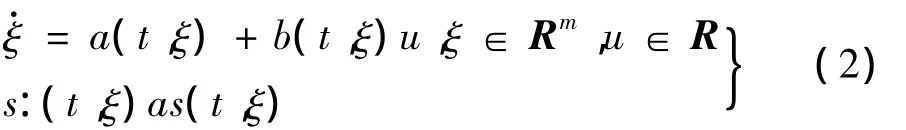
式中:s为系统可测输出量,u为系统控制量,函数a,b,s充分光滑。设系统相对阶为r,式中输出量沿系统轨迹进行r次微分,于是有:
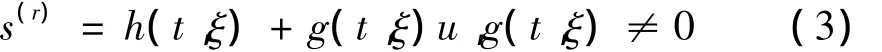
其中:h(t,ξ)=s(r)u=0,g(t,ξ)= ∂ s(r)/∂u。设下述不等式成立
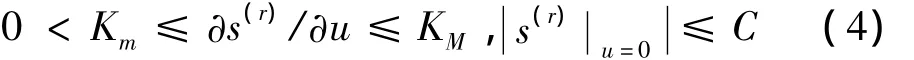
其中:Km,KM,C>0。式(3)~(4)意味着微分包含:
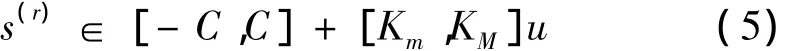
成立。
引理 1[14]:定义
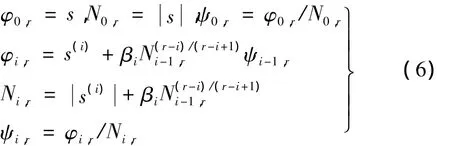
如果恰当选择参数 β1,…,βr-1,α >0,则控制作用(7)将使得系统(2)在有限时间内到达r阶滑模面。
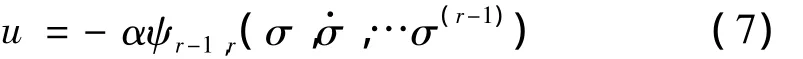
2 离心-振动试验系统准连续高阶终端滑模控制器的设计
2.1 离心-振动试验系统数学模型
离心-振动试验系统是通过将振动台安装在离心机臂臂端来实现的,它以离心机为载体模拟过载环境,通过在其臂端上的振动台模拟振动环境。图1为离心-振动试验系统示意图。
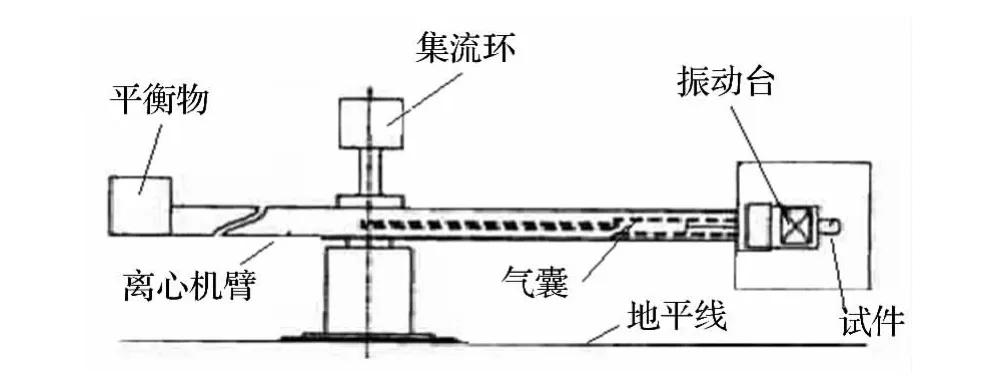
图1 离心-振动试验系统示意图Fig.1 Diagram of centrifuge force-vibration test system
整个离心-振动试验系统可简化为两个部分,电路部分和机械部分,如图2所示。
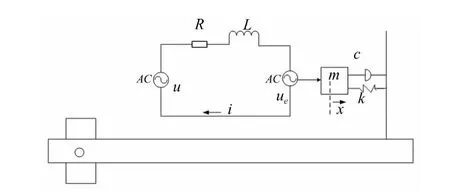
图2 离心力-振动试验系统物理模型Fig.2 Physics model of centrifuge force-vibration test system
为进一步简化系统模型,做以下三点假设:① 电动振动台只有一个自由度;② 气隙磁通密度为常数;③电动振动台等效为一个刚体。则振动台的动力学模型可表示为[17]:
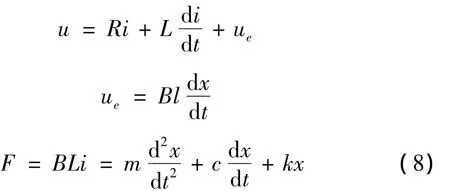
再根据多刚体动力学方程,在离心力作用下振动台面所受广义力为:

将以上离心-振动试验系统动力学模型描写成状态方程为:
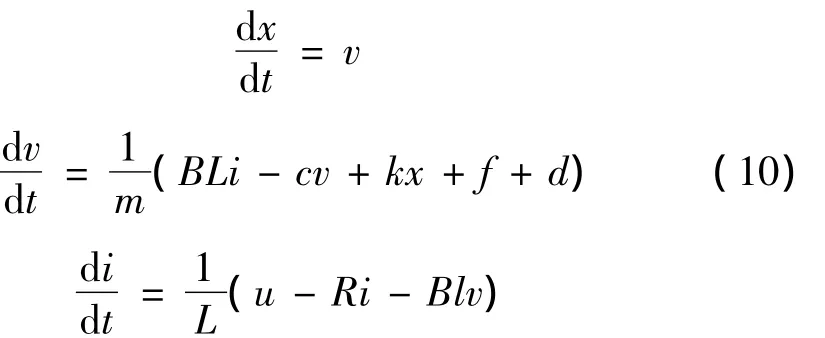
2.2 离心-振动试验系统振动位移跟踪高阶终端滑模控制器设计
设振动位移的给定值与实际值的误差为:e=xx*,设计如下的终端滑动模面为:
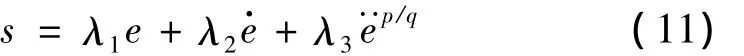
选择实常数λi(i=1,2,3)使系统具有期望的动态性能,其中,λi>0,1 < p/q<2,p,q均为正奇数。那么有如下定理:
定理1:对于式(10)和(11)构成的离心-振动试验系统,如果选择如下控制律:
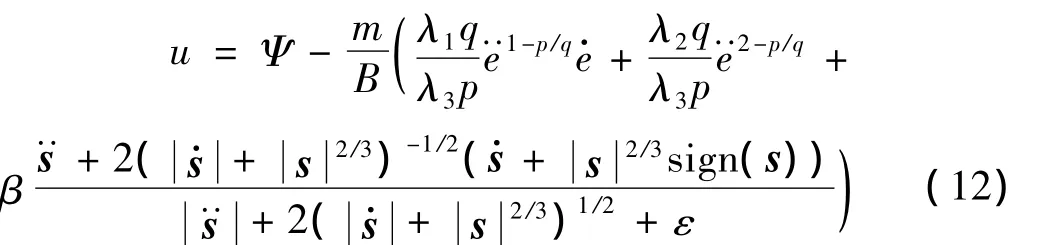
其中:β为设计参数,加入ε为保证控制输入更加光滑,Ψ的具体表达见证明过程。在该控制律作用下,能够使系统到达滑模面流形,并保证系统在有限时间内收敛。
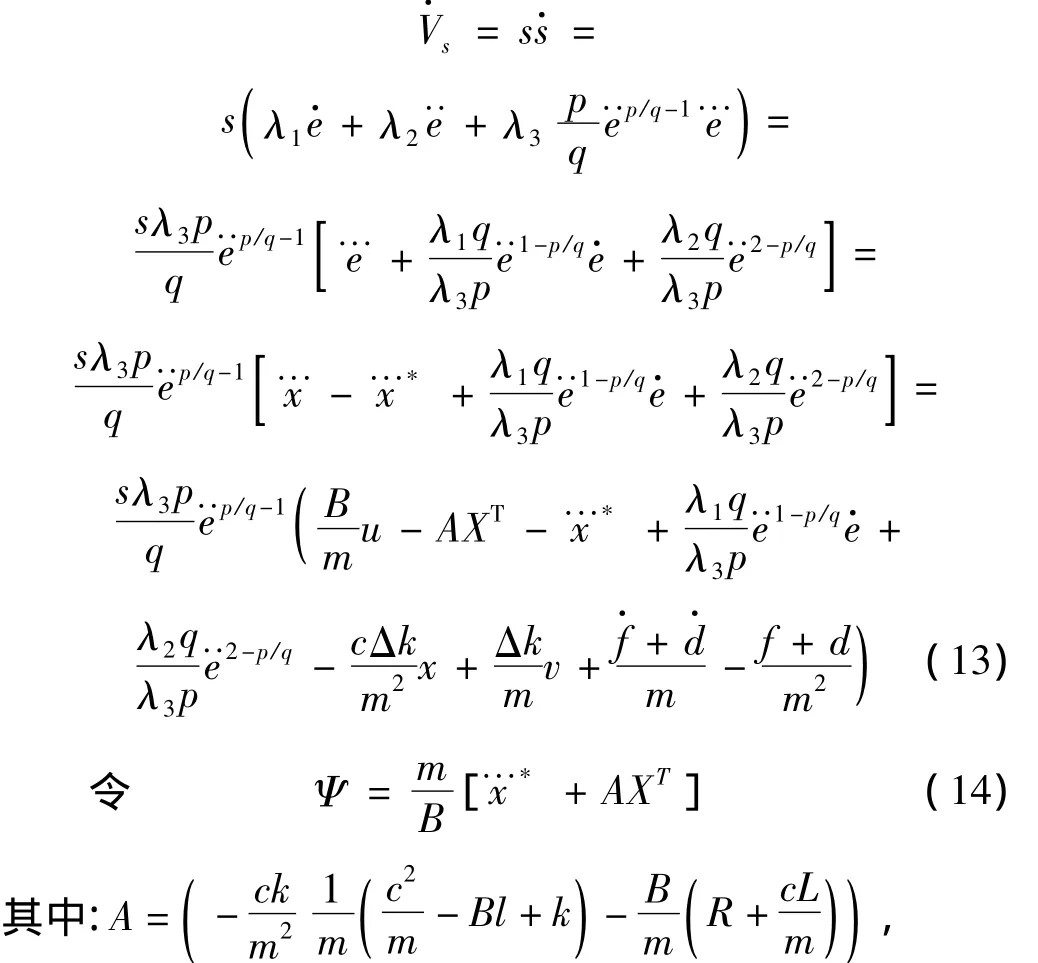
X=(x v i)为状态变量。
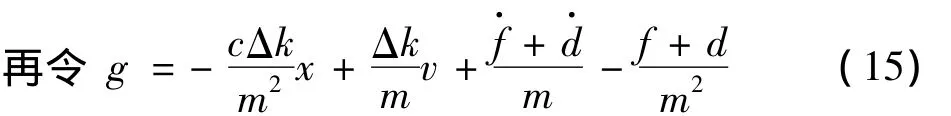
将控制律(12)代入上式(13),可得:
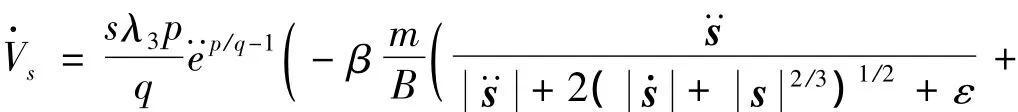

其中:α≥0,则上式满足的充分条件为:
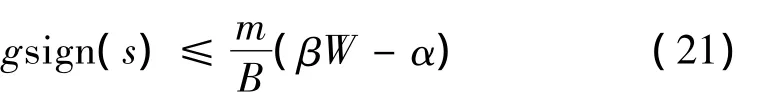
由式(18)可得:
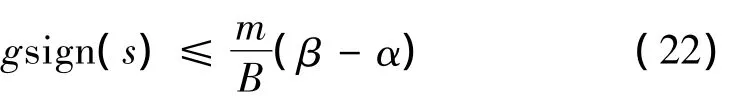
由于g的上界是已知,可通过系统的干扰和不确定性估计得到。从而只要满足:
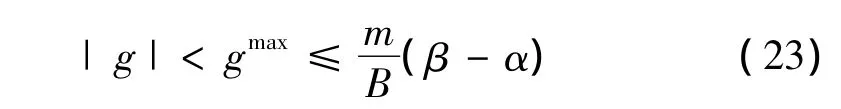
就有V<0,只要选择合适的β值,使上式成立,因此,根据李雅普诺夫稳定性理论知,系统将在有限时间到达并停留在终端滑模面s=0上。
当系统状态到达滑模面时,由(11)式s=0有:
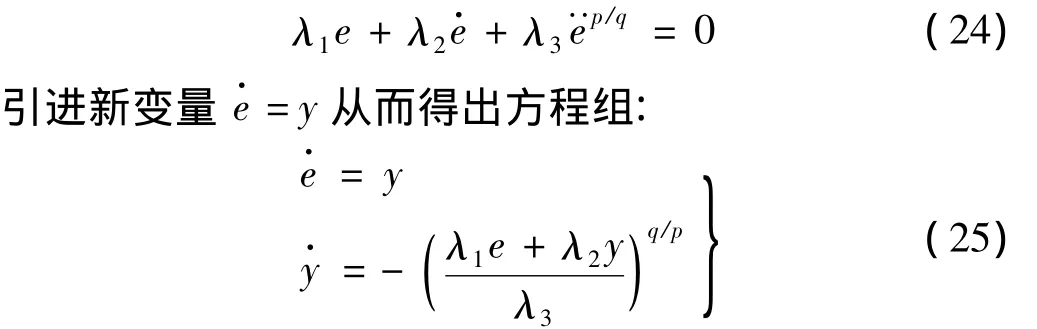
令方程组右端等于零,得到方程唯一解:

3 仿真结果及分析
为验证本文所提出的振动位移跟踪控制方法的可行性和有效性,选取如下离心振动复合系统参数进行数学仿真。台面、动圈等效质量m=1.5 kg;刚度k0=9 500 N/m;阻尼c=50 N/(m·s-1);磁感应强度B=0.5 T;动圈长度 l=28 m;电阻 R=0.5 Ω;磁感 L=100 μH;初始位移 x0=0,速度 v0=0,电流 i0=0;r=1.5 m;期望振动为正弦位移 x*=0.04sin(2πt/4)及阶跃输入;干扰力为 d=sin(2πt/16)×10-2。系统参数与控制器参数值分别取以下值:λ1=λ2=λ3=0.5;β =0.8;p=5,q=3,α =0.5;ε =0.005;ω = π/6 rad/s。仿真结果如图3~图6所示,分别给出了正弦振动位移跟踪曲线、方波响应曲线,控制输入曲线及误差曲线。
从图2、图3跟踪曲线可以看出,采用文章所用的算法的位移跟踪速度非常快,尤其对于方波输入响应,能够快速恢复到给定值,表明尽管系统存在较大的不确定性和干扰下,但由于采用了二阶终端滑模和准连续高阶滑模技术,有效消除了不确定性和外干扰的影响,使得输出振动位移能够比传统滑模更快的跟踪指令信号。从图4控制输入曲线可以看出尽管没有完全消除控制量的抖振现象,但已经大大地降低了抖振。图5误差曲线表明传统滑模由于没有采取去抖振措施使得控制精度相对较低。
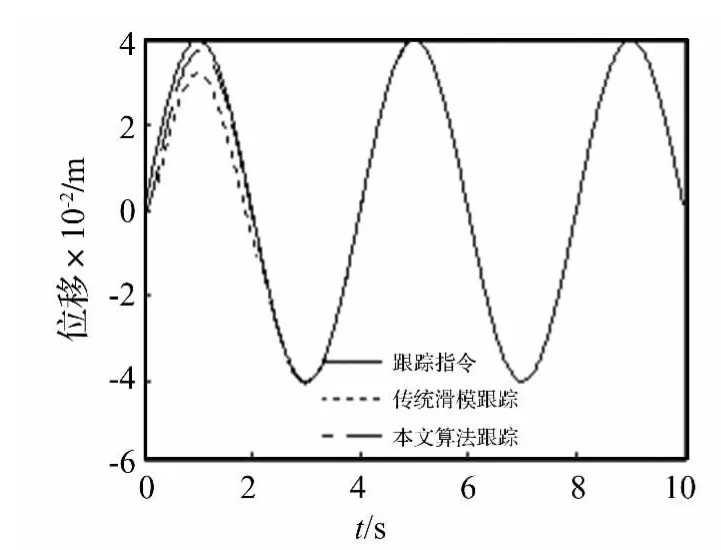
图3 正弦振动响应曲线Fig.3 Response curve of sines vibration
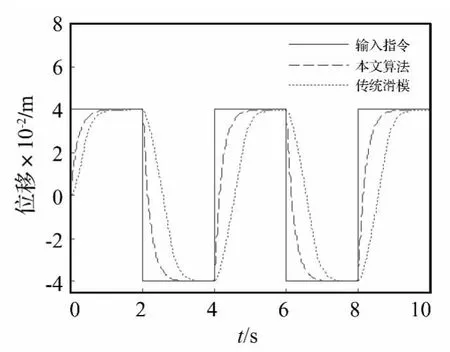
图4 方波响应曲线Fig.4 Response curve of square wave
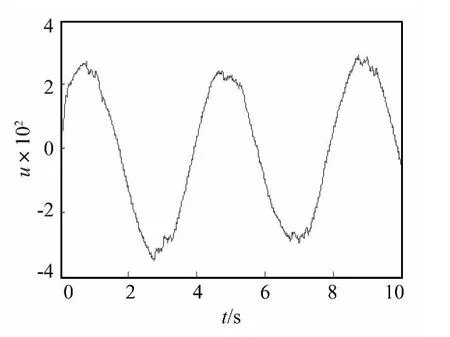
图5 正弦控制输入曲线Fig.5 Input curve of sine control
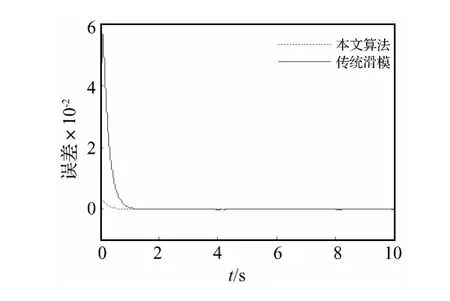
图6 振动位移跟踪误差曲线Fig.6 Error curve of displacement vibration
以上仿真的结果可以看出,准连续高阶终端滑模控制器能够在外界干扰和系统参数不确定情况下,使系统快速进入稳态,并完成离心振动复合系统振动位移跟踪控制,从验证了高阶终端滑模控制器的有效性和合理性。同时,高阶终端滑模控制器也有效的降低了抖振现象,系统本身控制量变得更加光滑,并显著地提高了跟踪速度。
4 结论
本文针对电动振动台在离心力作用下存在模型不确定性和外界干扰情况下的振动位移跟踪控制问题,通过高阶滑模控制理论,设计了基于高阶滑模的离心-振动复合系统的振动位移跟踪控制器。为了快速跟踪输入指令,根据建立的离心-振动复合系统的数学模型的特点,引入二阶终端滑模面,并通过李雅普诺夫第二法及反馈控制理论,建立了高阶终端滑模控制器,证明了其稳定性和全局收敛性。仿真结果表明,高阶终端滑模振动位移跟踪控制器能够有效消除滑模控制的“抖振”现象,与传统滑模控制相比能够快速地和精确地跟踪输入指令,进一步说明了该设计理论的正确性及方法的可行性。
[1]朱先辉,闰桂荣,牛宝良,等.离心力场中电动振动台的建模[J].振动与冲击,1999,18(3):37-44.ZHU Xian-hui, YAN Gui-rong, NIN Bao-liang, et al.Modelling of electrodynamic vibrator under centrifugal fore field[J].Journal of Vibration and Shock,1999,18(3):37 -44.
[2] Dupont P E.Avoiding Stick-slip Through PD Control[J].IEEE Transactions on Automatic Control,1994,39(5):1094-1097.
[3] Armstrong B,Neevel D,Kusik T.New results in NPID control:tracking,integral control,friction compensation and experimental results[J].IEEE Transactions on Control Systems Technology.2001,9(2):399-406.
[4]Karshenas A M,Dunnigan M W,Williams B W.Adaptive inverse control algorithm for shock testing[J].IEEE Proc-Control Theory and Applications,2000,147(3):267 -276.
[5] Groud D R,Gupta H O,Agarwal P.Design of random vibration controller using adaptive filtering[J].International Journal of Recent Trends in Engineering,2009,2(5):75-79.
[6]吴忠强,夏 青.基于奇异摄动理论的电液伺服系统Backstepping滑模自适应控制[J].振动与冲击,2012,31(11):154-157.WU Zhong-qiang,XIA Qing.Backstepping sliding mode adaptive control of an electro-hydraulic servo system based on singular perturbation theory[J].Journal of Vibration and Shock,2012,31(11):154-157.
[7]Man Z H,Palinski A P,Wu H R,et al.A robust MI-MO terminal sliding mode control for rigid robotic manipulators[J]. IEEE Transactions on Automatic Control,1994,39(12):2464-2468.
[8]Yu X H,Ma Z H.Fast terminal sliding mode control design for nonlinear dynamical systems[J].IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications,2002,49(2):261-263.
[9] Feng Y,Yu X,Man Z.Non-singular adaptive terminal sliding mode control of rigid manipulators[J].Automatica,2002,38(12):2159 -2167.
[10] Feng Y,Han X,Wang Y,et al,Second-order terminal sliding mode control of uncertain multivariable systems[J].International Journal of Control,2007,80(6):856 862.
[11] Feng Y,Yu X,Han F,On nonsingular terminal sliding mode control of nonlinear systems[J].Automatica,2013,49(6):
1715 1722.
[12] Levant A.Higher-order sliding modes,differentiation and output-feedback control[J].International J. of Control,2003,76(9/10):924-941.
[13] Levant A.Homogeneity approach to high-order sliding mode design[J].Automatica,2005,41:823 - 830.[14] Arie Levant.Quasi-continuous high-order sliding-mode Controllers[J].IEEE Trans on Automatic Control,2005,50(11):1812-1816.
[15]Pukdeboon C,Zinober A S,Thein M W.Quasi-continuous higher-order sliding mode controller designs for spacecraft attitude tracking maneuvers[J].IEEE Trans on Industrial electronics,2008,57(4):1436 -1444.
[16] Shtessel Y B,Christian H.Integrated higher-order sliding mode guidance and autopilot for dual-control missiles[J].J of Guidance,Control,and Dynamics,2009,32(1):79-94.
[17]郭继峰,任万滨,康云志,等.电动振动台模型辨识方法
及其应用的研究[J].振动与冲击,2011,30(7):241-244.
GUO Ji-feng,REN Wan-bin,KANG Yun-zhi,et al.Model identification method for a electrodynamic vibration shaker and its application[J].Journal of Vibration and Shock,2011,30(7):241-244.

