基于2.5维有限元-边界元分析轨道随机不平顺影响下的铁路地基振动
冯青松,雷晓燕
(华东交通大学“铁路环境振动与噪声”教育部工程研究中心,南昌 330013)
随着高速、重载铁路的快速发展,列车运行产生的环境振动污染对周围居民的日常生活和工作、精密仪器的生产和使用、古建筑的结构安全等产生日益严重的影响,受到人们的广泛关注。在铁路环境振动领域,列车运行引起的地基振动是最基本的问题之一,是进行环境振动预测评估、减振及隔振设计的基础。近年来围绕列车引起的地基振动问题,出现了许多有代表性的成果[1-24],当前国内外学者[1-12]一般采用基于频率-波数域的解析或半解析法,数值计算方法如有限元[13-20]、有限元 - 边界元混合法[21-24]等建立各种理论分析模型,以期在铁路线路设计阶段,对地基振动进行准确的预测分析。
解析或半解析模型[1-12]具有高效的计算效率,但由于采用了许多简化假定,使其适用范围、准确度受到很大的限制。在解析模型中,道砟和路基一般被简化为连续梁或连续的弹性质量块,但如何从实际工况中推算出合适的道砟、路基的参振质量和刚度至今还很难解决。地基一般简化为各层平行的无限大层状土体,而实际地基分布具有明显的不规则性,而且在地基隔振设计中,隔振沟、隔振墙等隔振屏障破坏了地基的连续性,这时解析模型很难适用。
地基振动数值计算模型通常采用3维有限元模型[13-15]或3 维有限元 -边界元模型[21],其具有强大的分析能力,能较好地适应复杂系统的不同状况。但由于铁路地基振动问题影响因素众多,特别是地基为无限大弹性体,当列车高速运行时,三维计算模型必须很大,计算时间步长需很短,这样计算成本很高。
在铁路地基振动分析中,铁路轨道、路基和地基可近似认为在轨道方向是均匀的,即沿轨道方向,结构的几何形状和材料性质不变。这时一种更有效的数值计算模型2.5维模型能获得较好应用。在2.5维模型中,沿无限长轨道方向传播的波可分解为一系列简谐波,每个简谐波对应一个确定的波数;在充分大的范围内选择足够多的波数值,对每一个简谐波,只需对轨道-路基-大地系统的横截面进行离散,计算得到该波数对应的响应;最后根据各波数下的响应,利用傅里叶逆变换得到实际的振动响应。与3维数值模型相比,由于2.5维数值模型仅仅在横截面上进行离散,其计算效率获得了极大提高。在线路设计阶段,需进行大量的方案比较,此时2.5维数值模型的优越性更能体现出来。当前一些学者已经采用2.5维有限元[16-20]或2.5维有限元 -边界元方法[22-24]研究地基振动。文献[16-20]采用2.5维有限元法分析了移动轴荷载或谐荷载作用下的地基振动,但未考虑车辆-轨道耦合振动的影响。文献[22-24]采用2.5维有限元-边界元研究大地振动,考虑了车辆-轨道耦合振动的影响,但轨道结构采用仅考虑垂向振动的解析平面层状梁模型。
本文采用2.5维有限元-边界元方法有效模拟了轨道-路基-地基系统的各个部分,结合解析模型和轨道不平顺功率谱密度,提出了地基振动功率谱的计算方法,与现场试验数据进行了对比验证了模型的合理性。
1 2.5维有限元-边界元模型
假定弹性体沿x方向无限长,各横截面(垂直于x轴的横截面,以下同)的几何和材料特性都是相同的。按同样的方式将三维弹性体各横截面划分为一系列平面单元,则x处和x+dx处横截面相对应的平面单元形成块体单元;按常规3维有限元方法可建立三维弹性体的动力微分方程;对此微分方程做x方向的傅里叶变换,并假定作用在弹性体上的结点力均为谐荷载,则在频率-波数域内三维弹性体的动力微分方程可表示为[25]:
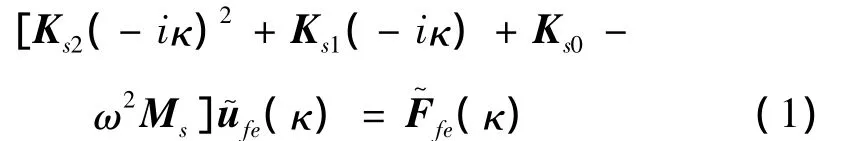
式中:Ks2、Ks1、Ks0为刚度矩阵,Ms为质量矩阵,分别为位移和结点力向量 κ为振动波数(rad/m)。结点力频率为Ω,沿x方向以速度c移动,结点力对应于波数κ的简谐分量的角频率为:

对每一个波数κ,方程(1)与坐标x无关,只与坐标y、z有关,这样只需对横截面进行有限元离散,横截面上的平面单元实际表示的是三维弹性体块体单元。
除块体单元外,当弹性体还采用梁单元模拟时,如铁路轨道结构中的钢轨,采用梁单元模拟更方便、合理,此时需考虑梁单元和块体单元的耦合。本文模型中梁单元不定义新的结点,梁单元沿x、y、z三个方向的平动位移和转角由块体单元上相邻两结点沿三个方向的平动位移线性插值求得。这样整个弹性体结构的动力微分方程式(1)可改写为:
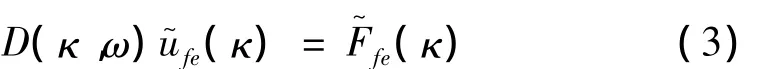
式中:
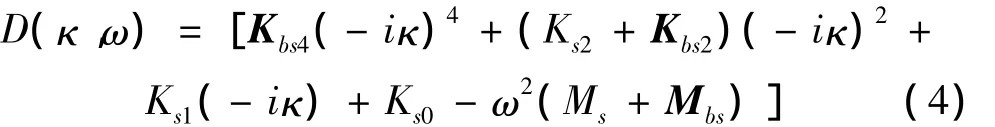
Kbs4、Kbs2为与梁单元相关的刚度矩阵,Mbs为与梁单元相关的质量矩阵,其具体表达式参见文献[25]。
具有有限横截面的轨道、路基等弹性体可采用2.5维有限元模拟,对于具有无限大横截面的地基等弹性体,采用边界元法模拟更合理。Sheng等[22]已根据积分互等定律推导出2.5维边界元法,边界单元采用形状函数为二次多项式的三结点单元。无限大弹性体的边界元基本方程为:
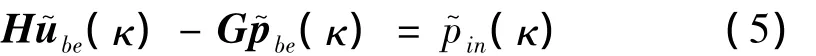
式中:u~be(κ)、p~be(κ)为边界单元结点的位移向量和面力向量,p~in(κ)为作用在边界上的面力、H、G为系数矩阵方阵。
除基本方程外,还需考虑边界条件。边界元法中的基本边界条件可表示为:

当弹性体采用有限元与边界元混合模拟时,在公共交界面(如路基底与地基表面)上有限元方程(3)必须与边界元方程相耦合。为便于建模求解,本文中有限元与边界元耦合交界面上的结点保持一致,且都具有二次多项式的形函数。在耦合交界面上有限元结点位移u~feⅡ(κ)等于边界元的结点位移 u~beⅡ(κ),即有:
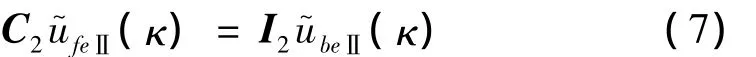
式中:C2、I2为单位矩阵。边界单元总结点包括有限元与边界元耦合界面上结点与非耦合界面上的结点,则边界单元总结点位移为
有限元区域与边界元区域耦合交界面上的相互作用力为面力。在边界元法中该面力为结点面力的函数,包含在式(5)的结点面力向量p~in(κ)中;而在有限元法中该相互作用面力表示为等效结点力,此时需将结点面力转换为等效结点力。根据虚功原理,在公共界面上任意有限单元的等效结点力所作的虚功等于相应边界元内结点面力所作的虚功,则将作用在有限元上的结点面力转换为等效结点力为:

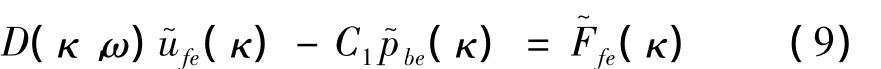
联立求解方程(5)、(6)、(7)和(9),则考虑有限元与边界元耦合时,系统结构的全局方程可表示为:
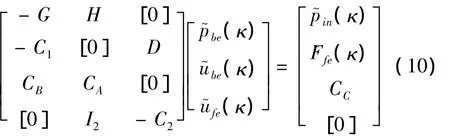
边界单元每个结点有三个位移分量和三个面力分量;在公共交界面上有限单元结点与边界单元的结点位置相同,每个有限单元结点也有三个位移分量;这样,边界单元的边界约束条件方程数(即式(6)和式(7)方程总数)刚好等于结点面力 p~be(κ)的阶数,全局方程(10)左边系数矩阵为一方阵;对每一个波数κ,求解线性方程组(10)则得边界单元所有结点的位移和面力分量、有限单元所有结点的位移分量。与常规有限元边界元耦合方法相比,本文将边界元的结点面力也看作一未知量,求解方程组时不需要将边界元方程(5)转换成类似有限元方程(3)的等效结点力-结点位移的形式。
利用此2.5维有限元-边界元模型可得到移动荷载作用下弹性体结构的振动响应。当轨道-路基-地基系统作为弹性体时,轨道-路基可采用有限元模拟,地基可采用边界元模拟,在路基底与地基表面交界面上有限元与边界元耦合,这样可求出移动谐荷载作用下轨道-路基-地基系统各部分的动力响应。
2 轨道随机不平顺影响下列车运行引起的地基振动功率谱求解
地基振动分析一般考虑两种主要列车荷载激励:移动轴荷载、轨道随机高低不平顺引起的垂向动态轮轨力,且后者的影响一般更显著[5]。为了与实际测试结果相比较,需探讨两种主要激励影响下地基振动功率谱求解方法。文献[1]建立了解析的车辆-轨道-地基耦合模型,并提出了一种轨道随机不平顺影响下地基振动功率谱的计算方法。本文参考文献[1]方法,联合运用2.5维有限元-边界元模型和解析模型,建立地基振动功率谱的求解方法。
地基上点(x,y,z)处频率为f的垂向位移功率谱可表示为[1]:
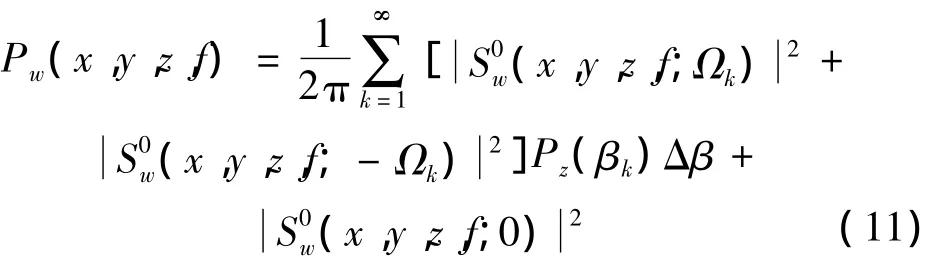
式中:Pw(x,y,z,f)为垂向位移功率谱(m2/Hz2);S0w(x,y,z,f;Ωk)为单位幅值的轨道高低不平顺引起的垂向位移频谱(1/Hz);该不平顺可表示为 z (x)=eiβkx,βk为轨道不平顺的波数(rad/m),βk=2π/λ,λ为不平顺的波长,此时车辆以频率Ωk=βkc振动,轨道不平顺引起的第l个垂向动态轮轨力为Pl(t)=P~l(Ωk)eiΩkt,其中 l =1,2,…,M,M 为 轮载总数;S0w(x,y,z,f;0)为移动轴荷载引起的垂向位移频谱,即Ωk=0;Pz(βk)为轨道高低不平顺功率谱密度(m3/cycle);Δβ为轨道不平顺的波数间隔(rad/m)。
由式(11)可知,位移功率谱的计算主要是位移频谱幅值 S0w(x,y,z,f;Ωk)的计算。由文献[2]知,
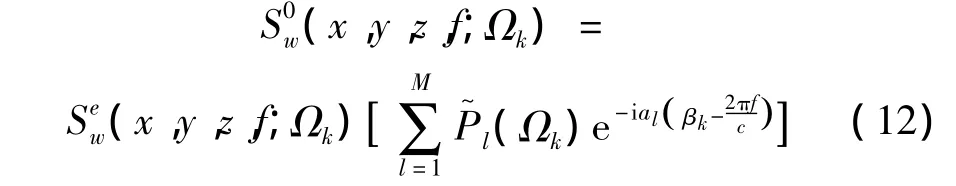
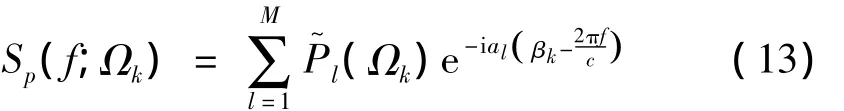
为垂向轮载谱,其表示单位幅值的谐波高低不平顺影响下,列车一系列轮对通过时垂向总轮载的谐荷载部分;al为t=0时第l个轮载距原点的距离。由文献[3]知,移动的单位垂向谐荷载作用下地基表面振动位移频谱可表示为:
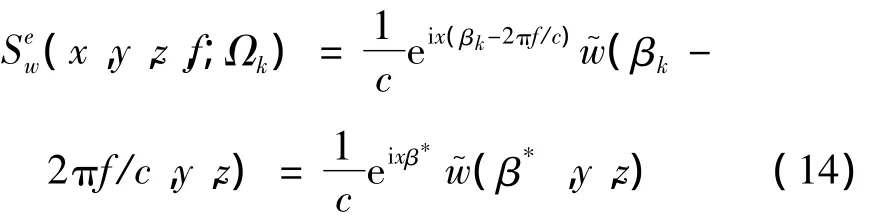
联立式(12)、(13)和(14),且只考虑幅值有:

将式(15)代入式(11),得:
垂向轮载谱幅值 Sp(f;Ωk)可利用作者已建立的车辆-轨道-路基-地基耦合系统垂向振动解析模型[11]得到;傅里叶变换域内垂向位移幅值 w~(βk,y,z )可利用本文建立的2.5维有限元-边界元模型得到;利用2.5维有限元-边界元模型计算结果和解析模型计算结果,由式(16)可得地基振动的垂向位移功率谱。地基振动速度功率谱P·w(x,y,z,f)和振动加速度功率谱P·w·(x,y,z,f)可表示为:
式(16)、(17)和(18)除以列车通过观测点的时间,可得到相应的振动响应功率谱密度估计值。
3 计算模型的验证
为了验证计算模型的合理性,选取一地基振动典型实例比较分析模型计算结果与现场测试结果。典型实例选取文献[4]在意大利Via Tedalda地点的测试,该测试工况中列车、轨道、路基与地基详细参数已在文献[4,23]中给出。
根据测试工况下轨道-路基-地基系统,建立相应的2.5维有限元-边界元模型,见图1。具有有限横截面尺寸的有砟轨道-路基采用2.5维有限元模拟,无限大的层状地基采用2.5维边界元模拟,在路基底面考虑有限元与边界元的耦合。
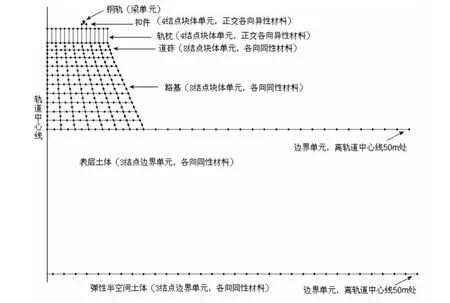
图1 2.5维有限元-边界元模型Fig.1 2.5 - Dimensional finite element-boundary element model
UIC60钢轨被模拟为梁单元,考虑沿x轴(沿轨道中心线方向)的纵向运动、在y轴方向(垂直于轨道中心线的横向)、z轴方向(竖直方向)的弯曲、绕x轴的转动。每根钢轨在y轴和z轴方向的弯曲刚度为1.08×106Nm2、6.4×106Nm2;扭转刚度和转动惯量假定为合理的值1.0 ×1010Nm2、100 kgm;钢轨质量60 kg/m。离散支承的钢轨扣件(包括垫板影响,以下同)、轨枕被等效为连续支承结构,采用4结点块体单元模拟。由于扣件和轨枕的离散支承特性,故实际扣件与轨枕中沿x方向的剪切波是不存在的,为真实模拟这种现象,模型中扣件和轨枕采用正交各向异性材料,沿x方向的弹性模量和与x方向有关的剪切模量都取为零。扣件在垂直方向的弹性模量为N/m2为每个扣件在垂直方向的刚度,brp和hrp为块体单元的宽和高,d=0.6 m为轨枕间距,当块体单元宽和高相等时,即 brp=hrp,则 Ez,rp=krp/d;扣件的损失因子 ηrp取0.15。本文只关心垂向振动,扣件的剪切模量、除垂向的其它方向的弹性模量都取为零;扣件质量很小忽略不计。每根混凝土轨枕长lsl为2.5m,轨枕截面的平均宽度和高度分别为 bsl=0.25 m、hsl=0.2 m,轨枕质量 msl为294 kg;轨枕的弹性模量Esl和泊松比vsl分别取3.0×1010N/m2和0.15。采用4结点块体单元划分轨枕,块体单元横截面取实际轨枕尺寸lsl×hsl,在y和z方向上的等效弹性模量为 E—y,sl=E—z,sl=Esl× bsl/d,此时连续的轨枕块体单元的弯曲刚度与实际的轨枕弯曲刚度等效;在y-z平面内的等效剪切模量为=msl/(d×lsl×hsl)。采用具有各向同性材料特性的8结点块体单元模拟连续的道砟和路基结构。道砟表面宽2.5 m,底宽 2.7 m,厚度为 0.3 m;道砟弹性模量 Eb=36.35 ×106N/m2,密度 ρb=1 538.5 kg/m3,泊松比 vb=0.33,损失因子取1.0。路基表面宽2.7 m,底宽 4 m,厚1.5 m;其密度、弹性模量、损失因子和泊松比分别为1 800 kg/m3,20 MN/m2,0.05 和 0.45。地基结构考虑为弹性半空间体上覆盖10 m厚的一层土;两层土体密度都取1 800 kg/m3,损失因子取0.1;表层土体的P波和S波速度为995 m/s和300 m/s;弹性半空间土体的P波和S波速度为1 990 m/s和600 m/s。
整个2.5维有限元-边界元模型中,钢轨、扣件、轨枕、道砟、路基共划分为170个有限单元;地基由边界元模拟,采用最大单元长度为0.5 m的3结点边界单元对地基表面边界和分层土体交界面边界进行离散,边界截断设在距轨道中心线50 m处,且在边界单元末端设置一特殊的边界单元[22],以消除波反射的影响。有限元与边界元的单元尺寸,直接影响弹性体中波传播特性的模拟精度,单元划分主要与单元类型、弹性体内传播的剪切波波长(取决于波速和频率)等因素有关。在本文考虑的100 Hz分析频率范围内,上述有限元与边界元的单元划分可保证地基振动响应的计算精度。
正如在章节 2中所述,垂向轮载谱幅值
Sp(f;Ωk)由作者已建立的车辆-轨道-路基-地基耦合系统垂向振动解析模型[11]得到。在解析模型中,轨道-路基被模拟为平面的层状梁模型;车辆考虑为运行于轨道上的多刚体系统,单节车辆采用整车附有二系弹簧质量车体模型,地基考虑为三维的层状弹性体。在文献[1,11,26]已证明,利用该解析模型,可有效保证轨道谐波高低不平顺引起的垂向动态轮轨力计算的可靠性。本文考虑5节ETR500客运列车,列车速度25 m/s(90 km/h)。参考文献[4,27],确定车辆模型基本参数,见表1。根据2.5维有限元-边界元模型中的轨道、路基参数,推导出解析模型中轨道-路基系统平面层状梁模型参数,见表2;地基土层参数与2.5维有限元-边界元模型中的相同。利用解析模型可得到不同波长的单位幅值高低不平顺引起的垂向动态轮轨力幅值 P~l(Ωk),继而得到垂向轮载谱幅值 Sp(f;Ωk)。
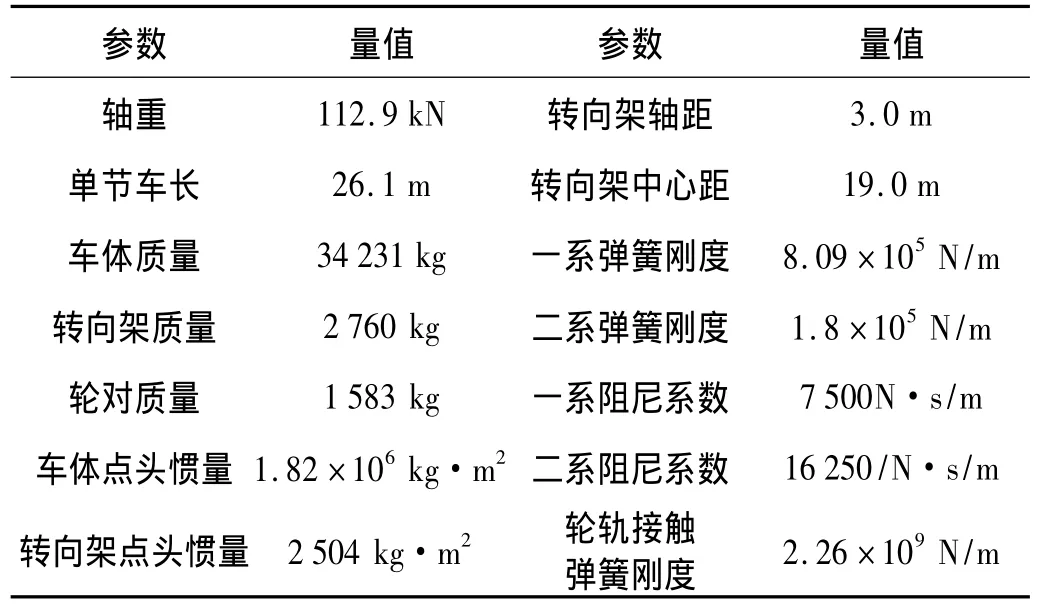
表1 ETR500车辆基本参数Tab.1 Basic parameters of the ETR500 vehicle

表2 轨道-路基系统基本参数Tab.2 Basic parameters of the track-embankment system
选取典型的轨道随机高低不平顺单边功率谱密度Pz(βk),见图2;该功率谱密度结合了轨检车测量的长波数据和典型功率谱密度得到的短波数据。
文献[4]中在意大利Via Tedalda地点测试了距轨道中心线13 m和26 m两个测点的地基表面振动。利用本文模型预测的两个测点垂向加速度振级与实测值的比较结果见图3和图4,加速度振级参考值取1×10-6m/s2。由图可看出:理论计算的1/3倍频程垂向振动加速度频谱与实测结果吻合较好,这证明了本文理论模型的合理性。在文献[4,23]中也对该测点进行了预测分析,与这两个文献相比,本文计算结果与实测结果的吻合性更好。
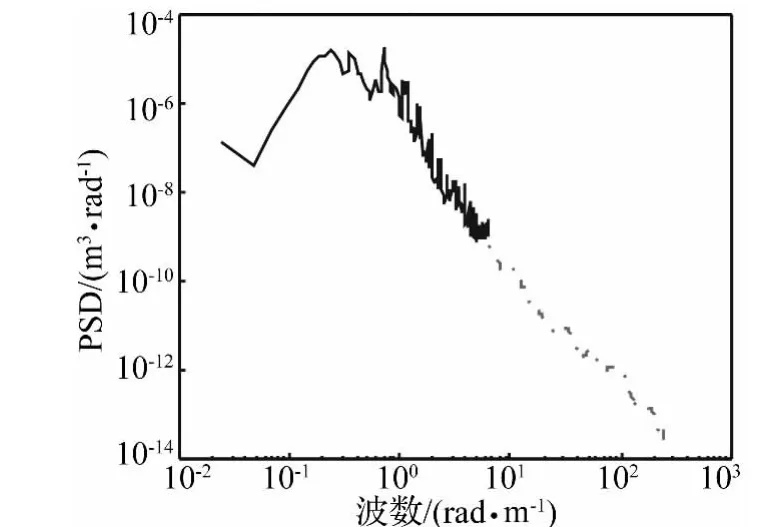
图2 轨道高低不平顺单边功率谱密度Fig.2 One-sided PSD of the vertical irregularities of track
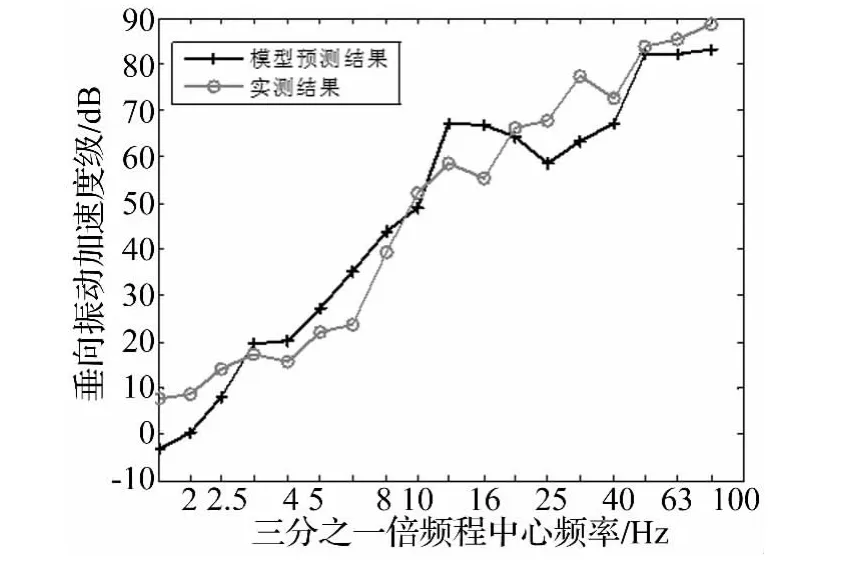
图3 距轨道中心线13 m测点的垂向振动加速度级Fig.3 Vertical acceleration level at 13 m from the track centre-line
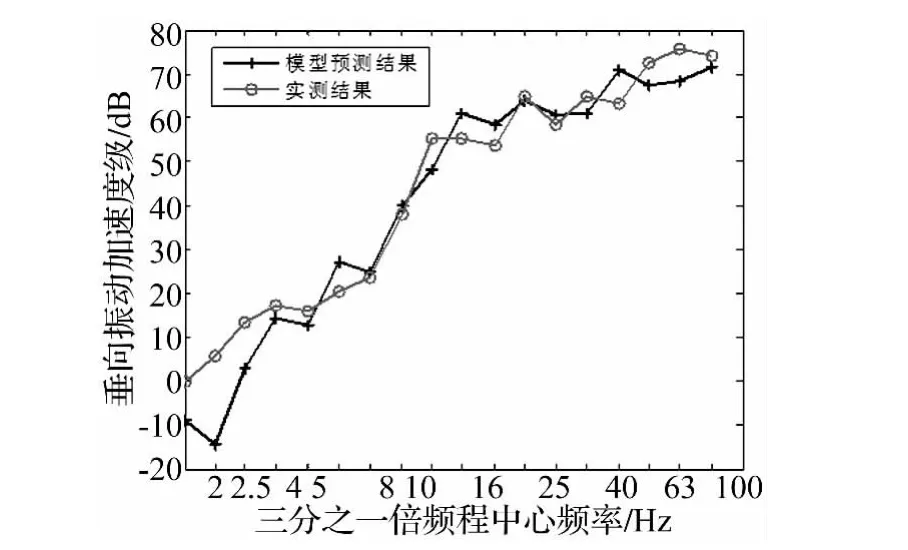
图4 距轨道中心线26 m测点的垂向振动加速度级Fig.4 Vertical acceleration level at 26 m from the track centre-line
4 结论
本文建立了完善的2.5维有限元-边界元耦合模型,能较好地计算移动谐荷载作用下钢轨、扣件、轨枕、道砟、路基和地基等各部分的振动响应;利用既有的车辆-轨道-路基-地基耦合系统垂向振动解析模型得到轨道谐波高低不平顺引起的垂向动态轮轨力;在2.5维有限元-边界元模型和解析模型的基础上,结合轨道随机不平顺功率谱密度,提出了轨道随机不平顺影响下列车运行引起的地基振动功率谱的计算方法。针对一地基振动实例,利用本文理论模型计算得到地基表面垂向振动加速度级,并与现场实测结果进行了对比分析,证明了本文所提模型的合理性。
本文所建模型能有效地分析具有复杂横截面形状的轨道-路基-地基系统的振动响应,能分析多种轨道、地基内减振隔振措施(如隔振沟、隔振墙、波阻块等)的影响,非常适合在铁路线路设计阶段的方案比较研究。
[1]Sheng X,Jones C J C,Thompson D J.A theoretical model for ground vibration from trains generated by vertical track irregularities[J].Journal of Sound and Vibration,2004,272:937-965.
[2] Sheng X,Jones CJC,Thompson D J.A theoretical study on the influence of the track on train-induced ground vibration[J].Journal of Sound and Vibration,2004,272:909 -936.
[3]Sheng X,Jones C J C,Petyt M.Ground vibration generated by a load moving along a railway track[J].Journal of Sound and Vibration,1999,228:129 156.
[4] Lai C G,Callerio A,Faccioli E,et al.Mathematical modeling of railway-induced ground vibrations[C]//Chouw N,Schmid G.Proceedings of the International Workshop Wave 2000.Germany:Taylor& Francis,2000:99-110.
[5] Lombaert G,Degrande G.Ground-borne vibration due to static and dynamic axle loads of intercity and high-speed trains[J].Journal of Sound and Vibration,2009,319:1036 -1066.
[6]边学成,陈云敏.列车荷载作用下轨道和地基的动响应分析[J].力学学报,2005,37(4):477 -484.BIAN Xue-cheng,CHEN Yun-min.Dynamic analysis of track and ground coupled system with high-speed train loads[J].Chinese Journal of Theoretical and Applied Mechanics,2005,37(4):477-484.
[7]谢伟平,胡建武,徐 劲.高速移动荷载作用下的轨道-地基系统的动力响应[J].岩石力学与工程学报,2002,21(7):1075-1078.XIE Wei-ping,HU Jian-wu,XU Jin.Dynamic response of track-ground systems under high speed moving load[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(7):1075-1078.
[8]李志毅,高广运,冯世进,等.高速列车运行引起的地表振动分析[J].同济大学学报(自然科学版),2007,35(7):909-914.LI Zhi-yi,GAO Guang-yun,FENG Shi-jin,et al.Analysis of ground vibration induced by high-speed train[J].Journal of Tongji University(Natural Science),2007,35(7):909-914.
[9]和振兴,翟婉明.高速列车作用下板式轨道引起的地面振动[J].中国铁道科学,2007,28(2):7 -11.HE Zhen-xing,ZHAI Wan-ming.Ground vibration generated by high-speed trains along slab tracks[J].China Railway Science,2007,28(2):7 -11.
[10] Xia H,Cao Y M,Roeck G De.Theoretical modeling and characteristic analysis of moving-train induced ground vibrations[J].Journal of Sound and Vibration,2010,329:819-832.
[11]冯青松,雷晓燕,练松良.高速铁路路基-地基系统振动响应分析[J].铁道科学与工程学报,2010,7(1):1 -6.FENG Qing-song,LEI Xiao-yan,LIAN Song-liang.Vibration analysis of high-speed railway subgrade-ground system [J].Journal of Railway Science and Engineering,2010,7(1):1 -6.
[12]蔡袁强,王 玉,曹志刚,等.列车运行时由轨道不平顺引起的地基振动研究[J].岩土力学,2012,33(2):327-335.CAI Yuan-qiang,WANG Yu,CAO Zhi-gang,et al.Study of ground vibration from trains caused by track irregularities[J].Rock and Soil Mechanics,2012,33(2):327 -335.
[13]Ju S H,Liao J R,Ye Y L.Behavior of ground vibrations induced by trains moving on embankments with rail roughness[J].Soil Dynamics and Earthquake Engineering,2010,30:1237-1249.
[14] Galvín P,Romero A,Domínguez J.Fully three-dimensional analysis of high-speed train-track-soil-structure dynamic interaction[J].Journal of Sound and Vibration,2010,329:5147-5163.
[15]和振兴,翟婉明,杨吉忠,等.铁路交通地面振动的列车-轨道-地基耦合数值方法研究[J].振动工程学报,2008,21(5):488 -492.HE Zhen-xing,ZHAI Wan-ming,YANG Ji-zhong,et al.Train-track-ground coupling numerical method for railway traffic induced ground vibration[J].Journal of Vibration Engineering,2008,21(5):488 -492.
[16]高广运,何俊锋,杨成斌,等.2.5维有限元分析饱和地基列车运行引起的地面振动[J].岩土工程学报,2011,33(2):234-241.GAO Guang-yun,HE Jun-feng,YANG Cheng-bin,et al.Ground vibration induced by trains moving on saturated ground using2.5D FEM[J].Chinese Journal of Geotechnical Engineering,2011,33(2):234-241.
[17]谢伟平,兰 洋.2.5维有限元法分析地铁列车引起的地基振动[J].武汉理工大学学报,2009,31(13):78 -82.XIE Wei-ping,LAN Yang.Ground vibration induced by subway train load using 2.5D finite element method [J].Journal of Wuhan University of Technology,2009,31(13):78-82.
[18]边学成,陈云敏.基于2.5维有限元方法分析列车荷载产生的地基波动[J].岩石力学与工程学报,2006,25(11):2235-2342.BIAN Xue-cheng, CHEN Yun-min. Ground vibration generated by train moving loading using 2.5D finite element method[J]. Chinese Journal of Rock Mechanics and Engineering,2006,25(11):2235 -2342.
[19] Yang Y B,Hung H H,Chang D W.Train-induced wave propagation in multi-layered soils using finite/infinite element simulation[J].Soil Dynamic Earthquake Engineering,2003,23(4):263-278.
[20] Gao G Y,Chen Q S,He J F,et al.Investigation of ground vibration due to trains moving on saturated multi-layered ground by 2.5D finite element method[J].Soil Dynamics and Earthquake Engineering,2012,40:87 -98.
[21] Auersch L.The excitation of ground vibration by rail traffic:theory of vehicle track soil interaction and measurements on high-speed lines[J].Journal of Sound and Vibration,2005,284:103-132.
[22] Sheng X,Jones C J C,Thompson D J.Modelling ground vibration from railways using wavenumber finite- and boundary-element methods[J].Proceedings of the Royal Society A,2005,461:2043-2070.
[23] Sheng X,Jones C J C,Thompson D J.Prediction of ground vibration from trains using the wavenumber finite and boundary element methods[J]. Journal of Sound and Vibration,2006,293:575-586.
[24] Galv n P,Francois S,Schevenels M,et al.A 2.5D coupled FE-BE model for the prediction of railway induced vibrations[J].Soil Dynamics and Earthquake Engineering,2010,30:1500-1512.
[25] Nilsson C M,Jones C J C.Theory manual for WANDS2.1 wave-number-domain FE-BE software for structures and fluids[R].ISVR Technical Memorandum No 975,Southampton:Southampton University ,2007.
[26]冯青松,雷晓燕,练松良.不平顺条件下高速铁路轨道振动的解析研究[J].振动工程学报,2008,21(6):559 -564.FENG Qing-song,LEI Xiao-yan,LIAN Song-liang.Vibration analysis of high-speed railway tracks with geometric irregularities[J].Journal of Vibration Engineering,2008,21(6):559-564.
[27] Liu K,Reynders E,Roeck G De,et al.Experimental and numerical analysis of a composite bridge for high-speed trains[J].Journal of Sound and Vibration,2009,320:201-220.

