基于同步压缩变换和局部替代数据的非平稳振动信号分解方法
胡异丁,任伟新,杨 栋,4
振动工程不可避免地涉及到响应信号的处理,通常假定信号是平稳的。然而,结构的时变和非线性以及外界激励的非平稳特征都有可能使得响应信号呈现出非平稳性。响应中可能包含了激励的某些非平稳特征和结构的某些固有特征,从而信号从整体看呈现非平稳性,但其中仍可能包含平稳成分信息[1]。因此数据的平稳性检验尤为必要。此外,找到方法从响应信号中分解出平稳成分和非平稳成分,则可为结构系统辨识更为细致的分类提供一种可能。
Xiao 和 Borgnat等[2-5]建立了在工作(Operational)意义下平稳性的研究理论框架,指出所谓平稳性应该相对于一定的持续时间内,及给定的观测尺度而言的,且可以由时频谱是否存在进化(Evolutionary)特性来决定,其概念的适用范围包括随机信号以及确定性的信号。换句话说,若在所有不同时间间隔内的局部的频谱统计特性与整个观测尺度内的全局频谱特性基本一致,则可认为平稳。基于这样的理解,利用替代数据(Surrogate)和多窗谱时频分析,比较信号全局和局部频谱特征来评价信号平稳性,并采用了零假设检验判定信号的平稳性。
小波变换由于其可变窗口,使其在低频部分获得较高的频率分辨率和较低的时间分辨率,而在高频部分获得较高的时间分辨率和较低的频率分辨率[6]。McCullough等[7]采用小波时间-尺度平面和替代数据评价信号的平稳性,并且提供了一种称为局部替代数据(Local Surrogate)的方法,在时频谱上非平稳信息存在的时间和频率位置反映出来。由于小波在时频上仍然比较模糊,降低了时频可读性。最近,Daubechies等[8-9]提出了一种基于小波变换的同步压缩变换方法,该方法在小波尺度方向上利用一种特别的重分配方法,将时间-尺度平面转化为时间-频率平面,同时提高时频聚集性,消除干扰项,从而进一步能洞察非平稳信号内部组成成分。
本文基于同步压缩变换和替代数据法实现了信号平稳性的检测,并且结合局部替代数据法提出了一种信号的平稳成分和非平稳成分分解的方法。数值算例说明该方法的有效性。
1 同步压缩变换
高质量的时频表示对于信号的可靠分析至关重要。信号可以看作由多个调制(调幅和调频)分量的叠加,小波变换作为一种时频工具广泛应用于提取脊线来获得这些分量的瞬时特征(如振动频率)。然而小波变换仍然比较模糊,降低了脊线的可读性。Daubechies提出的同步压缩变换大大增强了时频分辨率,使得在时频谱上获取脊线及其分量成为了可能。
信号的同步压缩变换是以小波变换为基础。首先给定小波母函数ψ(t),对信号x(t)进行连续小波变换(CWT):
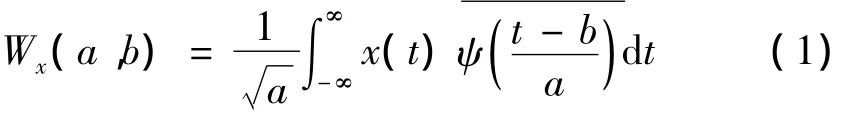
其中:a为尺度因子,b为平移因子,ψ(t )为 ψ (t)的共轭。
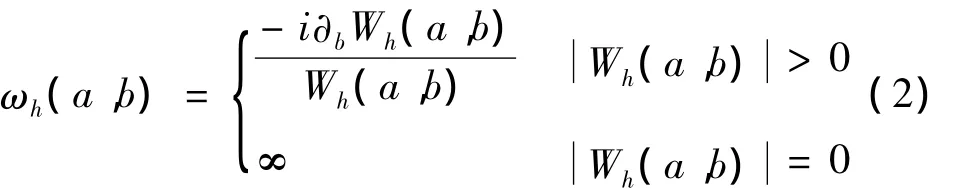
对任意信号x(t),在不至于混淆的情况下记ωx(a,b)为 ω(a,b),这样建立了(a,b)→(ω(a,b),b)的映射关系,同步压缩变换再对时间-尺度平面的能量进行重分配将其转化为时间-频率平面,其离散计算式为:
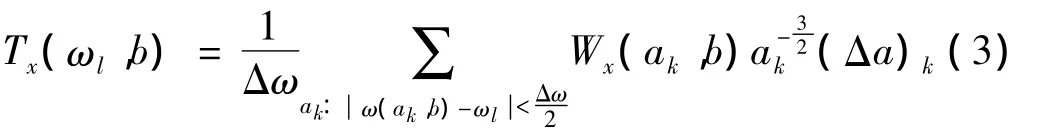
其中:ωl为第l个离散的角频率,ak为第k个离散的尺度点,Δω = ωl- ωl-1,(Δak)=ak- ak-1。最后瞬时频率可由f=ω/2π得到。
同步压缩变换是可逆的,对于离散计算,可以通过式(4)重构原始信号:
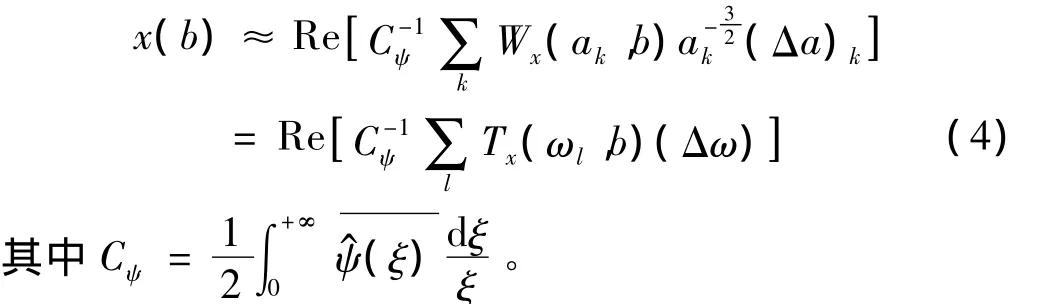
Thakur等[10]利用同步压缩变换的时频谱提取了脊线,成功分解了多分量非平稳信号,并应用于分析古气候学数据,证明了同步压缩变换为时频分析的有力工具,并提供了MATLAB工具箱[11]。
2 信号平稳性检测——时频替代数据法
轮次检验和逆排序检验是时间序列平稳性的检验常用的方法[12],但是对于具有时变频率的非平稳信号效果往往不佳[13]。信号平稳性利用替代数据法在可以在时频上来检验,其基本思想是对于给定的观测数据样本,在时频谱上比较该观测数据的全局谱和局部谱特征,若频谱特征选在整个观测时间内有较大变化,表明信号具有非平稳性,反之则是平稳的[5]。
替代数据最初是用于检验时间序列非线性的一种检验统计学方法[14]。根据Wiener-Khintchin定理,平稳随机过程的功率谱密度就是信号自相关函数的傅里叶变换[12]。由于研究对象是过程的一个观测样本,功率谱可看作该样本的傅里叶变换模平方除以观测时间长度。设观测数据x(t)的傅里叶变换为:
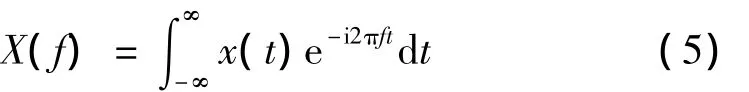
保持其傅里叶变换的幅度谱不变,而相位谱φf变为均匀分布在[-π,π]的随机相位。利用傅里叶反变换可以得到时域的替代数据,即:

由于替代数据的相位谱是均匀分布在[-π,π]的随机相位,通过这种方法产生的替代数据,具备原数据相同的功率谱幅度以及一阶矩二阶矩的统计特性,是广义平稳的[3]。
给定观测信号x(n),通过上述方法产生一组替代数据xj'(n)(j=1~J),对每个替代数据进行时频变换得到TFj(f,i)(j=1~J),其中 f 为频率,i为时间。替代数据的全局谱分布可通过其时频谱边际化来获得,局部谱为时频谱上某个时刻的频率分布。选择合适的距离测度来描述和全局谱分布和某个时刻局部谱分布的差别。则对于第j个替代数据,局部谱和全局谱的距离随时间变化的波动可用其经验方差来描述:
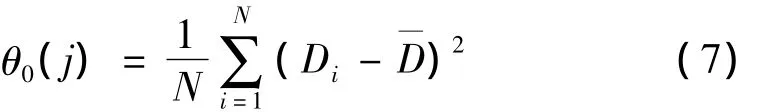
其中:Di为全局谱和第i个时刻局部谱的距离,为所有时刻该距离测度的均值,N为时间点数,θ0(j)表示第j个替代数据的距离分布的方差。
同样可求出原数据局部谱和全局谱的距离随时间变化的波动方差θ1:

利用伽马分布拟合θ0(j),置信度设为95%,即可确定阈值γ,从而实现平稳性的零假设检验:
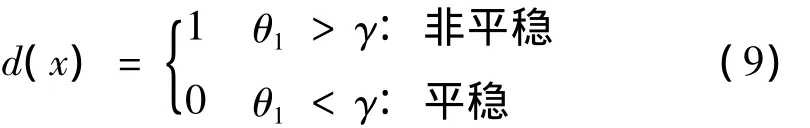
设平稳性零假设被拒绝,可定义平稳度指标为:
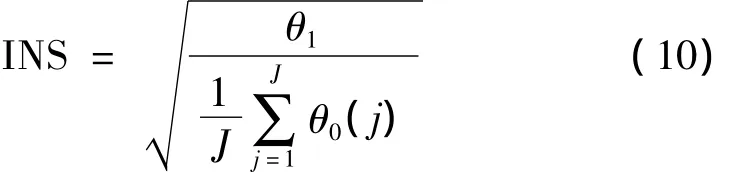
若信号是平稳的,则INS值在1附近,信号不平稳程度越大,INS的值也越大。
在同步压缩时频上应用替代数据法检测数据平稳性。选择欧氏距离作为评价局部谱分布和全局谱分布的距离测度。分析数据为汶川地震波,幅度缩小了100倍,采样频率为50 Hz,分析时长100 s。生成替代数据J=50次。分析结果如图1所示。其中(a)为原始数据和一个替代数据,(b)为原始数据和替代数据经同步压缩变换的时频图。(c)为检测结果,图中垂直虚线表示阈值 γ,垂直实线为 θ1,θ1>γ表明 θ1落在 θ0为平稳的概率密度区域之外,因此为检测结果等于1,为非平稳,非平稳指标INS=1.333 9。
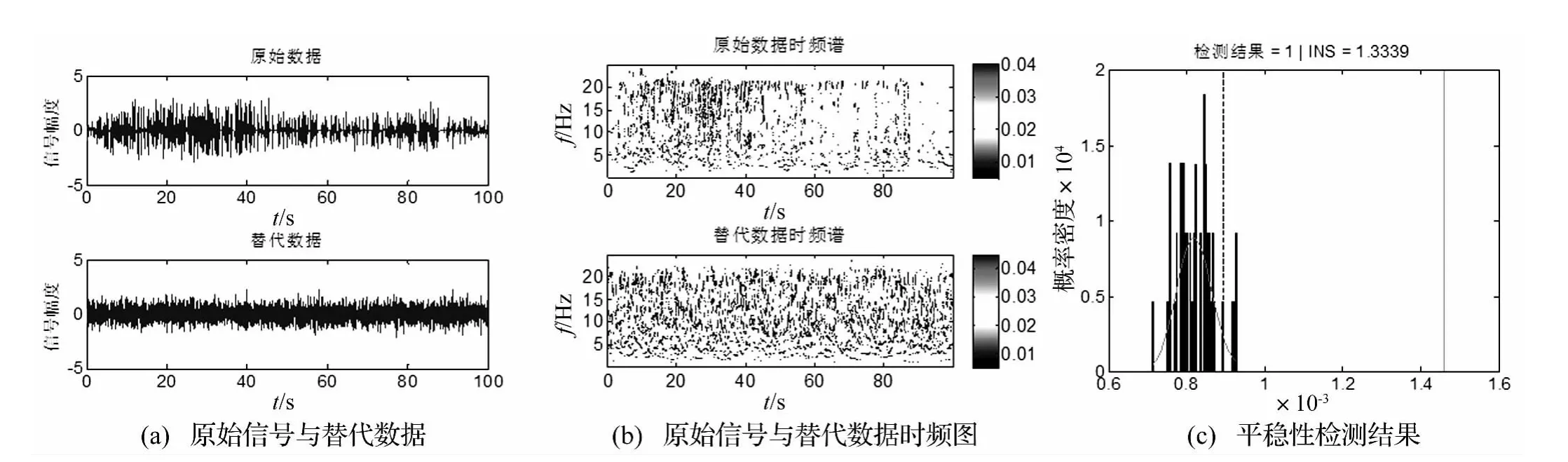
图1 同步压缩时频替代数据平稳性检测Fig.1 Stationarity test with synchrosqueezing transformation and surrogate
3 局部替代数据
McCullough等[7]采用小波时频和替代数据评价信号的平稳性,并且提供了一种称为局部替代数据的方法。首先对一非平稳信号x(t)生成一批替代数据,并分别做小波变换得到其小波系数,由于替代数据是平稳的,因此不包含原信号中有意义的非平稳信息,但是可能包含了由噪声引起的非平稳。对这些小波系数做平均:

其中:N为生成的替代数据的个数,Wi(a,b)为第i个替代数据的小波系数。在每个尺度及时间位置的标准差为:

设定阈值
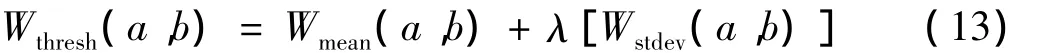
其中λ为一调整参数,可依据噪声情况而设定。将原信号x(t)的时频Wx(a,b)与该阈值比较:
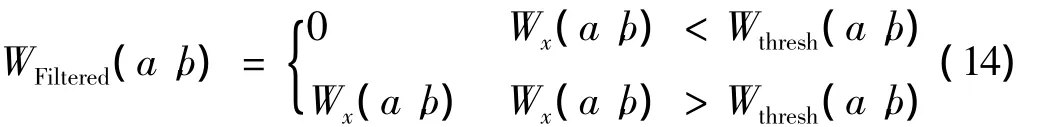
这样,在时频图上原信号的平稳成分将被滤除,同时由噪声或者泄露引起的非平稳信息也将被滤除,而保留部分就是原信号中有意义的非平稳成分,并且从时频图上可以清楚的反映出非平稳时间和频率信息。但是小波时频特性清晰度不如同步压缩变换,且方法未能恢复出时域信号。
4 振动信号平稳成分与非平稳成分的分解
利用同步压缩变换在时频分析的优势,结合局部替代数据方法,提供了一种可以将原振动信号分解为平稳成分和非平稳成分的途径。
首先将原信号x(t)利用式(6)生成N个替代数据si(t),这些替代数据具备原信号相同的边际谱,并且是平稳过程,因此可利用生成的N个替代数据在时频上的统计规律作为平稳与非平稳成分的判据,具体操作类似于前述的局部替代数据法,这里的时频分析则采用了更为精细的同步压缩变换。具体步骤如下。
对每个替代数据进行同步压缩变换Ti(f,b),对其幅度谱求均值得:
求幅度谱的标准差:

设定平稳性检验阈值:
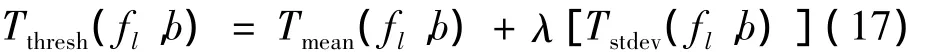
其中λ为阈值调整参数。
对原信号x(t)进行同步压缩变换并取幅度谱为Tx(f,b ),为了能滤除非平稳成分的时频信息而保留平稳成分时频信息,因此采用了与公式(14)相反的平稳性检验阈值判定条件,如式(18):
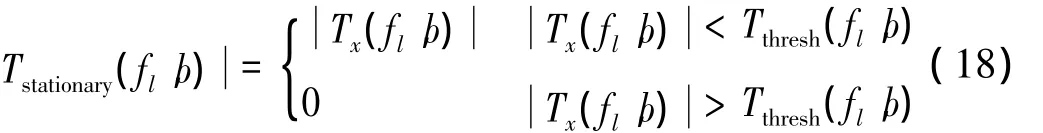
需注意,采用式(18)的判定条件,则平稳性检验阈值调整参数λ越小则滤除非平稳越多,反之则滤除非平稳越少。
由于得到的只是幅度谱,为了恢复时域信号,还必须保证留下的平稳成分的时频谱上相位与原来信号一致,因此计算原信号同步压缩变换的相位:
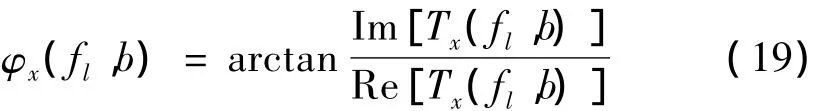
将保留的平稳成分的幅度谱和求出的相位谱合成为平稳成分的同步压缩谱:
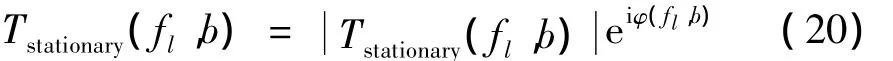
最后利用式(4)同步压缩反变换恢复出时域的平稳成分的估计x^stationary(t),采用同步压缩替代数据检测该成分是否平稳,如果不平稳则重新调整参数λ设定阈值,再重复上述过程,直至最后的平稳成分的估计x^stationary(t)满足平稳性检测。将原信号减去该平稳成分即得非平稳成分x^nonstationary(t)=x(t)-x^stationary(t)。算法流程如图2所示。

图2 算法流程图Fig.2 Algorithm flow chart
5 数值算例
算例1 分析对象为时长40 s的信号,采样频率50 Hz,仿真信号包含的平稳成分为40 s幅度为1、频率3 Hz正弦信号,非平稳成分为一段10 s幅度为1、频率为10 Hz的正弦信号,叠加一个一段10 s幅度为1的调频(FM)信号。分解结果如图3所示,其中计算出λ=2.55。其中(a)、(b)、(c)分别为原始信号、分解出的平稳成分、分解出的非平稳成分的同步压缩变换的时频图,(d)为它们时域波形比较,从上到下依次为原信号,平稳信号成分,非平稳信号成分。可见,采用本文提出的方法可将信号平稳及非平稳两部分较好的分解出来,证明了该方法对调频以及幅度变换明显的非平稳信号分解的有效性。
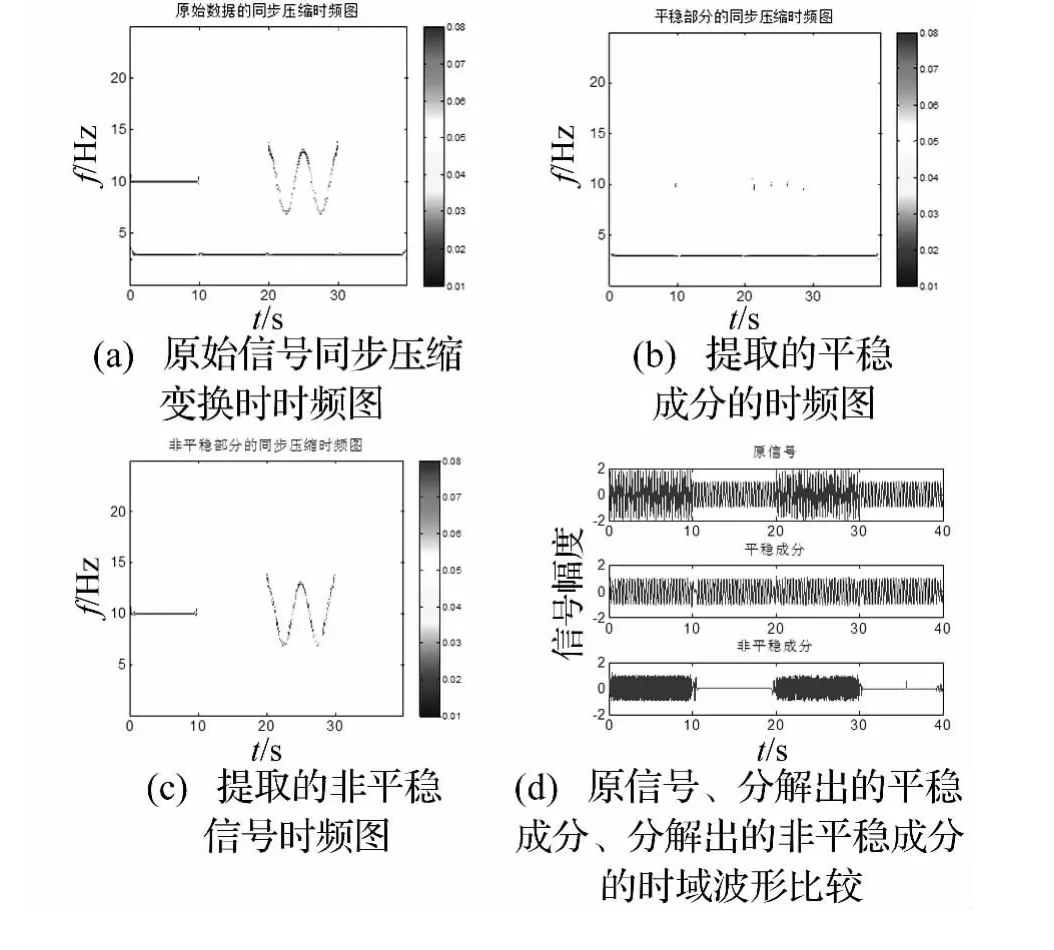
图3 正弦信号与含有明显调幅、调频信号的分解Fig.3 Decomposition of a sine signal plus a signal with apparent AM and FM
算例2 前面已经检测汶川地震波是非平稳信号,因此用该信号叠加两个幅度为1、频率分别为3 Hz和10 Hz的正弦信号,时长100 s,采样50 Hz。分解结果如图4所示,取λ=1.7。其中(a)为原始信号同步压缩变换的时频图,(b)图为分解出的平稳成分时频图,可以看出其时频谱基本不随时间变化,(c)为分解出的非平稳成分时频图,可看出频率随时间变化较大,(d)为它们时域波形比较,从上到下依次为原信号,平稳信号成分,非平稳信号成分。
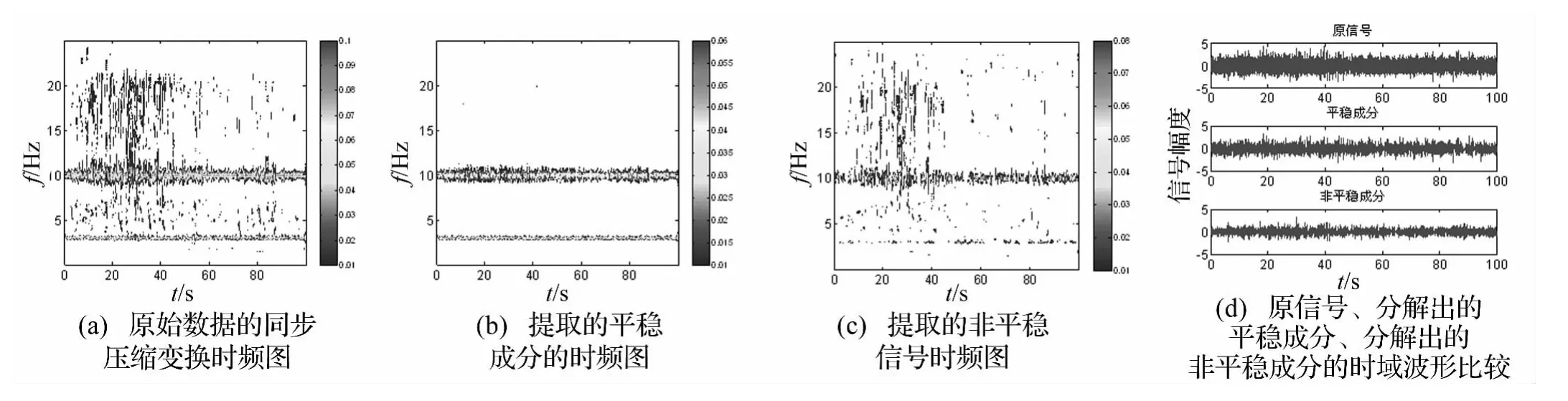
图4 两个谐波成分与汶川地震波的分解Fig.4 Decomposition of two harmonic components plus Wenchuan seismic wave
6 结论
本文提出了基于同步压缩变换所获得的清晰时频图和替代数据法相结合的信号平稳性检测方法。提出了基于同步压缩变换时频图和局部替代数据法相结合的非平稳信号分解方法。该方法通过在时频面上分析时频幅度谱的统计特性,利用平稳性检测方法确定的分解阈值,在时频图上对信号的平稳和非平稳成分进行分解;在保持原信号相位不变的基础上,采用同步压缩反变换重构出时域信号的平稳和非平稳成分。数值算例验证了所提出的信号平稳性检测方法和非平稳信号分解方法的有效性。
[1] Bünau P,Meinecke F C,Király F C,et al.Finding stationary subspaces in multivariate time series[J].Physical Review Letters,2009,103(21):21401.
[2] Xiao J,Borgnat P,Flandrin P.Testing stationarity with timefrequency surrogates[C].15th European Signal Processing Conference[C].Poznan,Poland,2007:2020-2024.
[3] Xiao J,Borgnat P,Flandrin P,et al.Testing stationarity with surrogates-A one-class SVM approach[A].IEEE Stat.Sig.Proc.Workshop SSP07[C].Madison,WI,2007.
[4]Borgnat P, Flandrin P. Time-frequency surrogates for nonstationary signal analysis[A].8th IMA International Conference on Mathematics in Signal Processing[C].Cirencester,UK,2008.
[5]Borgnat P,Flandrin P,Paul H,et al.Testing stationarity with surrogates:A time-frequency approach[J].IEEE Transactions on Signal Processing,2010,58(7):3459-3470.
[6]任伟新,韩建刚,孙增寿.小波分析在土木工程结构中的应用[M].北京:中国铁道出版社,2006.
[7]McCullough M,Kareem A.Testing stationarity with wavelet based surrogates[J].Journal of Engineering Mechanics,2012,139(2):200 -209.
[8] Daubechies I, Maes S. A nonlinear squeezing of the continuous wavelet transform based on auditory nerve models.in:A.Aldroubi,M.Unser(Eds.),Wavelets in Medicine and Biology[M].CRC Press,1996:527 546.
[9] Daubechies I,Lu J F,Wu H T.Synchrosqueezed wavelet transforms:An empirical mode decomposition-like tool[J].Applied and Computational Harmonic Analysis, 2011,30(2):243-261.
[10] Thakur G,Brevdo E,Fucˇkar N S,et al.The synchrosqueezing algorithm for time-varying spectral analysis:robustness properties and new paleoclimate applications[J].Signal Processing,2013,93(5):1079-1094.
[11] Brevdo E,Wu H T.The synchrosqueezing toolbox[EB/OL].https://web.math.princeton.edu/~ ebrevdo/synsq/,2012,6.
[12] Bendat J S,Piersol A G.Random data:analysis and measurement procedures,4 Ed.[M].John Wiley and Sons,Hoboken,NJ.,2010.
[13] Beck T W,Housh T J,Weir J P,et al.An examination of the runs test,reverse arrangements test,and modified reverse arrangements test for assessing surface EMGsignal stationarity[J].Journal of Neuroscience Methods,2006,156(1 -2):242-248.
[14] Theiler J, Eubank S, Longtin A, et al. Testing for nonlinearity in time series:the method of surrogate data[J].Physica D,1992,58:77-94.

