关节柔性的漂浮基空间机器人基于奇异摄动法的轨迹跟踪非奇异模糊Terminal滑模控制及柔性振动抑制
梁 捷 ,陈 力
(1.福州大学 机械工程及自动化学院,福州 350108;2.中国空气动力研究与发展中心,绵阳 621000)
空间机器人因其在卫星维修和回收、航天器维护和修理、空间站的构建和装配,以及代替宇航员执行危险任务中发挥的重要作用而受到人们的广泛关注,有关空间机器人系统动力学控制研究也受到各国研究人员的密切重视,并已取得了一定的成果[1-16]。随着空间技术的发展对空间机器人的要求越来越高,柔性空间机器人因其反应速度快、效率高、执行机构少、质量轻、成本低等优点而备受关注。但值得关注的是,大多数的研究仅仅考虑了空间机器人系统结构中柔性臂的存在[1,9],却忽视了关节柔性的存在,即:机械臂与装备在关节处的驱动机械臂运动的电机之间不存在绝对刚性的连接,这使得机械臂的关节也呈现出柔性的特征。对空间机器人来说,关节柔性一方面可以缓冲空间机器人在运动过程中发生的意外碰撞,降低空间机器人的损伤。另一方面会导致机械臂的转动与驱动其运动的电机转子的转动角度之间存在着转动误差,从而影响到控制系统的精度;同时,关节的柔性特性还会导致机械臂在高精度和高速的运动过程中产生振动。因此,若在漂浮基空间机器人系统动力学建模和控制方法设计过程中忽略关节柔性的存在,其控制精度和稳定性将受到很大影响。虽然目前已有科研人员对关节柔性系统进行了研究[17],但多数的研究是针对关节柔性的地面机器人的,而针对关节柔性空间机器人的研究还比较少。尤其对于关节柔性的漂浮基空间机器人系统,其本体呈现自由漂浮的状态,系统结构具有强耦合性和非线性,这使得惯常应用于关节柔性的地面机器人的一些较成熟的控制方法难以得到直接应用于推广。同时,受到负载变化、参数摄动、燃料消耗等不确定因素的影响,漂浮基空间机器人系统的动力学模型往往是不确定的。因此,对关节柔性的漂浮基空间机器人的研究难度更大、挑战性更高。
基于以上情况,本文针对具有关节柔性和不确定系统参数的漂浮基空间机器人系统,建立其动力学模型,并利用奇异摄动理论的双时间刻度分解,将系统分解为相对独立的表示系统刚性运动的慢时标子系统和表示系统柔性运动的快时标子系统。分别针对两个子系统设计相应的控制方案来保证系统的控制精度和稳定性。
1 关节柔性的漂浮基空间机器人系统动力学奇异摄动模型
不失一般性,以做平面运动且本体位姿均不受控制的关节柔性漂浮基空间机器人系统为例,几何模型如图1所示。该系统由自由漂浮的空间站本体W0,两个弹性关节Oi(i=1,2)和两个刚性机械臂W1、W2及刚性机械臂W2末端爪手抓持着的刚性载荷WP组成。
建立惯性坐标系(OXY)及分体Wi(i=0,1,2)的连动坐标系(Oixiyi),并假设系统沿(X,Y)平面作平面运动;此外,图中q0为空间站本体姿态的实际转角,qai(i=1,2)各关节驱动电机的实际转角,qi(i=1,2)为连杆Wi的实际转角。
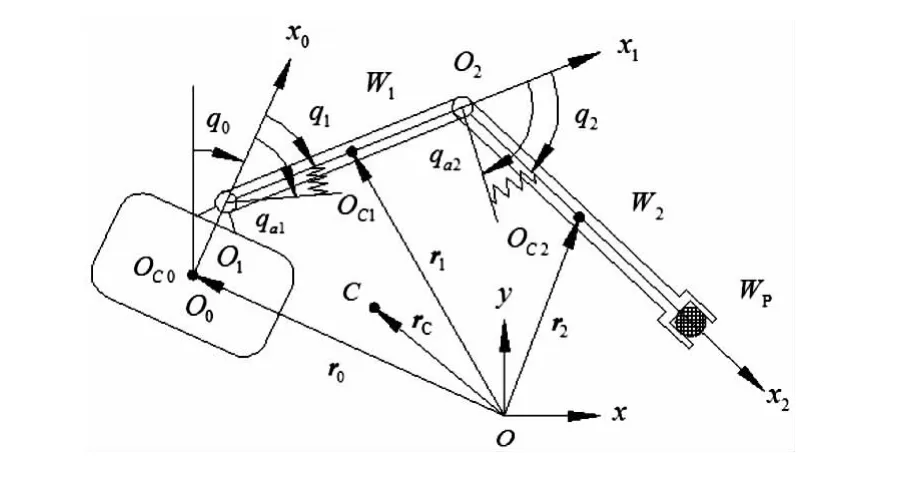
图1 关节柔性的漂浮基空间机器人系统Fig.1 Free-floating space robot with flexible joints
文中所使用的符号约定如下:m0、I0、l0分别为本体的质量、转动惯量及其质心到第1个关节铰中心的距离;mi、Ii、li分别为刚性机械臂 Wi(i=1,2)的质量、转动惯量及其长度;mP、IP分别为末端刚性载荷WP的质量及转动惯量;由于载荷WP是由机械臂W2末端爪手抓持着,因此可将机械臂W2与载荷WP看成一联合体,该联合体的总质量和总转动惯量为m2P、I2P;Iai为柔性关节i(i=1,2)驱动电机的等效转动惯量、Ki(i=1,2)为各关节铰的扭转刚度;r0、r1分别为载体及连杆1质心的位置矢量,r2为连杆2与末端负载联合体质心的位置矢量,rC、rP分别为系统总质心及负载质心的位置矢量。各分体Wi(i=0,1)的转动角速度为vi,机械臂W2与载荷WP的联合体的转动角速度为vp=v2,关节Oi(i=1,2)处电机转子的自转角速度为vai。
1.1 柔性关节简化模型
根据文献[18]的假设,柔性关节可简化为图2所示刚度系数为k的无惯量线性扭簧,这意味着电机转子与机械臂之间的联接为柔性,当关节Oi处的电机转子转过角度qai时,受其驱动的机械臂Wi由于扭簧弹性力的作用,其转动角度为:qi=qai-ai,其中ai为柔性关节引起的转动误差。电机转子与机械臂之间弹性作用力的大小为ki(qai-qi)。此时,若仍然采用常规的方法(即将关节驱动电机和机械臂视为纯刚性连接的整体)进行系统动力学模拟和控制方案设计,必将不断累积刚-柔性转角误差ai,从而影响系统的控制品质。基于以上讨论,在对关节柔性的漂浮基空间机器人系统进行动力学分析时,必须分别讨论空间机器人的动力学和电机转子的动力学。
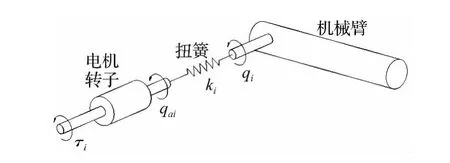
图2 柔性关节的简化模型Fig.2 Simple model of flexible-joint
1.2 系统动力学方程的建立
由系统总质心定义及位置几何关系,可导出
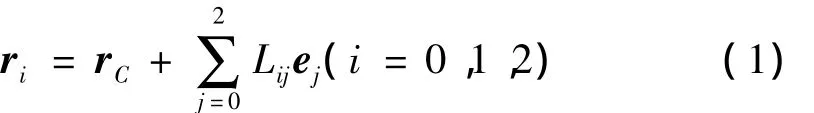
其中:Lij(i=0,1,2;j=0,1,2)均为系统惯性参数的组合函数,ej为xj轴的基矢量。
由于考虑了关节柔性的存在,因此,系统的总动能T应该由空间机器人的动能Tr和电机转子动能Ta之和组成。而由于电机转子的质量可忽略不计[18],故电机转子的动能主要为其自转动能。于是系统的总动能可表示为:

在宇宙环境中,忽略微弱的重力作用,系统的总势能仅为柔性关节简化扭簧的弹性变形势能,即:
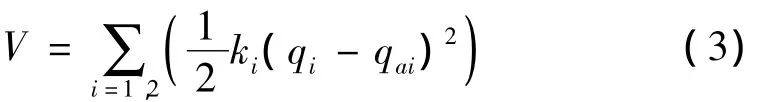
其中:常数ki(i=1,2)为线性弹簧的等效扭转刚度。
由于本体位置、姿态均不受控的关节柔性的漂浮基空间机器人系统为无外力作用的自由漂浮无根多体系统,系统相对于惯性坐标系(OXY)满足动量、动量矩守恒关系。不失一般性,假设系统的初始动量、动量矩为零,即=0,于是系统的动量、动量矩守恒关系可表示为:
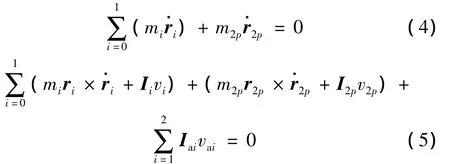
利用式(1)~(5)及拉格朗日法,可解得载体位置、姿态均不受控的关节柔性的漂浮基空间机器人系统完全驱动形式的动力学方程:
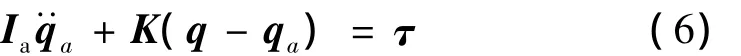
M(q0,q)q··+h(q0,q,q·,q·a)-K(q-qa)=0(7)其中:式(6)为电机转子的动力学方程,式(7)为空间机器人的动力学方程;Ia=diag(Ia1,Ia2)为驱动电机转子的对角正定惯量矩阵;q=[q1q2]为空间机器人的转角矩阵;qa=[qa1qa2]为驱动电机转子的转角矩阵;M(q0,q)∈ℜ2×2为空间机器人的正定、对称惯性矩阵;h(q0,q)包含科氏力、离心力的2阶列向量;K=diag[k1k2]为对角形式的系统刚度矩阵,ki(i=1,2)为各关节的线性扭转刚度;τ= [τ1τ2]为由于关节柔性所产生的连杆驱动力矩列向量。
1.3 系统动力学方程的奇异摄动模型
由于关节柔性的存在会影响系统的控制精度和并引起系统弹性振动,同时还会给系统带来刚-柔性转角误差。因此,为了实现对关节柔性的漂浮基空间机器人系统期望运动轨迹的跟踪和关节柔性振动的主动抑制,本文基于奇异摄动法,将系统动力学方程式(6)和式(7)近似地分解为相互独立的表示系统刚性运动部分的慢时标子系统和表示系统柔性运动部分的快时标子系统,并分别为子系统设计合适的控制算法。其中,慢时标子系统控制律τs用来实现系统期望运动轨迹的渐近跟踪;快时标子系统控制律τf用来抑制柔性关节引起的系统柔性振动,保证系统的稳定性。于是系统总控制律表示为:

假设存在很小的正比例因子ε和正定对角阵K1=ε2K。并定义q为慢变量,弹性力z=K(q-qa)为快变量。则系统动力学方程式(6)和式(7)可重新写为
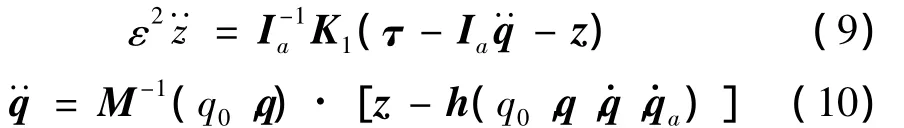
设计快时标子系统基于速度差值的反馈控制律:

其中:Kf=K2/ε,K2为正定对角阵。从上式可看出,通过反馈回的速度差值来不断调节Kf来保证系统的稳定。
将式(8)和式(11)代入式(9),可得快时标子系统的动力学方程

由K=K1/ε2可知:当ε→0时,K→∞,电机转子和刚性杆之间的联接可近似等效为刚性,即qa=q、z=0。于是,由式(6)和式(7)可解得慢时标子系统的动力学方程:
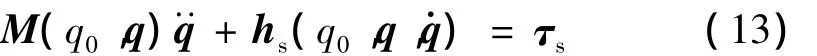
其中:hs(q0,q,q·)为令h(q0,q,q·,q·a)中q·a=q·后所得到的简化列向量。
为了控制系统设计的需要,将方程式(13)作准线性化处理[19],写作:
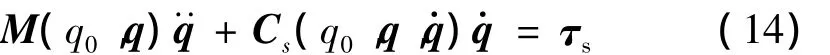
这种准线性化处理只是式子表现形式发生了变化,没有产生任何模型精度损失。综上所述,式(12)和式(14)描述的即为关节柔性的漂浮基空间机器人系统的奇异摄动数学模型。下面将基于式(14)所描述的慢时标子系统动力学方程,设计慢时标子系统控制律 τs。
2 慢时标子系统的控制器设计
由于本身结构的复杂性,空间机器人系统的某些惯性参数(如燃料消耗会导致系统质量变化、机械臂的长度、负载的质量等)是难以精确确定或未知的,同时被捕获的敌方各类卫星系统的惯性参数通常也是未知的,因此方程式(14)中M(q0,q)、Cs(q0,q,q·)q·可表示为:
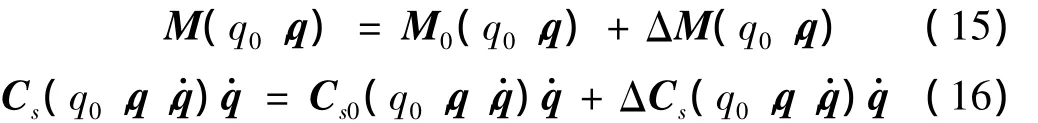
其中,M0(q0,q)、Cs0(q0,q,分别为M(q0,q)、Cs(q0,q在标称系统动力学参数下的估计,ΔM(q0,q)和ΔCs(q0,q,为系统参数不精确估计所引起的建模误差。因此,基于以上讨论,建立了适用于关节柔性的空间机器人控制系统设计的数学模型
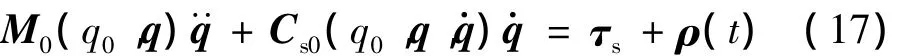
其中:τs为针对该数学模型的控制器,将在下一节中进行设计。
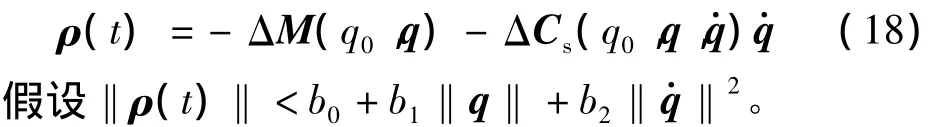
近年来,Terminal滑模控制器由于相对于传统线性滑模控制器具有更高的稳态跟踪精度以及能在有限时间内收敛等优点而研究引起了人们的重视[20]。但现有的Terminal滑模控制中存在奇异区域的缺点[21]。针对以上Terminal滑模控制存在的不足,本节利用适用于关节柔性的空间机器人控制系统设计的数学模型式(17),提出了一种非奇异模糊Terminal滑模控制方案,来获得关节柔性的空间机器人系统惯性参数存在未知的情况下,上述控制系统对期望轨迹渐近稳定的跟踪控制效果。
2.1 非奇异Terminal滑模控制器设计
令qd=[qd1qd2]T为慢时标子系统期望输出向量,则其与实际输出向量q=[q1q2]T之间的误差向量为:e=q-qd,速度误差向量为
为了解决普通Terminal滑模控制的奇异问题,提出了非奇异Terminal滑模控制,非奇异滑模面为:

其中:滑模面常数 λ =diag[λ1,λ2];p、q 为奇数,且1<p/q<2。
非奇异Terminal滑模控制器设计为:

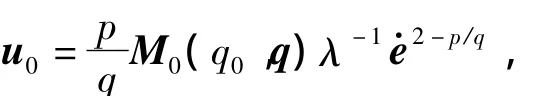
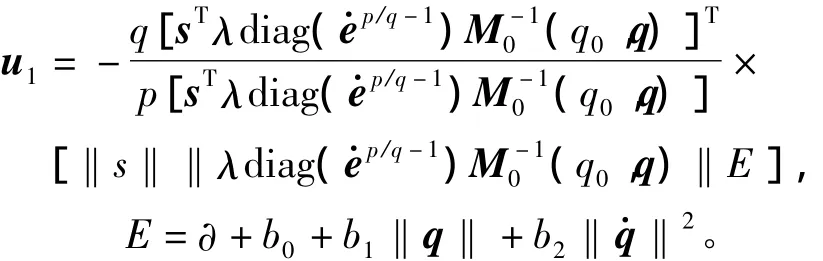
其中:∂>0是正常数。需要指出的是,虽然上述控制器能够保证系统稳定并使跟踪误差在有限的时间内收敛到零,但其设计存在的明显不足是:该控制器要求建模误差ΔM(q0,q)和ΔCs(q0,q,q·)q·的上界E是已知的,而这在实际的慢时标子系统控制中很难做到,所以出于充分补偿建模误差的需要,设计时一般选择的E值都较大,这样又加剧了非奇异Terminal滑模控制器的抖振。因此,文中针对上述控制器设计的缺陷,附加设计了一个模糊自适应控制器,该控制器能够根据滑模面s和s·自动调整E值补偿系统的建模误差,从而大大减小了控制器的抖振,并保证了系统稳定。控制器设计如下。
2.2 基于非奇异Terminal滑模面的模糊自适应控制器设计与稳定性分析
对于一个模糊推理系统(该系统具有p个输入、1个输出、n条If-then模糊规则),若采用模糊单值产生器,乘积推理规则,加权平均去模糊化方法,则模糊逻辑系统的输出为:
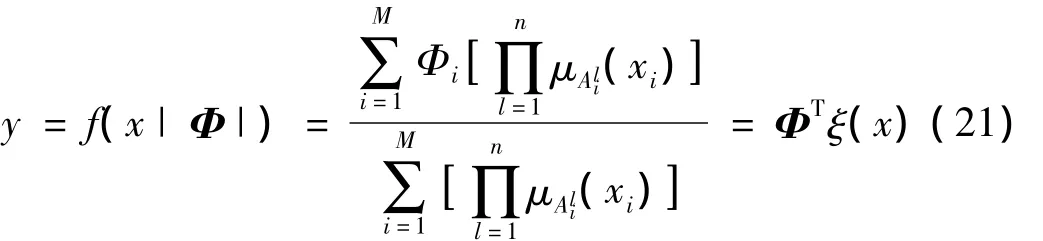
其中:n为模糊系统第i条模糊规则有关的输入向量个数,且有1≤n≤p;模糊系统第i条模糊规则中第l个输入的隶属度函数为μAli(xi),且有 1≤l≤n;Φ =[Φ1,Φ2,…,ΦM]T为模糊系统的自适应参数矢量;ξ(x)=[ξ1(x),ξ2(x),…,ξM(x)]T为模糊基函数矢量,ξi=
文献[22]用Stone-Weierstrass定理证明了模糊逻辑系统f(x)能够以任意精度逼近紧致集上的任意连续实函数h(x),并提出了模糊基函数(FBF)的概念。因此,可用模糊逻辑系统对关节柔性的空间机器人慢时标子系统建模误差进行辨识。文中模糊自适应控制就是设计如式(21)所示的模糊逻辑系统的自适应律Φ·,使得模糊系统随着被控对象的变化而变化。
设慢时标子系统系统关节i(i=0,1,2)的建模误差ρi(t)存在上界,即‖ρi(t)‖≤Ei,则定义自适应模糊控制器的最优逼近参数是:
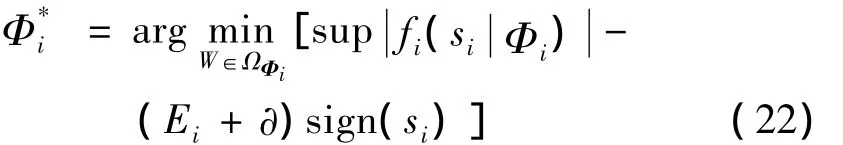
定义最小逼近误差:
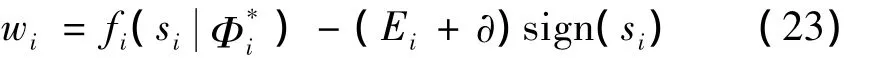
则由式(23),模糊自适应控制器的最优输出可表示为:
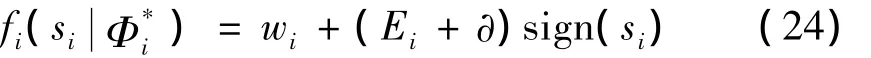
因此,模糊自适应控制器的最优参数与实时参数的误差可表示为:


其中:ri为自适应系数。
定理 针对式(17)描述的关节柔性的空间机器人慢时标子系统,采用式(19)的非奇异Terminal滑模面及式(26)的参数Φ~i的自适应调节律,控制输入规律:

可保证系统的跟踪误差e、e·一致最终有界。其中:
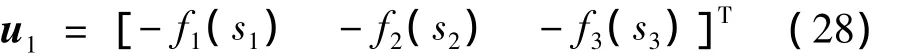
其中:fi(si)为关节i(i=0,1,2)的模糊自适应控制器输出。
证明 选择如下正定函数V作为准Lyapunov函数
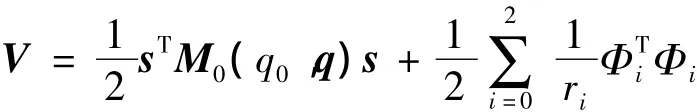
将正定函数V对时间t求导,得到:
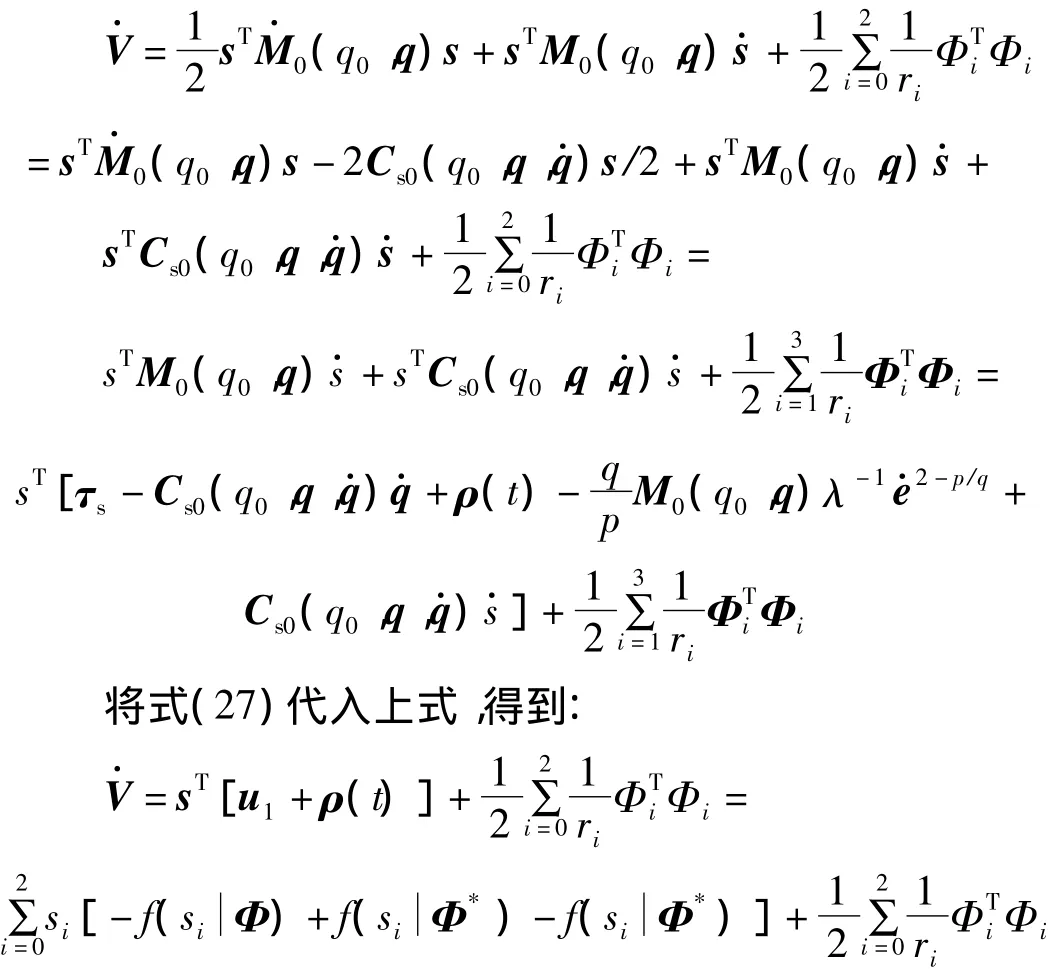
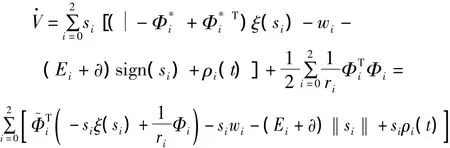
将式(21)和式(24)代入上式,有:i(i=0,1,2)的模糊自适应控制器输出fi(si)与逼近函数的误差wi可以任意小,因此可忽略,得到:
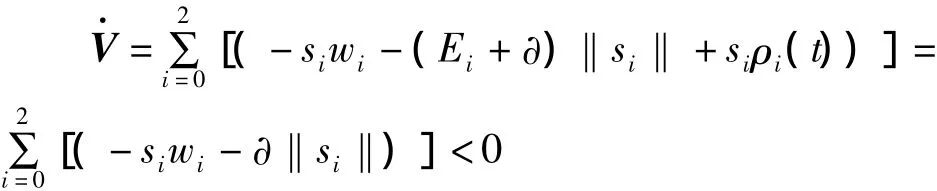
因此,所设计的基于非奇异Terminal滑模面的模糊自适应控制系统是渐近稳定的。
3 仿真算例与分析
针对图1所示的关节柔性的漂浮基空间机器人系统,利用本文所提的控制方案式(11)、式(27)及式(26)给出的自适应调节规律进行仿真实验。设机械臂Bi(i=1,2)沿xi轴的长度为3 m,关节O1与空间站本体质心O0的距离为1.5 m,机械臂B1的质心与关节O1的距离为2 m。机械臂B2和末端载荷WP的联合体质心与关节O2的距离为1.5 m。各分体质量和惯量矩分别为:m0=40 kg,m1=2 kg,m2=1 kg;I0=34.17 kg·m2,I1=1.5 kg·m2,I2=0.75 kg·m2;目标物体的质量为mP=2 kg,中心惯量张量为IP=1 kg·m2。第一个柔性关节驱动电机的等效转动惯量及其关节刚度分别为 I1m=0.09 kg·m2和 k1=200.0 N·m/rad;第二个柔性关节驱动电机的等效转动惯量及其关节扭转刚度分别为 I2m=0.04 kg·m2和 k2=100.0 N·m/rad;仿真时,假定机械臂末端载荷WP的质量及中心转动惯量矩为不确定系统惯性参数,其不确定范围为3.0 kg≥mP≥0.0 kg,5.0 kg·m2≥IP≥0.0 kg·m2。并假设空间机器人运动转角的期望轨迹为:
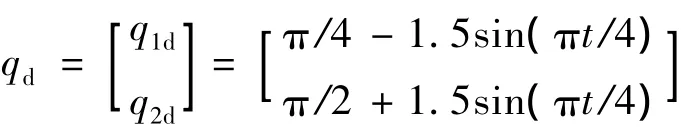
同时,控制系统相关参数选取如下:λ=diag[65,65],q=3,p=5,r0=r1=r2=0.1,K2=diag[0.35,0.35],ε =0.01,Kf=diag[35.0,35.0]。
将电机转子转角与空间机器人的期望转角之间的差值表示为:ea=qa-qd。系统运动初始值为:q0=0.05,q= [0 .2 2.2 ],qa= [0 .2 2.2],单 位 均 为(rad)。仿真时间:t=15 s。
仿真结果如图3~图6所示。其中图3为空间机器人转角的期望运动轨迹(实线)与实际运动轨迹(虚线)的对比图;图4为空间机器人转角运动的跟踪误差图;图5为电机转子转角与空间机器人期望转角的差值的跟踪轨迹图;图6为关闭模糊自适应控制器u1情况下空间机器人转角运动的轨迹图;图7为关闭快时标子系统控制律τf情况下,电机转子转角与空间机器人期望转角的差值的跟踪轨迹图。
由文献[22]中的Stone-Weierstrass定理可知,关节
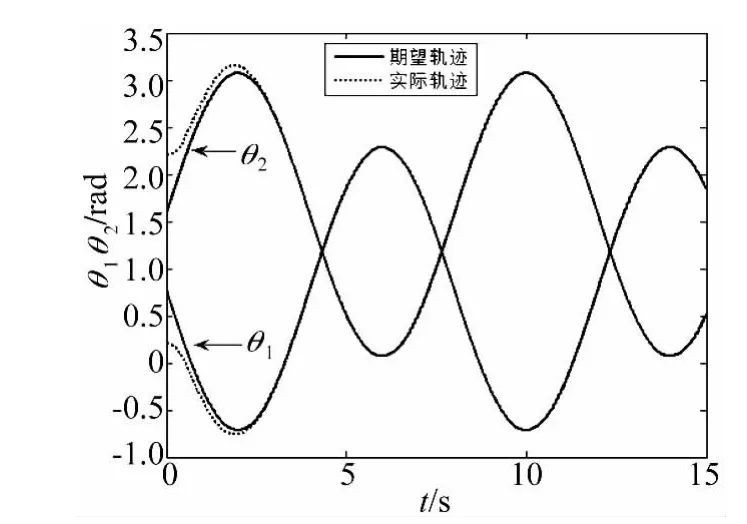
图3 空间机器人转角的运动轨迹Fig.3 The motion trajectories of space robot
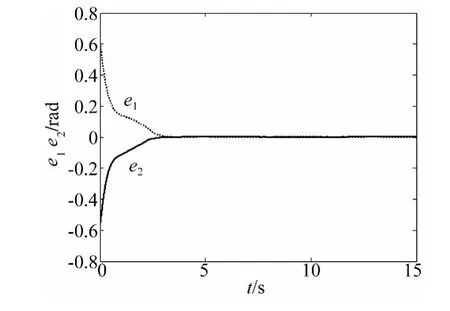
图4 空间机器人转角运动的跟踪误差eFig.4 The tracking error e
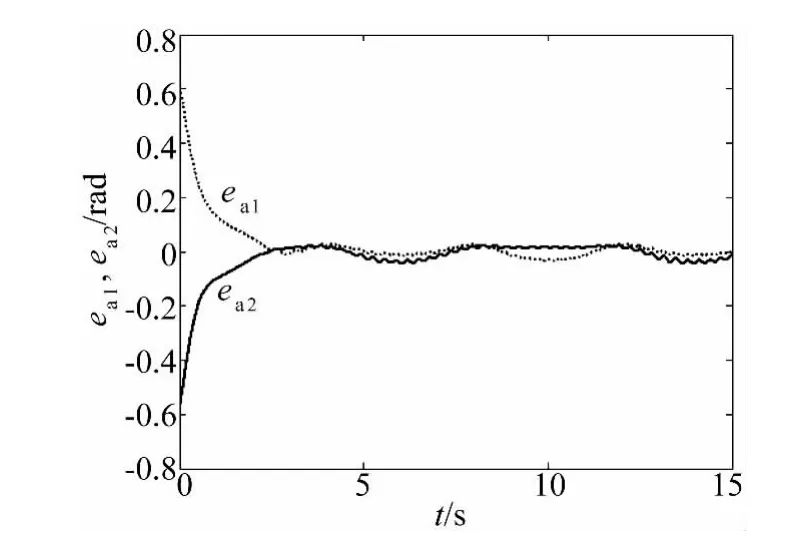
图5 电机转子转角与空间机器人期望转角的差值eaFig.5 The difference ea
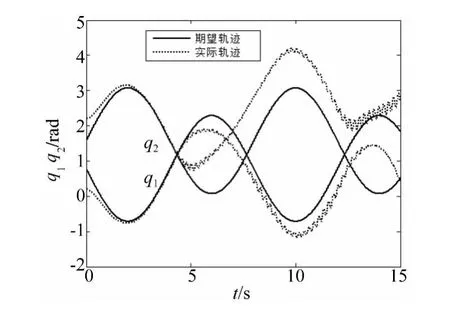
图6 关闭模糊自适应控制器u1情况下空间机器人转角运动轨迹Fig.6 The motion trajectories of space robot when the fuzzy adaptive controller is closed
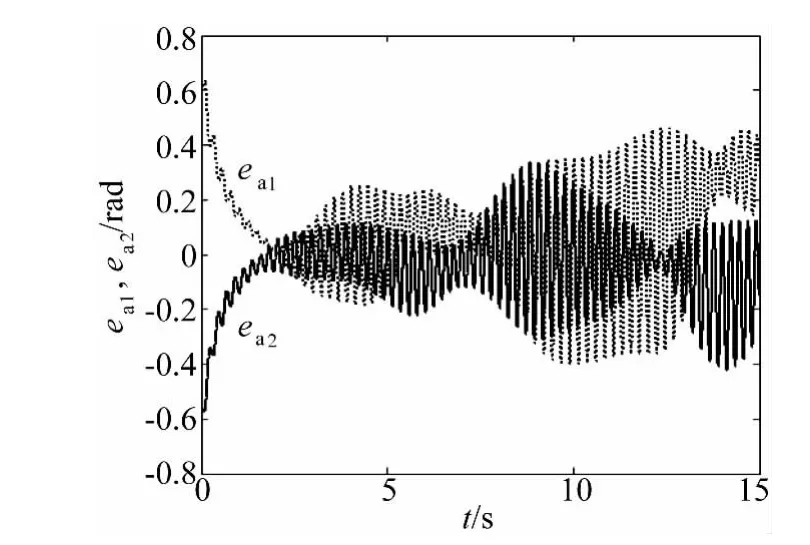
图7 关闭快时标子系统控制律τf情况下电机转子转角与空间机器人期望转角的差值e aFig.6 The motion trajectories of space robot when τf is closed
由图3~图5可以看出,在本文设计的控制方案控制下,电机转子和空间机器人的转角实际运动轨迹都能够精确且稳定地跟踪上同一期望运动轨迹。这说明本文提出的控制方案能够消除因关节的柔性而引起的系统“刚-柔转角误差”,补偿系统参数的不确定性。图6可看出,关闭模糊自适应控制器u1情况下,控制系统精度变差且运动过程中存在抖振,这个抖振正是由非奇异Terminal滑模控制自身造成的,从而证明了模糊自适应控制器u1可有效补偿系统不确定性。从图7可看出,关闭快时标子系统控制律τf情况下(即未对由关节的柔性引起的系统弹性振动进行主动抑制),电机转子转角与空间机器人期望转角转角的差值ea在2s左右就已经变得很大,控制失效,因此关节的柔性对空间机器人的影响是非常大的,也说明了本文提出的快时标控制器对弹性振动采取的主动抑制是非常必要和有效的。
4 结论
本文讨论了考虑关节柔性、参数不确定的漂浮基空间机器人系统的动力学建模过程,并基于奇异摄动法建立了系统的奇异摄动模型,提出了慢时标子系统的控制方法和快时标子系统的速度差值反馈控制方法组成的混合控制方法。数值仿真实验表明,本文提出的控制方法能够抑制关节柔性引起的系统弹性振动,保持控制系统的稳定性;同时还能够有效消除关节柔性带来的系统“系统刚-柔性转角误差”,补偿系统参数的不确定性,实现漂浮基空间机器人运动轨迹的渐近跟踪。由于在系统动力学方程推导过程中充分利用了带柔性铰空间机器人的动力学特性,与文献[11-14]的控制方法相比,提出的方法在控制过程中不需要反馈、测量漂浮基的位置、移动速度、移动加速度以及载体姿态转角的角速度、角加速度,从而使得提到的控制方案更切合于实时、在线应用。
[1]Kumar A,Pathak PM,Sukavanam N.Reduced model based control of two link flexible space robot[J].Intelligent Control and Automation,2011,2:112-120.
[2]Steve U,Jurek Z S.Extended kalman filtering for flexible joint space robot control[C]//2011 American Control Conference.San Francisco.CA.USA:IEEE.2011:1021-1026.
[3] Nanos K.On the use of free-floating space robots in the presence of angular momentum [J].Intelligent Service Robotics,2011,4(1):3-15.
[4]Abiko S,Hirzinger G.An adaptive control for a free-floating space robot by using inverted chain approach[C]//Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems,San Diego,CA,USA:IEEE Press,2007:2236-2241.
[5]Parlaktuna O,Ozkan M.Adaptive control of free-floating space manipulators using dynamically equivalent manipulator model[J].Robotics and Autonomous Systems,2004,46(3):185-193.
[6]洪在地,贠 超,陈 力.柔性臂漂浮基空间机器人建模与轨迹跟踪控制[J].机器人,2007,29(1):92-96.HONG Zai-di, YUN Chao, CHEN Li. Modeling and trajectory tracking control of a free-floating space robot with flexible manipulator[J].Robot,2007,29(1):92-96.
[7]戈新生,陈立群,吕 杰.空间机械臂非完整运动规划的遗传算法研究[J].宇航学报,2005,26(3):262-266.GE Xin-sheng,CHEN Li-qun,LÜ Jie.Nonholonomic motion planning of a space manipulator system using genetic algorithm [J].Journal of Astronautics,2005,26(3):262-266.
[8]王从庆,石宗坤,袁 华.自由浮动空间双臂机器人的鲁棒协调控制[J].宇航学报,2005,26(4):436-440.WANG Cong-qing,SHI Zong-kun,YUAN Hua.Robust coordinated control of a free-floating dual-arm space robot[J].Journal of Astronautics,2005,26(4):436-440.
[9]章定国.多杆空间柔性机器人递推Lagrange动力学建模和仿真[J].应用数学和力学,2009,30(10):1202-1212.ZHANG Ding-guo.Recursive lagrangian dynamic modeling and simulation of multi-link spatial flexible manipulator arms[J].Applied Mathematics and Mechanics,2009,30(10):1202-1212.
[10]丁希仑,俞玉树.一种多旋翼多功能空中机器人及其腿式壁面行走运动规划[J].航空学报,2010,31(10):2075-2086.DING Xi-lun,YU Yu-shu.A multi-propeller and multifunction aero-robot and its motion planning of leg-wallclimbing[J].Acta Aeronouticaet Astronautica Sinica,2010,31(10):2075-2086.
[11] Gu Y L,Xu Y S.A normal form augmentation approach to adaptive control of space robot systems[J].Journal of the Dynamics and Control,1995,5(3):275-294.
[12] Xu Y S,Shum H Y,Kanade T,et al.Parameterization and adaptive control of space robot systems[J].IEEETransactions on Aerospace and Electronic Systems(S0018-9251),1994,30(2):435-451.
[13] Walker M W,Wee L B.Adaptive control of space-based robot manipulators[J].IEEE Transactions on Robotics and Automation(S1042-296X),1991,7(6):828-835.
[14]陈 力,刘延柱.漂浮基空间机器人协调运动的自适应控制与鲁棒控制[J].机械工程学报,2001,37(8):18-22.CHEN Li, LIU Yan-zhu. Adaptive and robust control schemes of coordinated motion of space-based robot system[J].Chinese Journal of Mechanical Engineering,2001,37(8):18-22.
[15]梁 捷,陈 力.具有时延的漂浮基空间机器人基于泰勒级数预测、逼近的改进非线性反馈控制[J].航空学报,2012,33(1):163-169.LIANG Jie,CHEN Li.Improved nonlinear feedback control for free-floating space-based robot with time-delay based on predictive and approximation of taylor series[J].Acta Aeronouticaet Astronautica Sinica,2012,33(1):163-169.
[16]梁 捷,陈 力.基于标称计算力矩控制器的双臂空间机器人惯性空间轨迹跟踪的模糊自适应补偿控制[J].工程力学,2010,27(11):221-228.LIANG Jie,CHEN Li.Fuzzy logic adaptive compensation control for dual-arm space robot based on computed torque controller to track desired trajectory in inertia space[J].Engineering Mechanics,2010,27(11):221-228.
[17] Dong H K,Chan S P.Adaptive robust control design and experimental demonstration for flexible joint manipulators[J].Journal of Mechanical Science and Technology, 2007,21(1):57-73.
[18] Spong M W.Modeling and control of elastic joint robots[J].Journal of Dynamics Systems,Measurement,and Control,1987,109:310-319.
[19] Slotin J E,Li W P.On the adaptive control of robot manipulators[J].J.Robot.Res.,1987,6(3):49-59.
[20] Bhat SP,Bernstein D S.Finite-time stability of homogeneous systems[A].Proc of the American Control Conf[C].Albuquerque,1997:2513-2514.
[21]Wu Y,Yu X,M an X.Terminal sliding mode control design for uncertain dynamic systems[J].Systems and Control Letters,1998,34(5):281-288.
[22] Wang L X.Stable adaptive fuzzy control of nonlinear systems[J].IEEE Trans.Fuzzy System,1993,1(2):146-155.

