高阶单步法的非线性误差传递效应分析

栾强利，陈章位，文 祥

(浙江大学 流体动力与机电系统国家重点实验室，杭州 310027)

拟动力试验广泛应用于各类建筑结构的抗震性能研究，试验过程误差的大小会影响到试验结果的可靠性，因此在试验过程中我们需要对拟动力试验的误差进行有效控制。拟动力试验过程中，对试验误差的有效控制一方面可以通过采用高精度的试验设备降低试验误差，另一方面可以通过选择合适的数值积分方法减少试验过程中每一步误差的累积，因此，一个优秀的数值积分方法应该具有较小的误差传递效应，从而有效控制试验结果的准确性［1－2］。

高阶单步法是由王焕定等［3］于1996年提出，具有高精度、无条件稳定的特性，已经应用于非线性结构动力反应的时程分析;崔雪娜等［4］在高阶单步法的研究基础上，对在结构刚度为时间解析函数时高阶单步法的适用性进行了研究。本文在前人研究的工作基础上，进一步研究了系统结构刚度解析表达时系统刚度及算法参数β的变化对高阶单步法稳定性及其数值阻尼的影响，另一方面，通过采用两步累积误差迭代的方法，研究高阶单步法的误差传递效应，进一步验证了算法的数值阻尼对系统积分累积误差的影响。

1 高阶单步法

非线性动力方程可以表示为:

将其写成状态方程的形式为:

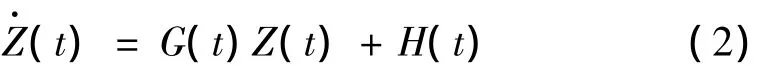
其中:

高阶单步β法在t=t0+(n+1)Δt时刻由位移、速度组成的状态向量Zn+1可由下式计算［3］:

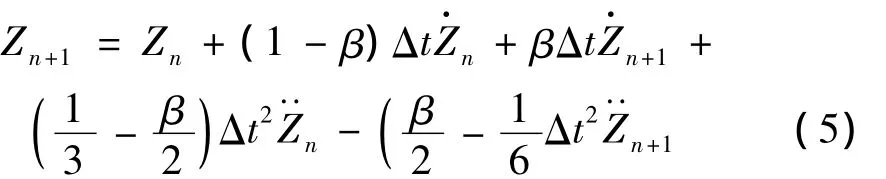
考虑到非线性动力方程中参数的时间相关性，则

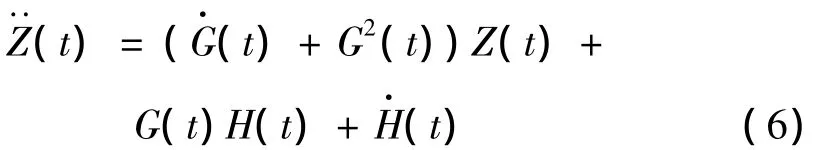
其中:

将式(6)、(7)代入式(5)并进行化简，得到:

其中:

对于离散载荷

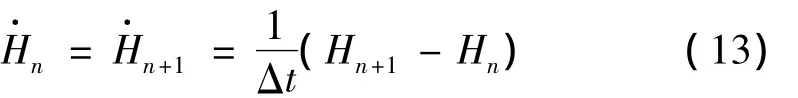
将式(13)代入式(8)并整理得:

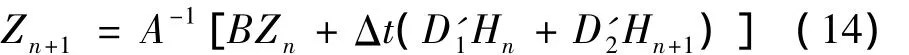
其中:

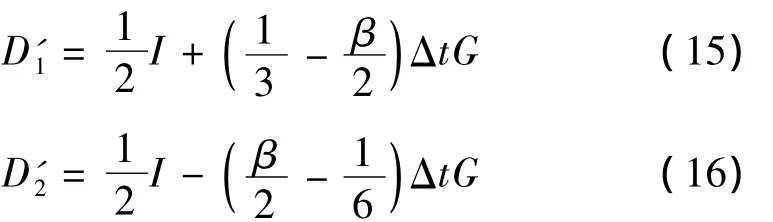
根据式(14)，第n+1时间步的位移和速度与第n时间步的位移和速度有关。

2 高阶单步法的稳定性及其数值阻尼分析

2.1 算法的稳定性分析

研究高阶单步法的稳定性及其数值阻尼在非线性系统中的影响因素，忽略系统的物理阻尼，同时考虑系统刚度的变化，参考文献［5－7］提出的刚度非线性系数模型:

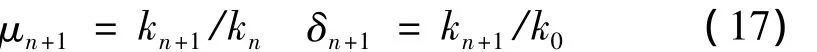
对于非线性系统其结构刚度k是变化的，为了能够评价系统中结构刚度的变化，模型中引入非线性系统离散模型的结构刚度变化系数μn+1，同时将系统的结构刚度变化解析方程表示为:

进一步得到离散系统的刚度变化系数

当刚度变化系数μn+1＞1时，结构存在刚度硬化，当刚度变化系数μn+1＜1时，结构发生刚度软化，当μn+1=1时，结构为刚度常量，本文在研究刚度变化系数对算法稳定性及其数值阻尼的影响过程中，刚度变化系数取值0.8，1.0 和 1.2，分别对应系统结构刚度软化、刚度常量以及刚度硬化情况。

将系统频率［8］的概念代入式(17)，整理得到

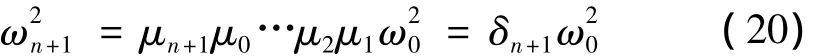
将式(20)代入式(4)、(7)、(9)和(10)得到

其中:

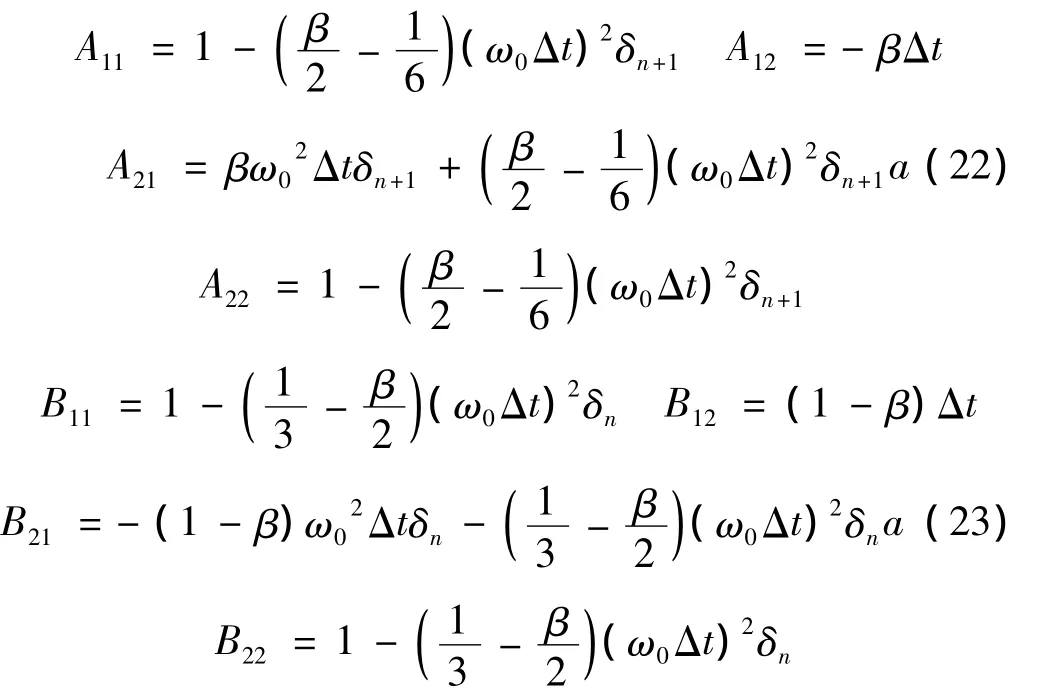
系统放大矩阵

对应特征方程为

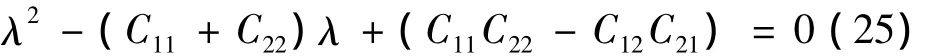
Cij(i，j=1，2)为放大矩阵对应的元素，相应的矩阵谱半径 ρ(C)=max{|λi|，i=1，2}，是关于 a、δn、δn+1、Δt、β、ω0的函数。通过数值分析验证，式(25)的判别式

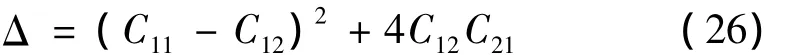
判别式的结果与刚度变化系数μn+1及β等的取值有关，但总是小于0的，因此放大矩阵的谱半径可表示为:

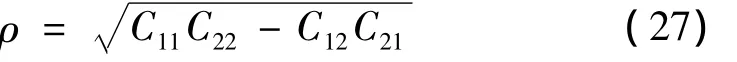
根据文献［3］得到的结论，算法无条件稳定的条件是β≥0.5，因此首先考虑在 β =0.5时，刚度变化系数对系统稳定性的影响，三种刚度变化模型对应的各自谱半径随结构频率ω0的变化规律如图1所示，当μn+1=0.8，δn+1=0.8n+1时，结构刚度软化，在 n=2 的情况下进行分析，放大矩阵的谱半径始终大于1，使得计算结果发散，即积分算法不稳定;当 μn+1=1.0，δn+1=1.0时，结构刚度为常量，其谱半径恒等于1，算法临界稳定;当 μn+1=1.2，δn+1=1.2n+1，时，结构刚度硬化，对应谱半径小于1，算法无条件稳定。进一步研究发现在μn+1=0.8，n=2刚度软化的情况下，调节β值，发现当β取值为0.518 6时，算法临界稳定，如图2所示，此时对应的其余两种刚度变化情况，算法均能实现无条件稳定，因此，对于刚度软化情况下导致的算法不稳定状态，可以通过调节β的取值实现算法的稳定。在本文研究的预设条件下，对于系统刚度软化情况，临界稳定状态 β的取值与 n和 μn+1取值的关系如表1，表2所示。

表1列出在μn+1=0.8时，为保证算法的无条件稳定，β的最小取值与对应的n取值的关系，表中n的取值范围是在0～25之间，临界稳定状态下β的变化范围为0.518 5～0.53，且β的取值随着n值的增大逐渐增大，当n过大时，结构刚度接近于零，这种情况在实际试验过程中是不存在的，因此对n值在讨论范围之外的情况未作进一步讨论。表2表示在n=2时，为保证算法的无条件稳定，β的最小取值与对应的μ值之间的关系，当μ在0.4～1.0之间变化时，β的取值是随着μ取值的增大逐渐减小的，当μ的取值为1.0时，系统的结构刚度为常量，β的算法稳定临界取值为0.5，这也验证了文献［3］中关于β在结构刚度为常量情况下，其对于算法稳定性的取值条件，即β≥0.5，在μ的取值小于0.4时，系统结构刚度过小，因此未作进一步讨论。

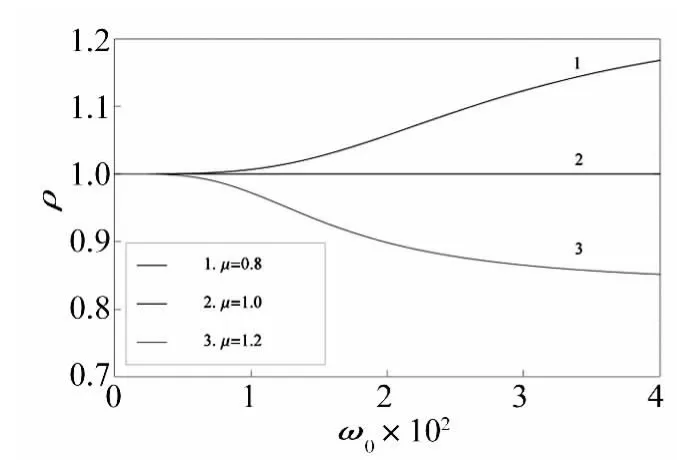
图1 β=0.5时不同刚度变化系数下ρ－ω0关系Fig.1 Numerical relationship between ρandω0 under different stiffness variation coefficients with β=0.5

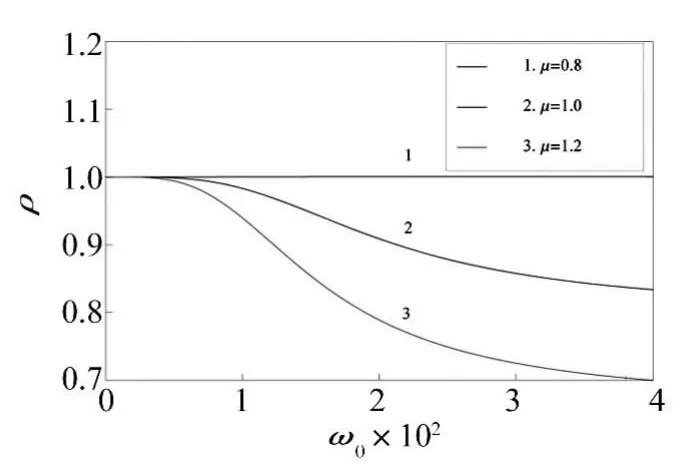
图2 β=0.518 6时不同刚度变化系数下ρ－ω0关系Fig.2 Numerical relationship between ρandω0 under different stiffness variation coefficients with β=0.518 6

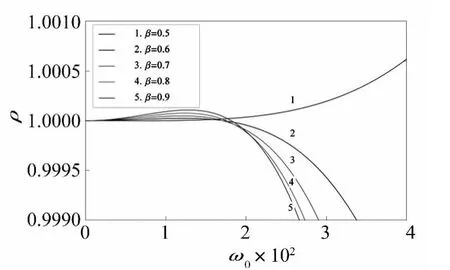
图3 μ=0.8，n=20时不同 β取值下ρ－ω0关系Fig.3 Numerical realationship betweenρandω0 under differentβ with μ =0.8 and n=20

对于表1中在μ=0.8，n=20时，不同的β取值对谱半径的影响如图3所示，当ω0的取值大于180时，随着β取值的增大，谱半径ρ(C)发生迅速衰减，实验证明，同样的变化规律发生在n(n≤25)取不同数值的情况下，即β值越大，谱半径ρ(C)衰减越快。

表1 μ=0.8时临界β值与n的对应关系Tab.1 Numerical relationship between the thresholdβand n withμ=0.8

表2 n=2时临界β值与μ的对应关系Tab.2 Numerical relationship between the thresholdβandμwith n=2

2.2 算法的数值阻尼分析

拟动力试验过程中的累积误差是随着试验结构频率的增加而不断增长的，即高频响应对试验的累积误差影响较大［9－11］，因此带有数值耗散功能即数值阻尼的积分方法可以用来有效抑制或消除算法中随结构高频响应增加的累积误差即降低算法的误差传递效应。系统放大矩阵的特征值可以表示为［8］:

其中:

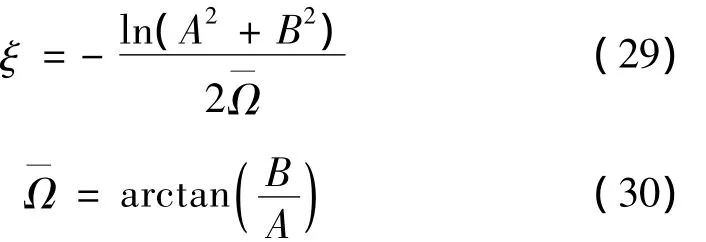
自由振动条件下，结构的位移响应可以表示为:

将式(28)代入上式，并令:

则结构的位移响应为:

因此，位移响应的大小主要取决于式(33)中右端的第一项因子(第二项为有限值)，进一步化简式(33)得到:

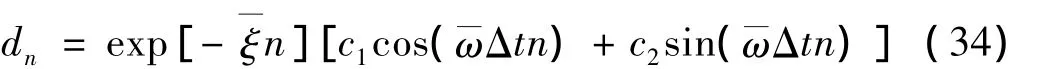
其中:

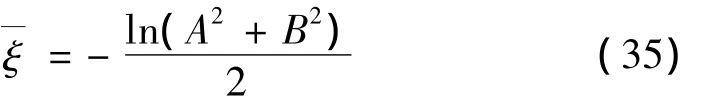
反映了算法对结构位移响应的阻尼作用。根据表2中n与β的关系，考虑n=2，β=0.52时，数值阻尼比随刚度变化系数μ的变化情况如图4所示，可见在给定条件下，当结构为刚度常量或硬化情况时，算法中引入了数值阻尼，而在结构刚度软化情况时，算法中并没有引入足够的算法阻尼。因此，为了使高阶单步法在结构刚度软化过程中仍具有一定的算法阻尼，需要进一步考虑关于算法数值阻尼的影响因素，为此，单独讨论结构刚度软化情况时，β取值的变化对算法数值阻尼的影响，在n=2，μ=0.8时，β取值变化对数值阻尼比的影响如图5所示，随着β取值的增大，系统的阻尼比有逐渐增大的趋势，因此对于结构刚度软化情况，通过适当增大β值，可以有效调整算法的数值阻尼。

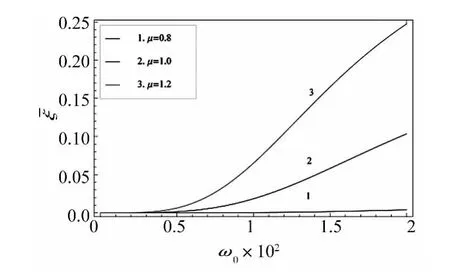
图4 n=2，β=0.52时刚度变化对数值阻尼比的影响Fig.4 Numerical damping ratio under different stiffness variation coefficients with n=2 and β=0.52

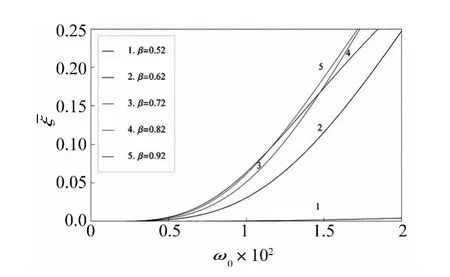
图5 n=2，μ=0.8时β变化对数值阻尼比的影响Fig.5 Numerical damping ratio under differentβ with n=2 and μ =0.8

3 系统阻尼对误差传递效应的影响

拟动力试验过程中，当我们使用高阶单步法做位移控制时，位移步之间存在误差的传递效应，一方面是由于试验过程中传感器的灵敏度为有限值，另一方面是由于计算机的计算精度为有限位数，都将导致试验的计算位移与反馈位移之间存在误差，拟动力试验过程需要对这些本身带有误差的数据进行不断的迭代运算，因此导致试验误差的累积，形成累积误差，对高阶单步法误差传递效应的研究，参考文献［5］中对算法误差传递效应的分析方法，引入下列变量:

dn:第n步精确数值计算位移;

den:第n步精确位移，包括之前步的位移误差;

dan:第n步实际位移，包括当前步与之前步的位移误差;

edn:第n步产生的位移误差。

它们之间存在如下的关系:

根据式(36)，对式(14)进行重写，则

令

得到算法的累积误差

其中:

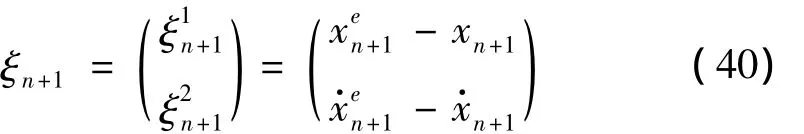
由于算法的累积误差与其积分步数有关，因此需要以确定的积分步数对算法的误差传递效应进行研究，参考文献［9－11］，采用两步累积误差迭代的方法对误差传递效应进行研究，并进一步化简式(39)，得到

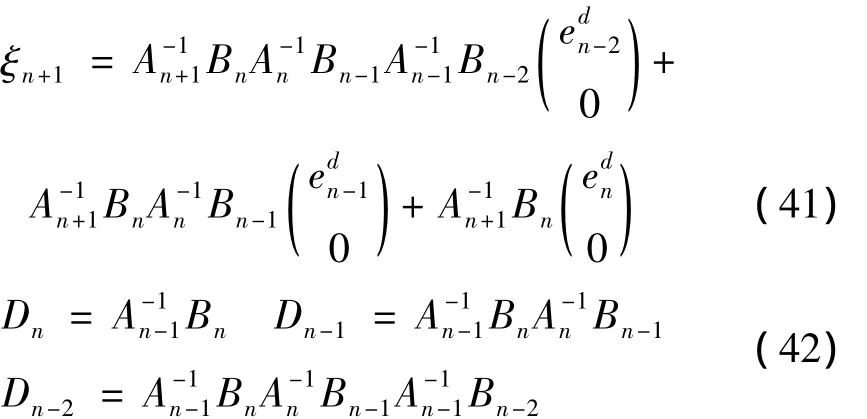
其中:Dn表示对当前第n+1步之前第n步误差的误差传递作用，Dn－1表示对当前第n+1步之前第n－1步误差的误差传递作用，Dn－2表示对当前第n+1步之前第n－2步误差的误差传递作用。

根据式(40)，当前第n+1步的位移累积误差为

为进一步研究算法对位移时程的误差传递效应，研究当 n=2，β =0.52 时，Dn－2、Dn－1与 Dn对其各自积分步中位移误差项的作用，在不同的刚度变化系数下，Dn－2、Dn－1与 Dn随系统频率的变化如图 6 所示。通过对图6中(a)、(b)和(c)的比较，发现当前积分时间步的累积误差对过去时间步的误差有明显的抑制作用，但抑制作用的强弱有明显的不同，Dn－2衰减最快，说明的误差抑制作用显著，Dn－1次之，Dn最差，说明过去的积分时间步距离当前步的时间越久，其对应的误差传递效应越弱，即当前积分时间步的累积误差效果主要取决于过去有限时间步的步数。同时，对比在不同刚度系数条件下算法的误差传递效应，发现在刚度软化过程中，其对应的误差传递效应比在刚度常量及硬化过程中的效应更强，而在刚度硬化情况下，其对应的误差传递效应较小。

前面已经证明，在拟动力试验过程中，我们可以通过调节β的取值，控制算法的数值阻尼，因此，通过改变β值可以实现对试验过程误差传递效应的控制，图7为考虑结构刚度变化系数为0.8的情况下，取不同的β值对 Dn－2、Dn－1和 Dn的影响，对比发现，在确定的结构频率点处，当β(大于0.5)的取值过小时，系统的误差传递效应较为明显，尤其是对Dn的影响较大，随着β取值的逐渐增大，算法的误差传递效应逐渐变小，同时，对于确定的 β 值，Dn－2、Dn－1和 Dn对应于不同结构频率表现出不同的误差传递效应，在系统频率较高时，由之前的讨论可知，系统的阻尼较大，因此，系统的误差传递效应明显，Dn－2、Dn－1能够较快地趋于零，Dn趋于某一较小的确定值(由β值决定)。上述结论是在刚度变化系数为0.8的情况下得到的，经过大量的数值计算，可以证明这个结论同样适用于刚度常量及硬化过程。

4 误差传递效应仿真实验

为进一步说明高阶单步法的误差传递效应对拟动力试验过程的影响，对单步积分算法进行数值实验仿真。数值实验采用的地震波为1940 EI Centro地震波，峰值加速度为2 g，为便于结果分析，取单自由度非线性系统，质量为40 000 kg，刚度108kN/m，忽略系统的物理阻尼，同时考虑引入误差对单步积分结果的影响，研究当b取0.9、1.0及1.1时，结构的位移时程响应和累积误差随系统刚度的变化情况。三种取值条件下系统对应的结构刚度变化系数分别为0.997 90、1.0和1.001 91，相应的分析结果如图8～10所示，其中(a)图为位移时程曲线(理论曲线与实际曲线)，(b)图为引入的随机误差，其幅值为0.12 mm，(c)图为累积误差曲线。对比图8～10中的(a)图即位移响应时程曲线，发现三种(刚度软化、刚度常量和刚度硬化)情况下，引入误差后结构的位移时程曲线(实际曲线)仍与理论曲线有较好的重叠，说明三种情况下对应的系统均有较强抗干扰能力，通过对三种情况下对应的系统累积误差分析，可以进一步得到上述的结论。同时，分析发现当结构刚度变化系数取值(0.997 90)小于1发生刚度软化情况时，对比其它两种情况，在系统的结构刚度较小情况下，系统的累积误差较大，并有逐渐变大的趋势，说明系统的误差传递效应较强，而在系统结构刚度常量及硬化过程中，系统的累积误差均得到有效的控制，误差被控制在一个稳定的范围内，并没有随积分步数的增多持续增大，误差传递效应较小。三种情况下对应的系统相位角Ω=ωΔt的变化如表3所示，在结构软化过程中，相位角的变化范围为1.0～0.418，逐渐变小，由之前讨论的关于刚度软化对系统数值阻尼及累积误差的影响可知，Ω较小(系统频率较小)时数值阻尼较小，误差传递效应较强，导致系统累积误差逐渐增大;另一方面，系统频率的变小使得系统相较于线性系统(图9)振动周期变长，有限时间里历经的循环次数变少(图8)。在系统结构刚度硬化过程中，系统相位角Ω的变化范围为1.0～3.14，逐渐增大，数值阻尼增大，误差传递效应变弱;同时，系统频率的增大导致系统相较于线性系统(图9)周期的缩短，因而在有限时间里系统历经的循环次数增多(图10)，循环次数的增多将导致系统累积误差的增大，在系统结构硬化过程中，由于大阻尼的存在能够很好的抑制系统误差的累积，使系统的误差累积效应较小(图10(c))。

图6 β =0.52时不同刚度变化系数对 Dn－2、Dn－1和 Dn的影响Fig.6 Dn－2，Dn－1 and Dn under different stiffness variation coefficients with β =0.52

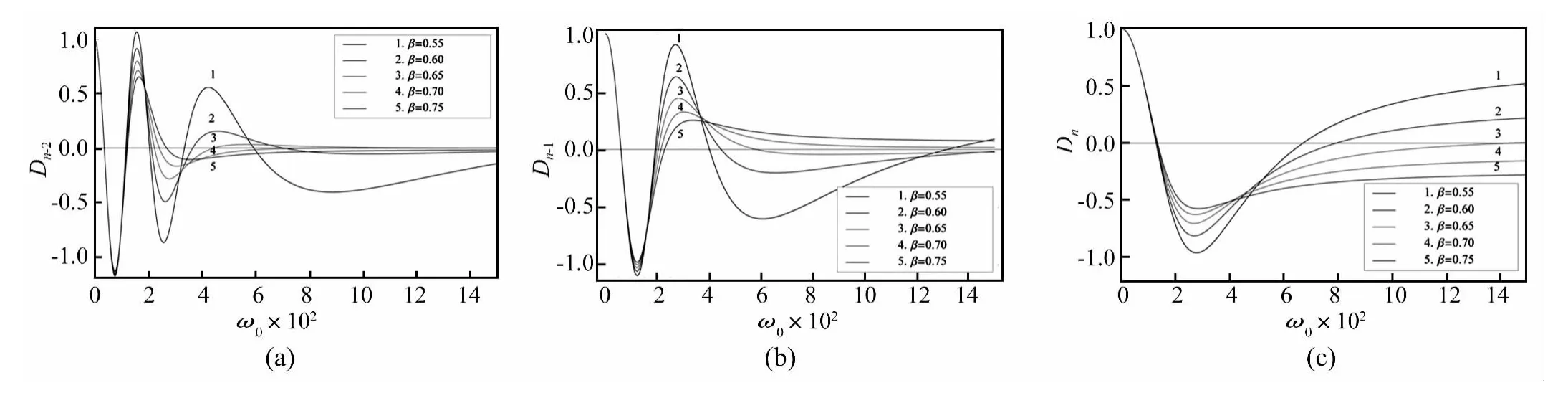
图 7 μ =0.8 时 β 变化对 Dn－2、Dn－1和 Dn的影响Fig.7 Dn－2，Dn－1 and Dn under differentβ with stiffness variation coefficientμ =0.8

图8 刚度软化时拟动力试验仿真Fig.8 Numerical simulation of pseudodynamic testing of consistent softening system

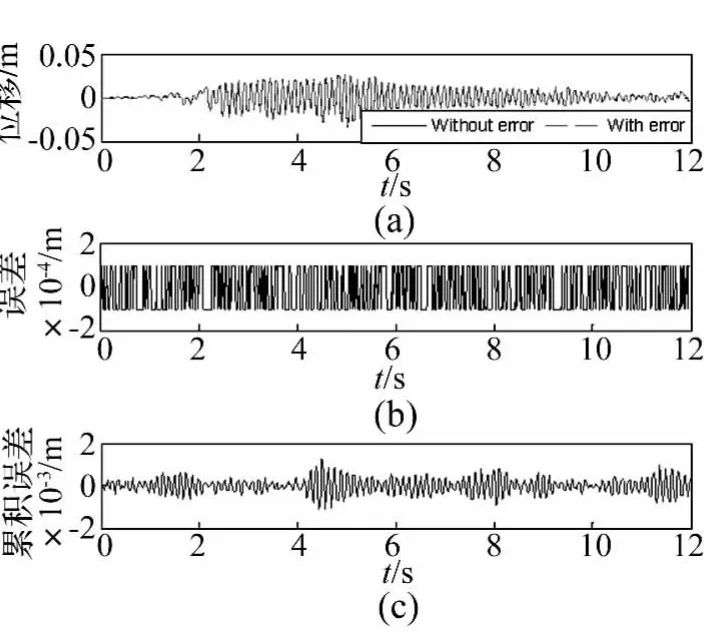
图9 刚度常量时拟动力试验仿真Fig.9 Numerical simulation of pseudodynamic testing of linear elastic system

图10 刚度硬化时拟动力试验仿真Fig.10 Numerical simulation of pseudodynamic testing of consistent hardening system

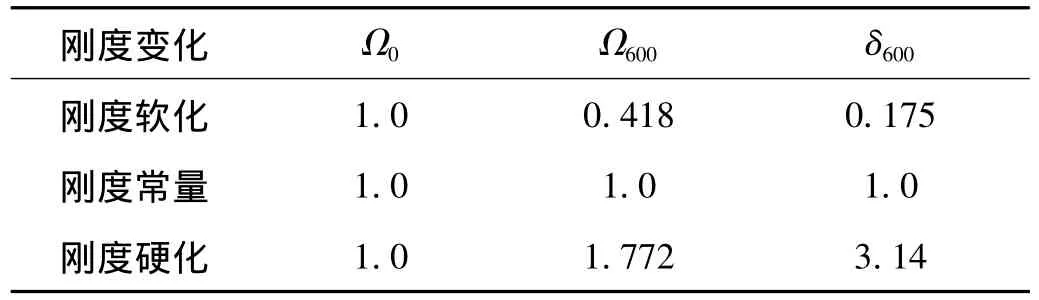
表3 i=0和600时对应的Ω1值Tab.3 Values ofΩ1 for i=0 and 600

表4 i=0和600时对应的ωi值Tab.4 Values ofωi for i=0 and 600

图11 刚度软化时β对系统累积误差的影响Fig.11 Influence on the cumulative error under differentβs for the consistent softening system

在系统结构刚度软化过程中，系统的频率从50 rad/s减小到20.9 rad/s(表4)，由图5，图7的理论分析结果可知，在系统的结构频率较小时，算法的数值阻尼较小，结果导致系统有较强的误差累积效应。为进一步研究系统结构刚度软化过程中β变化对系统累积误差的作用，讨论 β 取值分别为0.4，0.5，0.6 和0.7 情况下，系统的累积误差，结果如图11所示，在β取值0.4时，随着系统刚度的减小，系统累积误差有逐渐增大的趋势，导致系统失稳，在β取值0.5情况下，由于算法数值阻尼的增大(图5)，系统的累积误差得到有效控制，进一步增大β，系统的累积误差进一步减小，对比图11中(b)、(c)、(d)发现随着β取值的增大，系统的累积误差有减小的趋势，继续增大β(大于0.6)，算法对系统累积误差的影响已不明显，系统的累积误差趋于稳定的变化范围。

5 结论

本文对高阶单步法在非线性系统中的应用进行了研究，讨论了刚度变化系数μ和参数β对系统的稳定性及其数值阻尼的影响，证明在系统软化过程中β取值过小将导致系统不稳定，而通过适当增大β值可以满足系统在结构刚度软化过程中的稳定性;同时，在系统刚度软化过程中系统的数值阻尼较小，这不利于系统对高阶模态响应的抑制作用，而通过增大β值能够使系统即使在刚度软化的过程中仍具有较好的阻尼特性。系统的误差传递效应对系统结构刚度变化系数μ和参数β的取值比较敏感，在系统结构刚度软化过程中，系统的误差传递效应比较强烈，导致系统的累积误差增大，通过适当调节β的取值可以有效减少系统的累积误差，削弱系统的误差传递效应。

［1］Shing P B，Mahin S A.Cumulative experimental errors in pseudodynamic tests［J］.Earthquake Engineering and Structural Dynamics，1987，15:409 －424.

［2］Shing P B，Mahin SA.Elimination of spurious higher-mode response in pseudodynamic tests ［J］. Earthquake Engineering and Structural Dynamics，1987，15:425－445.

［3］王焕定，张永山，王 伟，等.非线性结构时程分析的高阶单步法［J］.地震工程与工程振动，1996，16(3):48－54.WANG Huan-ding，ZHANG Yong-shan，WANG Wei，et al.The high order one step－βmethod for seismic response analysis of non-linear structures［J］.Earthquake Engineering and Engineering Vibration，1996，16(3):48－54.

［4］崔雪娜，王焕定.刚度解析表达时高阶单步法的研究［J］.地震工程与工程振动，2006，26(4):63－67.CUI Xue-na，WANG Huan-ding.Research on a high order single step method for analytic expression of stiffness［J］.Earthquake Engineering and Engineering Vibration，2006，26(4):63－67.

［5］Chang S Y.Nonlinear error propagation analysis for explicit pseudodynamic algorithm ［J］. Journal of Earthquake Mechanics，2003，129(8):841 －850.

［6］Chang SY.Performance of HHT－αmethod for the solution of nonlinear systems［J］.International Journal of Structural Stability and Dynamics，2008，8(2):321－337.

［7］Chang S Y.Numerical characteristics of explicit method for nonlinear systems［J］.Journal of Earthquake Engineering，2007，11(5):694－711.

［8］邱法维，钱稼茹，陈志鹏.结构抗震实验方法［M］.北京:科学出版社，2000.

［9］Chang SY.Nonlinear performance of explicit pseudodynamic algorithm ［J］.Journal of Earthquake Engineering，2010，14(2):211－230.

［10］Chang S Y.Error propagation of HHT － α method for pseudodynamic tests ［J］. Journal of Earthquake Engineering，2005，9(2):223－246.

［11］Chang SY，Sung Y C.Analytical exploration ofγ－method explicit method for pseudodynamic testing of nonlinear system［J］.Earthquake Engineering and Engineering Vibration，2005，4(1):117－127.