基于欧拉单元的水下气泡高效数值仿真算法研究

苏怡然，唐文勇，郑绍文，李德聪

(1.上海交通大学 海洋工程国家重点实验室，上海 200240;2.中国舰船研究设计中心，武汉 430064)

在实际工程中，气泡脉动引发冲击作用的实例有很多:如水下爆炸气态产物对船体结构造成冲击、螺旋桨工作时产生的毫米量级的空化气泡对螺旋桨的剥蚀，以及超声辐照产生的微米量级气泡对微生物的冲击作用等。当气泡距离结构足够近时，其脉动过程往往伴随着高速水射流［1］。水射流产生后会穿透气泡并对附近结构造成冲击，此过程为气泡破坏效应的主要机理之一。

关于水下气泡的运动特性，早期研究［1－2］主要基于一些理想假设，如气泡呈球状变化等。近年来，随着计算机技术的发展，气泡非球状演化过程的数值模拟已成为可能。边界积分方法假设流场无粘、无旋且不可压缩，使用低维模型模拟高维空间，有效减小了计算量，在模拟水下爆炸气泡射流现象中已有许多成功的应用［3－7］。但上述假设限制了边界积分法的应用范围:如螺旋桨空泡或超声激发的气泡，气泡尺寸往往较小，此时粘性对气泡脉动的影响显著;再如水下爆炸气泡回弹阶段，激波引起的能量耗散将对气泡演化规律造成影响，在该过程的数值模拟中流体可压缩性将不可忽略;此外，在射流穿透气泡后，气泡表面速度势变为多值函数，计算将被终止，需引入环状气泡模型才能对该气泡进行模拟。因此，使用更具一般性的Navier-Stokes方程(以下简称NS方程)模拟气泡脉动具有实际意义。

针对水下气泡的非球状脉动现象，Popinet等［8］使用MAC法成功模拟了毫米量级气泡的射流过程，Hao等［9］将该法拓展到三维直角坐标系中，Johnsen、McKee等［10－11］实现了可压缩流体中射流现象的数值模拟，张凌新等［14］使用VOF法模拟了水下爆炸气泡的溃灭现象。这些方法均需要将流体边界取在远离气泡的位置，导致计算效率低下，尤其对于一些高强度气泡，巨大的计算耗时将使数值模拟缺乏实用性。

本文在MAC法［13］基础上提出一种适用于模拟气泡脉动问题的近场压力边界条件，通过合理减小计算区域，提高了MAC法的计算效率，解决了高强度气泡数值模拟中计算耗时较大的问题。通过引进Popinet［8］和Hirt［12］等对自由液面的处理方法，保证了自由液面边界条件的计算精度和数值稳定。

1 数学模型

1.1 控制方程

对于水下气泡首次周期内的脉动问题，使用轴对称不可压缩NS方程进行描述:

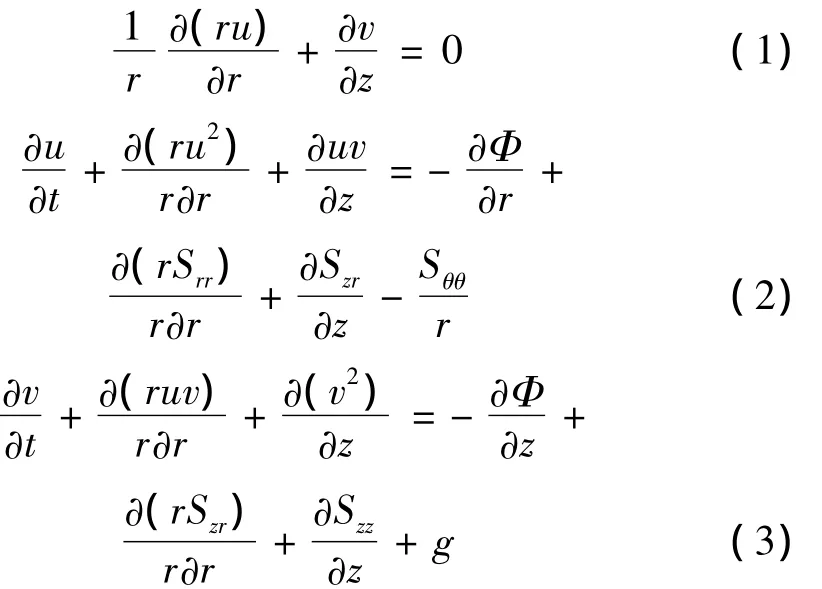
其中:Φ=p/ρ代表压力，ρ为液体密度，g为重力加速度，γ为运动粘性系数，剪应力分量计算方法如下:

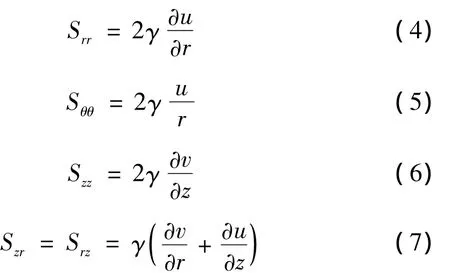
轴对称模型如图1所示，方程需满足的边界条件为:

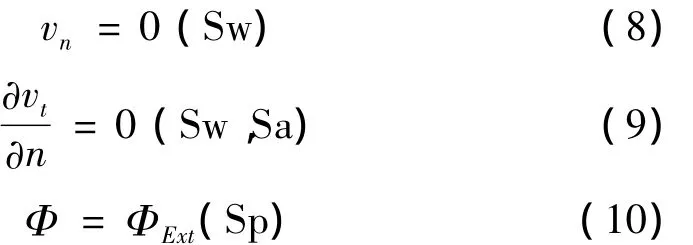
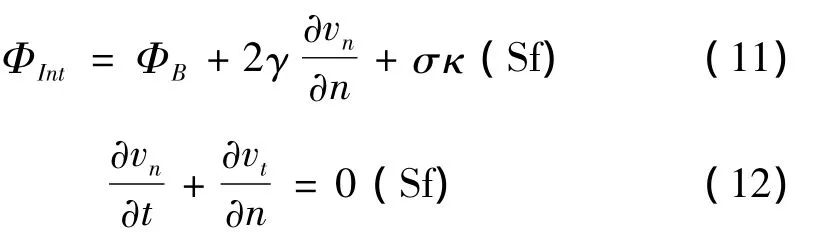
对欧拉域外围边界Sp使用压力边界条件，边界上的压力值由远端流场确定。在求解远端压力分布时，本文将脉动气泡假想为空间源汇，使用势流理论计算远场压力，详见本文第2章。

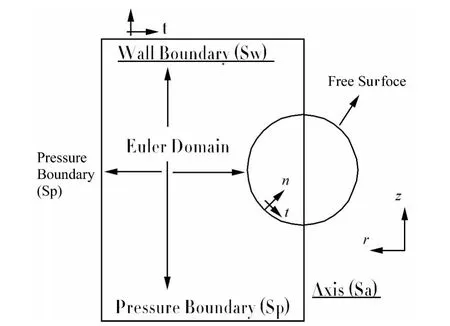
图1 水下气泡数值模型Fig.1 Numerical model for the simulation of underwater bubbles

1.2 离散方法

使用交错网格对NS方程进行离散，压力节点和速度节点分别位于网格中心和网格边长中点。NS方程在空间上采用中心差分离散格式，在时间上使用一阶隐式欧拉法进行离散。

使用预测－校正法解决不可压缩流动的压力－速度耦合问题［15－16］:在每个时间步内，首先忽略压力梯度项，通过动量方程求出预测速度，进而得到压力泊松方程，使用逐次超松弛迭代法对该方程进行求解，最后用压力梯度对预测速度进行校正。

在处理自由液面问题时，本文采用改进MAC法的思想，通过标记点追踪自由液面运动，实现了对自由液面的精确捕捉。首先在自由液面上布置一串具有先后顺序的无质量标记点，并在每个时步内使标记点跟随流场运动，从而实现自由液面形状和位置的追踪。标记点的运动速度由四个相邻节点速度进行双线性插值得出。在计算过程中，需要不断进行标记点位置的重分配，以保证标记点沿液面均匀分布，从而降低计算误差。自由液面将欧拉网格划分为流体网格、液面网格和空网格三类，其中空网格不参与计算。

液面法向边界条件见式(11)，式中σ为表面张力系数，κ为液面曲率，ΦInt为自由液面附近流场压力，ΦB为气泡内压力。传统处理方法简单地认为边界单元压力等于液面压力，这样处理在边界法向压力梯度较小时可满足精度要求，但对于本文研究的高压力梯度问题，会造成计算误差与数值波动。为使计算误差得到控制，采用Hirt等［14］提出的边界单元压力计算方法:认为压力在边界附近呈线性分布，边界单元压力由相邻流体单元压力与液面压力插值得到。

液面切向边界条件见式(12)。根据Popinet等［8］提出的方法实现该条件，即认为自由液面运动速度是由周边流体网格处流速和空网格虚拟速度插值得到，通过人为指定虚拟速度的大小，可使流场满足切向边界条件。于是，该问题转化为条件极值问题:

2 近场压力边界

对无穷流域问题进行数值模拟时，普遍需要通过较大的模型范围来逼近无穷远边界，计算效率较低。尤其对于高强度气泡，脉动过程中最大半径可达初始半径的30余倍，巨大的计算量将使数值模拟失去实用性。本文根据Best等［17］得到的规律，提出一种由近场压力边界描述无穷流域的数值算法，有效缩小了模型尺寸，提高了计算效率。

2.1 边界压力算法

Best等［17］提出，距气泡一定距离之外的流场可近似看作发散状。因此，将气泡假想为空间点源(汇)，可认为远端流场由该点源(汇)激发。设V为气泡体积，Q为点源(汇)强度，r为空间点到气泡中心的距离，远端流场速度势为:

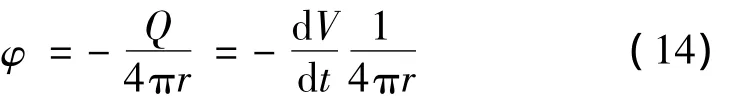
当气泡靠近壁面时，流场会受到镜面效应影响。此时，需在气泡镜像点处施加一个等强度的点源(汇)。设r1和r2分别表示空间点至气泡中心和镜像位置的距离，远端流场速度势为:

在忽略远端粘性影响后，流场压力可由伯努利方程求出。设Φ∞为无穷远处压力(静水压)，近场边界压力ΦBC可由式(16)求出:

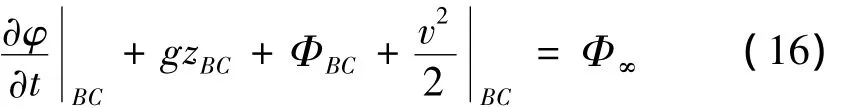
将ΦBC作为近场边界的压力值，即可减小数值模拟所需的模型尺寸。

2.2 稳定性证明

首先，对源强度施加小量误差δQ，该误差引起的近场边界压力误差为:

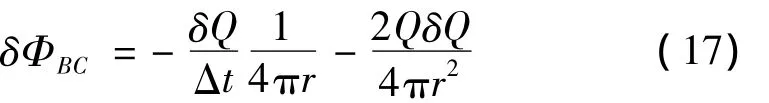
由于时间步长Δt足够小，式中第二项可以忽略。设R与·R·分别为气泡等效半径R对时间的一阶和二阶导数，则有 δ(·R·)≫ δ (R·)≫ δ(R)。根据Rayleigh-Plesset方程的积分形式:

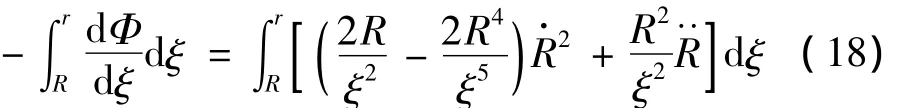
忽略无穷小量后可得:

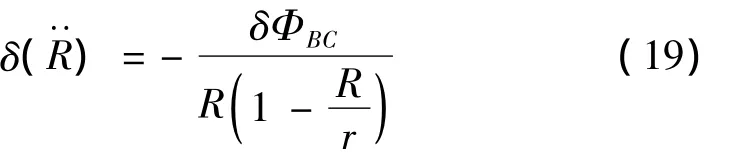
忽略无穷小量后可得:

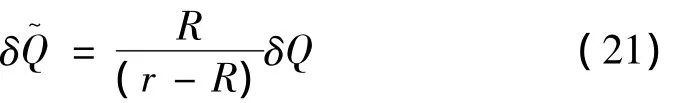
可见，当近场边界距气泡中心距离大于两倍气泡最大半径时，近场压力边界条件已具有稳定性。

2.3 边界合理性判断与数值震荡抑制

当标记点移动至新网格时，其速度将由新的一组节点速度插值得到，这会引起标记点速度的微幅波动。由于时间步长很短，该波动对于气泡尺寸的影响可以忽略，但却会使产生较大误差，从而直接影响近场边界压力的准确性。若不加控制，还易引发数值震荡，导致计算失败。

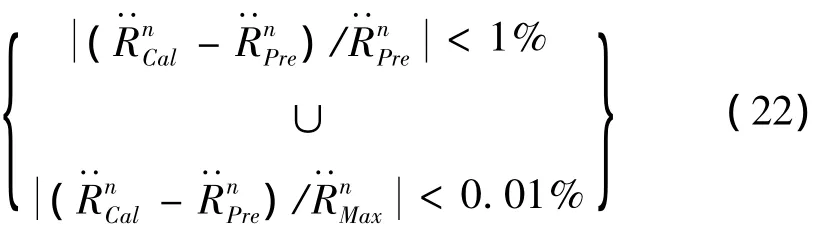
3 可靠性验证

气泡的球状演化规律由 Rayleigh-Plesset方程给出:

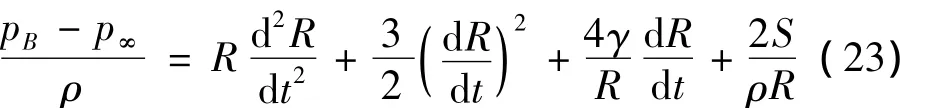
其中:R为气泡等效半径，γ为运动粘性系数，S为表面张力系数，p∞为静水压力，pB为气泡压力。气体状态方程为:

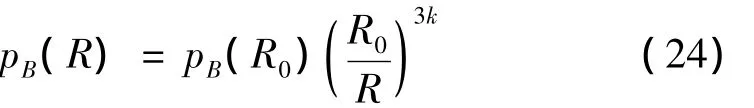
式中:k为气体绝热指数，取1.4。

从本质上讲，Rayleigh-Plesset方程是NS方程在理想条件下的简化形式，因此，算法可靠性的最基本要求即为可逼近Rayleigh-Plesset经典解。对忽略重力作用与壁面作用的气泡脉动过程进行数值模拟，考虑不同强度的气泡(设气泡强度系数为其压力峰值与环境压力的比值，这里取 50，100，150，200)，模型参数见表 1，计算结果如图2所示。在强度系数为50时，气泡半径误差为0.2%;随着强度增高，半径误差略微变大，这是因为在模型尺寸不变的情况下，随着气泡体积变大，近场边界距气泡距离不断减小。计算结果表明，各项误差均在可接受范围内，其中半径误差小于1%，脉动周期误差约为0.5% ～0.6%。

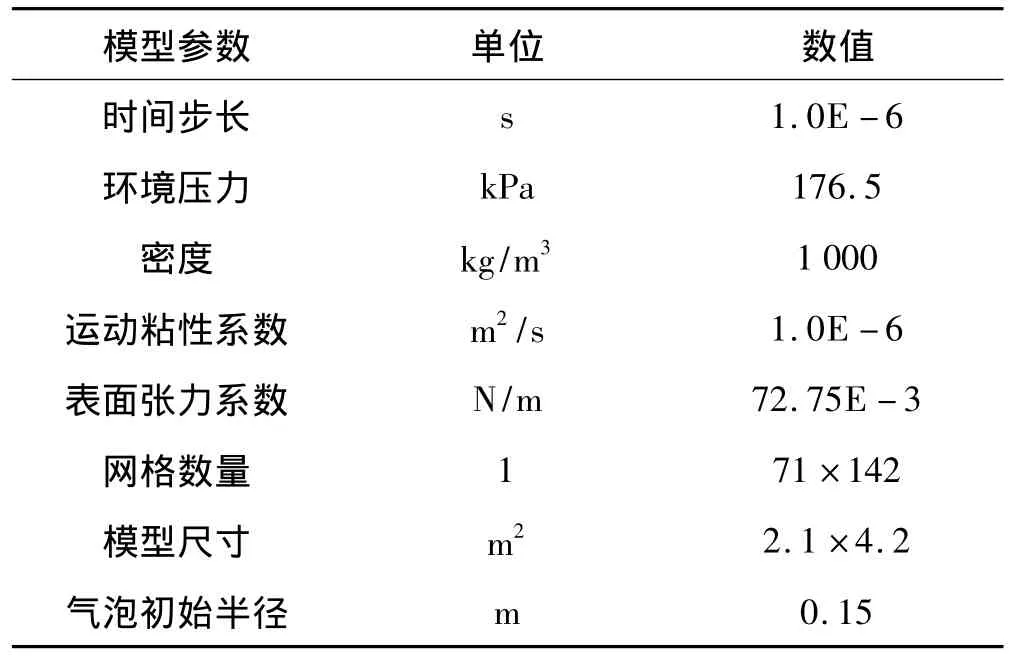
表1 数值模拟主要参数Tab.1 Parameters of numerical model

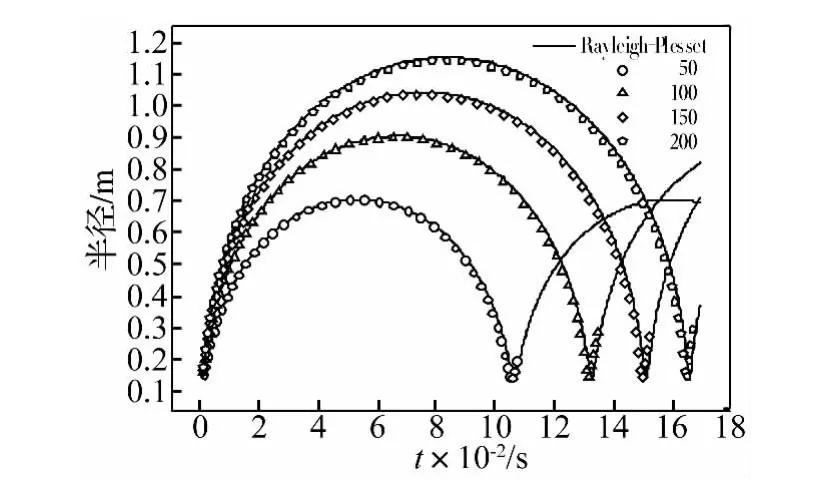
图2 近场边界方法与R－P方程计算结果对比Fig.2 Result comparisons between the near-field boundary method and the R-P equation

无穷流域问题数值模拟的传统方法需使用较大的模型范围，且模型边界条件设为恒定静水压力。为验证本文所述边界条件在提高计算效率、降低计算误差中的效果，表2将两种边界条件的误差进行了对比。对于不同模型尺寸，恒压边界均会产生更大的误差，尤其是脉动周期误差。随着模型尺寸的增大，两种算法的误差均有所减小，其中近场压力边界的误差维持在0.5%左右，而恒压边界的误差则从36%快速下降，但即使模型范围达到10倍气泡半径，恒压边界误差依然大于近场压力边界误差。这说明本文所述边界压力算法在提高计算效率的同时也降低了计算误差。

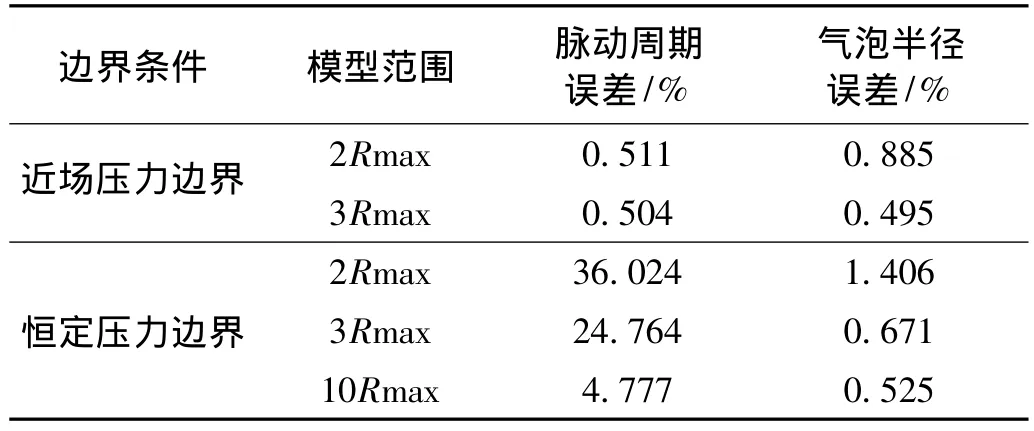
表2 近场边界与恒压边界误差比较Tab.1 Error comparison between near-field boundary and constant pressure boundary

然而，上述模型中自由液面均未发生变形。为验证算法处理液面变形问题的可靠性，本文对重力作用下的气泡脉动过程进行数值模拟，并与实验数据进行了对比。Shima等［18］采用脉冲放电的方法产生水下气泡，并提出由气泡平衡半径Re来确定气泡压力:

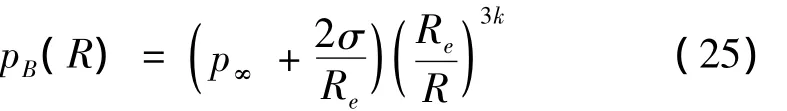
对于该实验涉及的气泡尺寸，流体粘性效应影响可以忽略，但由于粘性作用显著的微米量级气泡的脉动实验难以进行，所以这里仅将上述实验数据同数值仿真结果进行对比，作为证明算法可靠性的依据，计算结果如图3所示。在首次脉动周期内，数值模拟结果与实验数据吻合良好，气泡半径平均误差为气泡最大半径的3.91%，脉动周期误差为2.68%;当气泡进入回弹阶段时，数值模拟得到的气泡等效半径明显大于实验结果。这是因为在回弹阶段，多种物理过程产生的能量耗散效应逐渐显著，如气泡界面上热交换、可压缩流体激波等。

Klaseboer等［4］在实验水池中进行了不同装药量的爆炸实验，并进行高速摄影，图4给出了爆炸气泡脉动过程与数值模拟结果的对比，两者在趋势上吻合较好。从数值模拟结果可以看出，在溃灭阶段，受重力的作用，射流产生于气泡底端并逐渐发展至穿透气泡，射流方向与重力方向相反。实验中监测了爆炸气泡附近压力场随时间的变化，由近到远三个监测点分别记为P1、P3、P5。图5对比了三个监测点压力的实验数据和数值计算结果。可以看出，两者趋势一致，误差保持在15%以内。产生该误差的主要原因是试验水池边界和数值模型边界之间的差异。数值模拟中没有考虑池壁、水面等边界影响。此外，由于算法没有考虑流体压缩性，所以不同监测点同时达到压力峰值，而非试验中先后达到峰值。

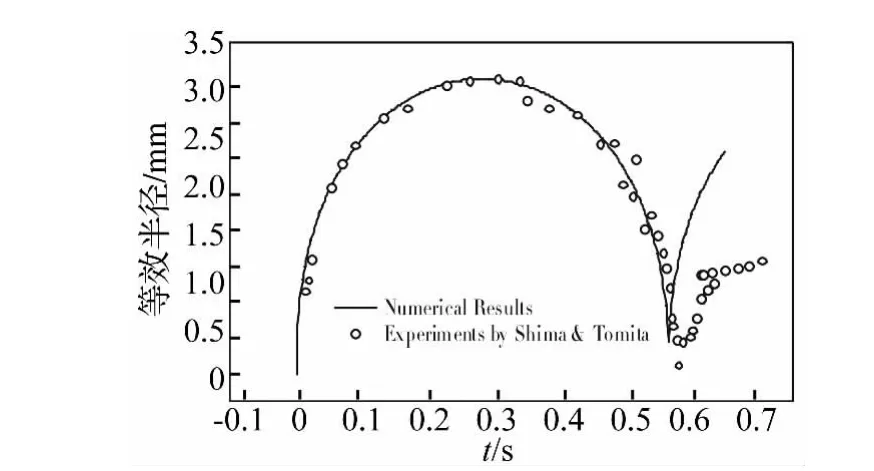
图3 重力作用下气泡等效半径随时间变化Fig.3 Time history of bubble equivalent radius under the influence of gravity

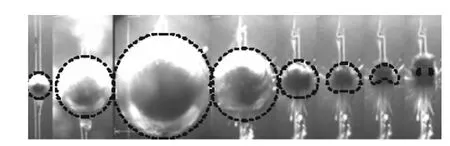
图4 水下爆炸气泡脉动过程(虚线为数值模拟结果)Fig.4 Pulsation of underwater explosive bubbles(The dash line represents numerical results)

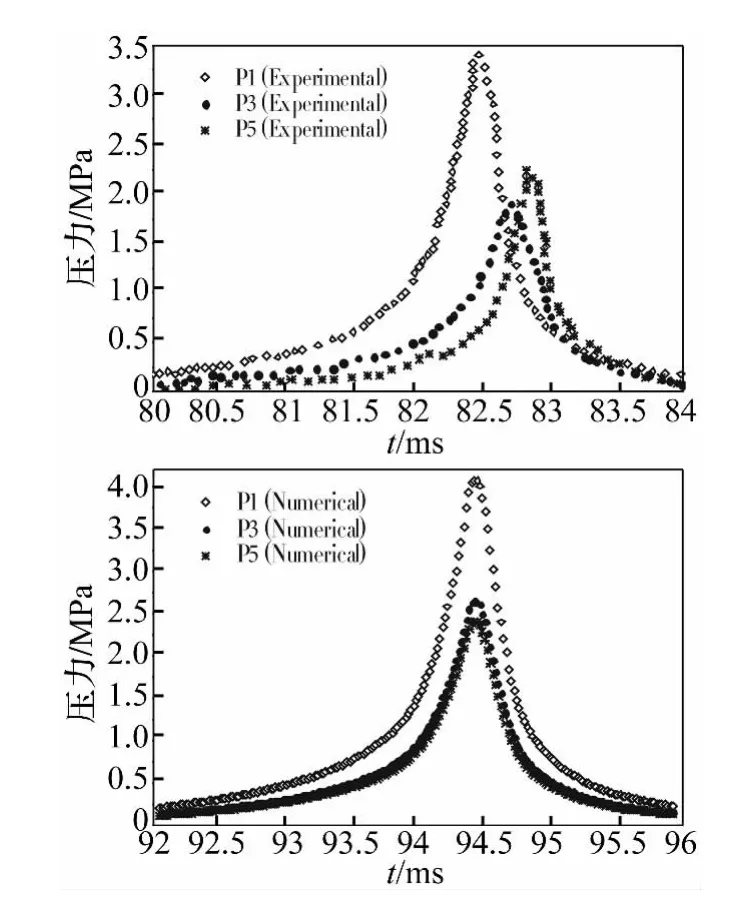
图5 爆炸气泡附近压力随时间变化Fig.5 Time evolution of the pressure near explosive bubble

4 近壁气泡脉动过程分析

近壁气泡脉动过程往往伴随着射流现象，由于国内外公开的相关实验结果多为高速摄影，定量分析较为匮乏，故本文仅对典型近壁气泡脉动过程进行定性分析。Tomita等［19］使用脉冲放电的方法制造出近壁气泡，并进行高速摄影，如图6(a)所示，图6(b)为该过程的数值模拟计算结果。数值模型中，气泡位于7.5 m水深，强度系数取50，初始半径为0.15 m，气泡距壁0.7 m。

在膨胀阶段，气泡始终保持近似球形，并被固壁略微排斥，膨胀阶段停止于约0.5倍脉动周期;随后进入溃灭阶段，该阶段内气泡受固壁的强烈吸引而产生大幅位移和变形，在溃灭阶段尾期，射流形成于气泡远离固壁端;在124 ms时刻射流击穿气泡，使气泡变为环状。

射流形成时刻流线图与压力云图的计算结果如图7所示。此时，气泡压力大于静水压力，气泡处于减速收缩阶段，且射流后方存在局部高压区域;流场边界处流动近似发散状，这与Best［17］提出的流速规律是相吻合的。

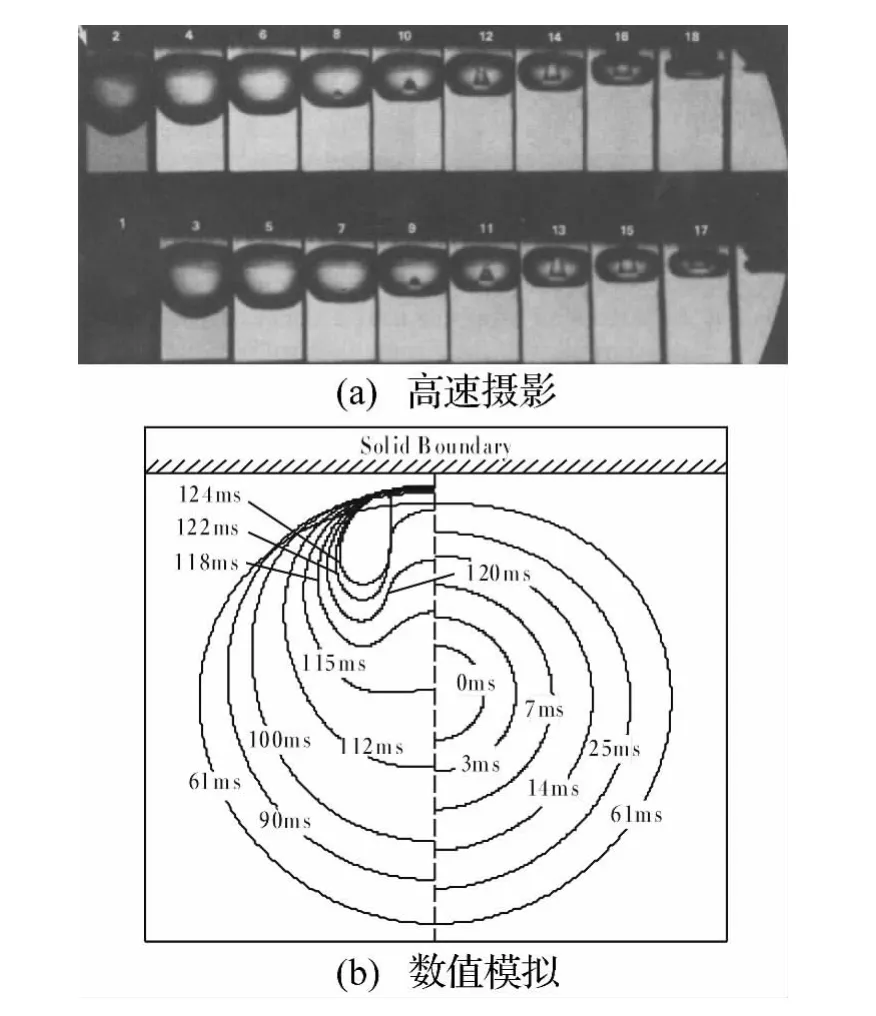
图6 近壁气泡脉动过程Fig.6 Bubble pulsation in the vicinity of a rigid boundary

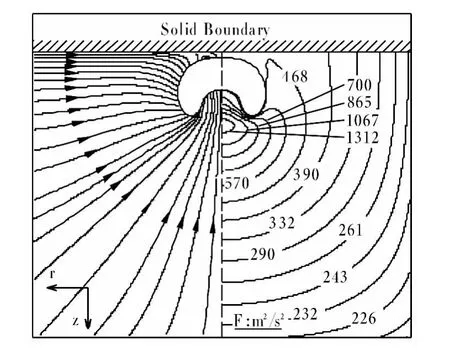
图7 射流形成时刻流线图与压力云图Fig.7 Streamlines and pressure profiles at jet formation

5 结论

本文基于NS方程，提出一种近场压力边界算法，有效提高了计算效率。该方法适用于水下爆炸气泡脉动、螺旋桨空泡溃灭等多种过程的数值模拟和相应射流冲击载荷的预报。本文主要结论如下:

(1)本文所述近场压力边界允许通过较小区域的流体模型模拟无穷流域问题，大幅提高了计算效率;

(2)MAC方法适于追踪具有较大曲率的自由液面，允许人为的指定自由液面拓扑形状的改变，在水下气泡非球状脉动过程的模拟中表现出色;

(3)本文旨在阐明近场压力边界，所以文中主要模拟了气泡首次脉动周期内的近似不可压过程，关于气泡回弹时流体压缩效应和液面热交换作用的影响有待进一步研究。

［1］Blake J R，Gibson D C.Cavitation bubbles near boundaries［J］.Annual Review of Fluid Mechanics，1987，19(1):99－123.

［2］Plesset M S，Prosperetti A.Bubble dynamics and cavitation［J］.Annual Review of Fluid Mechanics，1977，9(1):145－185.

［3］Zhang Y L，Yeo K S，Khoo B C，et al.3D jet impact and toroidal bubbles［J］.Journal of Computational Physics，2001，166(2):336－360.

［4］Klaseboer E，Hung K C，Wang C，et al.Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure［J］.Journal of Fluid Mechanics，2005，537:387－413.

［5］ Zhang A M，Yao X L，Yu X B.The dynamics of threedimensional underwater explosion bubble［J］.Journal of Sound and Vibration，2008，311(4):1196 －1212.

［6］张阿漫，姚熊亮.水下爆炸气泡与海底相互作用研究［J］.振动与冲击，2008，27(3):92 －98.ZHANG A-man， YAO Xiong-liang. Interaction between underwater explosion bubble and seabed［J］.Journal of Vibration and Shock，2008，27(3):92－98.

［7］宗 智，何 亮，张恩国.水中结构物附近三维爆炸气泡的数值模拟［J］.水动力学研究与进展 A辑，2007，22(5):592－602.ZONG Zhi， HE Liang， ZHANG En-guo. Numerical simulation of a three-dimensional underwater explosion bubble near a structure［J］.Journal of Hydrodynamics Ser A，2007，22(5):592－602.

［8］ Popinet S，Zaleski S.Bubble collapse near a solid boundary:a numerical study of the influence of viscosity［J］.Journal of Fluid Mechanics，2002，464:137 －163.

［9］ Hao Y，Prosperetti A.A numerical method for threedimensional gas liquid flow computations［J］.Journal of Computational Physics，2004，196(1):126 －144.

［10］ Johnsen E， Colonius T. Numerical simulations of nonspherical bubble collapse［J］.Journal of Fluid Mechanics，2009，629:231 －262.

［11］ McKee S，Tome M F，Ferreira V G，et al.The MACmethod［J］.Computers＆ Fluids，2008，37(8):907－930.

［12］ Nichols B D，Hirt C W.Improved free surface boundary conditions for numerical incompressible-flow calculations［J］.Journal of Computational Physics，1971，8(3):434 －448.

［13］Hawker N A，Ventikos Y.Interaction of a strong shockwave with a gas bubble in a liquid medium:A numerical study［J］.Journal of Fluid Mechanics，2012，701:59 －97.

［14］张凌新，尹 琴，邵雪明.水中气泡溃灭的理论与数值研究［J］.水动力学研究与进展 A辑，2012，27(1):68－73.ZHANG Ling-xin，YIN Qin，SHAO Xue-ming.Theoretical and numerical studies on the bubble collapse in water［J］.Chinese Journal of Hydrodynamics Ser.A，2012，27(1):68－73.

［15］ Griffith B E.An accurate and efficient method for the incompressible Navier Stokes equations using the projection method as a preconditioner［J］.Journal of Computational Physics，2009，228:7565－7595.

［16］ Brown D L，Cortez R，Minion M L.Accurate projection methods for the incompressible Navier Stokes equations［J］.Journal of Computational Physics，2001，168(2):464－499.

［17］ Best J P.The dynamics of underwater explosions［D］.PhD dissertation. The University of Wollongong， New South Wales，1991.

［18］ Shima A，Tomita Y，Sendai.The behavior of a spherical bubble near a solid wall in a compressible liquid［J］.Ingenieur-Archiv，1981，51:243－255.

［19］Tomita Y，Shima A.High-speed photographic observations of laser-induced cavitation bubbles in water［J］.Acustica，1990，71(3):161－171.