磁悬浮轴承H∞鲁棒控制策略研究

龙亚文，谢振宇，徐 欣

主动磁悬浮轴承是利用可控电磁力将转子稳定悬浮的一种新型支撑装置，与传统轴承相比，具有无接触、无磨损、无需润滑、精度高和刚度阻尼可调等优点。可广泛应用于航空航天、交通、能源、超高速精密加工和机器人等领域［1］。

磁悬浮轴承的控制策略对系统的动静态性能有重要影响。对此，国内外许多学者从不同方面进行了研究。童水光等［2］利用电磁阻尼器来抑制转子的振动;谢振宇等［3］利用金属橡胶环—磁悬浮轴承组合支撑来提高系统阻尼，达到吸振的目的;张德魁等［4］采用LMS(Least Mean Square)控制算法对磁悬浮磨床电主轴系统的同步振动进行抑制，实验结果表明此控制策略能明显提高系统性能;段广仁等［5－6］在磁悬浮飞轮储能系统中采用鲁棒动态补偿控制，其设计的一阶参数化动态补偿器能明显抑制系统扰动，并使控制代价最小，减少系统能量损耗;Beals等［7］提出一种自适应力平衡(AFB)补偿控制策略，解决磁悬浮轴承中周期性振动问题;Tamisier等［8］提出一种前馈力补偿控制策略，根据不同转速计算不平衡补偿量，得到补偿信号;Kai等［9］提出一种自适应自动对心控制策略，能在线实时补偿系统的不平衡。

根据转子动力学知识，柔性转子系统在越过各阶临界转速时，转子振幅较大，容易与轴承碰撞;而当系统转速远离各阶临界转速时，转子振幅相对较低。为了有效抑制转子在各阶临界转速附近运行时的振动，同时不增加控制策略的复杂性，本文提出根据转子在固有频率处的振幅选择加权函数的方法，在磁悬浮轴承柔性转子系统试验台上，通过理论计算得到系统的不确定性和固有频率处的不平衡响应，通过仿真分析和高速旋转试验研究了混合灵敏度H∞控制策略对柔性转子系统动态性能的影响，并与PID控制策略进行了对比。

1 系统数学模型

1.1 系统工作原理

磁悬浮系统部分包括:传感器、控制器、功率放大器、电磁铁和转子。磁悬浮系统工作原理为:转子平衡参考位置假设为 x0(本实验台平衡气隙 x0=0.25 mm)，传感器检测位置信号为x，将两个信号差值输入控制器，根据控制策略进行运算，输出控制电压信号到功率放大器，最后输出差动电流控制电磁铁上、下线圈的电磁力，将转子拉回至平衡位置x0处。

1.2 系统数学模型

图1为系统转子受力示意图，参数含义见表1。

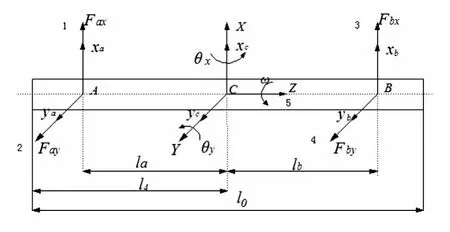
图1 转子受力示意图Fig.1 the rotor force diagram

表1 主要机械尺寸表Tab.1 Diagram of main mechanical size

转子质心处径向各自由度的运动方程可表示为:

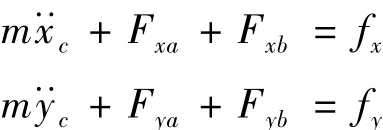
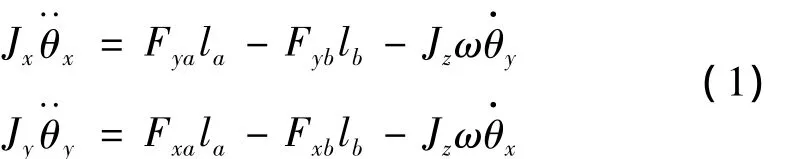
其中:fx，fy分别为 x，y 正方向的干扰力，Jx，Jy，Jz分别为转子绕x，y，z轴的转动惯。质心处位移为:

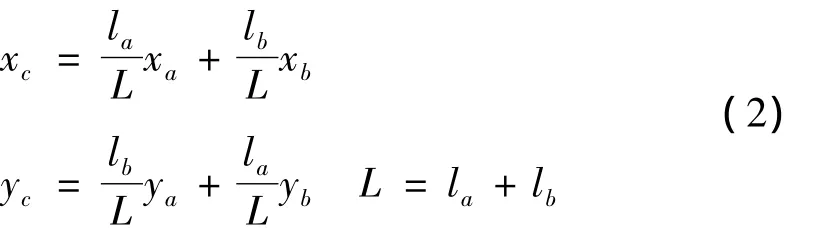
转子在xz、yz平面内的转角为:

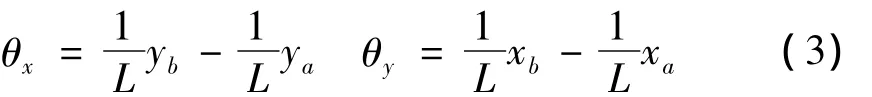
转子在轴承支撑平衡位置处的线性化电磁力为:

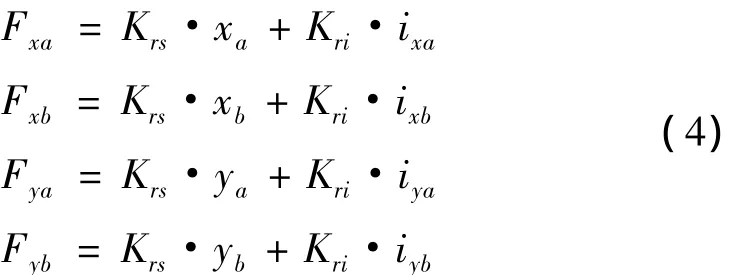
其中:Krs=－3.2×105N/m，Kri=32 N/A分别为径向位移刚度系数和径向电流刚度系数。

取状态向量X1=［xa，xb，ya，yb，

取控制向量 U1= ［ixa，ixb，iya，iyb］T

取输出向量 Y1= ［xa，xb，ya，yb］T

将式(2)、(3)、(4)代入式(1)中且令外干扰fx=fy=0，可得径向自由度的数学模型如式(5)所示。

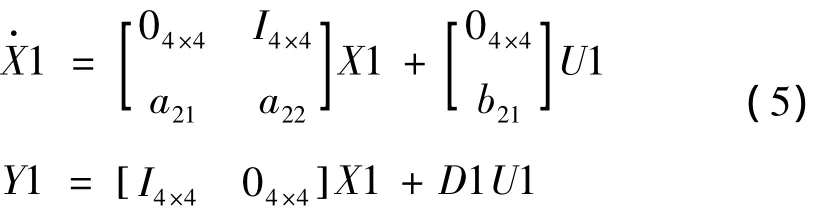
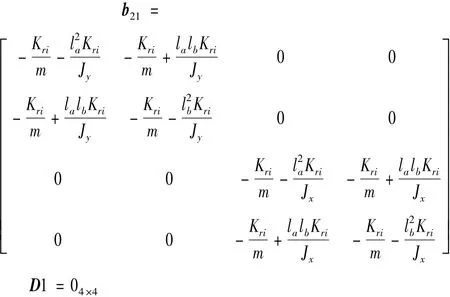
其中:参数矩阵 a21，a22，b21，D1 分别为:

转子质心处轴向运动微分方程可表示为:

轴向电磁合力

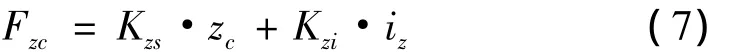
其中:Kzs= －1.2×105N/m 和 Kzi=12.13 N/A 分 别为轴向位移刚度系数和轴向电流刚度系数。

取控制变量 U2=iz

取输出变量 Y2=zc

令外干扰fz=0，则轴向自由度的数学模型可表示为:

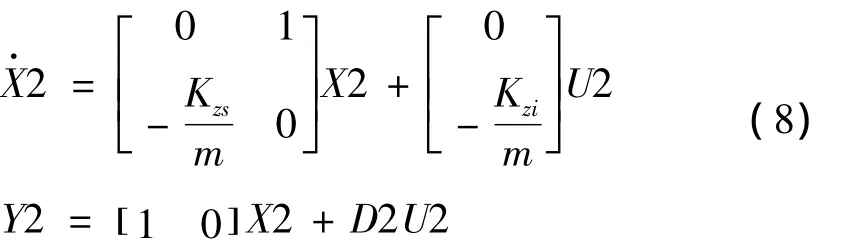
其中D2=0

综合上述径向和轴向数学模型，忽略上述参数矩阵中非对角元项(即忽略惯性耦合和陀螺耦合项)，得各自由度被控对象标称传递函数分别为:第1、2自由度

第3、4自由度

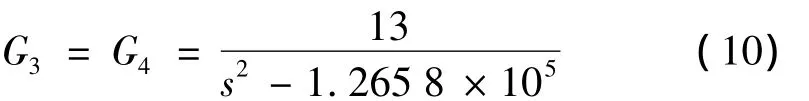
第5自由度

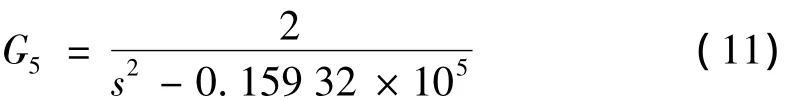
当系统近似为线性系统时，转子各个自由度的振动相似，故可通过分析其中某个自由度的振动获得转子的整体振动情况［3］。本文主要以径向第1自由度为例进行分析，其余自由度类似。

2 控制器设计

2.1 混合灵敏度H∞控制

以径向第1自由度为例，图2是该自由度的控制原理框图。

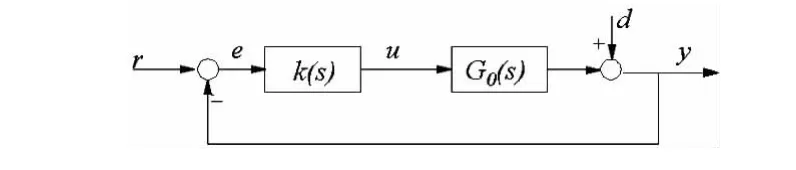
图2 控制系统原理框图Fig 2 principle of control system

图中r为参考输入，e为跟踪误差，u为控制输出，d为干扰输入，y为系统输出，k(s)为控制器，G0(s)为受控对象，则灵敏度函数S(s)，补灵敏度函数T(s)和函数R(s)定义分别为:

S(s)是系统干扰d到输出y的闭环传递函数矩阵，其增益表示闭环系统对低频干扰的抑制能力。

T(s)是参考输入r到y的传递函数矩阵，其增益表示对系统的高频乘性摄动或高频未建模动态抑制能力和对参考输入的复现能力，同时整个频段内满足S(s)+T(s)=I。

R(s)是参考输入r到控制输出u的传递函数矩阵，其增益表示对控制输出的抑制。

一般系统标称模型G0(s)不可能完全描述实际受控对象，即G0(s)存在不确定性ΔG(s)，实际模G(s)∈(G0(s)+ΔG(s)| ΔG(s ) ＜ ε)是一个有界的摄动范围区间。由鲁棒稳定性理论可知，如果控制器k(s)使标称系统G0(s)闭环稳定，则对于任意摄动ΔG(s)，系统仍闭环稳定的充分条件是:

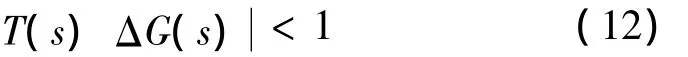
成立。如果有 ΔG(s )≤W3(s)成立，则式(12)等价于

W3(s)称为补灵敏度函数的加权函数。

对于外界干扰d，考虑其频谱特性，合理选择加权函数 W1(s)，使得 S(s)W1(s) ＜ 1成立，就能对闭环传递函数频域进行整形，从而抑制干扰d对系统输出的影响。

2.2 加权函数选择

混合灵敏度设计中加权函数选择是关键，合适的加权函数可以使系统获得良好的低频与高频性能。在系统高速旋转时，柔性转子较刚性转子而言会出现更多的固有模态振动，对柔性转子固有模态的识别有助于更好地进行振动控制。

本文采用力锤作为激振源，加速度传感器测量转子振动，并输入HP35670进行频谱分析，得到系统的前三阶固有频率如表2所示。

表2 系统的固有频率Tab.2 The natural frequency of system

由表2可知，本系统转子在15 000 r/min(250 Hz)转速范围内，会出现前二阶临界转速。为了保证系统安全稳定运行，本文根据转子在固有频率处的振幅选择加权函数，利用加权函数具有滤波器的作用，来减小系统不确定性的影响和抑制转子的振动。

由第1节计算得到的系统数学模型，其不确定性包括由电磁力线性化引起的参数不确定性和由各自由度之间的陀螺与惯性耦合引起的动态不确定性。其中参数不确定性主要考虑转子起浮时，位移刚度Ks和电流刚度Ki不确定性。

单自由度电磁力公式:

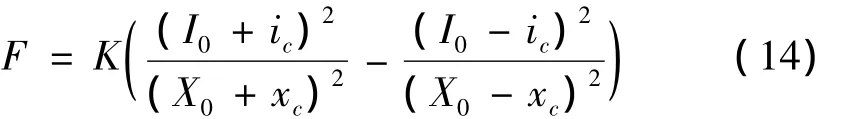
其中:K=0.25μ0N2A。将上式在平衡位置(X0，I0)附近进行前四阶泰勒展开，忽略高阶小项得:

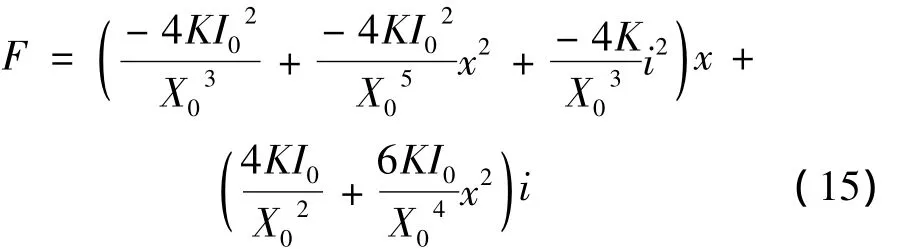
转子在刚起浮时非线性摄动最大，此时x=0.25 mm，i≈0.5A，以第1自由度为例，得到由参数摄动引起的乘性不确定性为Δ1(s):

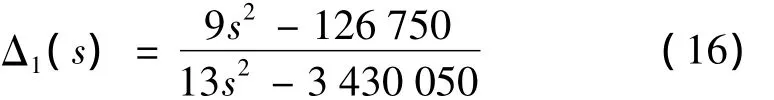
其中:Δ1(s)的奇异值特性曲线如图3所示。

转子惯性耦合描述同一平面内自由度间力或力矩耦合，陀螺耦合描述相互自由度之间的力或力矩耦合。由第1节的系统数学模型，当保留参数矩阵a21、b21非对角元，而忽略a22的非对角元素时，即系统只考虑考虑惯性耦合，不考虑陀螺耦合。此时径向第1自由度由惯性耦合引起的乘性不确定性为Δ2(s):

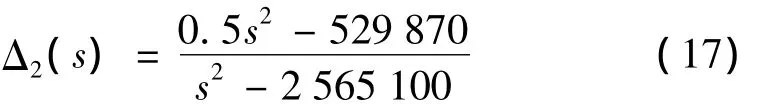
当保留参数矩阵a22的非对角元，而忽略a21、b21非对角元时，即系统只考虑考虑陀螺耦合，不考虑惯性耦合。此时径向第1自由度由陀螺耦合引起的乘性不确定性为Δ3(s):

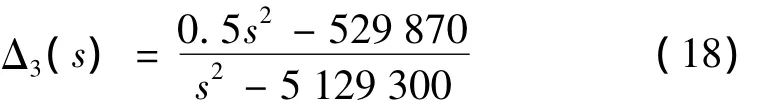
其中:Δ2(s)、Δ3(s)的奇异值见图3。根据加权函数的选择原则［10］，补灵敏度函数T(s)的加权函数W3(s)的奇异值曲线一般应在 Δ1(s)、Δ2(s)、Δ3(s)的上方，这样可以避免所求的控制器溢出。同时W3(s)应具有高通特性，但对低频特性没有特别要求。

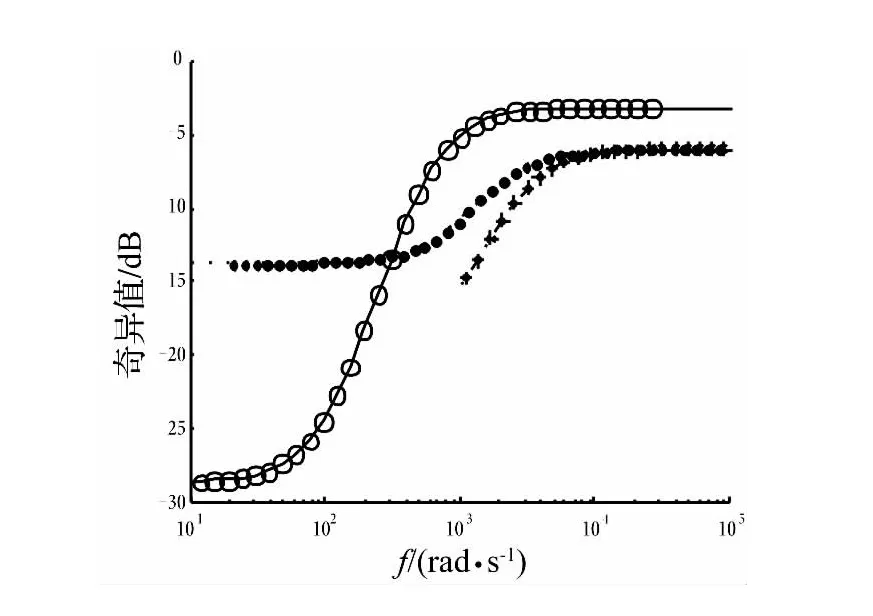
图3 不确定性奇异值曲线Fig 3 Singular value curves of uncertainty

转子的主要干扰为转子质量偏心引起的同频离心力干扰，其表达式为 Fd=mεω2cosωt，其中质量 m=7.533 2 kg，转子偏心ε=0.01 mm。由干扰引起的转子位移幅值为:

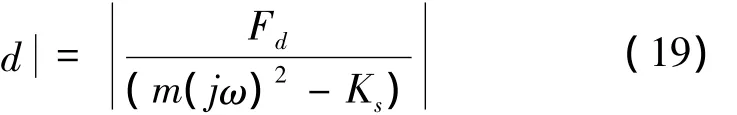
其中:Ks为位移刚度系数，以径向第1自由度为例，可计算得到固有频率f1=61.2 Hz和f2=221 Hz对应的同频干扰幅值分别为:

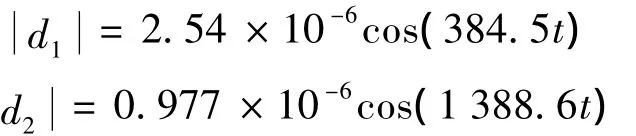
其余各自由度类似。在上述干扰下，为保证转子绕中心轴振动幅值xm不超过气隙长度(径向气隙为0.25 mm)的十分之一，即xm≤25μm，则期望灵敏度函数S(s)在 ω1=2πf1=384.5 rad/s最大幅值为:

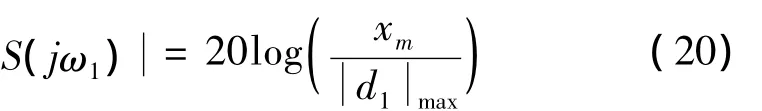
在 ω2=2πf2=1 388.6 rad/s最大幅值为:

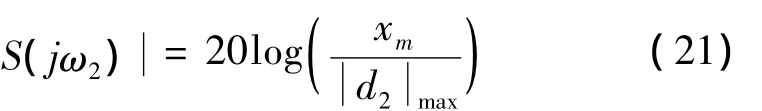
根据加权函数的选择原则，加权函数W1(s)的倒数在 ω1处应小于 S(jω1)、在 ω2处应小于 S(jω2)。同时W1(s)具有低通特性，其截止频率应小于W3(s)的截止频率，即高通与低通频带不重叠。

R(s)的加权函数为W2(s)，一般取比较小的常数，这样可以获得较大的系统带宽同时避免增加控制器的维数。综上，选取径向第1自由度加权函数选为:

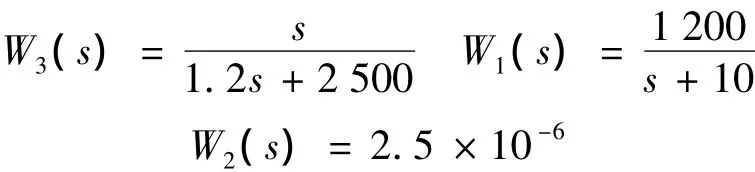
加权函数W3(s)和W1(s)的奇异值如图4所示，其满足上述加权函数的选择原则。

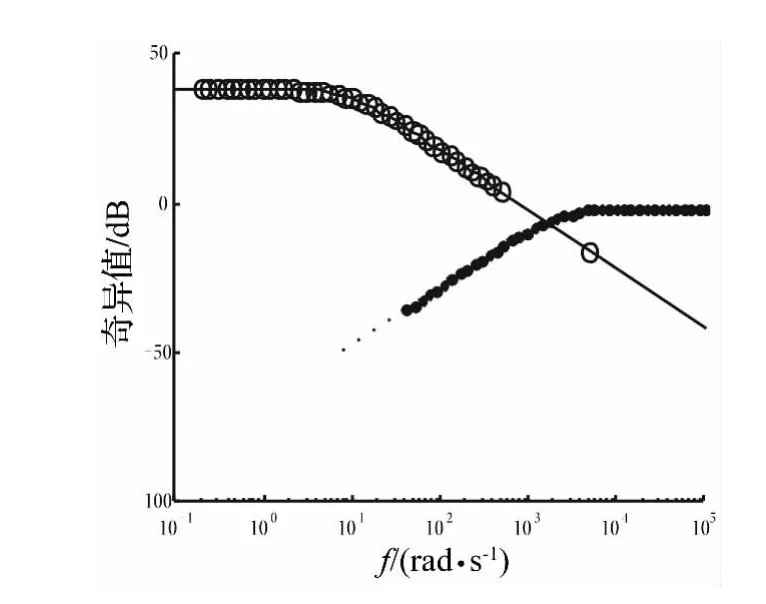
图4 加权函数奇异值Fig.4 Singular value of weighting function

2.3 控制器实现

由前述系统数学模型，径向第1自由度控制器传递函数可表示为:

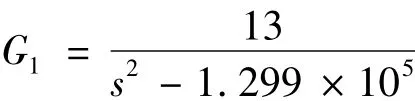
其余各自由度类似。由2.2节得到的径向第1自由度加权函数，利用matlab工具箱中Augtf()函数，可推得径向第1自由度增广系统p1(s)如下:

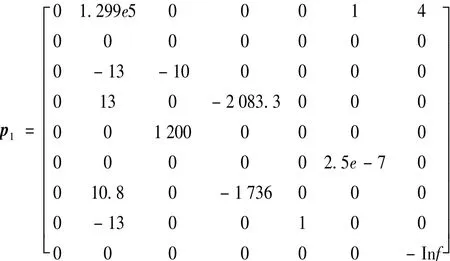
利用hinflmi()函数，径向第1自由度的H∞控制器k1(s)可表示为:

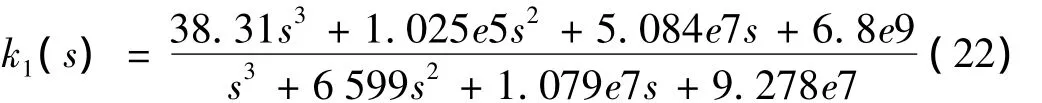
3 仿真与实验

3.1 试验系统的组成

图5为试验系统实物图，其中包括:传感器、控制器、PC机、功率放大器和机械受控部分。其中控制器为TI公司的TMS320F28335 DSP，该处理器具有高精度浮点运算能力，与PC机之间通过JTAG仿真器连接通信，采用CCS软件编写控制程序，实现系统主动控制。

图5 试验系统实物图Fig.5 Experiment setup of system

3.2 仿真与实验结果

利用matlab中simulink工具箱对H∞控制器和传统的PID控制器阶跃响应进行仿真对比。H∞控制器取式(22)形式，PID 控制器为:Kp(s)=2.5，Ki(s)=200/s，Kd(s)=0.03 s/(1+0.000 6 s)。

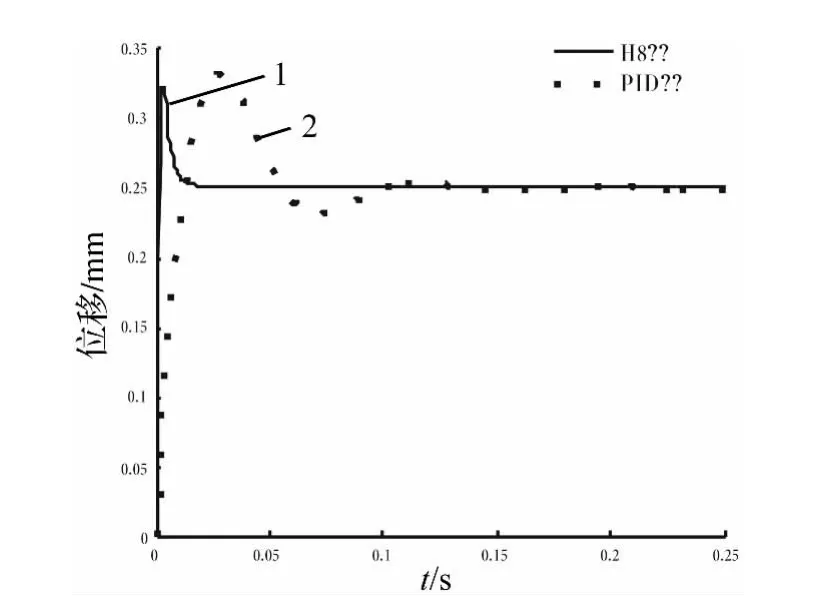
图6 阶跃响应对比Fig.6 Comparation of step response

由图6可知，曲线1为H∞控制，曲线2为PID控制。经比较可知，H∞控制的调节时间和超调量都较小。

根据式(22)，采用双线性变换得径向第1自由度的离散控制器如式(23)所示。

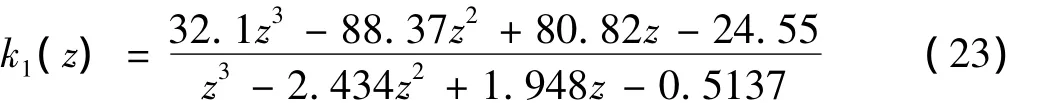
即可得到离散控制输出u1与输入e1的关系式:

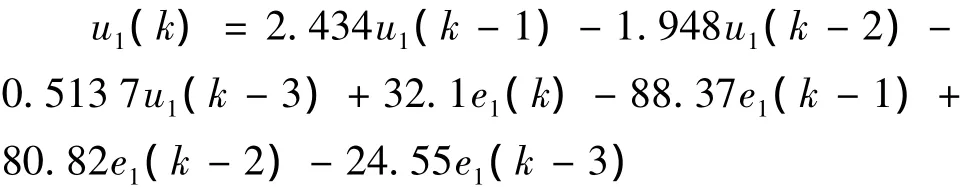
其余各自由度控制器与此类似。而PID控制器参数仍如前所示，经过PC机和CCS软件编程，调试通过后即可下载到DSP中进行实时控制。

图7是系统从0 r/min到15 000 r/min升速时，转子径向第1自由度的振动曲线图，其余各自由度与此类似。图7中，在3 900 r/min和11 400 r/min转速附近，两条曲线都存在两个明显的峰值，H∞控制曲线中两峰值分别为4.44μm和6.57μm;PID曲线中两峰值分别为6.31μm和7.2μm，H∞控制在临界转速处的振动幅值小于PID控制，其中第一阶临界转速处幅值减少29.6%，第一阶临界转速处减少8.75%。说明H∞控制策略能够更好地抑制固有频率处转子的振动，系统具有较强的鲁棒稳定性和较好的动态性能。

图7 转子振动曲线Fig.7 Vibration curves of the rotor

4 结论

(1)本文以五自由度磁悬浮轴承转子系统为对象，建立了系统数学模型，提出了根据转子在固有频率处的振幅选择加权函数的方法，采用混合灵敏度H∞优化控制理论，对被控对象的不确定性进行估计，获得加权函数W3(s)。

(2)利用激振试验，获取转子前二阶固有频率值，根据这两个固有频率处转子的同频振动幅值求得加权函数W1(s)，借助matlab的LMI工具箱，获得鲁棒控制器并应用于磁悬浮控制系统中。

(3)仿真和试验结果表明，本文所提出的抑制柔性转子固有频率处不平衡振动的加权函数选择方法有效可行，由此得到的H∞控制器能够保证磁悬浮轴承柔性转子系统高速运行，系统具有良好的鲁棒稳定性和抑制转子振动的能力。

［1］胡业发，周祖德.磁力轴承的基础理论与应用［M］.北京:机械工业出版社，2006.

［2］童水光，汪希萱.转子－轴承系统中电磁阻尼器理论研究［J］.振动工程学报，1992，5(1):17 －24.TONG Shui-guang，WANG Xi-xuan.Theory research on electromagnetc damper of rotor-bearing system［J］.Journal of Vibration Engineering，1992，5(1):17 －24.

［3］谢振宇，王 彤，张景亭，等.磁悬浮轴承金属橡胶环组合支撑转子系统的动态性能［J］.航空动力学报，2009，24(2):378－384.XIE Zhen-yu， WANG Tong， ZHANG Jing-ting， et al.Dynamic characteristics of active magnetic bearing system with metl rubber nnuluses［J］.Journal of Aerospace Power，2009，24(2):378 －384.

［4］张德魁，江 伟，赵鸿宾.磁悬浮轴承系统不平衡振动控制的方法［J］.清华大学学报，2000，40(10):28－31.ZHANG De-kui，JIANG Wei，ZHAO Hong-bin.Unbalance vibration control method of magnetic bearing system［J］.Journal of TSinghua University，2000，40(10):28 －31.

［5］Duan G R，Wu Z Y，Bingham C.Robust magnetic bearing control using stabilizing dynamical compensators［J］.IEEE Transaction on Industry Application，2000，36(6):1654－1660.

［6］ Duan G R，Howe D.Robust magnetic bearing control via eigenstructure assignment dynamical compensation［J］.IEEE Transaction on Industry Application，2003，11(2):204－215.

［7］Beals S，Shafai B.A adaptive force balance for magnetic bearing control system［C］.Conference on Decision and Control，Tucson，USA，1992:3535 －3539.

［8］ Tamisie V，Foni S，Lacour M，et al.Attenuation of vibration due to unbanlance of an active magnetic bearings milling elctro-spindle［J］.CIRP Annals-manufacturing Technology，2001，50(1):255 －258.

［9］ Kai Y L， Coppola V T， Bernstein D S. Adaptive autocentering control for an active magnetic bearing supporting a rotor with unknown mass inbalance［J］.Control System Technology， IEEE Transaction on Industry Application，1996，4(5):587 －597.

［10］吴旭东，解学书.H∞鲁棒控制中的加权阵选择［J］.清华大学学报(自然科学版)，1997，37(1):27 －30.WU Xu-dong，XIE Xue-shu.The selection of weighting function in robust control［J］.Journal of TSinghua University(JCR science editon)，1997，37(1):27－30.

［11］赵 雷，丛 华.可控磁悬浮轴承刚度与阻尼特性研究［J］.清华大学学报(自然科学版)，1999，39(4):96－99.ZHAO Lei， CONG Hua. Investigation of controllable magnetic levitation bearing stiffness and damping characteristics［J］.Journal of TSinghua University(JCR science editon)，1999，39(4):96－99.