3 圆弧滑面极限分析上限法

3 圆弧滑面极限分析上限法

3.1 圆弧滑面垂直条分法平移破坏机制

土坡塑性极限分析条分法是以极限分析上限定理作为理论基础的一种稳定性分析评价方法，因此，选择满足机动许可速度场的破坏机制就显得十分重要。根据所选择的破坏机制就可以建立虚功率方程，从而可推导稳定系数计算公式。

传统的条分法（刚体极限平衡理论）没有考虑土体的应力—应变关系，也不满足岩土材料遵循的相关联法则。相比较而言，土坡塑性极限分析条分法则在一定程度上克服了上述的缺点。同时，该方法在建立塑性极限破坏机制的过程中，采用了传统的条分法分条的思想，从而使得该方法的计算结果与条分法的计算结果具有较好的可比性。

土坡塑性极限分析条分法平移破坏机制的滑面或潜在滑面采用光滑曲线，该曲线可以为一般的圆弧、抛物线或其他拟合得到的光滑曲线。这样对滑面的假定是允许的，可以满足土坡稳定性分析评价的要求。陈惠发在其著作《极限分析与土体塑性》中指出：“在土坡稳定分析中，完整的分析方法应当考虑到所有可能的滑动面形状，并且满足一定的条件，因此，当然没有理由认为可以从这些条件导得一个能给出临界稳定条件的唯一解。显然，这是一个最优化问题。”（陈惠发，1995；龚晓南，1997）。根据陈惠发的研究结果可以得到结论，即在选择滑面形状时，应根据具体的工程地质条件和以往的研究成果，针对不同的情况合理地选用。

除了上述对滑面的假定外，塑性极限分析条分法平移破坏机制将土条视为刚体，而将滑面（潜在滑面）和条间接触带视为塑性体。当土坡产生滑动时，各土条合理的运动方向是向下的，且相关联流动法则要求滑面速度方向与滑面处有一夹角φ（见图3-1）。

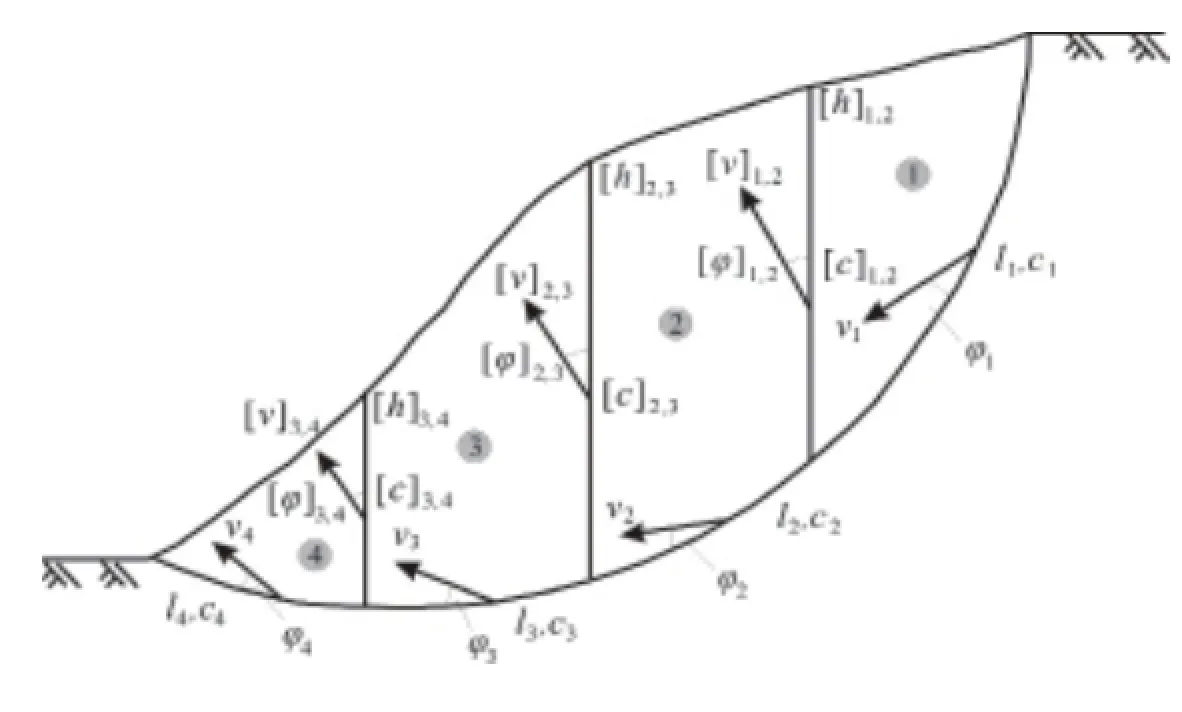
图3-1 土坡塑性极限分析条分法平移破坏机制（王根龙，等，2002）

根据条分法平移破坏机制土条为刚体的假定可知，在土条内部将不存在应力、应变，因此土条内部就没有内能的耗散（王根龙，2002）。在坡体内部，能量的耗散主要集中在滑面与竖向速度间断面上，因此，虚功率方程式可进一步简化为如下的形式

式中：Γ*为滑面和各竖向速度间断面；D为速度间断面上单位长度内能的耗散率；v*为机动许可的速度场；W为土重；T为作用在坡体上的外荷载。其中，间断面上的单位长度内能耗散率D公式为

相关联流动法则要求土条的速度v与速度间断面成φ角。相邻土条的滑面速度vi、vi-1与相邻土条间的竖向速度间断面速度[v]i,i-1，三矢量有闭合关系（见图3-2）。根据相邻土条的几何关系与矢量闭合关系，便可推导得出vi,vi-1,[v]i,i-1三者的速度递推关系公式（王根龙，2007）。

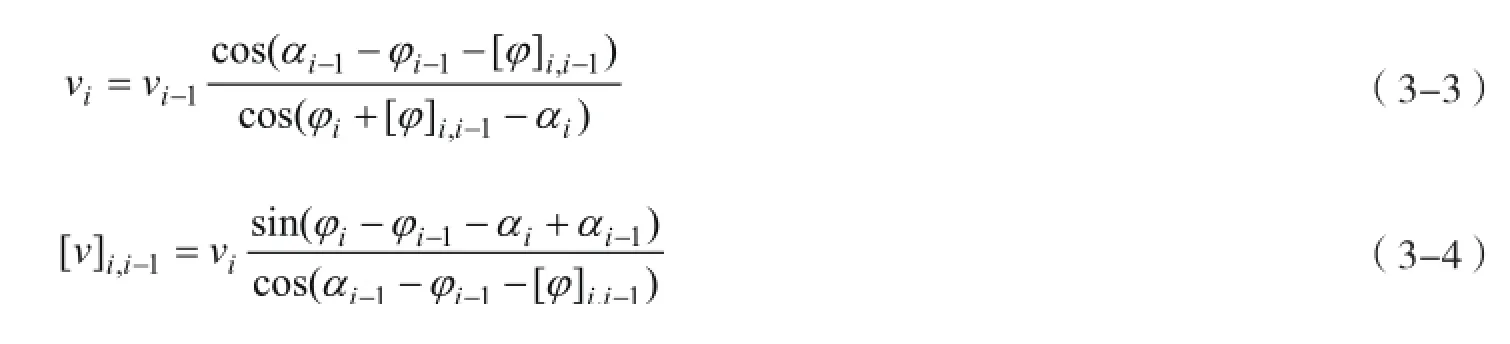
式中：[v]i,i-1为相邻土条间竖向速度间断面的相对速度；[φ]i,i-1为相邻土条间竖向速度间断面的内摩擦角；αi，αi-1为第i个土条与第i-1个土条滑面位置的倾角；φi，φi-1为第i个土条与第i-1个土条滑面位置的内摩擦角；vi，vi-1为第i个土条与第i-1个土条滑面位置的速度。

图3-2 速度矢量图

对于均质土坡，内摩擦角取恒定的φ值，此时速度矢量vi若从同一点引出，则可发现各竖向间断面的速度矢量[v]i,i-1位于同一条直线上，如图3-3（a）所示。由多层土组成的非均质土坡，各竖向速度间断面的内摩擦角[φ]i,i-1取不同的值，则相应的速度矢量[v]i,i-1不在同一条直线上。但上述两种情况下速度递推公式（3-3）、式（3-4）仍然成立。

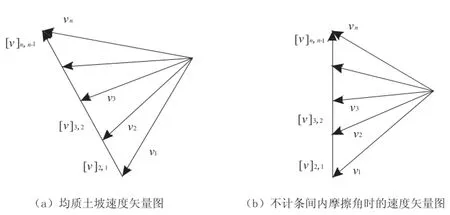
图3-3 均质土坡速度矢量图

3.2 圆弧滑面垂直条分法塑性极限分析稳定系数

为了得到土坡稳定性塑性极限分析条分法平移破坏机制的稳定系数计算公式，需根据作用于坡体上的外荷载和土体自重所做的外功率与塑性变形区的内部能量耗损率相等的条件建立起虚功率方程。由于已经假设土条为刚体，因此，坡体内部的能量耗损只发生在滑面和竖向速度间断面上。内部能量耗损率计算公式为

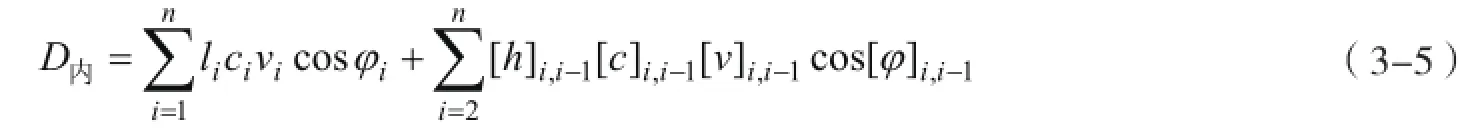
式中：等号右端第一项表示沿滑面的内能耗损率，其中li为第i个土条滑裂面长度，ci为第i个土条在滑裂面处的黏聚力；第二项表示竖向速度间断面的内能耗损率，其中[h]i,i-1为相邻的土条交线高度，[c]i,i-1为相邻土条交线处的黏聚力；其他符号意义同上。

当不考虑孔隙水压力及外部作用荷载产生的附加水平向荷载时，由土体自重和外部作用荷载产生的附加铅直向荷载所做的外功率计算公式为

式中：Wi为第i个土条的自重；Ti为外部作用荷载分配给第i个土条的铅直向附加荷载；其他符号意义同上。当土坡处于极限破坏状态时，根据内外功率相等的条件（D内=W外），即可建立虚功率方程。但应当注意，在虚功率方程中的力学参数c，φ并不是土坡正常工作状态时的值（或者说并不是由室内土工试验提供的试验参数），而应该是用来维持内外功率相等的岩土材料强度储备cd，φd值。

将式（3-5）代入式（3-6）中，再代入虚功率方程（D内=W外）中，整理后可得到土坡塑性极限分析条分法稳定系数的上限解计算公式

式中：φdi=tan-1(tanφi/K)；[φ]d(i,i-1)=tan-1(tan[φ]i,i-1/K)。

可以发现，式（3-7）等号右端的分子、分母中均含有速度矢量vi，vi-1和[v]i,i-1。因为上式是在土坡处于极限破坏状态条件下推导得出的，所以相应的速度矢量vi，vi-1，[v]i,i-1之间的递推式（3-3）、式（3-4）也应该取φdi，[φ]d(i,i-1)。在实际计算中，可以根据速度矢量vi、vi-1和[v]i,i-1之间的递推关系，将vi、vi-1和[v]i,i-1分别表示为第一个土条v1的关系式，进而可以消掉稳定系数计算公式中的所有速度项。由于该公式左右两端均含有K项，因此在计算时需要进行迭代。

当土坡为均质体时，速度递推公式（3-3）、式（3-4）可简化为

将式（3-8）、式（3-9）代入式（3-7），可得到均质土坡的稳定系数上限解计算公式：

式中：φd=tan-1(tanφ/K)。该公式同样需要迭代计算，一般是给K赋以初值K0，求出K0对应的cd，φd值，然后将cd，φd代入式（3-10）的右端，求出第一次迭代计算结果值K1，再求出K1对应的cd，φd值，重复上述的计算步骤求得第二次迭代计算结果值K2。给定一个阀值来结束迭代计算，则最后一次迭代计算得到的结果为土坡稳定性塑性极限分析条分法稳定系数最终解。根据这一迭代计算原理，由笔者编制了相应的Fortran电算程序，程序流程如图3-4所示。

图3-4 均质土坡稳定性计算流程图

如果不考虑土条间竖向速度间断面上能量的耗散，即[c]i,i-1，[φ]i,i-1均为零时，则[v]i,i-1是与计算无关的量。在这种简化条件下，速度递推关系公式为

相应的稳定系数计算公式也可简化为

3.3 有孔隙压力影响情况下的稳定系数

在土坡稳定性分析中，孔隙压力作为一种特殊的外部作用荷载，其影响也是一个很重要的因素（见图3-5）。如果片面地忽略孔隙压力的作用，则将会导致稳定系数偏于安全。这也将会给土坡的稳定性分析评价及治理工作造成一定的影响（王根龙，2002）。

图3-5 孔隙压力对土坡稳定的影响

孔隙压力有两种情况。一种是坡体内有地下水做稳定或不稳定的渗流。这时孔隙内即存在孔隙压力，可称为渗流压力。另一种是坡体内存在着未消散的超静孔隙压力，可称为超静压力。当坡体内有地下水的渗流作用，或部分浸在水下，或有超静孔隙压力作用时，都必须在稳定性分析中考虑孔隙压力的影响。

孔隙应力是由于孔隙水压力引起的，因此，孔隙应力也属于外部作用荷载产生的一种应力。反映在土坡稳定性塑性极限分析条分法的虚功率方程（W外=D内）中，则表现为孔隙应力对土粒骨架结构的作用所产生的孔隙应力功率，其功率表达式为

当把式（3-13）引入到土坡稳定性塑性极限分析条分法平移破坏机制中时，考虑到土条为刚体的假定，因此，在土条内部没有应力—应变，或者说孔隙应力在土条内部没有产生外功率。根据以上的分析可知，孔隙应力在条分法平移破坏机制中所做的外功率主要集中在滑面和竖向速度间断面上，其公式为

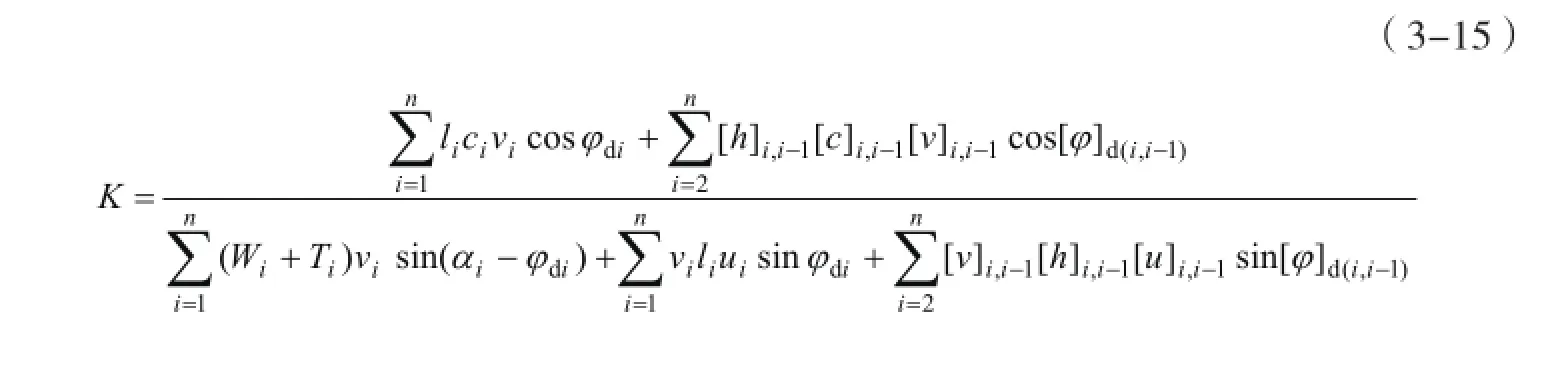
式中：φdi=tan-1(tanφi/K)；[φ]d(i,i-1)=tan-1(tan[φ]i,i-1/K)。vi、vi-1和[v]i,i-1三者之间的速度递推关系由式（3-3）和式（3-4）确定。可以发现该式中的K仍是以隐式出现，因此计算时须利用迭代的方法实现。

当忽略条间的内外功率时（[c]i,i-1=0，[φ]i,i-1=0），上式可简化为

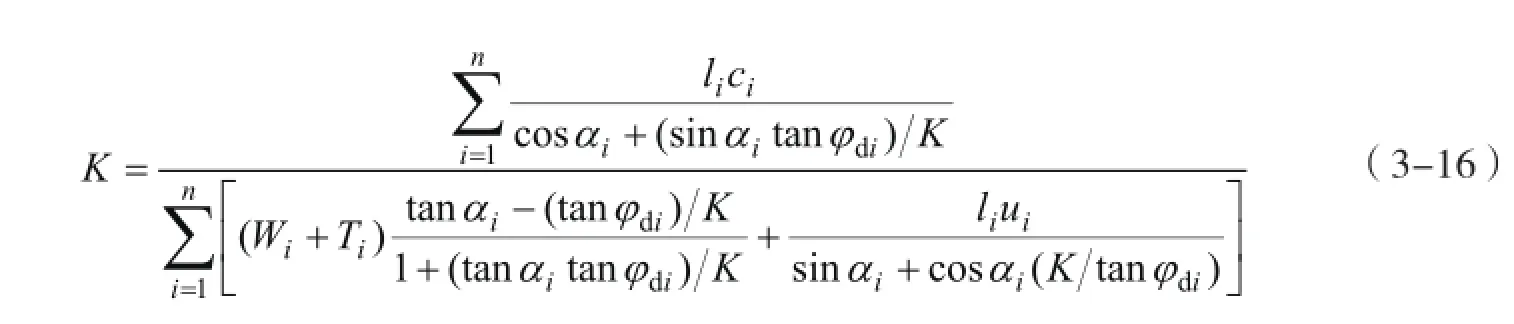
3.4 圆弧滑面径向分条模式上限解

土质边坡稳定性分析计算通常采用垂直分条的方法（Fellenius，1927），这是一种平动的变形破坏模式，但是从运动学方面来看，土体在滑动时是做平面运动的，既有平动，也有转动，而基于刚体极限平衡理论的垂直条分法不能很好地体现转动的特点。萨尔玛（1973）、Donald 和 陈祖煜（1997）分别从刚体极限平衡理论和塑性极限分析理论提出了斜分条法，实现了对垂直条分法的改进。寇日明（1998）从刚体极限平衡理论出发，尝试做过径向条分法的研究工作，但缺点是计算公式繁琐，很难被工程应用。笔者从极限分析上限定理出发，在参考了滑移线场理论、垂直分条法和斜分条法之后，提出了一种新的土质边坡稳定性分析计算方法——极限分析径向条分法（王根龙，2007），并建立了极限分析径向条分法的破坏模式，推导得到了稳定系数计算公式。关于垂直分条、斜分条及径向分条三种方法的比较如表3-1所示。

滑移线法对于径向分条模式的提出有很大的指导作用。首先回顾一下滑移线理论（Drucker和Prager，1952），当材料处于塑性状态时，每一点都存在两个剪切破坏面。把各点的剪切破坏面（或称滑移面）连续地联结起来，可以得到两组曲线，称为滑移线。滑移线法就是根据由平衡方程和屈服条件得到的基本方程，采用求解偏微分方程的滑移线理论得到特征线方程，其特征线η和ξ恰好是满足摩尔-库仑强度准则的滑裂面。因此建立在特征线上的求解方法也称为滑移线法，而最终获得的η和ξ线，即为处于极限状态的塑性区的滑裂面。滑移线上一点的切线方向就是相应点的滑移面方向。

表3-1 三种条分法的对比

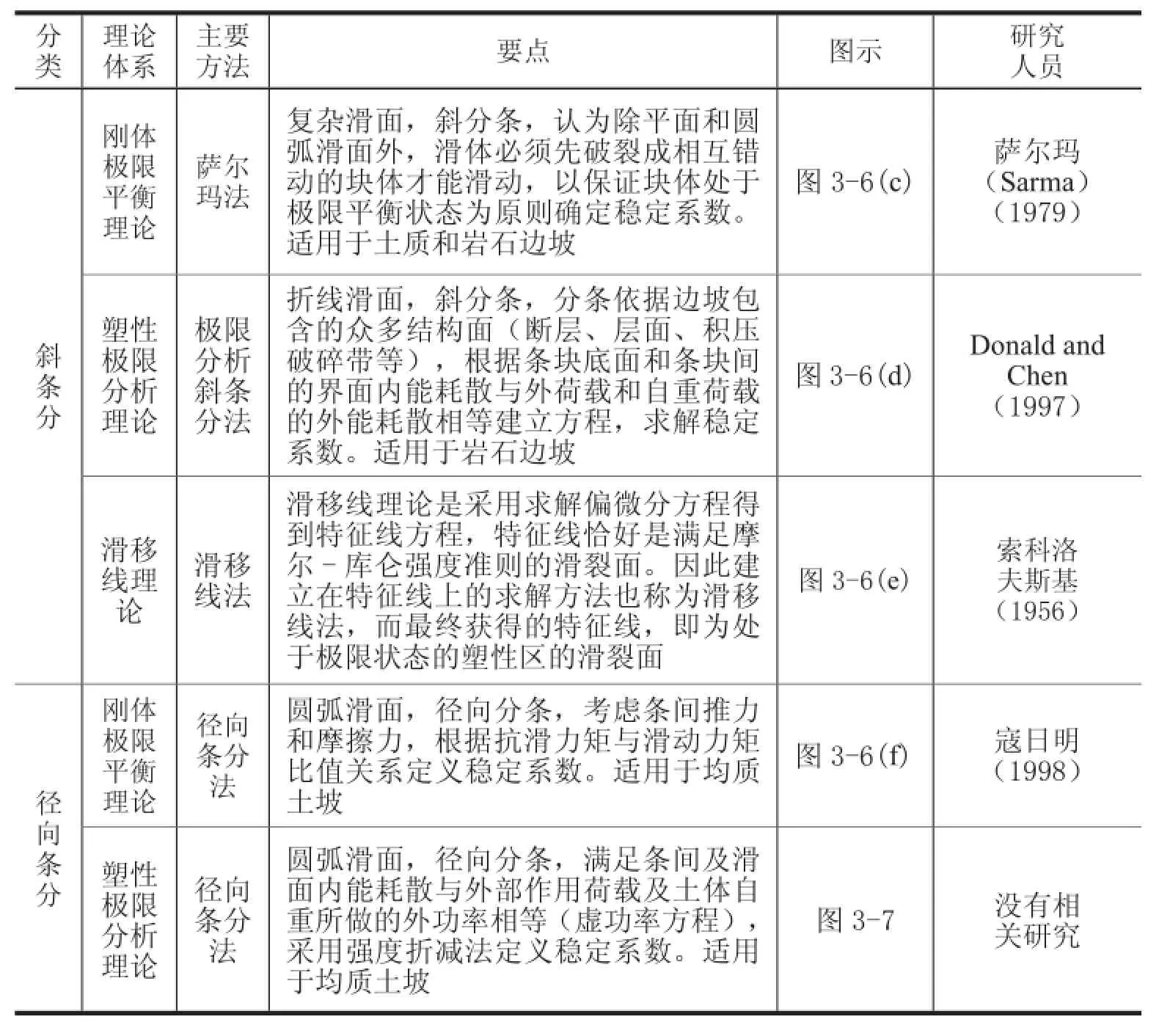
（续表）

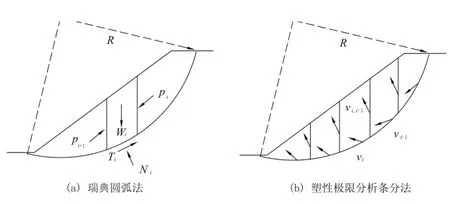
图3-6 三种条分法的典型图示

根据该理论可以得到破坏土体内两组代表剪切破坏的滑移线，这两组线恰好是径向分条法中的滑裂面和倾斜条块界面，因此可以发现，建立径向条分法时用到的圆弧速度间断面（滑面）可以采用滑移线场理论的滑裂面，而径向分条形成的倾斜速度间断面可以采用滑移线场理论的倾斜条块界面。这就为极限分析径向条分法找到了一个理论上可行的依据，根据这种径向分条法分析边坡稳定性，一般可以得到与实际比较接近的边坡破坏模式，这一点是刚体极限平衡方法做不到的。从另外一个角度考虑，实际上极限分析上限解和滑移线理论解是一致的，同属于一个理论体系。若能建立与滑移线场对应的速度场，而且满足机动场的要求，则极限分析上限解就是滑移线法解。

根据极限分析上限定理，在土质边坡中存在两组速度间断线，第一组是圆弧滑线，第二组是径向分条后土条间速度间断线。当考虑库仑材料为刚塑性体时，边坡便可以分为刚体和速度间断两部分。土条内部被定义为刚体，因为刚体在受力时，不发生变形，或者说没有应力、应变产生，所以土条内没有内能的耗散；圆弧滑线和土条间过渡带被定义为速度间断线，由于速度在条间过渡带内发生急剧而连续的变化，因此，在该薄层塑性变形区内将有内能的耗散。根据正交法则，速度向量必须以内摩擦角φ倾斜于速度间断面。这种间断面可以被认为是连续速度场的极限情况。在这种情况下，速度分量（一个或多个）在跨越窄过渡层时变化很快，因而为了方便起见，可以用间断面来代替。间断速度场不仅提供了方便，而且往往还可获得实际的破坏模式或破坏机制。

为了使由n个条块组成的机构（见图3-7）位移是协调的，就要求相邻两个条块的移动不能导致它们重叠或分离，或者说要求相邻条块（以第i和第i-1条块为例）底面的速度vi，vi-1与径向条块间垂直界面的相对速度vi,i-1组成的速度矢量要闭合（见图3-8）。根据矢量闭合的几何关系，便可以得到速度关系公式

式中：θi，θi-1，θi,i-1为速度与x轴的夹角，均定义为从正方向开始逆时针旋转为正，同时，0≤θ≤2π。

式中：αi，αi-1为第i和第i-1个径向土条底滑面与水平方向的倾角。将式（3-19）和式（3-20）代入式（3-17）和（3-18）中，整理后可以得到

式中：δ为圆弧滑面经过径向等分条后，每段滑弧对应的圆心角，当滑面和分条数n确定后，δ也为定值，其公式为δ=αi-1-αi。由此看见，B为常数，或者说径向土条底滑面对应速度{vi}（i=1,2,…,n）是公比为常数B的等比数列。对于式（3-22）也可以得到同样的结论。根据等比数列的通项公式，vi与vi,i-1可以表示为第1个径向条块速度v1的关系式。

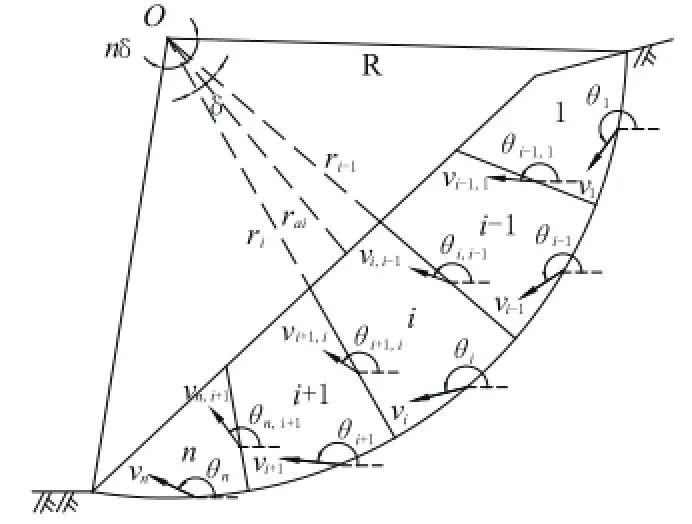
图3-7 径向分条法极限分析破坏机制

图3-8 径向条分法速度向量

为了得到土质边坡极限分析稳定系数上限解，需要根据外部作用荷载和土体自重所做的外功率与塑性变形区的内部能量耗损相等的条件建立虚功率方程。因为径向土条被视为刚体，因此土条内没有能量损失，但径向土条之间和圆弧滑面是速度间断面，在这些间断面上将会产生能量的耗损，其大小为:

式中：l为土条底滑面长度（m）；c为均质土体的内黏聚力（kPa）；φ为均质土体的内摩擦角（弧度）；ri' 为第i个径向土条长度，ri'=R-ri（m）。

虚功率方程右侧代表外部作用荷载和自重荷载产生的外功率。当不考虑地震惯性力、坡体上外荷载和孔隙水作用时，仅仅考虑径向土条的土体自重所做的外功率时，其大小为

式中：Wi为第i个径向土条的重量（kN·m-1）。在计算Wi时，将每个土条面积作为两个扇形之差，外半径为R，内半径为rai=(ri+ri-1)/2，对于第1个径向土条和第n个径向土条，内半径分别为(R+r1)/2和(rn-1+R)/2，从而有

虚功率方程是建立在边坡临界极限状态条件下的，为了使边坡处于临界破坏状态，可以采用材料强度折减法的概念。其定义是：沿某一滑面的实际工作状态的力学参数c，tanφ与用来维持边坡内外功率相等的换算力学参数clim，tanφlim之比，关系表达式为K=c/clim=tanφ/tanφlim。根据式（3-23）、式（3-24）、式（3-25）和式（3-26），可以得到径向条分法的土质边坡极限分析法稳定系数上限解公式为

式中：φlim=tan-1(tanφ/K)，该公式需要迭代计算，一般是给K赋以初值K0，求出K0对应的clim，φlim值，然后将结果代入式（3-28）的右端，求出第一次迭代计算结果值K1，再求出K1对应的clim，φlim值，重复上述的计算步骤求得第二次迭代计算结果值K2。通过给定一个阀值来结束迭代计算，一般取相邻两次稳定系数差的绝对值小于10-6，则最后一次迭代计算得到的结果为稳定系数解。

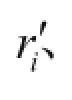
以某一均质土坡为例，高12.2m，坡面坡度为1∶2，土的内摩擦角φ=20°，黏聚力c=29kPa，容重γ = 18.8kN·m-3。根据瑞典圆弧法对这个边坡进行最危险滑面搜索，得到了如图3-9的圆弧滑面，对应稳定系数K=2.08。采用极限分析径向条分法对搜索到的最危险滑面进行计算，分条数n=10，每个径向土条对应圆心角δ和弧长l分别为0.169Rad和4.13m，滑弧半径R为24.4m。通过式（3-23）和式（3-24）计算得到常数Α=0.2057，B=1.1529，其他数据见表3-2。将数据代入稳定系数计算公式（3-28）中得到K=2.05，与瑞典圆弧法计算结果很接近。为了对比极限分析径向条分法与瑞典圆弧法，笔者又用其他一些算例进行了比较，其误差都不超过5%。

图3-9 径向条分法计算实例

表3-2 径向条分法计算剖面数据