边坡滑面正应力构成及分布模式选择
卢坤林 ,朱大勇 ,杨 扬
(1.合肥工业大学 土木与水利工程学院,合肥 230009;2.合肥工业大学 安徽省土木工程与材料省级重点实验室,合肥 230009)
1 引 言
极限平衡法一直是边坡工程中最常用的稳定性分析方法,历经多年发展,到目前已相当完善。在整个发展的过程中,学者们一直将多余未知量的假设选在条间作用力或作用位置上[1],直到Bell[2]、朱大勇[3]和郑宏[4]等将研究视线转到滑面正应力的分布模式上来,他们将滑面正应力分布假设为含两个待定参数的函数,根据整个滑体的3 个平衡条件,建立了含安全系数和两个待定参数的3 个方程组,通过数学推导获得了安全系数的显示解答。该方法与其他严格的条分法相比,求解过程更便捷、易于编程实现且不存在收敛性问题。
笔者认为,恰当合理的滑面正应力分布模式是获得安全系数正确解答的前提,刘华丽[5]和郑宏[6]等均对此有过探讨。目前,关于滑面正应力的假定模式,Bell[2]提出的公式为

朱大勇等[3]则提出的公式为

朱大勇等[7]推导出的公式为

杨明成[8]的公式为

郑宏等[4]的公式为
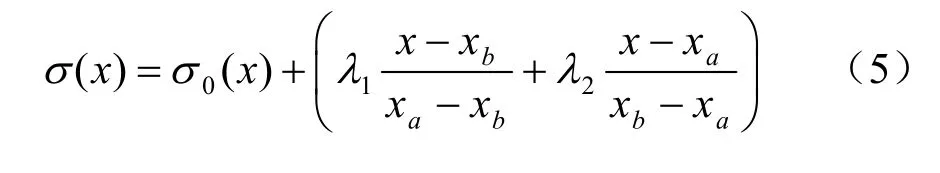
上述假定模式中的 λ1和 λ2均为待定参数, xa、xb为滑面两端点x 坐标,其他均为已知函数(量),具体意义请查阅对应的参考文献,此处从略。另外,为了表述统一,符号也作了调整。
由于不同学者采用的假设模式各异,为了规范假设模式,完善此类极限平衡法的理论基础,还需要对滑面正应力的假设模式进行进一步研究。本文首先分析了滑面正应力的构成以及各组成部分对滑面正应力的贡献大小,据此建议了具有理论基础的滑面正应力分布模式。
2 滑面正应力修正法的基本过程
本节旨在介绍基于滑面正应力假定的极限平衡法基本过程,更详细地分析可见朱大勇[3]或郑宏等[4]的相关研究论文。
图1 为具有一般形状滑动面的边坡,滑面为y = s ( x),坡面为 y = g ( x)。单位宽度的土条重为w( x ),水平地震惯性力为 kcw( x ), kc为地震影响系数。坡面上作用有 qx( x )和 qy( x )的水平和竖向荷载。滑面上的正应力和剪应力分别为 σ( x)与τ ( x),孔隙水压力为 u ( x )。
在滑面 y = s ( x)上,由摩尔-库仑强度准则:

式中:sF 为安全系数;c、φ 分别为滑面黏聚力与内摩擦角。
根据滑体的静力平衡条件,可建立水平、竖向以及绕任意一点(xc,yc)力矩的3 个平衡方程:
式(7)~(9)构成了关于安全系数的平衡方程组,若能确定滑面正应力 ( )xσ 的分布,求解式(7)~(9)即可得到安全系数。
3 滑面正应力σ (x)的构成分析
图2 为滑体中任一土条的受力分析示意,其中E 和T 分别为条块间水平和竖向作用力, h 和ht分别为条块高度和条间力作用点高度,条块宽度为Δx,其他符号意义同前。假定条块的宽度无限小,两个方向的平衡方程分别为

根据式(6)的摩尔-库仑强度准则,式(10)、(11)改写为

式中:ψ0= tanφ /Fs, c0= c /Fs。

图2 普通土条受力分析 Fig.2 Forces acting on a general slice
由式(12)和式(13)可得

由式(14)可见,滑面正应力由两部分组成,一部分为滑体体积力和坡面外力对滑面正应力的贡献(记为0( )xσ );另一部分由土条间作用力对滑面正应力的贡献(记为1( )xσ ),则式(14)简记为
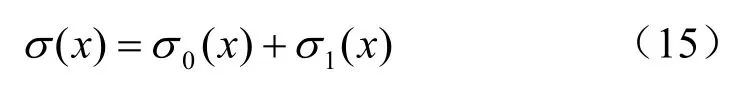
其中:
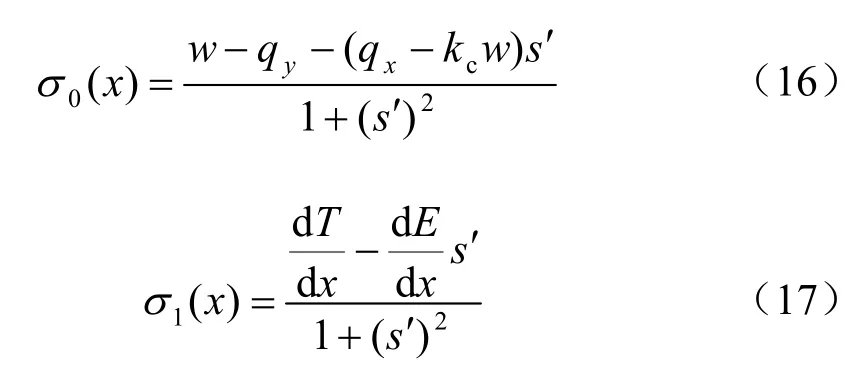
由式(16)、(17)可知, σ0( x)在滑面已知前提下属于已知函数;因无法准确获得条间作用力的具体分布模式, σ1( x)仍不能准确得到。目前,极限平衡分析方法中瑞典法假设所有条间力为0、简化Bishop 法假定条块间作用力为水平、简化Janbu法假定条块间的剪应力为0、Spencer 法假定条间力倾角为一个常数、Morgenstern-Price 法(简称M-P法)则假定条间法向力和剪切力之间的关系为T ( x) =λf ( x ) E ( x)。下面以算例来讨论这些条间力分布模式下的滑面正应力 σ( x)以及 σ0( x)和 σ1( x)的分布。
所举算例边坡如图3 所示,有两个潜在的滑动面,即圆弧形和一般形状滑动面。边坡共有4 个地层,其物理力学参数列于表1。此外,边坡还受水压力和地震力作用,地震影响系数为0.1。
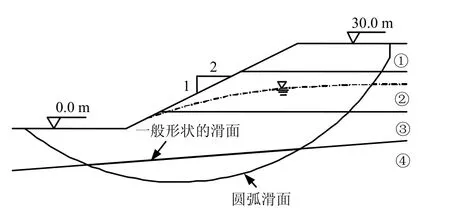
图3 边坡剖面图及滑面 Fig.3 Cross-section of slope and slip surface

表1 边坡地层参数 Table 1 Properties of slope soils
采用已有的条分法对条间作用力的假设,分别计算了简化Bishop 法、简化Janbu 法、Sarma 法、Spencer 法、M-P 法和严格Janbu 法共计6 种模式,根据每个土条平衡条件可获得滑面正应力 σ( x)以及两个贡献分量 σ0(x)和σ1(x)的分布,并将每种假设情况的计算结果绘在一张图中便于比较,如图4、5 所示。
由图4、5 可知:①滑体体积力和坡面外力对滑面正应力的贡献(0( )xσ )占主导地位,土条间作用力对滑面正应力的贡献(1( )xσ )是非常有限的。②滑面正应力 ( )xσ 以及0( )xσ 和1( )xσ 均为单值、连续、近似光滑的曲线(尤其是圆弧滑面),所以能够构造适当的函数予以逼近拟合。
4 滑面正应力分布对安全系数的影响
对于严格满足所有平衡条件的极限平衡法,不同条间力的假设对安全系数的影响较小。Duncan[9]指出,对圆弧滑面安全系数变化幅度小于5%,任意形状滑面安全系数变化幅度也在13%以内。换言之,条间力的假设不同将会影响滑面正应力的分布,由此可间接得到:只要满足所有平衡条件,滑面正应力的分布对安全系数的影响也较小。
刘华丽等[10]采用了五点插值的3 次样条函数构造了不同的滑面正应力分布形式,讨论了滑面正应力分布对安全系数的影响。研究结果表明:满足全部平衡条件下,滑面正应力分布的两个极端安全系数相差在19%以内,若再考虑条间力的合理性检验,则降低到7%。可见,在满足平衡条件和合理性的前提下,滑面正应力的分布对安全系数影响不显著。

图4 各条间力假定模式下的滑面正应力分布(圆弧滑面) Fig.4 Normal stress distributions of circular slip surface with different calculations

图5 各条间力假定模式下的滑面正应力分布(一般滑面) Fig.5 Normal stress distributions of general slip surface with different calculations
讨论上一节中算例在各种滑面正应力分布下的安全系数,表2 仅给出了满足所有平衡条件的滑面正应力及对应安全系数。计算结果可见,在满足平衡条件和力学合理性的前提下,不同的滑面正应力模式间的安全系数最大相差4%以内。
某均质的、无体重的、受垂直均布表面荷载的斜坡,其基于塑性力学的解已经得出[11]。如图6 所示,斜坡高度为10 m,坡角为45°,抗剪强度参数 分别为c=10 kPa、φ=30°。斜坡顶部的最大垂直超载为111.4 kPa。

表2 不同滑面正应力分布下的安全系数 Table 2 Safety factor corresponding to different distributions of normal stresses

图6 构造滑面正应力分布与解析解分布对比 Fig.6 Comparison of normal stress distribution between analytic solution and that of constructed slip surface
滑面正应力假设模式采用式(2)计算,得出的安全系数是1.032,与理论分析的结果(1.000)相比,误差较小,推力线位置也非常吻合,但滑面正应力的分布曲线与理论解答完全不一致,如图6 所示。再次说明只要满足平衡条件,滑面正应力分布对安全系数影响不显著。
综合前人研究结论及本节算例结果,可以得到如下结论:在满足平衡条件和力学合理性的前提下,安全系数对滑面正应力分布不甚敏感。当然,这一结论仍是经验性的,目前还缺少严格的数学证明。
5 滑面正应力分布函数的构造
为了方程组(7)~(9)能够求解,必须构造滑面正应力分布函数。笔者认为,恰当的构造函数应该考虑滑面正应力分布的力学构成、力学合理性以及对安全系数解的稳定性。因此,建议采用以下构造函数:

式中:0( )xσ 由式(16)确定; ( )f x 为逼近函数,为了式(7)~(9)的求解,可含有两个待定参数。
式(18)中第1 项为滑体体积力和坡面外力对滑面正应力的贡献分量,第2 项为土条间作用力对滑面正应力的贡献分量,因无法准确获得,采用逼近函数 ( )f x 来近似反映。
前文研究已经表明,滑体体积力和坡面外力对滑面正应力的贡献分量占主导地位,土条间作用力对滑面正应力的贡献分量占次要地位,因此,构造函数以占主导地位的0( )xσ 为核心函数,采用含有两个待定参数的 ( )f x 逼近1( )xσ 是符合实际力学构成的。
前文研究还得出了安全系数对滑面正应力的分布不敏感的结论,同时逼近函数 ( )f x 对滑面正应力的贡献是非常有限的。所以,无需过分追求 ( )f x 与真实分布1( )xσ 之间的吻合度,可以选用线性函数逼近:

笔者所在的课题组曾研究过[12],采用线性逼近函数能够较好地满足条间力的合理性检验,有时仅在端部小范围不能满足,一般通过设置拉裂缝予以消除(这也是符合实际情况的)。
由于安全系数对滑面正应力的分布不敏感,因此,对构造函数的微小扰动不会造成安全系数大幅变化,即式(18)的构造函数还满足解的稳定性要求。
6 讨 论
6.1 关于逼近函数f(x)的作用
滑面正应力分布中的逼近函数起到了两方面的作用。一是反映土条间作用力对滑面正应力的贡献分量;二是调节滑面正应力的分布,使其满足所有的平衡方程。
结合图6 成果,笔者认为,第1 个作用非常有限,似乎也没有必要非常精确逼近;而第2 个作用则非常必要。已有研究表明,严格极限平衡法得到的安全系数差别不大,而与不能够完全满足所有的平衡条件得到的安全系数差别却比较大。为了满足所有平衡方程,采用 ( )f x 调节滑面正应力的分布,以便得到准确度较高的安全系数,因此, ( )f x 亦可称为修正函数。
6.2 关于σ 0(x)的选择
朱大勇[7]和刘华丽等[5]分别讨论了0( )xσ 的选择对安全系数的影响,结果表明:0( )xσ 的选择对圆弧滑面安全系数影响为5%以内,一般形状滑面能够达到15%。为了消除0( )xσ 的选择带来的不确定性,本文建议采用式(16)来计算0( )xσ 的分布。
7 结 论
(1)滑面正应力由滑体体积力(含坡面外力)和土条间作用力这两部分贡献分量构成。其中,滑体体积力(含坡面外力)贡献分量占主导地位,而土条间作用力的贡献分量较小。
(2)在满足平衡条件和合理性的前提下,安全系数对滑面正应力分布不敏感。因此,在滑面正应力分布函数的构造上无需过分追求与真实分布之间的吻合度,可采用以占主导贡献地位的滑体体积力(含坡面外力)贡献分量为核心函数,选用含两个待定参数的修正函数来逼近土条间作用力贡献分量的分布。
(3)建议了一种滑面正应力构造函数的模式,使滑面正应力的假设模式规范化,避免了不同构造函数对安全系数的影响,完善了此类极限平衡法的理论基础。
[1] 钱德玲. 土力学[M]. 北京:中国建筑工业出版社, 2009.
[2] BELL J M. General slope stability analysis[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1968, 94(SM6): 1253-1270.
[3] ZHU D Y, LEE C F. Explicit limit equilibrium solution for slope stability[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2002, 26(15): 1573-1590.
[4] ZHENG H, THAM L G. Improved Bell’s method for the stability analysis of slopes[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(14): 1673-1689.
[5] 刘华丽, 朱大勇, 刘德富, 等. 边坡安全系数的多解性讨论[J]. 岩土力学, 2007, 28(8): 1661-1664. LIU Hua-li, ZHU Da-yong, LIU De-fu, et al. Discussion on multiple solution of safety factor of a slope[J]. Rock and Soil Mechanics, 2007, 28(8): 1661-1664.
[6] 郑宏, 谭国焕, 刘德富. 边坡稳定性分析的无条分法[J].岩土力学, 2007, 28(7): 1285-1291. ZHENG Hong, THAM L G, LIU De-fu. A slice-free method for stability analysis of slopes[J]. Rock and Soil Mechanics, 2007, 28(7): 1285-1291.
[7] 朱大勇, 李焯芬, 姜弘道, 等. 基于滑面正应力修正的边坡安全系数解答[J]. 岩石力学与工程学报, 2004, 23(16): 2788-2791. ZHU Da-yong, LEE C F, JIANG Hong-dao, et al. Solution of slope safety factor by modifying normal stresses over slip surface[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(16): 2788-2791.
[8] 杨明成. 一般条分法的安全系数显示解[J]. 岩土力学, 2004, 25(增刊2): 568-573. YANG Ming-cheng. Explicit solution to safety factor for general slice method[J]. Rock and Soil Mechanics, 2004, 25(Supp.2): 568-573.
[9] DUNCAN J M. State of the art: limit equilibrium and finite element analysis of slope[J]. Journal of Geotechnical Engineering, ASCE, 1996, 122(7): 577-596.
[10] 刘华丽, 朱大勇, 钱七虎, 等. 滑面正应力分布对边坡安全系数的影响[J]. 岩石力学与工程学报, 2006, 25(7): 1323-1330. LIU Hua-li, ZHU Da-yong, QIAN Qi-hu, et al. Effect of normal stress distribution on factor of safety of a slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1323-1330.
[11] SOKOLOVSKI V V. Statics of soil media. Translated by Jones D H, Schofield A N[M]. London: Butterworths Scientific Publications, 1960.
[12] 朱大勇. 极限平衡法的显示解与统一格式[R]. 南京: 河海大学, 2002.

