泥石流流速横向分布特征与防治工程结构优化

徐林荣，韩 征, ，苏志满, ，吴 强

（1.中南大学 土木工程学院，长沙 410004；2.九州大学 工学府，福冈 819-0395；3.中国科学院成都山地灾害与环境研究所，成都 610041）

1 引 言

随着我国的社会经济发展，特别是西部大开发及四川地震灾区的恢复和建设的进行，山区泥石流的危害越来越大，正确地防治泥石流灾害已刻不容缓[1－2]。泥石流防治的主要问题是泥石流冲击及磨蚀荷载的确定[3]，而荷载的确定主要涉及到泥石流流速的计算，因此，泥石流流速的分布和计算作为泥石流防治工程设计的核心问题之一，就成了研究中的重点和难点[4]。

现有流速计算公式主要分为地区性经验公式与理论模型公式两类，国内采用较多的是基于曼宁（Manning）公式从观测资料出发建立的一些地区性的经验公式[5－8]，如云南东川泥石流流速改进公式、甘肃武都柳湾沟流速公式和西南地区（铁二院）流速公式等。在国外，有学者提出了一些经验公式，如Koch经验公式[9]，也有学者基于宾汉流体、膨胀流体、黏塑性流体等理论模型，推导了泥石流阵性流动方程，如高桥保的颗粒流膨胀体流速公式[10]、牛顿体紊流的Manning-Strickelr公式[11]以及明流渠谢才公式[12]等。然而，这些公式的计算结果均为平均流速[4]，未对流速横向分布情况加以考虑，在实际工作中具有很大的局限性，给泥石流防治结构的抗冲击、抗磨蚀设计带来了极大困难。

目前，泥石流流速横向分布方面尚无深入研究[13]，已有成果主要以现场观测记录的统计分析为基础，如康志成等[14－15]基于东川蒋家沟的观测，判断了泥石流表面流速中间大、两侧小的特点，并指出了泥石流平均流速仅为中泓线流速的0.3～0.4倍。Tecca等[16]利用1998年监测到的意大利Acquabona流域的泥石流运动录像资料，估算了泥石流表面流速分布。这些研究成果对流速横向分布进行了定性的判断，缺乏相应的理论基础，因此，韦方强等[13]就指出，泥石流流速分布研究是今后泥石流流速研究的最重要方向，必须争取在泥石流横向流速分布和垂向流速分布方面获得突破性进展。本文以四川省理县地震灾区甲司口沟在建泥石流防治工程为对象，研究泥石流流速的横向分布情况及相应的工程优化措施。

2 基本假设与公式选用

2.1 基本假设

（1）所取断面位置处于泥石流冲淤平衡状态，无显著淤积或物源补给，即通过该断面的流量数值上等于采用雨洪法计算所得的断面流量。

（2）将泥石流流体简化为连续介质，并假设泥石流流面保持水平或近似水平。

（3）将泥石流沟道横截面的原始地面线理想化为V 型线（见图1）。

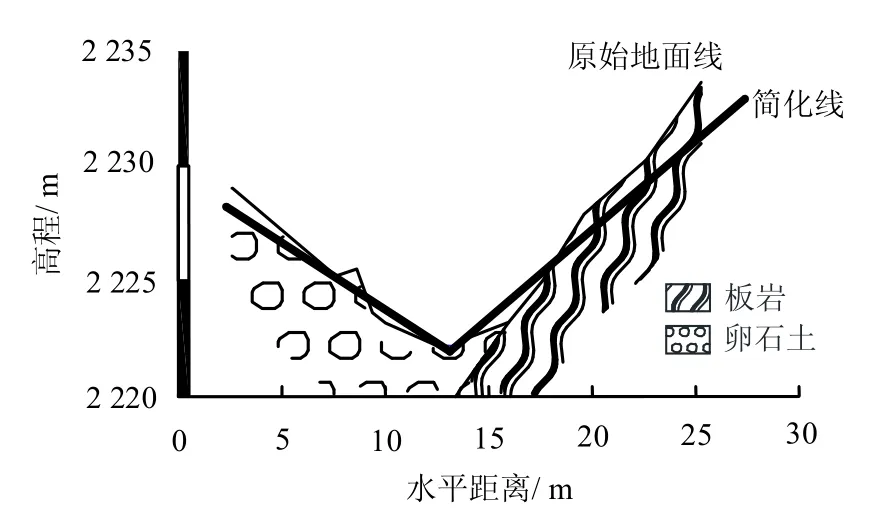
图1 V 型泥石流沟道简化图 Fig.1 Simplification of V-shaped debris flow's gully cross-section

（4）将简化后的截面横向分割成n 个小过流面（见图2），假设断面的总流量等于n 个梯形过流量之和，即：

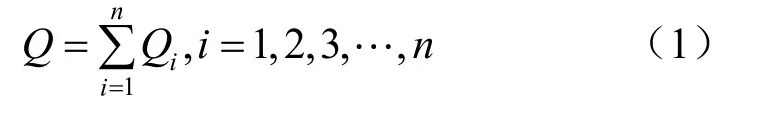
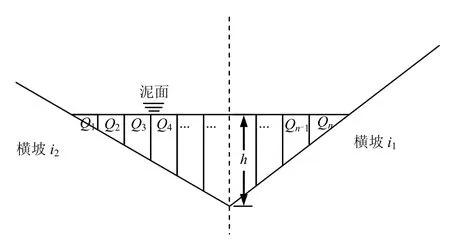
图2 沟道横断面的有限分割 Fig.2 Finite partition of debris flow's gully cross-section

假设（1）适用于泥石流流通区，不适用于形成区与堆积区等冲淤不平衡断面。假设（2）适用于流通区非沟道转弯处的断面流速计算，假设（3）、（4）则对沟道几何形态进行了适当简化，方便了数学模型的建立。

2.2 基本流速公式选取

目前，国内外确定泥石流流速的方法很多，得出的计算公式不下数10 种，绝大部分公式形式为[8]

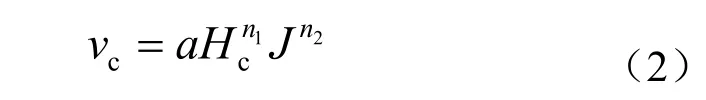
式中：cH 为泥石流过流断面的水力半径，一般用泥痕深度代替；J 为泥石流沟床的比降；1n 、2n 为指数常数，不同公式有不同值；a 为参数，一般与泥石流重度、颗粒组成、泥痕深度、坡降以及沟床粗糙程度有关。

由式2 可知，在同一断面流速仅随泥深变化，考虑流速公式的适用性，本文选取文献[17]的流速公式进行计算。

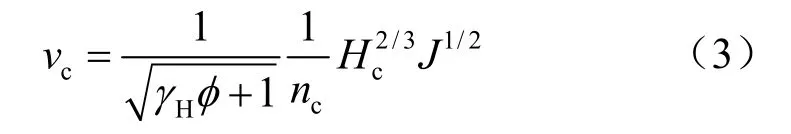
式中：Hγ 为固体物质重度（kN/m3）；cn 为泥石流沟床的糙率系数；φ 为泥石流泥砂修正系数（见表1）。

3 流速及荷载横向分布

3.1 流速横向分布计算

以沟道简化后的V 型折线底边点为原点，可建立相应的坐标体系（见图3），由形态断面法可得

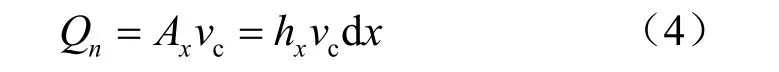
代入式（1）可得

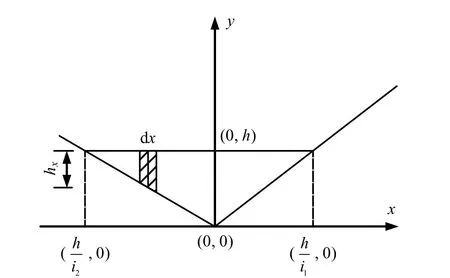
图3 相应坐标体系的建立 Fig.3 Establishment of the corresponding coordinate

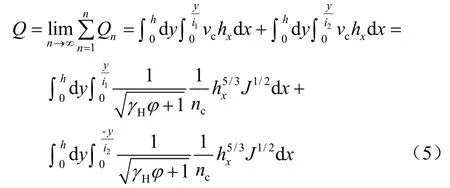
式中：x 为距最低点距离（m）；xh 为距最低点x 处的泥深（m），由式（6）确定；h 为沟道中心泥深（m）；1i 、2i 分别为右端、左端沟道简化线横坡（%）；其余符号同前。

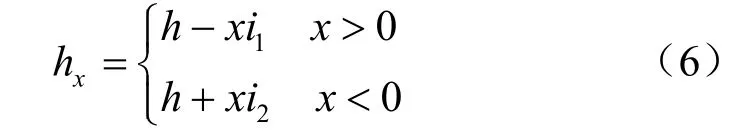
将式（6）代入式（5）中积分可得

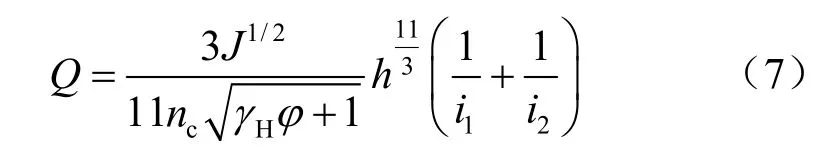
式（7）表明，h 是关于i、J、Q 的函数，这4个参数中，断面处泥石流流量Q可采用雨洪法计算，纵坡J 与沟道左右岸的比降1i 、2i 可以直接测量出，因此，就可以求出h，最后把h 代入式（6）可求出xh ，把xh 代入式（3），可得到与沟道最低点距离x处的任意位置的流速横向分布计算公式：

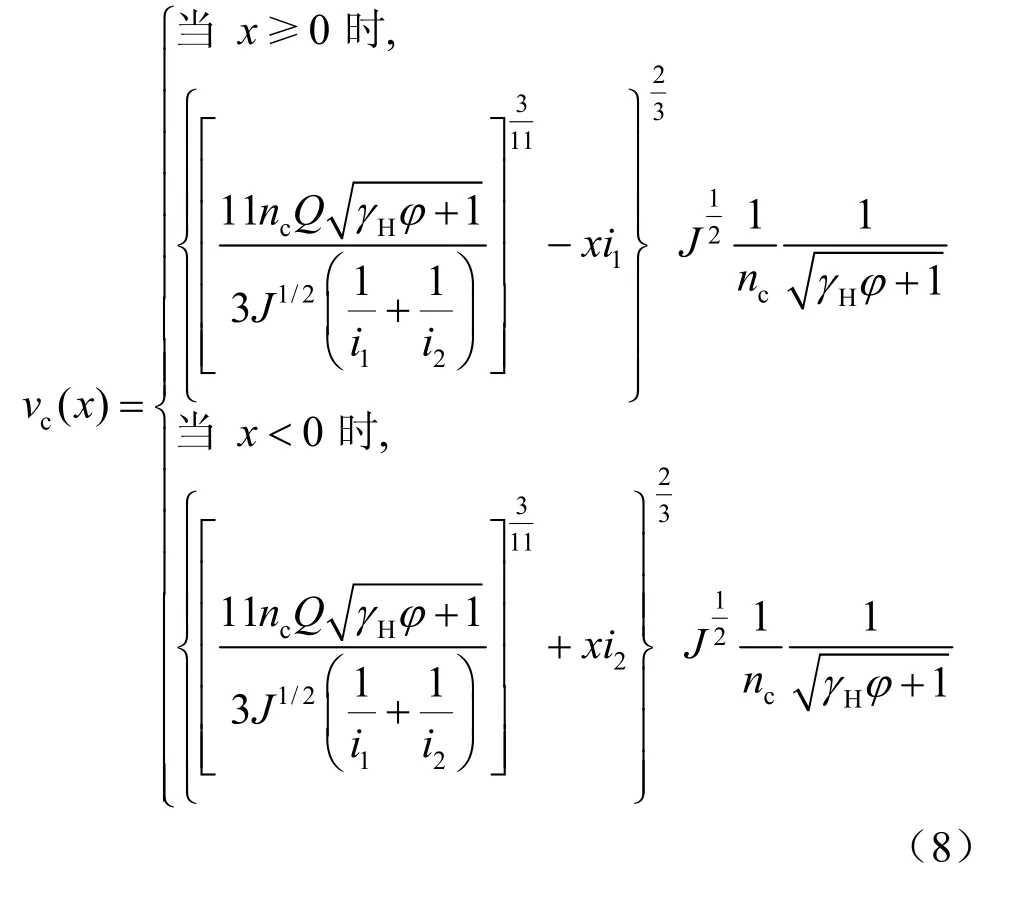
式（8）表明，泥石流流速与横向截面位置x 有关。当 x= 0时，泥石流流速最大，而随着的增大流速递减，即泥石流流速在横向上呈现出中间 大、两侧小的非线性分布特点，这一特点与康志成等[14－15]东川蒋家沟泥石流现场观测到的龙头特点（平面上的位置是一个向前突出的舌形体）并判断与泥石流表面流速中间大、两侧小的结果基本吻合。

3.2 泥石流冲击荷载横向分布

泥石流冲击荷载主要包括泥石流整体冲压力Fδ、泥石流中大块石的冲击力bF 以及泥石流动水压力σ ，其计算公式如下所示。

（1）泥石流整体冲击力[17]：

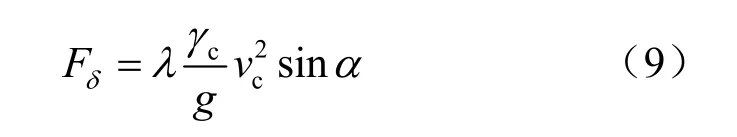
（2）泥石流块石冲击力[18]：

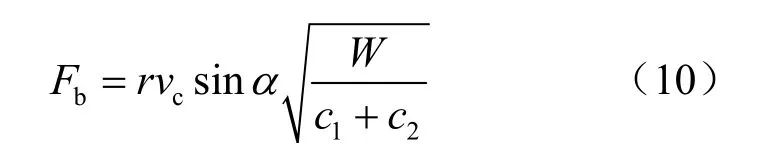
（3）泥石流动水压力[17]：

式中：Fδ为泥石流整体冲击压力（kPa）； Fb为泥石流大块石冲击力（kN）；σ 为泥石流动水压力（kPa）；γc为泥石流重度（kN/m3）； vc为泥石流流速（m/s）；g 为重力加速度，g=9.8 m/s2；α 为建筑物受力面与泥石流冲压方向的夹角（°）；λ 为建筑物形状系数，圆形建筑物λ =1.0，矩形建筑物λ=1.33，方形建筑物λ=1.47；r 为动能折减系数，圆端正面撞击取0.3；W 为石块重量（kg）； c1、 c2为块石与桥墩圬工的弹性变形系数 c1+ c2=0.005。

式（9）～（11）表明，泥石流荷载的分布主要受泥石流的流速分布控制，通过式（8）可以计算出沟道横截面上距离沟道最低点x 处的任意位置的流速cv 的分布情况，进而将计算出的流速cv 的分布情况代入式（9）～（11）中，可以获取泥石流荷载的横向分布情况，为泥石流防治工程的设计提供参考。

4 实例应用

本文以在建的四川理县地震灾区理县甲司口小沟泥石流应急治理工程为例，选取了一典型的V型沟道断面，分析计算了沟道内横向上的流速分布情况，确定了作用在坝体上的荷载分布情况，并在此基础上对坝体进行了优化。

4.1 研究区概况

该沟汇水面积为12.35 km2，沟道长度为7.61 km，沟床平均比降为30.9%，1984、1996 年分别发生过一次泥石流。汶川地震后，沟内新增大量松散堆积体，特别是沟道中部形成了1 座约0.63 ×1 04m3的堰塞坝，泥石流灾害危险性加剧。目前，该沟泥石流威胁的对象包括下游农户64 户227 人，建筑面积约12 000 m2，耕地300 余亩、小型电站一座，潜在直接经济损失将达到800 万元。

该沟1 号拦砂坝所在断面为一典型的V 型泥石流流通区沟道，沟道右岸基岩出露，其横剖面图见图4，泥石流在该断面位置处于冲淤平衡状态。该处纵向坡度为23.7%，经简化，左岸横向坡比为1:0.58，右岸横向坡比为1:0.77，糙率系数取8.0，附近最大块石粒径为0.8 m×0.7 m×0.5 m，泥石流重度为17.5 kN/m3，采用雨洪法计算得出坝址处断面流量为62.29 m3/s。现场调查发现，坝址处泥痕高度约为2.4 m（见图5）。

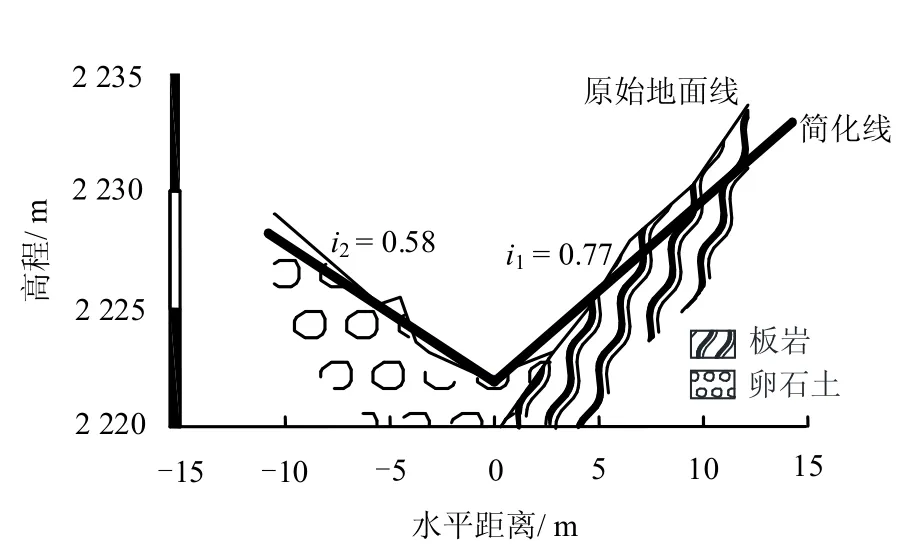
图4 甲司口泥石流沟沟道横剖面图 Fig.4 Debris flow's gully cross-section at Jiasikou debris flow valley

图5 泥石流泥痕高度调查 Fig.5 The investigation of debris flow′s mud depth

4.2 流速及荷载的横向分布计算

4.2.1 泥石流平均流速计算

采用形态断面法，应用西南地区（铁二院）公式计算平均流速：

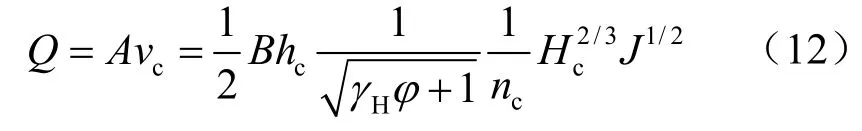
由几何关系可得

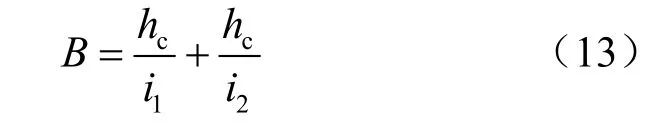
代入式（12）可得

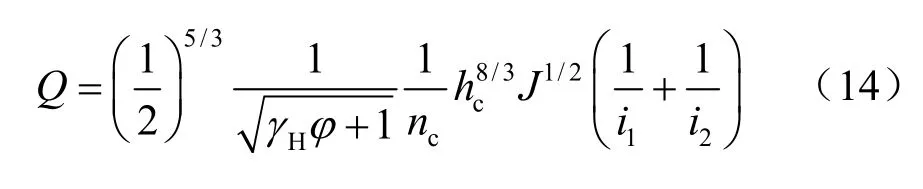
式中：B 为泥石流过流断面宽度（m）；ch 为计算断面的最大泥深（m）；cH 为计算断面的平均泥深（m），计算中取0.5ch ；参数取值如表1 所示。采用雨洪修正法计算流量Q 后可以求得最大泥深ch =3.58 m。换算成平均泥深后代入式（3），可以求得泥石流横断面的平均流速为3.20 m/s。

表1 流量与泥深关系计算表 Table 1 Relationship between discharge and mud depth of debris flow

4.2.2 泥石流流速横向分布计算

根据本文第2 节的推导过程，由流量Q 代入式（7）可以推导出泥深为2.63 m，相比平均流速所计算的泥深3.58 m，式（7）的计算结果与现场调查的泥痕深度2.4 m 更加接近，准确度更高。采用式（8）计算了沟道横剖面方向上的流速分布情况 （见图6）。

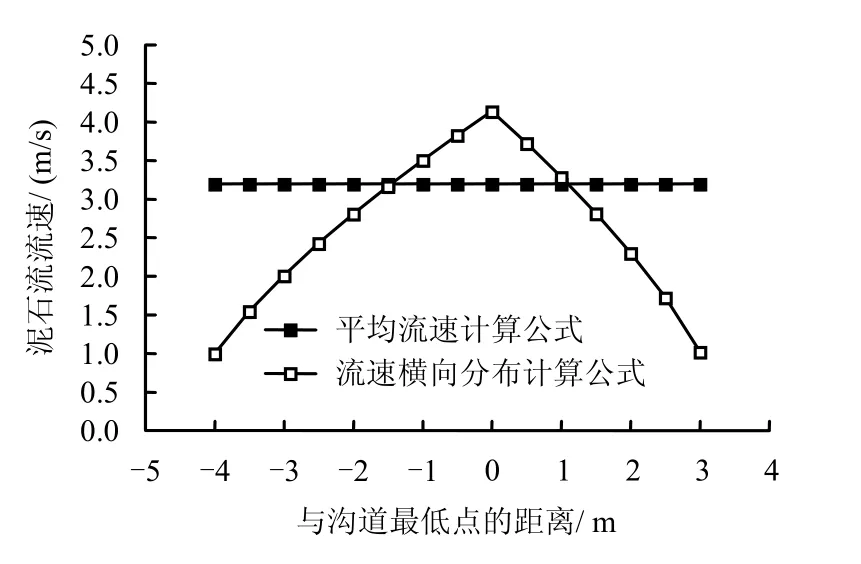
图6 泥石流流速横向分布情况与对比 Fig.6 Lateral distribution features of debris flow velocity

通过计算出拟建坝位横剖面方向上流速的分布情况后，将曲线上的各点流速带入泥石流荷载计算公式，可以得出泥石流整体冲压力、大块石冲击力以及过坝泥石流动水压力的横向分布情况（见图7）。

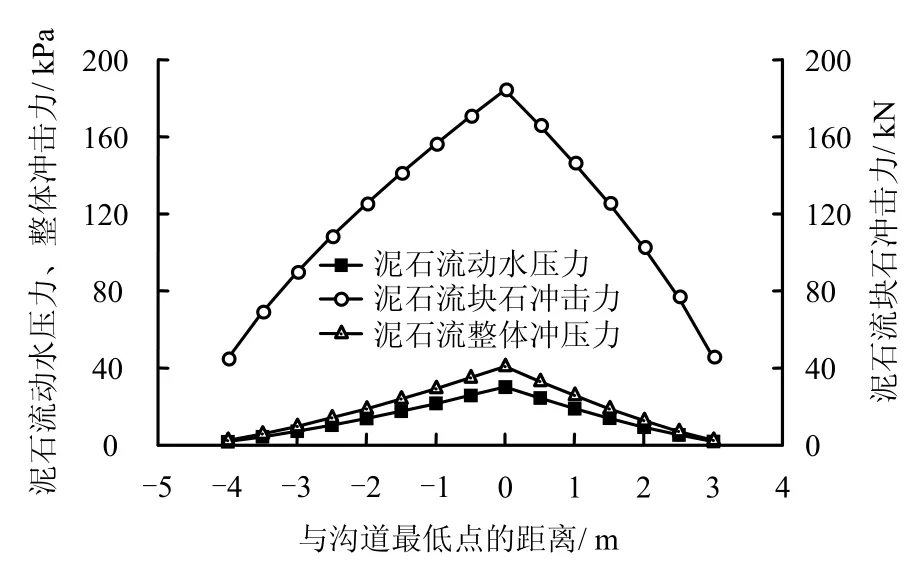
图7 泥石流冲击荷载横向分布情况 Fig.7 Lateral distribution features of debris flow impact loads

图6、7 表明，泥石流流速及泥石流拦砂坝所受荷载在沟道横剖面方向上呈非线性分布，沟道最低点处流速最大，约是坝肩两岸位置流速的4.05倍，而拦砂坝所受荷载参数与流速密切相关，也随之表现出非线性特征，并且在沟道最低点处，拦砂坝所受荷载最大。

5 泥石流防治工程结构优化建议

5.1 拦砂坝设计存在的普遍问题

以拦砂坝为例，通过上述对泥石流冲击荷载横向分布特征研究，拦砂坝最危险截面为沟道的最低点处，该处坝体承受荷载较大，在泥石流冲击作用下易使浆砌片石坝体表面的砂浆被逐渐磨蚀掉，致使坝体迎流面片石体脱离基体而被冲走，形成冲刷坑，并导致该处应力集中，破坏加剧，最终发生坝体溃决的现象（见图8）。

图8 拦砂坝中部易发生溃决 Fig.8 Breaking happens in the middle of the dam

而坝肩两侧位置流速小，所受荷载小，泥石流对其的冲击和磨蚀情况较弱，常规设计时如不考虑荷载横向分布的情况，统一按照最危险截面设计，这样就使得坝肩位置安全系数偏大，设计过于保守，并无法避免地导致工程浪费，国家资金的流失。故有必要结合流速横向分布特征，对拦挡结构进行优化。

5.2 拦砂坝结构优化思路

鉴于此，形成了重力式拦砂坝的优化思路：结合受力特点，坝体采用变截面设计，即拟设拦砂坝处横向方向上坝体断面尺寸根据所受荷载有所变化，对坝体中部泥石流荷载最大处进行加厚处理，对坝体两侧坝肩部分泥石流荷载最小处进行削弱，坝体中部加厚处与坝肩削弱处采用突变式衔接方式，即坝体厚度在横向上存在突变，俯视图上为T型。坝体中部泥石流中泓线位置的加厚区内嵌与坝体迎流面等长度的废旧钢轨或工字钢，并在表面铺设高强度混凝土，与坝基、溢流口等结构固结为一体（见图9、10）。

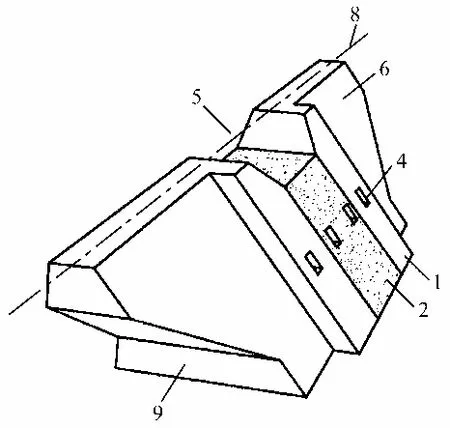
图9 拦砂坝结构优化示意图 Fig.9 Schematic of optimization of debris flow dam structure

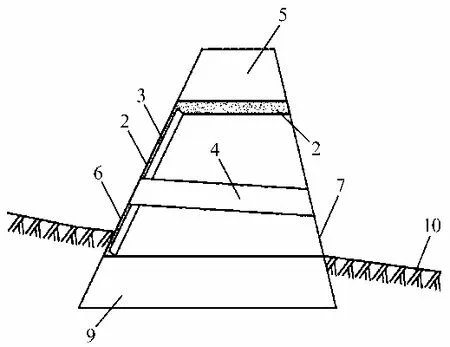
图10 拦砂坝结构优化剖面图 Fig.10 Cross-section of optimization of debris flow dam structure

图9、10 中，1 为坝体中部加厚区；2 为高强度混凝土抹面；3 为废旧钢轨或工字钢；4 为泄水孔；5 为溢流口；6 为拦砂坝迎流面；7 为拦砂坝背水面；8 为坝体中轴线；9 为坝体基础；10 为原始地面线；11 为高强度混凝土与钢轨加固区。

5.3 拦砂坝结构优化工程实例

以甲司口沟泥石流1 号拦砂坝为例（原1 号拦砂坝坝高为4 m，坝顶宽为2 m，面坡为1:0.5，背坡为1:0.2，基础埋深为2 m），对其结构设计进行了优化（见图11）：

（1）在拦砂坝最危险截面AB 段（即泥石流荷载最大处）设置坝体中部加厚区，全长为8.0 m，将坝顶宽度增加至2.2 m，面坡、背坡分别为1:0.5与1:0.2，与两侧坝肩坡度保持一致。

（2）坝体加固区CD 段全长为5.0 m，在迎流面内嵌废旧钢轨7 根，上覆厚度为30 mm 的C30 混凝土，以提高加固区抗磨蚀及抗冲击的能力。

（3）对于拦砂坝两侧坝肩设计上偏保守的位置，在满足安全稳定性的前提下进行了适当的削减，将坝顶宽减小至1.5 m，面坡、背坡分别为1:0.5 与1:0.2。 进行有限分割，运用此极限思想建立了流速横向分布的计算方法，较详细地推导了计算方法的演绎过程，获取了泥石流流速横向分布计算公式及其分布特征；

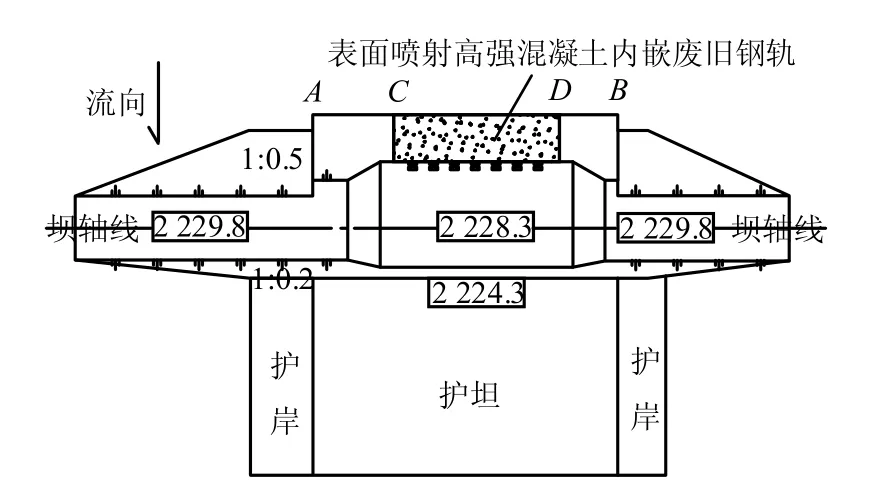
图11 甲司口沟1 号拦砂坝坝体结构优化设计图 Fig.11 Schematic of optimization of dam #1 structure at Jiasikou debris flow valley

（2）结合工程实例对获取的泥石流流速横向分布计算公式进行了验证分析，并计算了荷载的横向分布情况。计算结果表明，泥石流流速在横向上呈现出非线性分布规律，该规律与东川蒋家沟泥石流的现场监测结果具有其良好的一致性，且实例分析表明，两侧流速仅为泥石流中泓线流速的25%；

（3）基于泥石流流速及荷载的横向分布特征，以四川理县某沟在建拦砂坝为例，对坝型结构进行相应优化设计，可提高坝体的稳定性系数约20%，降低工程造价约5%；

（4）本文所推导的泥石流流速横向分布计算公式适用于V 型横断面的泥石流沟道，对于非V 型沟道，如U 型及其他不规则沟道横断面等的流速横向分布计算公式，在进一步研究中可基于本文思路，增加积分区段以获取相应的流速计算公式。

[1] 余斌. 根据泥石流沉积物计算泥石流容重的方法研究[J]. 沉积学报, 2008, 26(5): 789－796. YU Bin. Research on the calculating density by the deposit of debris flows[J]. Acta Sedimentologica Sinica, 2008, 26(5): 789－796.

[2] 徐林荣, 王磊, 苏志满. 隧道工程遭受泥石流灾害的工程易损性评价[J]. 岩土力学, 2010, 31(7): 2153－2158. XU Lin-rong, WANG Lei, SU Zhi-man. Assessment of engineering vulnerability of tunnel suffering from debris flow[J]. Rock and Soil Mechanics, 2010, 31(7): 2153－2158.

[3] 陈洪凯, 唐红梅, 马永泰, 等. 公路泥石流研究及治理[M]. 北京: 人民交通出版社, 2004: 108－121.

[4] 陈洪凯, 唐红梅, 陈野鹰. 泥石流固液分相流速计算方法研究[J]. 应用数学和力学, 2006, 27(3): 357－364. CHEN Hong-kai, TANG Hong-mei, CHEH Ye-ying. Research on method to calculate velocities of solid phase and liquid phase in debris flow[J]. Applied Mathematics and Mechanics, 2006, 27(3): 357－364.

[5] 吴积善, 田连权, 康志成, 等. 泥石流及其综合治理[M]. 北京: 科学出版社, 1993: 170－180.

（1）假设所求断面泥石流无显著淤积或物源补给，通过对泥石流沟道所求断面进行适当简化，并

5.4 工程效果及经济效益分析

优化后的坝体结构稳定性计算结果如表2 所示，对比分析可知，原设计坝体中间位置与两侧坝肩位置稳定性系数相差较大，坝体中部稳定性系数较小，为最危险截面。优化后，虽坝肩处稳定性略微减小，但坝体中部稳定性得以提高，故整体稳定性相比优化前可提高约20%，同时可节省坝体材料M10 浆砌片石约30 m3，节约工程造价8 667.46 元，占坝体工程总造价的5%左右。

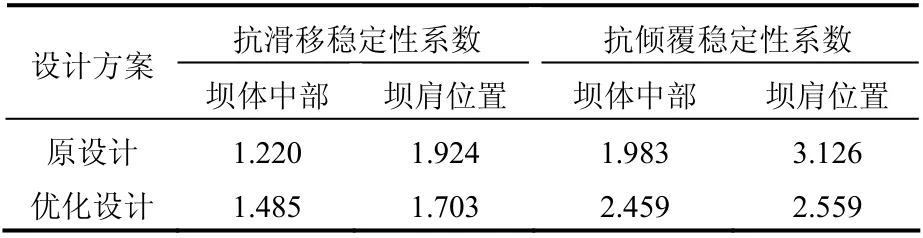
表2 优化设计前后坝体结构稳定性系数对比 Table 2 Comparison of stability coefficient of dams before and after optimization

6 结 论

[6] 吴积善, 康志成, 田连权, 等. 云南蒋家沟泥石流观测研究[M]. 北京: 科学出版社, 1990: 141－164.

[7] 周必凡. 泥石流防治指南[M]. 北京:科学出版社, 1991: 65－70.

[8] 王继康. 泥石流防治工程技术[M]. 北京: 中国铁道出版社, 1996: 61－64.

[9] KOCH T. Testing of various constitutive equations for debris flow modeling[C]//Hydrology, Water Resources and Ecology in Headwaters. Merano: IAHS Publ., 1998.

[10] TAKAHASI T, SAWADA T, SUWA H, et al. IAHR monography series[C]. The Netherlands: Balkema Publishers, 1991.

[11] PWRI, Technical standard for measures against debris flow (Draft)[M]. [S. l.]: [s. n.], 1988:48.

[12] RICKENMANN D. Debris flows 1987 in Switzerland: Modelling and sediment transport[C]//Proceedings of Two Lausanne symposia. [S. l.]: RIAHS Publisher, 1990.

[13] 韦方强, 胡凯衡. 泥石流流速研究现状与发展方向[J].山地学报, 2009, 27(9): 545－550. WEI Fang-qiang, HU Kai-heng. Review and trends on debris flow velocity research[J]. Journal of Mountain Science, 2009, 27(9): 545－550.

[14] 康志成, 李焯芬, 马蔼乃, 等. 中国泥石流研究[M]. 北京: 科学出版社, 2004: 159－162.

[15] 康志成. 云南东川蒋家沟黏性泥石流流速分析[C]//中国科学院兰州冰川冻土研究所集刊(4). 北京: 科学出版社, 1984: 108－118.

[16] TECCA P R, DEGANUTTI A M, GENEVOIS R, et al. Velocity distributions in a coarse debris flow[C]// RICKENMANN D, CHEN C. Debris flow Hazards Mitigation: Mechanics, Prediction, and Assessment. Rotterdam: [s. n.], 2003: 905－916.

[17] 中华人民共和国国土资源部. DZ－T0239－2004 泥石流灾害防治工程设计规范[S]. 北京: 中华人民共和国国土资源部, 2006.

[18] 王继康. 泥石流防治工程技术[M]. 北京: 中国铁道出版社, 1996: 80－81.