决定饱和岩土材料变形的有效应力及孔压系数
陈晶晶 ,雷国辉
(1.河海大学 岩土力学与堤坝工程教育部重点实验室,南京 210098;2.河海大学 岩土工程科学研究所,南京 210098; 3.铁道第三勘察设计院集团有限公司地质路基设计处,天津 300251)
1 引 言
有效应力原理是将岩土材料多相(孔)介质应力状态简化为单相介质应力状态,以便于运用连续介质力学解决岩土材料变形和强度问题的一种固体力学或热动力学等效方法[1-4],如图1 所示。有效应力是决定岩土材料变形和强度的应力状态变量或其组合。有效应力表达式给出了有效应力与应力变量(比如总应力和孔压等)之间的关系,取决于是变形等效还是强度等效[1,5-8]。
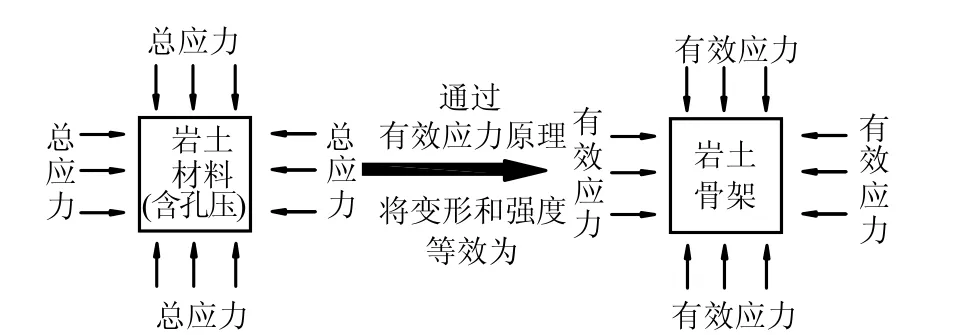
图1 有效应力原理示意图 Fig.1 Schematic diagram of the principle of effective stress
对于饱和岩土材料,雷国辉等[1]已从强度等效的角度,运用摩擦学中的黏着摩擦理论,分析了其有效应力的表达式。本文则从变形等效的角度,分析饱和岩土材料的有效应力表达式,同时,也分析了Skempton[9]的孔压系数B 的表达式。
2 既有研究成果的历史回顾与评述
2.1 有效应力表达式
De Boer 等[10]追溯了有效应力概念从萌芽到成形阶段的历史进程。虽然在Terzaghi 之前,一些学者通过试验研究已经发现了饱和岩土材料中的孔压对其变形和强度特性的某些影响机制[5-6,10],但Terzaghi 被公认为是有效应力概念的创始人已是不争的事实。早在1923 年,他就应用了有效应力的概念建立了一维固结理论[11]。在1936 年第1 届土力学与基础工程国际会议上,他创造性地提出了有效应力一词[12],明确地定义了有效应力表达式:

式中:σ′为法向有效应力;σ 为法向总应力;u 为孔压。而且更为重要的是,他清晰地赋予了其内涵,即岩土材料的压缩、变形和抗剪强度由有效应力所决定[12]。与 σ = σ′+ u的书写形式相比,式(1)能够更好地体现出有效应力原理和有效应力概念的内涵。虽然Terzaghi 当时并未给出表达式(1)的理论证明,但有效应力概念自此已成为现代岩土力学的里程碑和奠基石。
在强度等效方面,式(1)普遍适用于岩石、混凝土、土(除高塑性黏土[13]尚未有定论外)等饱和岩土材料[1]。不过,在变形等效方面,理论和试验研究成果已经证明[5-6,10,14-16],式(1)并不适用于所有岩土材料,只有当固相和非黏性液相[10]的压缩性与骨架的压缩性相比可以认为是不可压缩时式(1)才适用。
在为数不少的土力学教材中,有效应力常常被理解为是单位土体截面积上的粒间接触力,其表达式为

式中:sN 为作用在粒间的法向接触力;N 为作用在土体的法向力;A 为土体的截面积;sA 为相应土粒间的接触面积;a 为粒间接触面积比,即粒间接触面积与土体截面积的比值。而式(1)也常常被理解为是式(2)当粒间接触面积比a 可忽略不计时的特例。
值得注意的是,式(2)中的σ ′= Ns/A 并不是单位粒间接触面积上的粒间接触力 Ns/As,即,不是真实的粒间接触应力,而是与渗流问题中的假想平均流速类似的假想粒间接触应力。幸运的是,假想平均流速因Darcy 定律而具有其存在意义;但假想粒间接触应力至今却未发现其存在价值。Singh等[17]通过力学分析推导了真实的粒间接触应力,其算例分析显示,如果粒间接触面积比a 可忽略不计的话,真实的粒间接触应力则要比假想的粒间接触应力大得多。当然,这也是预料之中的结果。
另外,Bishop 等[18]的理论分析和三轴不排水试验结果、Skempton[5]的高压固结试验和三轴压缩试验结果、以及Bishop 等[19]的三轴排水试验结果,均已证明,式(2)不是决定饱和岩土材料变形和强度的有效应力。
更为重要的是,无论是假想的粒间接触应力 (式(2)),还是真实的粒间接触应力(比如:文献[17]),仅仅在力的平衡基础上推导的,并没有体现有效应力原理和有效应力概念的真正内涵,即没有体现是强度等效或是变形等效、没有体现岩土材料的压缩、变形和抗剪强度由有效应力所决定。
而更为令人可惜的是,Lade 等[6]通过文献检索到的另外2 种有效应力表达式:σ ′= σ- nu( 由n= 1 - a代入式(2)得到,其中n 为孔隙率)及σ ′= σ- η u(其中 n ≤η ≤ 1),以及李广信[20]和陈愈炯[21]列举批评的其他形式的有效应力表达式,如基于所谓的水压率概念得到的 σ′ = (σ - nu )/(1 - n),甚至只是凭直觉构造的[6]或是在错误的理解和推导基础上得到的有效应力[20-21]。
真正从变形等效的角度、通过理论分析来推导有效应力的表达式并不多见。研究的思路主要是通过在假设材料内部孔隙连通(相应的孔隙率n 为有效孔隙率)的基础上,将不排水条件下围压(总应力)与孔压作用引起饱和岩土材料固相和液相的压缩导致的骨架体积变形,等效为排水条件下围压(有效应力)作用引起饱和岩土材料的骨架体积变形,建立两者之间的等效关系,以推求得到有效应力的表达式。之所以选择体积变形而非剪切变形或形状变形,是由于一般的饱和岩土材料中的非黏性液相不能承受剪应力且孔压不影响土骨架的剪切变形。
按照上述思路,Skempton[5]、Nur 等[22]、Bishop[23]通过理论分析和试验验证得到了一致的有效应力表达式[6]。其中,Bishop 的理论分析相对简洁且最为详细。分析中隐含定义了液相的体积压缩系数wC 、固相的本征体积压缩系数gC 以及排水条件下骨架的体积压缩系数skC ,如下:

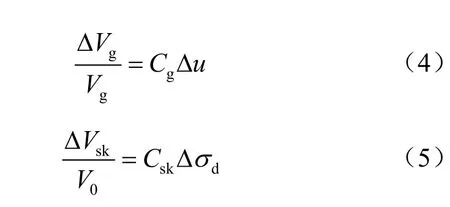
式中:wV 、gV 和0V 分别为饱和岩土材料液相、固相和骨架的体积; VΔ 为体积增量; uΔ 为孔压增量;σΔ 为围压增量,下标w、g、sk 和d 分别表示液相、固相、骨架和排水条件。
按照上述定义,Bishop[23]分析了不排水条件下受到围压增量 σΔ 作用时,分别由如图2 中等号右边所示的孔压增量 uΔ 作用和常孔压、净围压增量( σΔ - )uΔ 作用引起的液相、固相和骨架的体积增量,如表1 第3 列所示,其中:下标u 和s 分别表示孔压增量 uΔ 和净围压增量( )uσΔ -Δ 作用。

图2 围压与孔压作用的分析 Fig.2 Analysis of the actions of cell pressure and pore pressure
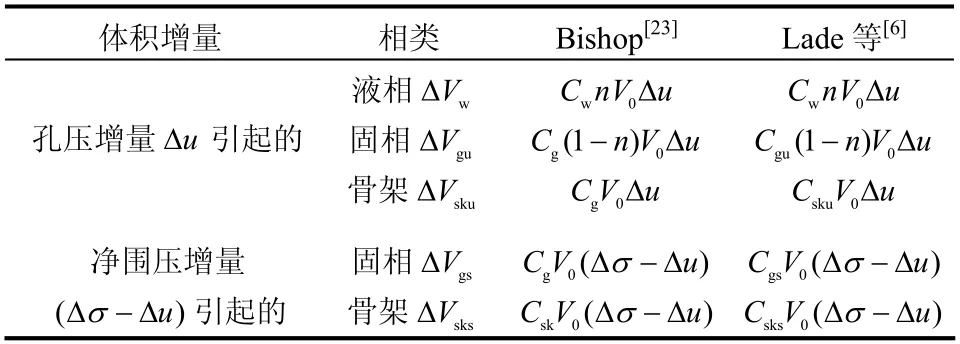
表1 Bishop[23]、Lade 等[6]对变形的分析 Table 1 Deformation analysis by Bishop[23], Lade and de Boer[6]
表1第3列中的 wVΔ 、guVΔ 和 sksVΔ 值由式(3)~(5)直接确定。对于 skuVΔ 值,Bishop[23]认为,孔压增量引起的骨架体积应变与孔压增量引起的固相体积应变相等,因此,有
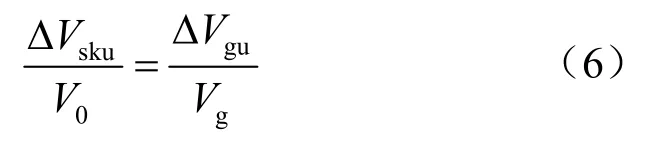
则有
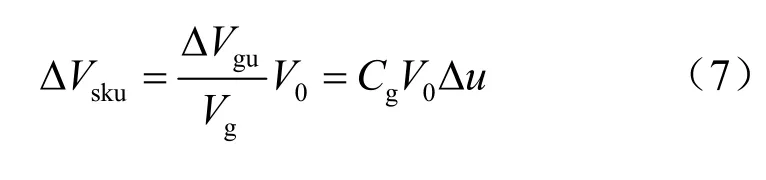
另外,对于 gsVΔ 值,他假设孔隙随机分布,则面积孔隙率与体积孔隙率相等(其数学证明可参见文献[24-25]),因此,固相的接触面积占骨架截面面积的比值 a = (1 - n),当骨架受到净围压增量作用时,施加在固相上的平均球应力增量为( Δσ - Δu )/ (1 - n),它所引起的固相体积增量为
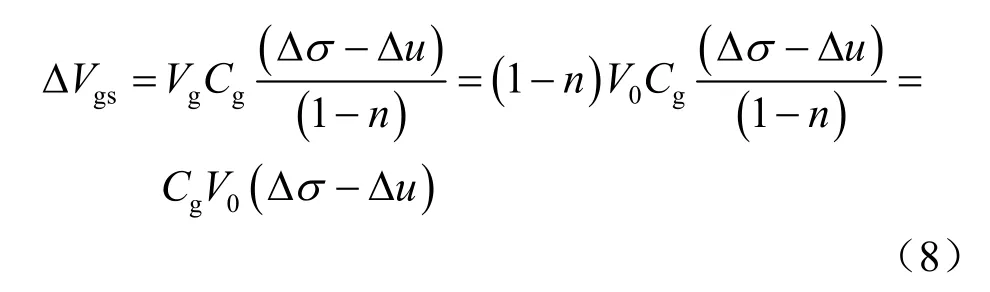
按照不排水条件下在总应力和孔压作用下的骨架变形,即孔压增量和净围压增量引起的骨架体积增量之和(如图2 所示),与排水条件下在有效应力作用下的骨架变形等效,即变形等效的原则,可得
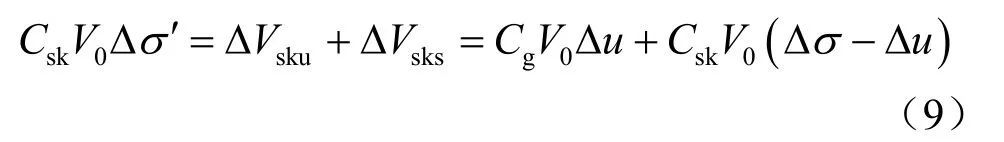
因此,Bishop[23]得到的有效应力表达式为
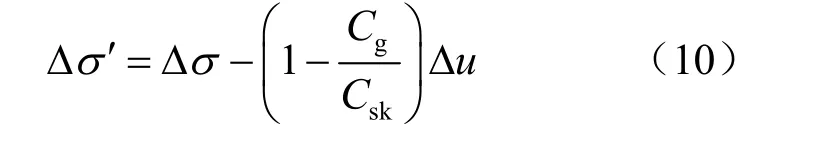
Lade 等[6]则为区别孔压增量和净围压增量作用引起的体积增量而定义了相应的固相体积压缩系数Cgu和 Cgs,以及相应的骨架体积压缩系数 Csku和Csks,其表达式为
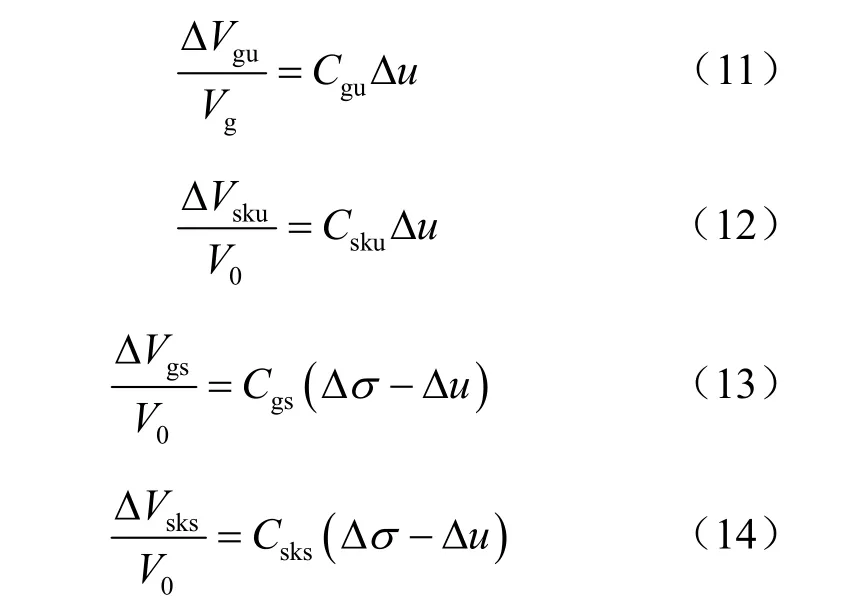
按照上述定义,Lade 等[6]分析了不排水条件下在围压增量 σΔ 作用下分别由孔压增量 uΔ 和净围压增量( )uσΔ -Δ 引起的液相、固相和骨架的体积增量,如表1 第4 列所示。
按照变形等效的原则:
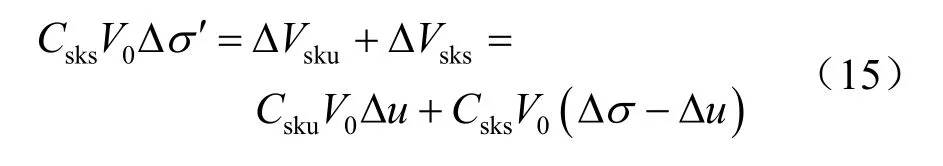
因此,其一般形式的有效应力表达式为

对于粒类土,Lade 等[6]引用前述Bishop[23]的 “孔压增量引起的骨架体积应变与孔压增量引起的固相体积应变相等”(即式(6))的观点,但错误地将应变相等理解为体积增量相等,即认为

由式(11)、(12)得

代入式(16)得到粒类土的有效应力表达式为
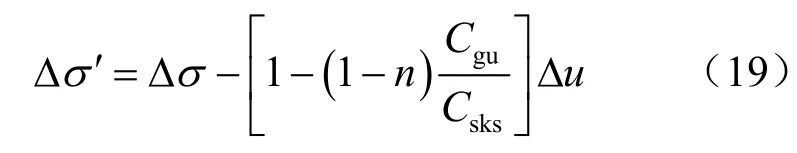
对于坚硬岩石,Lade 等[6]认为, Csku= Cgu,得到其有效应力表达式为
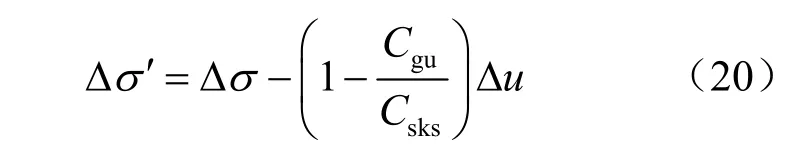
2.2 孔压系数B 的表达式
上述关于液相、固相和骨架的变形分析不仅为推求有效应力表达式提供了依据,也为推求Skempton[9]定义的不排水条件下围压作用引起饱和岩土材料的孔压系数B 值( B =Δu /Δσ )提供了依据。
按照骨架体积增量与固相和液相的体积增量之和相等的原则,即

根据表1,Bishop[23]推求的孔压系数B 的表达式为

Lade 等[6]推求的孔压系数B 的表达式为

2.3 存在的问题
对比Lade 等[6]与Bishop[23]的分析方法可知,对于液相的体积压缩系数 Cw和净围压增量作用下骨架的体积压缩系数 Csks和 Csk,他们的定义是相同的。但前者认为,孔压增量引起的固相体积压缩系数 Cgu、孔压增量引起的骨架体积压缩系数 Csku、净围压增量引起的固相体积压缩系数 Cgs这3 个变形特性参数大小不等,而后者则认为, Cgu= Csku= Cgs并统一表示为 Cg。不过,两者对于液相、固相和骨架变形分析的基本原理是完全一致的,因为:若将 Cgu= Csku= Cgs统一表示为 Cg并代入式(16)、(23),将得到与式(10)、(22)完全相同的结果。问题在于 Cgu、 Csku、 Cgs之间到底有没有联系、有什么联系?
3 固相与骨架的压缩系数及其关系
3.1 关于Csku 与Cgu
Bishop[23]认为,孔压增量引起的骨架体积应变与孔压增量引起的固相体积应变相等,因此,由式(6)可得式(7)。类似地,根据这一观点,按照Lade 等[6]对孔压增量作用下的固相和骨架体积压缩系数的定义,即式(11)、(12),则应很容易推求得到 Csku= Cgu,而非式(18)。为澄清这一观点,以下给出了 Csku= Cgu的具体证明过程。
假设有如图3 所示的模拟孔压增量对固相和骨架变形影响的试验装置,试样1~3 是由相同固相颗粒材料组合构成的不同骨架,其中试样2 颗粒间点点接触,试样3 颗粒间存在一定的接触面积。施加荷载使得装置中的孔压发生变化,试样中颗粒的受力情况可分为两种情况,如图4 所示。
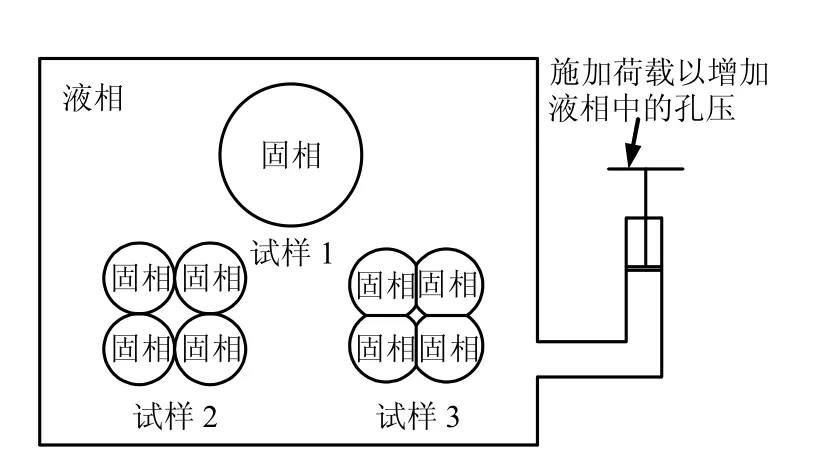
图3 假想试样和试验示意图 Fig.3 Schematic diagram of hypothetical specimens and testing
首先,对孔压作用下试样1、2 的圆形颗粒进行受力分析,如图5 所示,取其中任意一个截面为研究对象,设此截面对应的圆心张角大小为φ,则圆弧面承受的孔压的合力的大小为
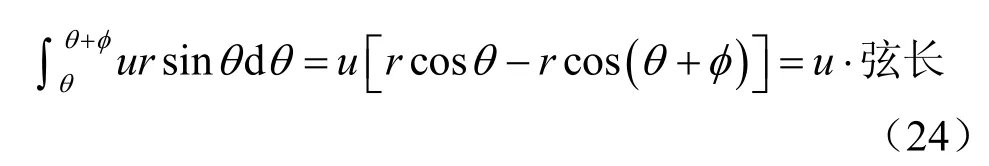
从上式可以看出,孔压作用下试样1 和2 的固相颗粒内部任意截面处只有正应力作用,大小等于孔压。
试样3 中固相颗粒的受力分析如图6(a)所示,划分截面AE 和AB 得到图6(b)所示的脱离体。通过上述图5 中圆形颗粒的力学分析可知,该脱离体上的应力分布如图6 所示,则 ulAB= σslDE+ ulCDcosθ,其中:l 为其下标所指代线段的长度; σs为粒间的接触应力。因为 lAB= lDE+ lCDcosθ,所以 σs= u,即粒间的接触应力与孔压相等。因此,与试样1、2一样,试样3 中颗粒内任意点任意方向也只承受正应力作用,大小等于孔压。

图5 圆形颗粒及其脱离体受力示意图 Fig.5 Force diagram of circular grain and its free body
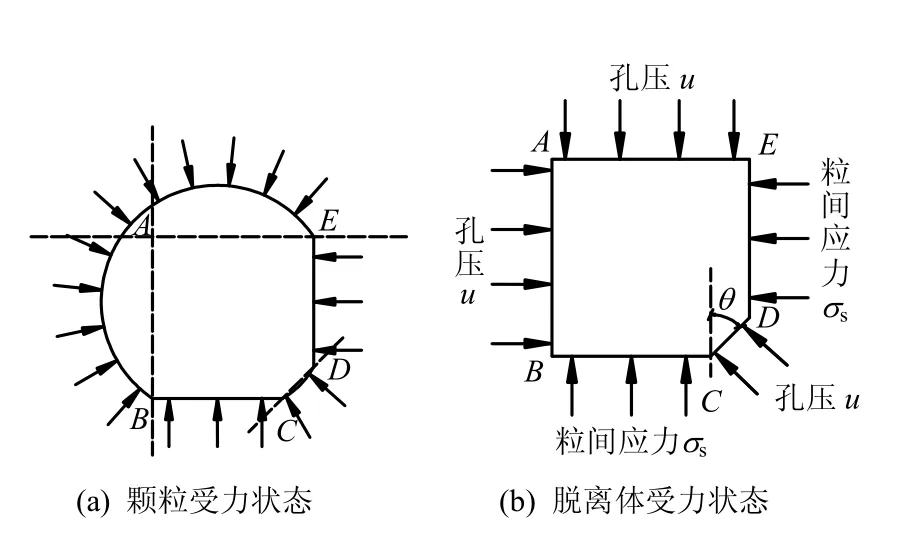
图6 试样3 中颗粒及其脱离体受力示意图 Fig.6 Force diagram of grain and its free body of specimen 3
将上述分析推广到一般情况可知,无论固相颗粒以什么样的形式构成骨架,在孔压作用下,固相颗粒内部的应力与液相内部孔压的分布规律一样,点点相同,各向同性且大小相等。
现分析孔压增加后固相颗粒变形和骨架变形之间的联系。由于试样内部任意点、任意方向的应力相等,所以应变分量也相等。这里取图2 中的试样2 为例,如图7 所示,则有

即固相颗粒的应变分量与骨架的应变分量相等。正因为如此,固相颗粒的体积应变与骨架的体积应变也相等。因此,孔压增量作用下,骨架的体积变形系数与固相的本征体积变形系数相等,即

在这一点上,Bishop[23]的分析是合理的,而Lade 等[6]的分析是错误的。
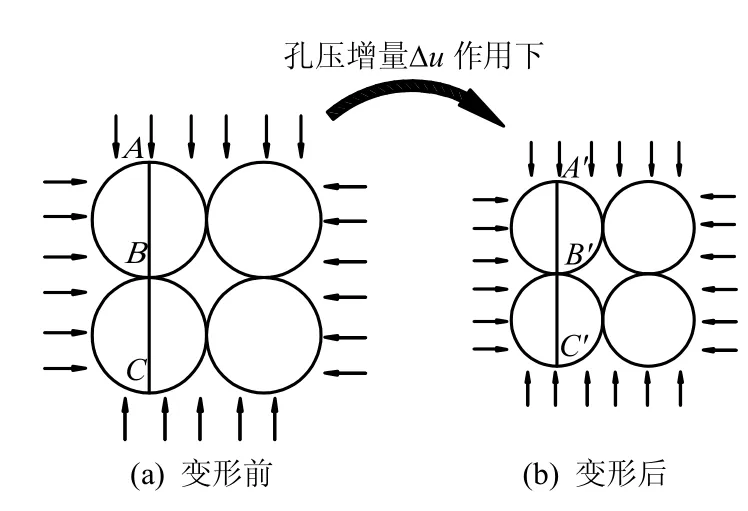
图7 孔压作用下固相和骨架的变形 Fig.7 Solid and skeleton deformations under pore pressure
3.2 关于Cgs 与Cgu
Bishop[23]没有区分净围压增量作用下固相的体积压缩系数与孔压增量作用下固相的体积压缩系数。由式(8)的推导过程及其假设可知,实际上,他认为 Cgs= Cgu= Cg。而由式(4)、(11)可知,Cgu或 Cg所表示的是在静液压力作用下固相材料的本征体积压缩系数。由图3~6 的分析可知,在静液压力作用下,固相颗粒内部的应力以及粒间接触应力均等于静液压力,即,只有正应力的作用,而没有任何剪应力的作用。但在常孔压、净围压增量作用下,净围压增量是作用在土骨架的周围(如图8 所示),而非像图3~6 那样直接地、均匀地作用在固相颗粒的周围。此时,净围压增量只作用在固相颗粒的一部分表面上,固相颗粒的受力情形与孔压作用时的受力情形是不一致的,如图9 所示。因此,固相颗粒内部以及粒间接触应力除了有正应力作用外,还有剪应力作用,固相颗粒的体积变形是这两种应力作用的结果。很显然,净围压增量作用下固 相的体积压缩系数与孔压增量作用下固相的体积压缩系数并不会相等,即 Cgs≠ Cgu,除非固相材料不具有剪胀或剪缩性。因此,在这一点上,Lade 等[6]的分析是合理的,而Bishop[23]的分析是粗略的。
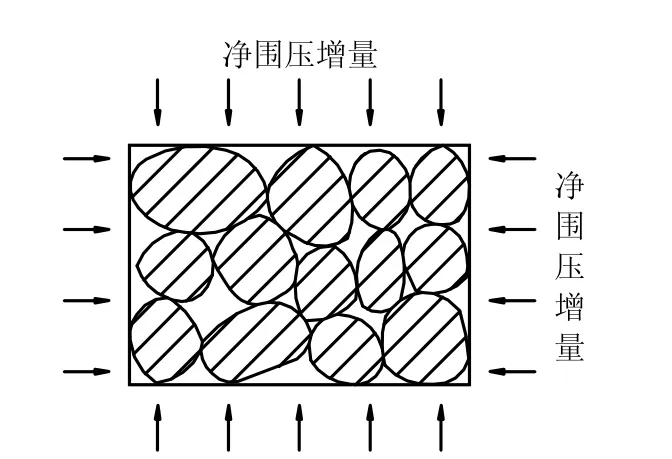
图8 净围压增量作用在土骨架周围 Fig.8 Increment of net cell pressure on the skeleton
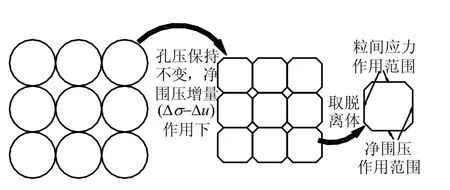
图9 净围压增量引起的固相和骨架变形 Fig.9 Solid and skeleton deformations under increment net cell pressure
4 不排水条件下围压作用的体积变形
通过上节分析,则可以列出不排水条件下分别由孔压和净围压增量引起的液相、固相和骨架的体积增量(如表2 所示)。

表2 本文的体积变形分析 Table 2 Volumetric deformation analysis of this paper
5 有效应力与孔压系数B 的表达式
按照不排水条件下在总应力和孔压作用下的骨架变形,即孔压增量和净围压增量引起的骨架体积增量之和(如图2 所示),与排水条件下在有效应力作用下的骨架变形等效,即变形等效的原则,由表2 可得
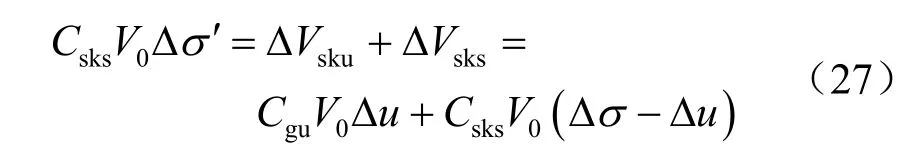
因此,决定饱和岩土材料变形的有效应力表达式为
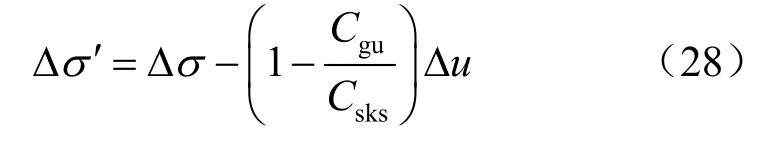
另外,按照骨架体积增量与固相和液相的体积增量之和相等的原则,将表2 中的各项代入式(21),可得到孔压系数B 的表达式为

6 讨 论
6.1 决定变形与决定强度的有效应力表达式
Skempton[5]给出了不同岩土材料的 Cgu和 Csks值,代入式(28)可知:对于饱和砂与土,1 -Cgu/Csks值近似等于1,决定变形与决定强度[1]的有效应力表达式(1)基本一致,在分析其应力-变形-强度关系时,式(1)是适用的;而对于饱和岩石与混凝土,式(28)与式(1)则有明显的差别,比如,石英质砂岩的 1 - Cgu/Csks值仅为0.54。Nur 等[22]基于砂岩和花岗岩的试验结果已经证明了式(28)的有效性。在饱和岩石与混凝土材料向着临界状态发展达到其抗剪强度的过程中,式(28)如何与式(1)趋于一致还有待于进一步的研究。
6.2 关于孔压系数B
Lade 等[6]认为,Bishop 的孔压系数B 的表达式(22)存在 B > 1的问题,即当 Cg> Cw时,式(22)给出的 B > 1。他们采用白塞木、椴木、聚丙烯塑料这3 种材料(满足 Cg> Cw)开展了室内试验,证实了B 不大于1。他们因此而认定式(22)是不正确的。如若真是这样的话,本文所提出的表达式(29)也将是错误的。
事实上,当 Cg> Cw即本文中 Cgu> Cw时,这意味着固相的压缩性大于液相的压缩性,此时,材料抵抗外力作用而产生变形的骨架已不再是由其固相所构成,液相则构成材料抵抗外力作用而产生变形的“骨架”,如图10 所示。

图10 围压引起液相骨架的变形 Fig.10 Deformation of liquid phase skeleton under cell pressure
在这种情况下,固相就好比是悬浮于液相骨架之中。由于液相与固相不同,具有可流动性以及静止时孔压传递的等值性(即Pascal 定律),因此,在围压作用下,液相骨架将承担围压荷载并等值传递给固相,材料的内部将不存在任何剪应力的作用。毋庸置疑的是,若排除围压作用边界上液相和固相的包裹材料的变形约束影响,孔压将等于围压,孔压系数B ≡ 1。而Lade 等[6]针对3 种gwC C> 材料得到B 接近于1 但非B=1 的试验结果,其根本原因除了他们自己坦承的试验精度较差外,还在于其试验过程中,在橡皮膜内立方体试样的四周放置了 1 mm 厚不锈钢板所产生的变形约束作用。
对于绝大多数的岩土材料,其 Cgu值[5-6]一般介于(1~ 3) ×10-8kPa-1之间,水的 Cw值[6]约为48× 10-8kPa-1,即 Cgu< Cw,因此,式(29)是适用的。
7 结 论
(1)孔压增量作用下,骨架的体积压缩系数与固相材料的本征体积压缩系数相等。在这一点上,Lade 等[6]的分析不合理。
(2)净围压增量作用下,固相的体积压缩系数并不等于孔压增量作用下固相材料的本征体积压缩系数。在这一点上,Bishop[23]的分析不合理。
(3)对于饱和砂与土,由于固相的本征体积压缩系数远小于净围压增量作用下骨架的体积压缩系数,决定变形的有效应力表达式与决定强度的Terzaghi 有效应力表达式基本一致。而对于饱和岩石与混凝土,决定变形的有效应力表达式与决定强度的Terzaghi 有效应力表达式不同,会随着骨架变形的发展过程而变化,如何趋于一致还有待于进一步的研究。另外,饱和岩土材料中存在不连通孔隙时的有效应力表达式也有待于进一步的研究。
[1] 雷国辉, 陈晶晶. 有效应力决定饱和岩土材料抗剪强度的摩擦学解释[J]. 岩土工程学报, 2011, 33(10): 1517-1525. LEI Guo-hui, CHEN Jing-jing. Tribological explanation of effective stress controlling shear strength of saturated geomaterials[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1517-1525.
[2] HOULSBY G T, DEAN E T R. Discussion: editorial[J]. Géotechnique, 2005, 55(5): 415-417.
[3] NUTH M, LALOUI L. Effective stress concept in unsaturated soils: clarification and validation of a unified framework[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(7): 771-801.
[4] KHALILI N, GEISER F, BLIGHT G E. Effective stress in unsaturated soils: review with new evidence[J]. International Journal of Geomechanics, ASCE, 2004, 4(2): 115-126.
[5] SKEMPTON A W. Effective stress in soils, concrete and rocks[C]//Proceedings of the Conference on Pore Pressure and Suction in Soils. London: Butterworths, 1960: 4-16.
[6] LADE P V, DE BOER R. The concept of effective stress for soil, concrete and rock[J]. Géotechnique, 1997, 47(1): 61-78.
[7] 沈珠江. 莫把虚构当真实——岩土工程界概念混乱现象剖析[J]. 岩土工程学报, 2003, 25(6): 767-768. SHEN Zhu-jiang. No confusing fiction with reality- analysis of misunderstanding of some concepts in geo- technical engineering[J]. Chinese Journal of Geote- chnical Engineering, 2003, 25(6): 767-768.
[8] 赵成刚, 韦昌富, 蔡国庆. 土力学理论的发展和面临的挑战[J]. 岩土力学, 2011, 32(12): 3521-3540. ZHAO Cheng-gang, WEI Chang-fu, CAI Guo-qing. Development and challenge for soil mechanics[J]. Rock and Soil Mechanics, 2011, 32(12): 3521-3540.
[9] SKEMPTON A W. The pore pressure coefficients A and B[J]. Géotechnique, 1954, 4(4): 143-147.
[10] DE BOER R, EHLERS W. The development of the concept of effective stresses[J]. Acta Mechanica, Springer-Verlag, 1990, 83(1-2): 77-92.
[11] CLAYTON C R I, STEINHAGEN H M, POWRIE W. Terzaghi's theory of consolidation, and the discovery of effective stress[J]. Geotechnical Engineering, ICE, 1995, 113(4): 191-205.
[12] TERZAGHI K. The shearing resistance of saturated soils and the angle between the planes of shear[C]// Proceedings of the 1st International Conference on Soil Mechanics and Foundation Engineering. Boston: [s. n.], 1936, 1: 54-56.
[13] MITCHELL J K, SOGA K. Fundamentals of soil behavior (3rd edition)[M]. New York: John Wiley & Sons, Inc., 2005.
[14] OKA F. Validity and limits of the effective stress concept in geomechanics[J]. Mechanics of Cohesive-Frictional Materials, 1996, 1(2): 219-234.
[15] BLUHM J, DE BOER R. Effective stresses-a clarification[J]. Archive of Applied Mechanics, Springer-Verlag, 1996, 66(7): 479-492.
[16] DE BOER R. Uplift, friction, capillarity and effective stress: revisited via the porous media theory[J]. Géotechnique, 2001, 51(9): 811-814.
[17] SINGH P N, WALLENDER W W. Effective stress from force balance on submerged granular particles[J]. International Journal of Geomechanics, ASCE, 2007, 7(3): 186-193.
[18] BISHOP A W, ELDIN G. Undrained triaxial tests on saturated sands and their significance in the general theory of shear strength[J]. Géotechnique, 1950, 2(1): 13-32.
[19] BISHOP A W, SKINNER A E. The influence of high pore-water pressure on the strength of cohesionless soils[J]. Philosophical Transactions of the Royal Society of London, Series A, Mathematical and Physical Sciences, 1977, 284(1318): 91-130.
[20] 李广信. 关于有效应力原理的几个问题[J]. 岩土工程学报, 2011, 33(2): 315-320. LI Guang-xin. Some problems about principle of effective stress[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(2): 315-320.
[21] 陈愈炯. 有效应力原理对饱和黏土的适用性[J]. 岩土工程学报, 2011, 33(6): 985-988. CHEN Yu-jiong. Validity of effective stress principle in saturated clay[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(6): 985-988.
[22] NUR A, BYERLEE J D. An exact effective stress law for elastic deformation of rock with fluids[J]. Journal of Geophysical Research, 1971, 76(26): 6414-6419.
[23] BISHOP A W. The influence of an undrained change in stress on the pore pressure in porous media of low compressibility[J]. Géotechnique, 1973, 23(3): 435-442.
[24] BEAR J. Dynamics of fluids in porous media[M]. New York: American Elsevier Publishing Company, Inc., 1972.
[25] PINDER G F, GRAY W G. Essentials of multiphase flow and transport in porous media[M]. New Jersey: John Wiley & Sons, 2008.

