9 加锚岩质边坡稳定性评价的极限分析上限法

9 加锚岩质边坡稳定性评价的极限分析上限法

9.1 加锚岩质边坡极限分析上限法可行性分析

传统的边坡稳定极限分析法采用垂直条分法，这个方法没有考虑岩质边坡中存在的断层、节理和层面等不连续结构面的工程地质特征。萨尔玛博士（1979）首次提出对滑体进行斜分条的刚体极限平衡分析方法，该方法假定滑体必须破裂成可以相对滑动的块体才能发生整体移动，也就是说，滑体滑动时不仅要克服主滑面的抗剪强度，而且还要克服滑体本身的强度。该法假定沿条块侧面也达到了极限平衡，这样，通过静力平衡条件即可唯一确定边坡的稳定系数或加载系数。萨尔玛法分析节理岩体边坡稳定较为合理，因为该法考虑了滑体本身的强度，可以处理具有复杂结构面的边坡，可以根据坡体内的各类结构面来划分条块，并且不要求各条块保持垂直。但是萨尔玛法一般无法保证它的解答是精确解答的上限还是下限。

1975年，陈惠发的专著《极限分析与土体塑性》，首次在土力学的边坡稳定性评价领域引入了极限分析方法，为土质边坡稳定性分析方法做出了开创性的工作。1997年，Donald和陈祖煜又提出了通过变形协调和塑性力学上限定理求解土质边坡稳定性的计算方法，进一步推动了土质边坡稳定性极限分析方法的发展。2002年，陈祖煜教授作为黄文熙讲座的撰稿人，在岩土工程学报发表了论文《土力学经典问题的塑性力学上、下限解》，在极限分析理论框架下，就土质边坡的垂直条分法和斜条分法做了深入的研究。极限分析法中的上限定理和下限定理得到的解答为精确解答的上限和下限，因此该方法得到越来越广泛的应用。

将塑性力学的极限分析方法引入到土质边坡稳定性分析中，在学术界没有争议。但是，在岩质边坡中，极限分析方法是否适用，可能还会有不同看法。当岩质边坡发生破坏时，滑体沿某一滑裂面滑动的同时，在其内部也会产生沿陡倾角结构面的剪切破坏。实际上，在自然界中，绝大部分岩体至少存在一组或几组陡倾角的结构面（断层、节理和层面）。特别是Ⅲ，Ⅳ级结构面应引起足够的重视，因为岩质边坡剪切破坏基本沿这两级结构面发生。极限分析方法就是将材料的本构关系简化为理想的刚塑性应力-应变关系，将其应用于岩质边坡，则可以近似地认为滑裂面和陡倾结构面是塑性区，而被滑裂面和陡倾结构面分割的块体为理想刚性体。

将极限分析方法应用于岩质边坡稳定性分析评价是一种新的途径，它与传统的刚体极限平衡法有较大的区别，目前仍旧处于研究阶段。Donald和陈祖煜（1997）应用极限分析上限定理，从变形协调条件出发，通过建立优化的斜分条机动许可速度场，根据外力功率和内能耗散率相平衡的原理得到了边坡最小的稳定系数。尽管一些学者对极限分析法进行了研究并取得了一些可喜的进展，但是在极限分析法中有效反映地震作用、地下裂隙水的影响以及岩石锚索（杆）支护效应的力学分析模型还很少见。因此，笔者根据极限分析上限法的基本思想，考虑地震作用、地下裂隙水的影响以及岩石锚索（杆）的支护效应，建立了锚固岩质边坡的滑体计算模型，并通过算例，对这种方法进行了稳定性分析评价。

极限分析法是同刚体极限平衡法根本不同的新方法。这种分析方法最早由Drucker和Prager提出，是将物体的本构关系简化为理想刚塑性应力-应变关系，利用刚塑性体处于极限状态的普遍原理——上下限定理求解极限荷载的一种分析方法（龚晓南，1997）。极限分析法中的上限定理和下限定理得到的是精确解答的上限和下限。它的理论基础是塑性力学的塑性位势理论。它的最大优点在于计算中考虑了岩土材料的应力-应变关系，而且物理概念清楚，计算也较简单。

根据完全塑性土（在剪切时体积不收缩）的应力-应变关系可以推导得出结论：假定外力所做的功全部消耗在滑动面间很薄的一个塑性变形区（速度间断面），那么这层土不仅沿滑动面位移，而且还沿法线方向运动，其合成速度方向与滑面的交角为土的内摩擦角。此外，根据摩尔-库仑屈服准则相适应的相关联流动法则可得到结论：滑面上的耗散能仅为黏结力与剪切位移值的乘积。

在应用极限分析中的上限法解决岩石边坡稳定性问题时，一般假定滑体自身无内能消耗，体积没有变形，相当于刚体，滑坡时内能耗散仅产生于克服滑面（速度间断面）上的阻力。大量工程地质调查表明，地质结构面是影响岩质边坡稳定的关键因素，岩质边坡大都沿岩体中软弱结构面发生失稳破坏。在边坡滑动过程中，岩体侧向结构面将发生相对滑动，同时竖向结构面并不总是保持垂直。因此，滑坡时内能耗散不仅产生于克服滑裂面上的阻力，同时消耗于克服侧向结构面上的阻力，换言之，侧向结构面在错动时也会有内能耗散。

针对加锚岩质边坡，极限分析上限法的基本要点是：当滑动体滑动时，外力（包括自重、地震力、锚固力和裂隙水压力）所做的功率等于内力（包括滑面上和侧向结构面上的阻力）所消耗的功率。于是，可由滑体处于极限状态时两功率相等的条件（虚功率方程）求出极限荷载、临界高度稳定系数（马崇武，等，2003；肖成志，等，2005）。

9.2 加锚岩质边坡极限分析法计算模型

9.2.1 加锚岩质边坡计算模型

基于极限分析上限法的锚固岩质边坡计算模型（图9-1）（王根龙，等，2007），是将一个滑体按照滑裂面和侧向结构面离散为不同的滑体单元，然后按照极限分析法的上限定理，构建一个机动许可的速度场vi-1，vi，vi-1,i。这一模式假定边坡在发生破坏时，被底滑裂面和倾斜分界面分割的各块体为刚体，而底滑裂面和倾斜分界面为塑性区。考虑到位移协调条件要求相邻滑体单元移动不至于导致它们的重叠或分离，也就是说，相邻滑体单元的速度多边形要矢量闭合。用公式表示为

相关联流动法则要求每个iv均与底滑裂面夹角为φi，要求相邻滑体单元结构面的相对速度vi-1,i与结构面夹角为φi-1,i。根据相邻滑体单元速度矢量闭合三角形的几何关系（陈祖煜，1997），可以将式（9-1）标量化后表示为

简记为

式中：

式中：θi，θi-1和θi-1,i为速度与x轴的夹角，定义为从x负方向开始，以逆时针旋转为正，且有0≤θ≤2π。在计算mi时，当i=1，令m1=1；在计算ni-1,i时，注意i≥2。θi和θi-1的计算公式为

式中：αi，αi-1为底滑裂面与水平方向的夹角，如果底滑裂面倾向与坡向一致，则α取正值，反之则取负值。

图9-1 极限分析上限法锚固岩质边坡的滑体计算模型

图9-1所示为极限分析上限法锚固岩质边坡滑体计算模型，第i个滑体单元为上侧块体，第i-1个滑体单元为下侧块体。对于第i个滑体单元和第i-1个滑体单元间的结构面，计算θi-1,i的公式可以分为以下两种情况（陈祖煜，等，2005）。

（1） 当θi＞θi-1时，说明下侧滑体单元相对于上侧滑体单元向上移动，此时下侧滑体单元对上侧滑体单元起到了阻滑的作用，这种情况在滑坡分析中占多数。此时θi-1,i的计算公式为

（2） 当θi≤θi-1时，说明下侧滑体单元相对于上侧滑体单元向下移动，此时下侧滑体单元对上侧滑体单元不但起不到阻滑的作用，反而有了下滑的危险，这种情况在滑坡分析中占少数。此时θi-1,i的计算公式为：

式中：δi-1,i为第i-1个滑体单元和第i个滑体单元间结构面的倾角，从负y轴顺时针向负x轴转为正。

9.2.2 加锚岩质边坡的外力作用力

在计算模型中，通过对滑体单元施加水平力考虑地震作用的影响；通过对滑体单元施加垂直于底滑裂面和侧向结构面的作用力考虑地下水的影响；通过对滑体结构面施加锚固力考虑岩石锚杆的支护效应。反映在极限分析上限法锚固岩质边坡计算模型中，需要分别考虑地震作用力、裂隙水压力、锚索（杆）锚固力和自重作用力，以下对各种作用力进行分述。

1）地震作用力

地震作用在边坡上的动荷载取决于坡体上产生的最大加速度。作用于第i个滑体单元的水平地震作用力为KcWi，如图9-1（a）。Kc为水平地震系数，其大小为边坡质点最大加速度与重力加速度g的比值。地震系数的取值和场地地震烈度有关，表9-1列举了各种地震烈度的经验地震系数。

表9-1 经验地震系数Kc

2）裂隙水压力

裂隙水压力是边坡稳定性分析中必须考虑的一个重要因素。这里采取与Michalowski（1995）类似的处理方法，将裂隙水压力当作外力做功出现在虚功率平衡方程中，用来求解边坡稳定的上限解。计算滑体单元裂隙水压力（图9-2）公式为

式中：Ui为作用在第i个滑体单元底滑裂面上的水压力；Pw(i-1,i)为作用在第i-1个滑体单元和第i个滑体单元间侧向结构面上的水压力；Pw(i,i+1)为第i个滑体单元和第i+1个滑体单元间侧向结构面上的水压力；zw(i-1,i)为第i-1个滑体单元和第i个滑体单元间侧向结构面的裂隙水深；zw(i,i+1)为第i个滑体单元和第i+1个滑体单元间侧向结构面的裂隙水深；dw(i-1,i)为第i-1个滑体单元和第i个滑体单元间侧向结构面水位以下部分的长度；dw(i,i+1)为第i个滑体单元和第i+1个滑体单元间侧向结构面水位以下部分的长度。

图9-2 滑体单元裂隙水压力作用示意图

3）锚索（杆）锚固力（张强勇，等，2005）

作用在第i个滑体单元滑裂面上的锚索（杆）锚固力，如图9-1（a）所示，计算公式为

式中：Rxi，Ryi分别为第i个滑体单元滑裂面上锚索（杆）锚固力的水平、竖直分量；Rmi为第i道锚索（杆）在每延米范围内提供的锚固力；βi为第i道锚索（杆）倾角；Rmi1为第i道锚索（杆）在每延米范围内由钢筋提供的抗拉承载力；Rmi2为第i道锚索（杆）在每延米范围内抗拔承载力；ni为第i道锚索（杆）中的钢筋根数；di为第i道锚索（杆）中钢筋的直径；γs为荷载分项系数；Six为第i道锚索（杆）的水平间距；fyi为第i道锚索（杆）中钢筋抗拉强度设计值；Di为第i道锚索（杆）的锚固段直径；Σqsik为第i道锚索（杆）和岩石的摩阻力；Lia为第i道锚索（杆）在滑裂面以外的有效锚固段长度。

9.3 外力功率与内能耗散

作用于边坡计算模型（图9-1）的外力包括锚索（杆）锚固力、地震作用力和自重，同时也将裂隙水压力当作外力考虑。外力功率W外计算公式为

式中：

式中：Wanchor为锚索（杆）锚固力的水平和竖直分量在应变速度场v上的外力功率；Wseismic为地震作用力在应变速度场v上的外力功率；Wgravity为自重在应变速度场v上的外力功率；Wwater为滑裂面和侧向结构面上裂隙水压力在应变速度场v上的外力功率；φi为第i个滑体单元底滑裂面的内摩擦角；φi-1,i为第i-1个滑体单元与第i个滑体单元侧向结构面的内摩擦角；其他符号同上。

滑裂面和侧向结构面上的阻力（内力）包括剪切力和法向力，其中剪切力包括两部分，一部分为黏聚力C，如图9-1（b）所示，它是已知的；另一部分是摩擦力，其值为Ntanφ，它和法向力N一起，构成一个与滑面法线方向夹角为φ的合力P——“组合摩擦力”。这个组合摩擦力的大小通常是未知的，但它的方向是已知的，即与法线方向夹角为φ。由于塑性速度v与滑面夹角为φ，这样“组合摩擦力”P与塑性速度v正交，所以P在v上所做的功率为零。因此，在计算内力产生的内能耗散内W时，只有滑裂面和侧向结构面上的黏聚力C在应变速度场v上所产生的内能耗散率，其计算公式为

式中：

式中：Dslip为滑裂面上的黏聚力在应变速度场v上所产生的内能耗散率；Dside为侧向结构面上的黏聚力在应变速度场v上所产生的内能耗散率；ci为第i个滑体单元底滑裂面的黏聚力；ci-1,i为第i-1个滑体单元与第i个滑体单元侧向结构面的黏聚力；li为第i个滑体单元底滑裂面长度；hi-1,i为第i-1个滑体单元与第i个滑体单元侧向结构面长度。

9.4 加锚岩质边坡虚功率方程

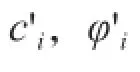
将式（9-10）、式（9-15）和式（9-18）代入虚功率方程W外=D内中，由于每个滑体单元底滑裂面的速度和滑体单元间侧向结构面的速度，均可以表达为第一个滑块速度v1的线性函数，因此可以从虚功率方程中消掉所有的速度项。整理后得到极限分析法的加锚岩质边坡稳定系数上限解表达式为（王根龙，等，2007）

式中：

公式（9-19）是稳定系数K的隐式方程，需要通过迭代的算法求解。在计算时，先假设一个初始的稳定系数K，应用迭代计算直至前后两次稳定系数K值满足所要求的计算精度为止。一般来说对于满足条件的情况，迭代都是收敛的。

当不考虑锚杆锚固力、地震力和裂隙水压力时，式（9-19）可以简化为

9.5 算例分析

图9-3所示为岩质边坡复杂平面滑动问题的标准考题（理正岩土分析软件系统默认的萨尔玛法例题），图中已标注了极限分析上限法的机动许可速度场。算例用到的基本计算参数详见表9-2，同时由表9-3给出了极限分析上限法计算速度场的结果。考虑“自重”、“自重+地震”、“自重+水”、“自重+地震+水”和“自重+锚索”五种不同的工况，采用极限分析上限法和萨尔玛法分别进行了稳定性计算，结果见表9-4。通过两种不同方法的对比分析，可以发现误差均在5%左右，显示了较好的吻合性，这就从应用上说明了极限分析上限法是解决复杂平面滑动问题的有效方法。

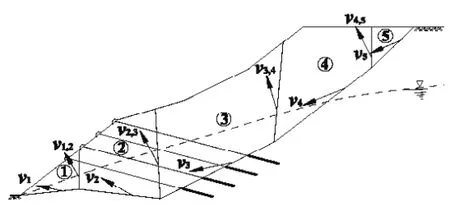
图9-3 岩质边坡的极限分析上限法工程地质剖面

表9-2 极限分析上限法稳定性计算参数

表9-3 极限分析上限法速度场计算成果

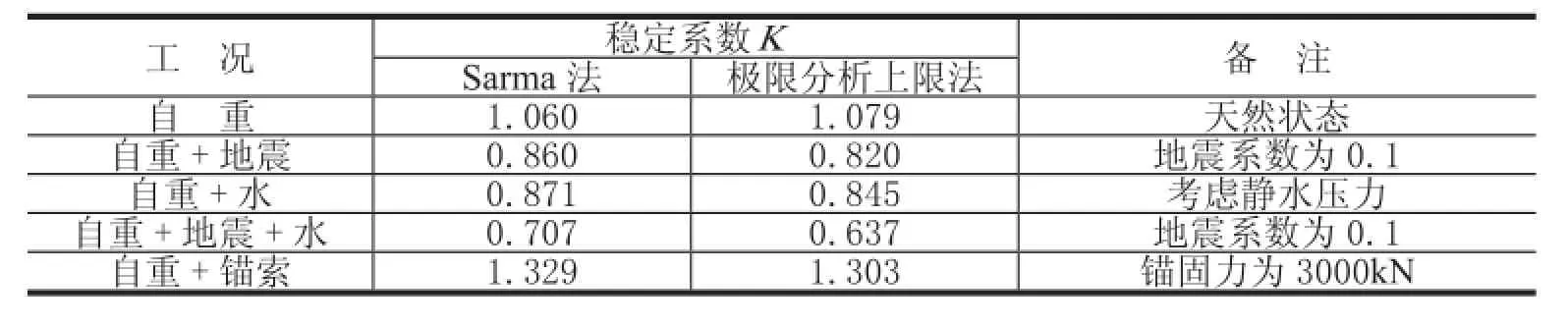
表9-4 两种方法稳定系数计算结果对比

尽管算例在天然状态处于基本稳定状态，但在考虑地震作用力和裂隙水压力的情况下，都会产生滑动破坏，因此属于潜在不稳定岩质边坡，需要采用加固方案提高整体稳定性（图9-3）。通过给边坡第三个滑体单元滑面分别施加1 000kN级、2 000kN级、3 000kN级、4 000kN级、5 000kN级和6 000kN级的预应力锚索锚固工程，选用锚固力、地震作用力（水平地震系数Kc=0.1）和裂隙水压力三个影响稳定系数的因素组合（不同工况），采用极限分析上限法分别进行了稳定性分析计算，结果见表9-5。计算结果显示，当锚固力达到6 000kN时，单独考虑水和地震条件下的稳定系数Fs都大于1.1，但在最不利组合情况下，边坡稳定系数依然小于1.0。总的来讲，随着锚固力的增加，边坡稳定系数在各种工况条件下均有所提高。

表9-5 不同锚固力作用下的稳定系数计算结果

地震作用是影响边坡稳定性的一个重要因素，所以有必要分析加锚岩质边坡上限法稳定系数计算结果与地震系数的关系。当地震烈度为Ⅶ度、Ⅷ度和Ⅸ度，对应水平地震系数Kc分别取0.1，0.2和0.4时，采用文中方法计算了锚固力为3 000kN和6 000kN的稳定系数，并绘制了关系曲线（见图9-4）。曲线直观地给出了地震作用和锚固之间的关系，可以得到三点结论：① 相同锚固力条件下的边坡稳定系数随地震烈度的增强而减小；② 相同地震烈度条件下的边坡稳定系数随锚固力增加而提高；③ 稳定系数与水平地震系数呈非线性变化，当地震系数较小时，稳定系数下降速度较快，而当地震系数变大时，稳定系数下降速度较平缓。

图9-4 不同锚固力的水平地震系数和稳定系数对比关系曲线

最后，对于稳定系数的计算方法提出一点新的看法。由于稳定系数K是隐式出现的，所以通常采用迭代的计算方法来求解，但通过实际的应用，笔者发现常规的迭代方法收敛性较差，计算效果不佳。建议采用“等K法”来实现稳定系数计算，其具体的步骤是：① 给定稳定系数K的求解范围，并设置稳定系数初始值；② 设定循环语句步长（10-6）；③ 通过式（9-19）得到稳定系数计算值；④ 执行循环语句，得到一系列稳定系数初始值和计算值；⑤ 绘制初始值、计算值和对应循环次数的关系曲线，其交点即为稳定系数的最终解。

图9-5显示的是该边坡在自重条件下，采用等K法绘制的曲线，其交点显示稳定系数计算值为K=1.079。

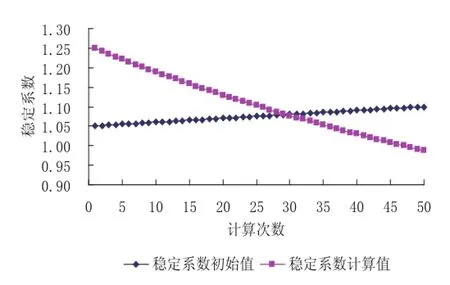
图9-5 稳定系数最终计算结果确定方法