6 边坡加固方法研究

6 边坡加固方法研究

6.1 土钉支护结构的极限分析上限法

图6-1 土钉支护结构极限分析示意图

设土钉支护采取等倾角、等间距支护方式，土钉倾角为α，水平间距和垂直间距分别为Sh和Sv。设第i层土钉钉头距地面距离为Si，与坡面交点为D，与对数螺旋线滑裂面（潜在的）交点为Ei，如图6-1所示。Ei点在直角坐标系的坐标为（xEi，yEi），在极坐标系中对应的极角为θEi；D点在直角坐标系的坐标为（xD，yD），在极坐标系中对应的极角为θD。由图6-1中的几何关系（秦四清，等，1999），可得

由式（6-4）可得

因为Ei点在对数螺旋线上，因此Ei点的坐标也满足如下的关系：

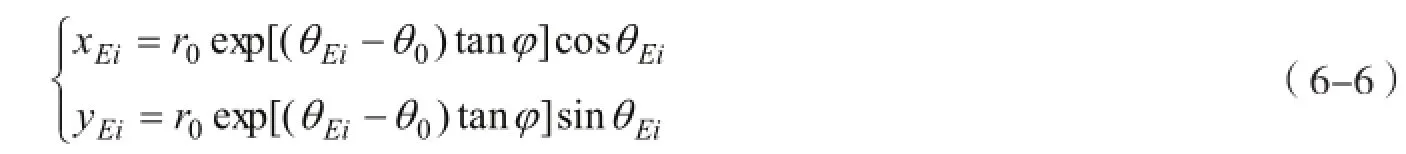
将式（6-6）代入式（6-5）中，整理后得

Ei点处的塑性应变速度vEi为

第i层土钉的外力功率为

式中：θEi为第i层土钉与对数螺旋线交点Ei的极角，Sh为土钉水平间距，pRi为第i层土钉抗拔力。设第i层土钉总长度为li，DE长度为lai（滑动体内部的长度），则第i层土钉在稳定区内的长度为lbi=li-lai。因为，应变速度vEi（Ei点处）沿土钉分量的矢量方向与抗拔力pRi的方向相反，因此，土钉抗拔力沿应变速度场做负功。所有土钉外力功率和为

令

则有

根据极限分析上限定理，将式（6-10）～式（6-14）代入到虚功率方程中，得

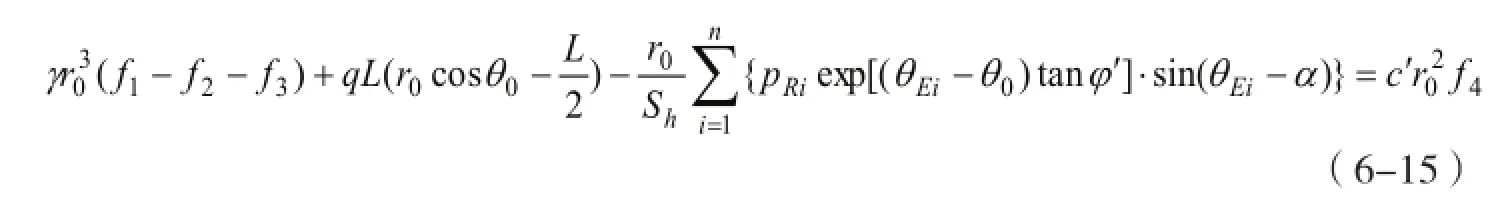
整理为

式（6-16）即为土钉支护结构的极限分析上限法虚功率方程，可以通过Powell 所建议的数学规划方法（Powell，1964）确定参数θ0/θh的临界值，所对应的强度折减系数即为土钉支护后最危险滑裂面的稳定系数或安全系数（梁仕华，等，2005；Juran，等，1990；John，1990）。

6.2 抗滑桩加固土坡的极限分析上限法

图6-2 抗滑桩加固边坡稳定性问题

当采用抗滑桩增加边坡稳定性时，如图6-2所示，可以假定一个侧向力F和力矩M作用于潜在对数螺旋线滑面以上的抗滑桩上。在这种假定条件下，抗滑桩作用于滑体的外力功率计算公式为

式中：tanφ'=tanφ/K，K为边坡的设计安全系数；θF为抗滑桩与滑裂面的交点所确定的位置（极角），F为抗滑桩提供的单位宽度土体阻滑力；M为滑裂面以上阻滑力F产生的力矩，其计算公式为

式中：h是滑裂面以上抗滑桩的长度；m是抗滑桩侧向有效阻滑力合力作用点和桩顶之间的距离与滑裂面以上的抗滑桩长度h之比，是一个经验系数，一般小于1。M的取值取决于桩侧阻滑力的分布模式，对于抗力线性分布情况，m=1/3；对于均匀分布情况，m=1/2；若m=0，则相当于仅考虑抗滑桩与滑裂面的剪力效应。滑裂面以上的抗滑桩长度h可以用以下的公式表达（Αusilio，等，2001；年廷凯，等，2004，2005）：

式中：

令

则有

根据极限分析上限定理，将式（6-17）代入到虚功率方程中，得

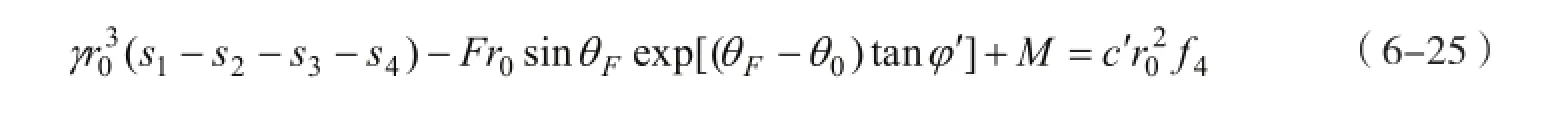
进一步可以整理为阻滑力F的函数关系：

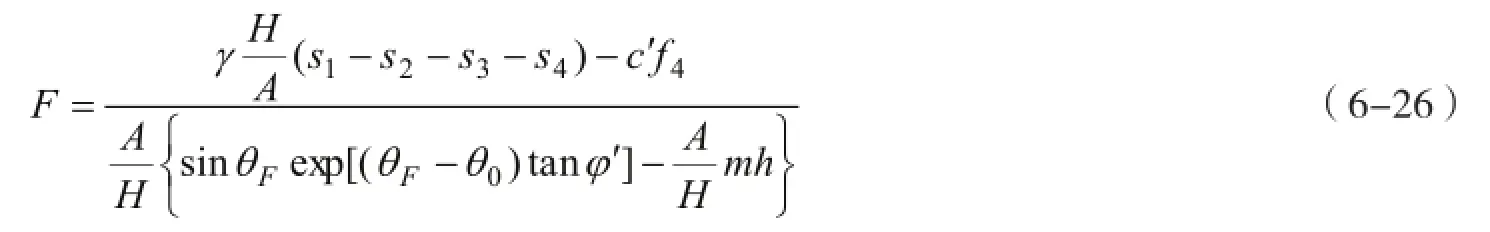
式（6-26）即为设计安全系数条件下，单排抗滑桩所需要提供的单位宽度土体的阻滑力。多排抗滑桩的情况，阻滑力可以通过叠加的原理求解。为了获得作用于抗滑桩适合的阻滑力，相邻抗滑桩的“土拱效应”应被考虑。

当土坡布置抗滑桩后，稳定系数和潜在破坏机构都会发生相应的变化，因此，会出现更多的临界滑动面的情况。最危险的滑动面位置，对应给定设计安全系数条件下，抗滑桩发挥阻滑作用最大情况，即F值最大。从计算的角度出发，最危险滑动面的位置可以通过函数F=F(θ0, θh, θF, β')的极值条件得到。当然，前提条件是抗滑桩的位置要预先给定。极值条件及临界状态条件的方程为

式中：xF表示抗滑桩的位置，为抗滑桩与坡脚的水平距离。式（6-27）中未知量包括θ0，θh，β' 和θF。角θ0，θh和β' 指出了潜在极限状态滑裂面的位置，将这三个量值代入到式（6-26）中，可以计算得到阻滑力F的最大值。

对第4章第4.4小节典型算例进行加抗滑桩后的稳定性分析计算。当没有抗滑桩时，稳定系数K=1.11，需要布置抗滑桩提高边坡的整体稳定性。考虑在xF=13.7m处设置抗滑桩，加固后设计安全系数K=1.50。假定桩侧阻滑力按照三角形分布，即取m=1/3，则按照上述方法所确定的桩侧极限有效滑坡推力为517.5 kN·m-1。通过公式（6-19）计算得到滑裂面以上抗滑桩长度为12.7m，因此，抗滑桩的全长可以取为Lp≈2h=25m。如图6-3所示，采用抗滑桩加固边坡后，潜在滑裂面深度增大，并且剪出口超出坡脚一定的范围。

图6-3 无抗滑桩和有抗滑桩两种情况下的土坡极限滑裂面（Ausilio，等，2001）

6.3 加筋土坡的极限分析上限法

图6-4 加筋土质边坡刚体旋转破坏机制

对于加筋土质边坡（见图6-4），土工格栅所产生的外力功率计算是重点。假定土工格栅在加筋土工结构中只承受拉力，并且土工格栅具有足够的长度，那么筋材只能产生拉伸变形与拉破裂。如图6-5所示，速度间断面单位面积上筋材的能量耗散率为（王钊，等，2005；乔丽平，等，2006；肖成志，等，2005；崔新壮，等，2007）

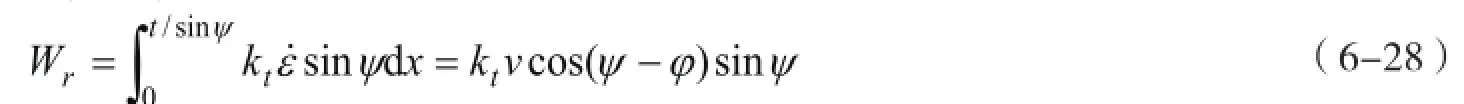
式中：T为筋材拉伸强度（kN·m-1）；s为筋材层间距（m）；n为加筋层数。

图6-5 速度不连续面上的筋材破坏

筋材沿着整个对数螺旋线滑裂面的外力功率可以通过单位面积上的能量耗散率公式（6-28）积分计算得到：

筋材拉力沿应变速度场做负功，所以总的筋材能量耗散率为负值。考虑到dl=rdθ/cosφ，ψ=π/2-θ+φ，式（6-30）经积分求和得到：

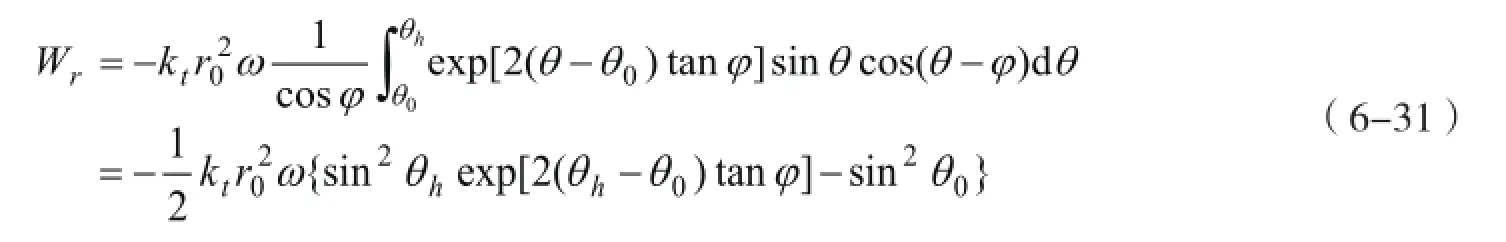
式（6-31）代入到虚功率方程中，消除掉角速度项，得

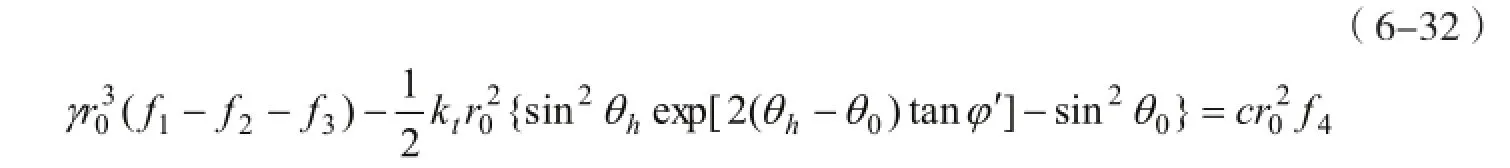
整理后，得到加筋土坡的临界高度计算公式为

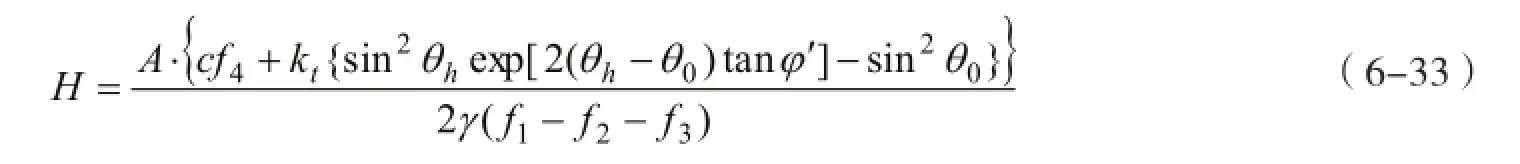
式中：φ'=arctan(tanφ/K)，Α=sinθhexp[(θh-θ0)tanφ']-sinθ0。特别注意，Α，f1，f2，f3和f4的表达式中隐含有φ'。

假定加筋土坡处于极限平衡状态即K=1时，由式（6-33）可确定土坡的临界自稳高度Hmin=Hcr。当给定坡高时，强度折减系数K是两个待定变量θ0、θh的非线性隐式函数，可以利用式（6-33）的极值条件确定强度折减系数的临界值（整体稳定系数）及其相应的临界破坏机构。极值条件及临界状态条件的方程为：

采用迭代的方法，逐步折减土的强度参数（c与φ）直至获得的极限坡高等于加筋土坡的实际高度，则此时的强度折减系数K为加筋边坡的稳定系数解，与之相应的参数θ0、θh确定加筋土坡的临界失稳机构。

文献（Porbaha，等，1996，2000）给出了加筋土坡临界高度极限分析上限解和模型试验的对比结果。已知填土容重γ=17.85 kN·m-3，有关参数和结果见表6-1。对比分析显示，由式（6-33）计算得到的临界高度要比试验实测值小约10%～15%，可能有如下几个方面原因：① 理论计算中只考虑了筋材的拉力破坏，而筋材拉力破坏的发生到模型土坡的完全破坏还有一个渐进的过程，理论计算中忽略了这一渐进过程的能量损耗；② 计算中T采用的由筋材的宽条试验得到的拉伸强度，其作用并未完全发挥出来，有关T的取值，有待进一步研究；③ 离心试验中，箱壁不可能绝对光滑，箱壁与模型间的摩擦力使得试验结果本身就有一定误差。

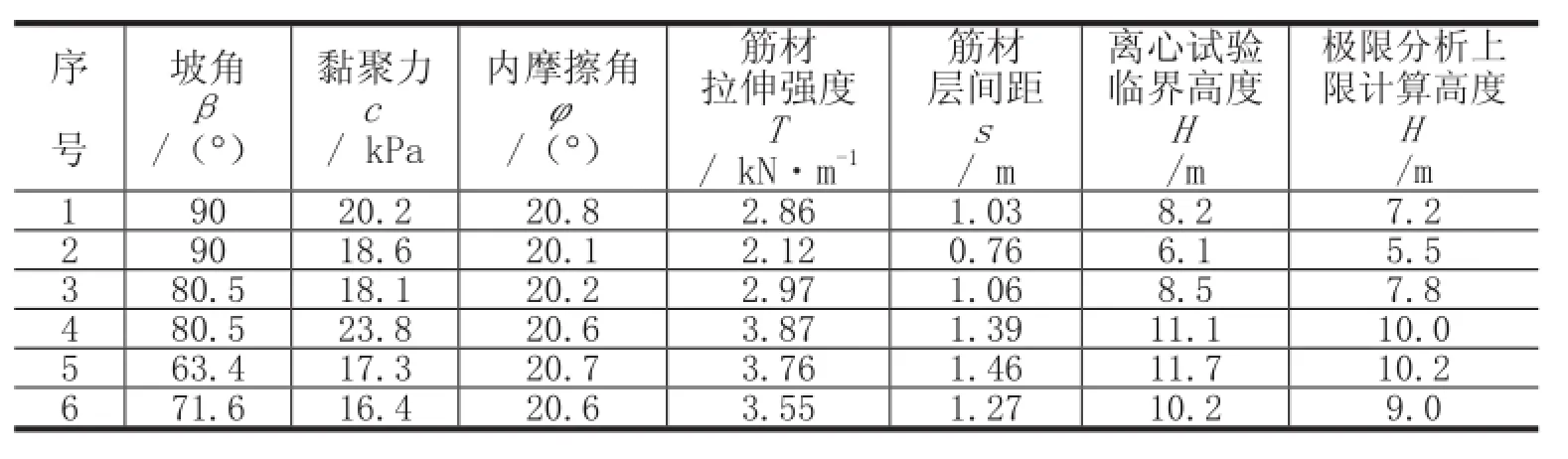
表6-1 加筋土坡临界高度理论计算与试验对比（Porbaha，等，2000）

6.4 挡土墙主动土压力的极限分析上限法

经典的库仑与朗肯土压力理论概念明确、计算简单，一直在工程中得到广泛的应用。但是朗肯土压力理论要求挡土墙墙背直立、光滑、墙后填土水平并延伸至无穷远，且不考虑墙背与填土之间的摩擦作用。而库仑土压力理论假设墙背填土为无黏性土，要求滑裂面为平面。这些假设和要求都限制了其应用范围，并影响了其计算结果的准确性（尹宏磊，等，2006）。

基于塑性力学上限定理的极限分析方法，在主动土压力计算方面也具有一定的代表性。这种方法具有坚实的理论基础，利用经典塑性力学的上限定理从上限方向逼近真实解。在许多简单的问题中，其计算结果都与工程中广泛采用的极限平衡法得到的结果相同（陈惠发，1975；Yang，2007）。

传统的主动土压力计算，假定滑裂面为平面或组合滑面，但多数挡土墙支护的土质边坡破坏实例显示，破坏面多为近光滑曲面。因此，本节在推导主动土压力的极限分析上限解公式时，仍选择滑裂面为对数螺旋线。

作用在滑动土体上的外力有滑动土体的重力W和挡土墙对滑动土体的反力——主动土压力Pa。主动土压力Pa的作用线与挡土墙墙面的法线成δ角，作用方向指向填土，作用点在墙背高度的2/3处（C点）。主动土压力Pa可分解为两部分，即水平分量Pacos(α+δ)和铅直分量Pasin(α+δ)。如图6-6所示，B点坐标为（rhcosθh，rhsinθh），Α点坐标为（r0cosθ0-L，r0sinθ0），因此，C点坐标为

图6-6 主动土压力计算的极限分析上限法

挡土墙主动土压力Pa的水平分量Pacos(α+δ)与应变速率v的水平分量方向相反，因此这部分外力功率为负值，计算公式为

挡土墙主动土压力Pa的铅直分量Pasin(α+δ)与应变速率v的铅直分量方向相反，因此这部分外力功率也为负值，计算公式为

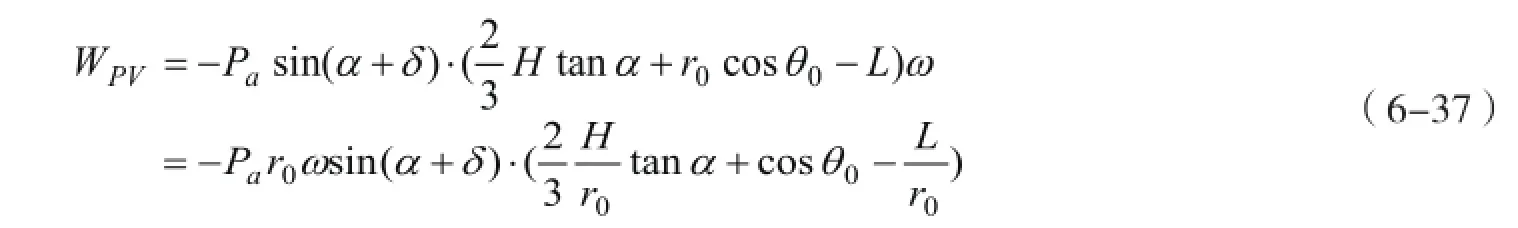
挡土墙主动土压力Pa产生的总外力功率为

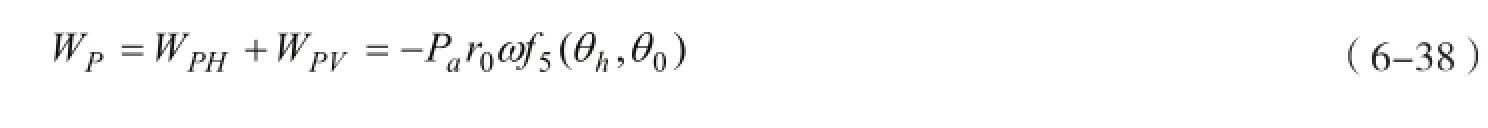
式中：

以下将f5(θh,θ0)简记为f5。根据极限分析上限定理，将式（6-38）代入到虚功率方程中，消除掉角速度ω项得

整理后，得到主动土压力计算公式为：

式中：A，f1，f2，f3，f4和f5中隐含φ'=arctan(tanφ/K)的条件。当fs取值为1.0时，可以通过式（6-41）计算得到主动土压力的值。最危险的滑动面位置，对应给定设计安全系数K条件下，挡土墙发挥抗滑作用最大的情况，即Pa值最大。对应主动土压力Pa即为设计挡土墙应该提供的反力。极值条件方程为

某挡土墙墙高H=10m，墙面水平，填土为黏性土，γ=18 kN·m-3，φ=30°，c=10 kPa，填土表面水平（喻则红，等，2006）。测得实际所受主动土压力Pa值为188.08kN；用经典的朗肯主动土压力公式进行计算，得到的主动土压力Pa值为195.7kN；如果用极限分析上限法得到的公式（6-41）计算，则得到Pa值为189.4kN。对比分析可以发现，利用极限分析上限法推导出的计算挡土墙主动土压力公式，其计算结果比朗肯法稍小，但与实测值更为接近。