4 岩质崩塌稳定评价计算方法

4 岩质崩塌稳定评价计算方法

4.1 倾倒式崩塌稳定性计算

作用在倾倒式崩塌岩体上的作用力主要有自重荷载、后缘裂隙水压力及地震惯性力等，自重为危岩体的体积与天然容重的乘积；裂隙水压力与切割危岩体结构面张开程度密切相关，主要考虑静水压力，天然状态取三分之一孔隙水柱高，暴雨期间取三分之二孔隙水柱高；地震力因素方面，到目前为止，主要考虑水平地震荷载的作用，为危岩体自重与水平地震系数的乘积，对于长期累积地震荷载变形以及振动对危岩体稳定性的影响尚无成熟方法计算。倾倒式崩塌稳定性计算采用极限平衡理论，按如下几种工况分别进行：

组合1：自重+裂隙水压力（天然状态）

组合2：自重+裂隙水压力（暴雨状态）

组合3：自重+裂隙水压力（天然状态）+地震力

岩体被结构面从坡体切割成长高板状或柱状块体，呈近直立状。块体底部由结构面（或岩层界面）与坡体相连。此时块体失稳方式有两种：①在水平力作用下岩体发生倾倒；②因差异风化使底部岩体风化剥落严重，产生岩腔，不能支撑上部岩体重量发生倾倒。

4.1.1 水平力作用下岩体发生倾倒式崩塌

在水平作用力下岩体发生倾倒式崩塌的基本受力情况如图4-1所示，一旦发生倾斜，将以Α点为转动支点发生转动。

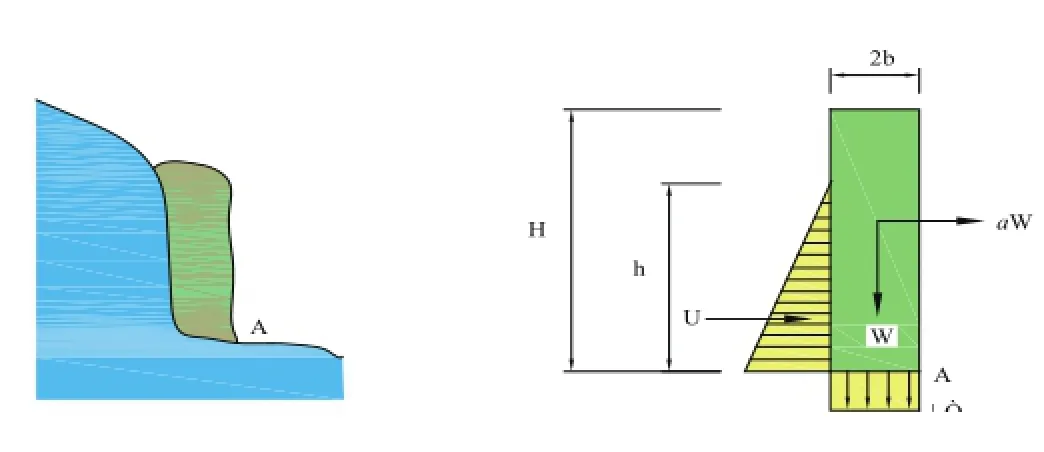
图4-1 倾倒型崩塌计算图

同时考虑裂隙水压力U、重力W、地震力aW、岩体底部抗拉力强度σt等因素，根据力学分析，崩塌体的抗倾覆稳定性系数K按下式计算：

当地震烈度为Ⅶ度时，取a=0.1，当地震烈度为Ⅷ度时，取a=0.2，当地震烈度为Ⅸ度时，取a=0.4。

4.1.2 底部有岩腔时岩体发生倾倒式崩塌

因差异风化使底部岩体风化剥落严重，产生岩腔，不能支撑上部岩体重量发生倾倒式崩塌的基本受力情况如图4-2、图4-3所示，图中C点为危岩体底部与基座接触的可能倾覆点。

图4-2 重心在转动支点内侧计算模型

图4-3 重心在转动支点外侧计算模型

（1）危岩体重心在倾覆点内侧时，倾倒型崩塌计算模型见图4-2，按单位长度考虑，围绕可能倾覆点C，倾覆力矩为：

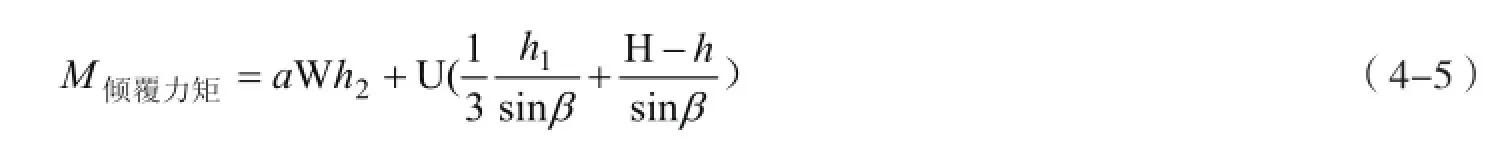
抗倾覆力矩为

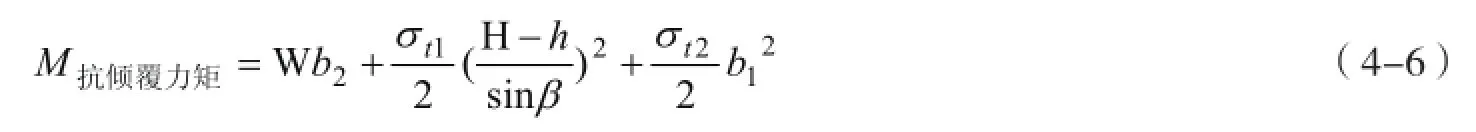
稳定系数为

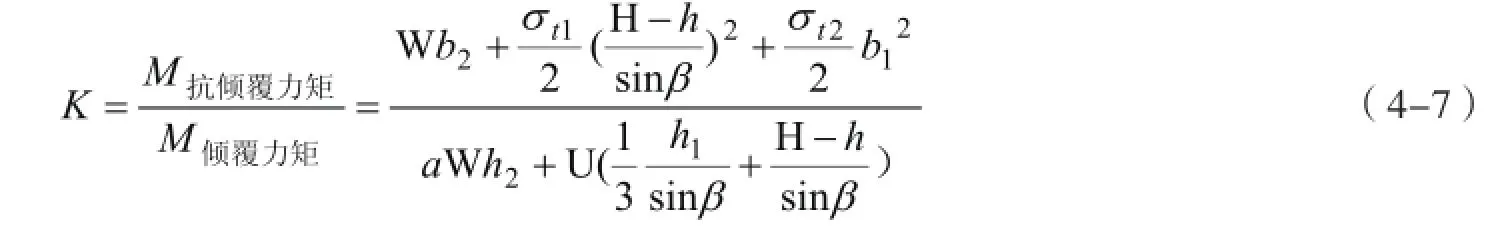
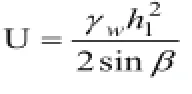
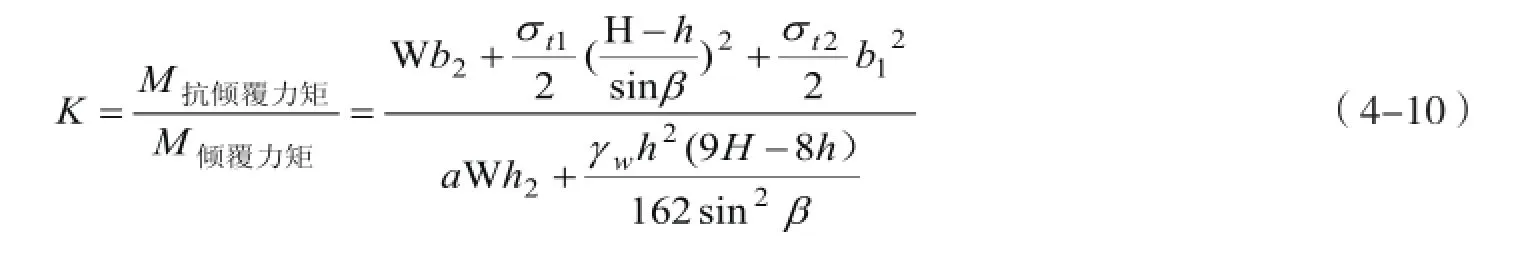
（2）危岩体重心在倾覆点外侧时，倾倒型崩塌计算模型见图4-3，按单位长度考虑，围绕可能倾覆点C，倾覆力矩为

抗倾覆力矩为

稳定系数为

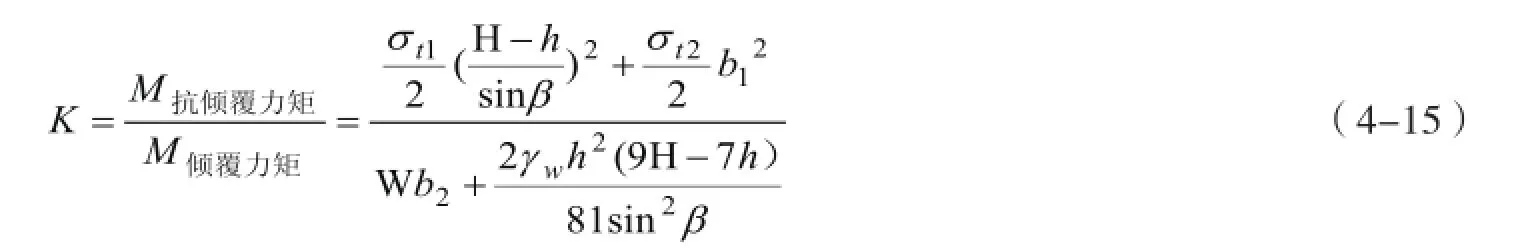
4.2 拉裂式崩塌稳定性计算

4.2.1 悬臂-拉裂式崩塌计算

1）最大弯矩截面处无拉裂缝情况

悬臂-拉裂式崩塌如图4-4所示。当下部软岩和上部软岩不断风化剥落，中间的硬岩就以悬臂梁形式凸出。根据悬臂梁受力分析，在ΑB面上承受最大的弯矩和剪力，岩体顶部受拉，底部受压，Α点拉应力最大。在长期重力作用和风化作用下，Α点附近的裂隙逐渐扩大，并向深部发展。一旦Α点处拉应力超过岩石的抗拉强度，悬臂状岩体就会发生崩塌。因此，这类崩塌的关键是最大弯矩截面ΑB上的拉应力能否超过岩石的抗拉强度σt。故可以用拉应力与岩石抗拉强度的比值（最大拉应力-抗拉强度比值分析法）进行稳定性检验。假设凸出的悬臂梁岩体长度为b，岩体厚度为l，宽度为1m（取单位宽度），岩体重度为γ。当ΑB断面上未出现裂缝时，则Α点上的拉应力为（王根龙，等，2012）：

最大弯矩截面处无拉裂缝情况下，最大拉应力-抗拉强度比值分析法推导得到的稳定系数为

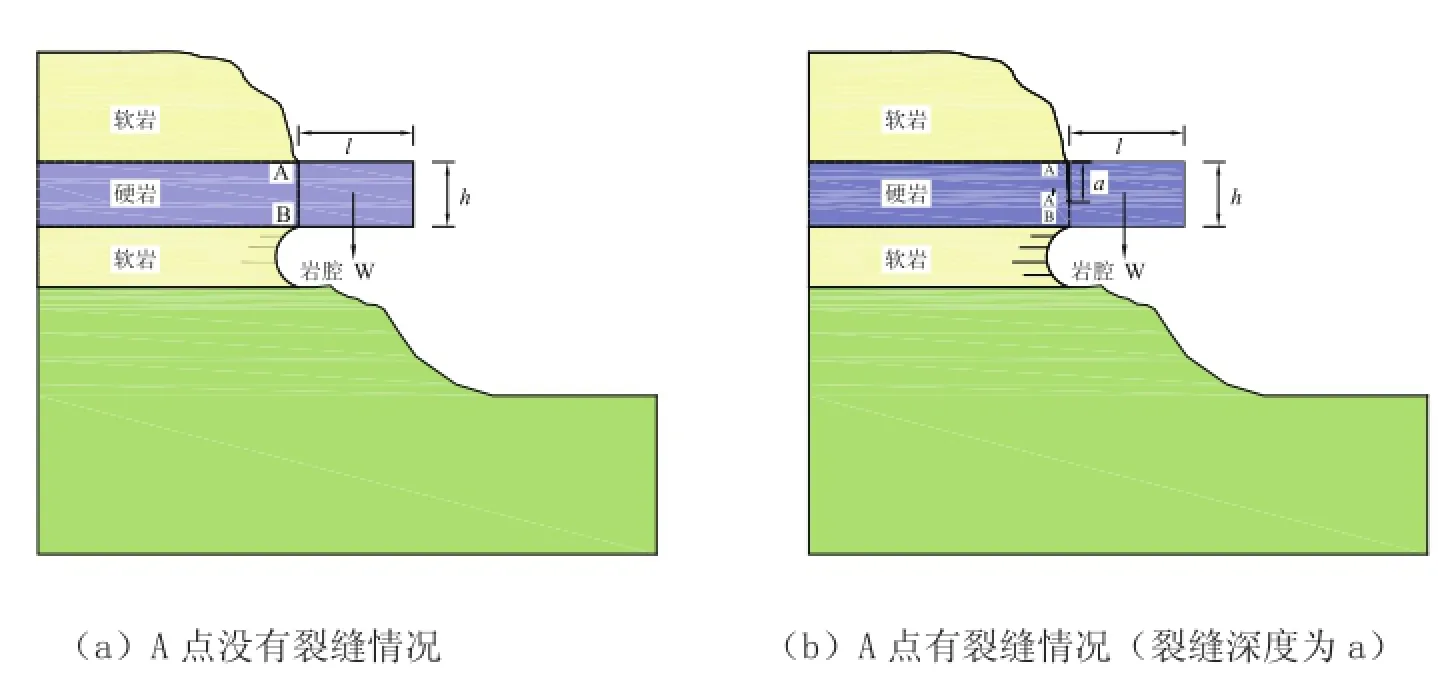
图4-4 悬臂-拉裂式崩塌计算模型

2）最大弯矩截面处有拉裂缝情况

最大弯矩截面处有拉裂缝情况下，最大拉应力-抗拉强度比值分析法推导得到的稳定系数为

4.2.2 塑流-拉裂式崩塌计算

当陡峻边坡岩体下部有较厚的软弱层时（常为断层破碎带、风化破碎岩土体等），在水的作用下，这些软弱层先进行软化，随后发生塑流-拉裂式崩塌。以下介绍抗压强度-压应力比值分析、软弱层挤出变形分析两种计算方法（王根龙，等，2013）。

1）抗压强度-压应力比值分析计算

当上部岩体在软弱层产生的压应力大于软弱层的无侧限抗压强度时，则软弱层将被挤出，即发生鼓胀变形。上部岩体可能产生下沉、滑移或倾斜，甚至发生崩塌。如图4-5所示。稳定性系数可用下部软弱层的无侧限抗压强度与上部岩体在软岩顶面产生的压应力的比值计算：

式中：W为上部潜在崩塌体的重量（kPa）；Α为潜在崩塌体的底面积；σc为下部软弱层天然状态下的无侧限抗压强度（kPa）。

图4-5 软弱层压缩挤出变形引致崩塌灾害示意图

2）软弱层挤出变形分析计算

在地下水的作用下，下部软弱岩层或者厚度较大的软弱夹层先行软化，随后，在上部岩体压力作用下，软弱岩层或夹层物质产生不均匀变形，从而导致软弱基座式岩体以压缩变形-倾倒（剪切）模式发生崩塌如图4-6所示。

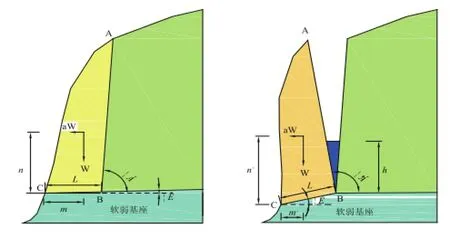
图4-6 软弱基座塑流-拉裂式崩塌计算模型

软弱岩层或软弱夹层被挤出，危岩体不均匀沉降，C点沉降大于B点，沉降的实际值较难确定。假设B点沉降量为零，C点因挤压产生沉降变形位置如图4-6所示，此时，潜在崩塌体可能的失稳方式是以C点为支点倾倒，也可能以BC面为滑面滑移，需要计算两种失稳方式的稳定性。

当以C点为支点倾倒时，稳定性系数K为

当沿着BC滑动面滑移时，稳定系数K为

式中：W为潜在崩塌体的重量(kN·m-1)；aW为地震力，a代表地震影响系数，大小为水平地震动峰值加速度与重力加速度g的比值（无量纲），对地震烈度为Ⅶ度、Ⅷ度和Ⅸ度地区，水平地震影响系数a应分别取0.1、0.2和0.4；U1为后缘结构面ΑB静水压力（kN）；U2为底部结构面BC静水压力（kN）。U1和U2的表达式分别为

式中：m，m'分别为不均匀压缩前后C点到重力作用线的距离（m）；n，n'分别为不均匀压缩前后C点到水平地震力作用线的距离（m）；θ，θ'分别为不均匀压缩前后底部结构面BC的倾角（°）；α，α'分别为不均匀压缩前后后缘结构面ΑB的倾角（°）；h为后缘充水高度（m）；L为底部滑面的长度（m），γw为水的重度；c为结构面BC的内聚力；φ为结构面BC的内摩擦角。

4.2.3 拉裂-坠落式崩塌计算

1）刚体极限平衡法

拉裂-坠落式崩塌是指危岩体裂缝（主控结构面）已经产生，但并未完全贯通，通过计算主控结构面的抗剪强度和平均剪应力，将其比值定义为拉裂-坠落式崩塌的稳定系数。计算模型见图4-7，重力和地震力沿着主控结构面的法向分量和切向分量可沿主控结构面进行分解，分别由式（4-26）和式（4-27）计算，进而可得主控结构面上的平均法向应力和平均剪切应力，分别由式（4-28）和式（4-29）计算。

图4-7 拉裂坠落式崩塌计算模型

法向分量

切向分量

主控结构面抗剪强度由τf= c+σtanφ式计算。对于荷载组合1，危岩稳定性系数为

对于荷载组合3，危岩稳定系数为

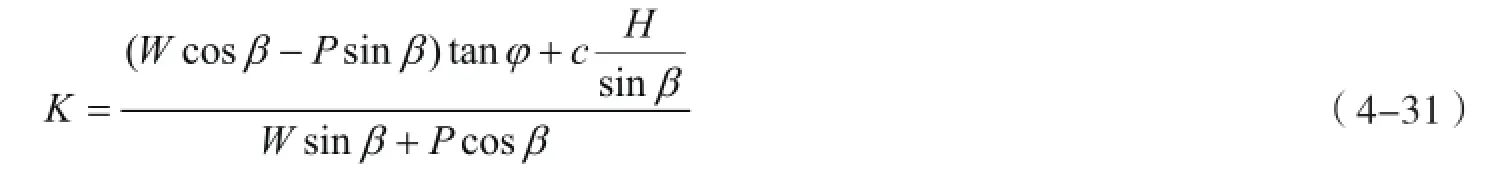
2）断裂力学分析法

对于危岩主控结构面（见图4-8），尖端任意点Q的断裂角为θ0，则沿着θ0方向的危岩联合断裂强度因子Ke的计算方法表述如下：

图4-8 危岩断裂力学模式

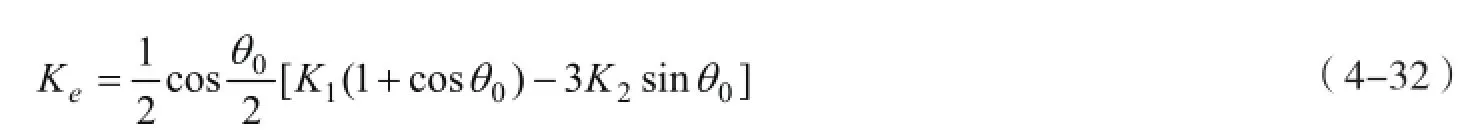
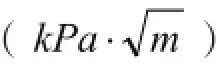
为了求解θ0，令主控结构面尖端τrθ= 0，即：

当K2≠0时，令k=(K1K/2)2，则推导可得

进而有

根据K1和K2，并将式(4-35)代入式(4-32)可求得联合断裂强度因子Ke。于是，基于主控结构面联合断裂强度因子和危岩完整岩石得断裂韧度便可建立危岩稳定系数的断裂力学表达式。

式中：Ke需要通过不同类型危岩在不同荷载组合下进行求解；断裂韧度KIC则需要对组成危岩体的完整岩石进行断裂力学实验确定。

该计算方法普遍适合于每类危岩，重点关注危岩主控结构面的失稳断裂问题。

4.3 剪切-滑移式崩塌稳定性计算

4.3.1 刚体极限平衡法

1）稳定计算基本假定及分析步骤

滑移式崩塌稳定性分析目前用的最多的是块体极限平衡法，块体极限平衡法的假设条件：① 边坡岩体将沿某一结构面（滑动面）产生滑移剪切破坏；②滑体在滑动过程中相对位置不变化，即为刚体；③ 滑动面上的应力分布均匀；④ 不考虑滑体两侧的抗滑力。

在上述假设的基础上，按下式计算稳定性系数：

（1）若K＞1，稳定

（2）若K≤1，不稳定

在多数情况下，计算的稳定性系数都有一定误差，因此，为保险起见，引入安全系数的概念。

块体极限平衡法步骤：① 可能滑动岩体几何边界条件；② 受力条件；③ 确定计算参数；④ 计算稳定性系数；⑤ 确定安全系数，进行稳定性评价。

几何边界条件是指构成可能滑动岩体的各种边界面及其组合关系，包括滑动面、切割面和临空面三种。滑动面是指起滑动(失稳岩体沿其滑动)作用的面，包括潜在破坏面。切割面是指起切割岩体作用的面，由于失稳岩体不沿该面滑动，因而不起抗滑作用，如平面滑动的侧向切割面。临空面指临空的自由面，它的存在为滑动岩体提供活动空间，临空面常由地面或开挖面组成。

几何边界条件分析的内容是查清岩体中的各类结构面及其组合关系，确定出可能的滑移面、切割面。几何边界条件分析的目的是确定边坡中可能滑动岩体的位置、规模及形态，定性地判断边坡岩体的破坏类型及主滑方向。几何边界条件的分析可通过赤平投影、实体比例投影等图解法或三角几何分析法进行。

在工程使用期间，可能滑动岩体或其边界面上承受的力的类型及大小、方向和合力的作用点统称为受力条件。边坡岩体上承受的力常见有：岩体重力、静水压力、动水压力、建筑物作用力及地震力等。

2）刚体极限平衡法分析计算

剪切-滑移式崩塌可有以下4种型式（见图4-9），其中前3种形式分别为：① 下伏岩体在上部岩体巨大自重作用下，沿着边坡中软弱结构面剪裂；② 岩层比较软弱，破碎的开挖边坡在重力作用下发生剪切滑落；③ 危岩体沿着结构面发生剪切滑动，导致崩塌。

根据图4-10，剪切面上法向力和切向力分别为

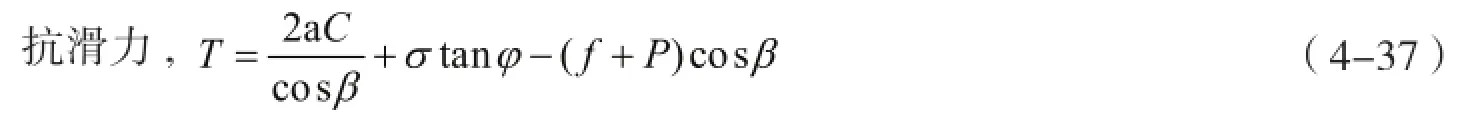
式中：

稳定性系数

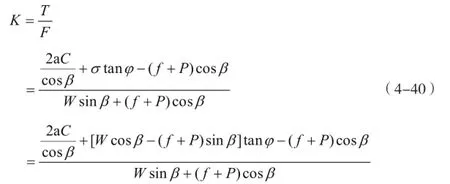
式中：C为软弱结构面内聚力；φ为软弱结构面内摩擦角；β为危岩体滑面倾角。

图4-9 滑移式崩塌类型

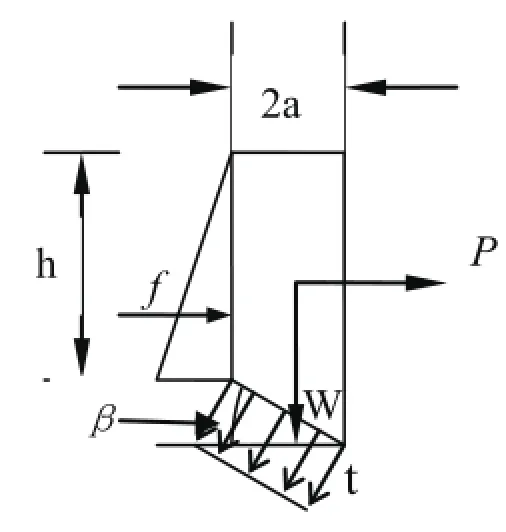
图4-10 剪切式崩塌计算图

对于剪切型崩塌的第四种情况，有两种可能，如图4-11所示，讨论如下：

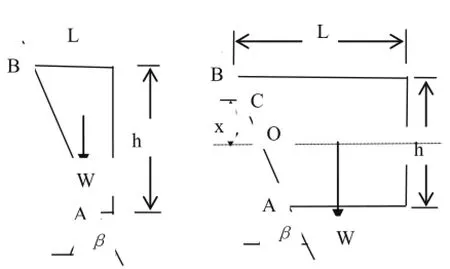
图4-11 剪切式崩塌向拉张式崩塌转化计算图

设边坡表面危岩体重力为G，水平长度为L（忽略因边坡角度变化而对下底长度和G的影响），高为h，边坡结构面角度为β，上边界与边坡交点为B，下边界与边坡交点为Α。当重力作用线与坡面交点在Α点内侧或重合时，危岩体的失稳方式只能是沿着结构面BΑ克服抗剪阻力向下滑动，此时稳定性计算可用公式（4-40）计算。当重力作用线与坡面交点在Α点外侧时，根据材料力学可知，危岩体将在重力作用下，在结构面BΑ面上产生拉力，拉力最大位置在B点处。此时，危岩体的失稳方式除了可能沿着BΑ面剪切破坏外，还可能因拉应力超过结构面上抗拉强度而产生拉张破坏。BΑ面上的拉应力计算如下：

设危岩体中心轴与边坡交点为O点，BΑ面上任一点C距O点距离为x，当β＜90°时，C点处拉应力（苏天明，等，2006）为

保证危岩体稳定的判据为：σB≥ σt，σt为岩体结构面BΑ面抗拉强度。

设L=3m，h=2m，γ=2500kN/m3时，画出B点处拉应力随β的增大而变化关系示意图。

β角理论上可以是从0°～180°之间的任一角度，因此，B点的拉应力为一周期为π的正弦函数，最大值是在β=135°时，即此时悬臂岩体最容易产生拉张破坏；当β=45°时，B点拉应力最小，如图4-12所示。

当坡角β和块体高度h保持不变时，B点拉应力随着L的增大而增大，与L呈正比关系；

当坡角β和块体长度L保持不变时，B点拉应力随着h的增大而减小，呈负指数函数。

图4-12 B点处拉应力-坡角关系曲线图

4.3.2 极限分析上限法（能量法）

1）基本原理

极限分析上限法是同刚体极限平衡法根本不同的一种方法，是将物体的本构关系简化为理想刚塑性应力-应变关系，利用刚塑性体处于极限状态的普遍原理——上下限定理中的上限定理求解极限荷载的一种分析方法。极限分析中的上限定理得到的是精确解答的上限。它的理论基础是塑性力学的塑性位势理论，它的最大优点在于物理概念清楚，计算也较简单。

岩质边坡极限分析上限法的要旨是：当滑动体滑动时，外力所做的功率等于内力（滑面上的阻力）所消耗的功率。于是，可由滑体处于极限状态时两功率相等的条件，得到虚功率方程（王根龙，等，2009）。

式中：等号左端为滑面上阻力产生的内部耗散能，等号右端为外力所做的功率；Г为岩质边坡滑面；D为作用在滑面的内能耗散；T*为极限状态外荷载；v为滑面处的应变速度。

由于篇幅所限，有关极限分析上限法的基本原理这里就不再赘述，这里仅对平面滑动型岩质边坡极限分析上限法的公式进行推导。

2）岩质边坡极限分析上限解

（1）外力功率

如图4-13、图4-14所示，作用在岩质边坡上的外力包括后缘裂缝静水压力、沿滑面扬压力、重力、地震惯性力、预应力锚索（杆）锚固力，计算公式分别为

图4-13 平面滑动型岩质边坡稳定性分析计算模型

图4-14 极限分析上限法破坏机构——速度场

① 后缘裂缝静水压力PW

② 沿滑面扬压力U

③ 水平地震惯性力E

式中：a为水平地震影响系数，大小为水平地震动峰值加速度与重力加速度g的比值（无量纲），对地震烈度为Ⅶ度、Ⅷ度和Ⅸ度地区，水平地震影响系数a应分别取0.1、0.2和0.4；W为滑体重量(kN·m-1)。

④ 预应力锚索（杆）锚固力Rm

式中：Rmi为第i道预应力锚索（杆）在每延米范围内提供的锚固力（kN·m-1）。

为了求得滑体上外荷载所做的功率，同时便于进行公式推导，这里将滑体自重荷载W、沿滑面扬压力U、后缘张裂缝静水压力PW、水平地震惯性力E、预应力锚索（杆）锚固力Rm共5个外力，分解后合成为水平力分量Fx和铅直力分量Fy，其计算公式分别为：

这些外力在应变速度场v上所做的总功率计算公式为

（2）内部耗散能。

滑面上的力有剪切力和法向力，其中剪切力包括两部分，一部分为黏聚力C，它是已知的，其值为cL；另一部分是摩擦力，其值为Ntanφ，它和法向力N一起，构成一个与滑面法线方向夹角为φ的合力P（见图4-14）——“组合摩擦力”。这个组合摩擦力的大小通常是未知的，但它的方向是已知的，即与法线方向夹角为φ。如前所述，塑性速度v与滑面夹角为φ，这样“组合摩擦力”P与塑性速度v正交，所以P在v上所做的功为零。

通过分析可知，在计算滑面上阻力产生的内部耗散能时，只有黏聚力C在应变速度场v上做功，其计算公式为

（3）极限分析上限解，

对于岩质边坡，按照极限分析理论构建虚功率方程（4-43）时，应该满足极限破坏状态的前提条件。要使岩质边坡沿滑面过渡到极限破坏状态，可以采用强度折减法，即对边坡滑面的强度参数c和tanφ同时除一个折减系数K，目的使边坡达到极限破坏状态。经过折减后的滑面参数c'和tanφ' 表达式为：

依照强度折减法原则，将岩质边坡外力所做的功率公式（4-49）和滑面上阻力所消耗的功率公式（4-50），代入虚功率方程（4-43）式中，消除等号两边的应变速度v项，整理后得到岩质边坡的稳定系数计算公式为：

式中：φ'=arctan(φ/K)，由于上式等号右端出现了K，因此式（4-52）是稳定系数的隐式方程，需要通过迭代的算法求解。在计算时，先假设一个初始的稳定系数，应用迭代计算直至前后两次稳定系数值满足所要求的计算精度为止。一般来说对于满足条件的情况，迭代都是收敛的。

4.3.3 楔形体滑移式崩塌计算

不连续面组合的块体形状是多种多样的，可以是楔形体或其他块体，图4-15所以是不连续面可能组合的滑块形状。从图4-15中可以看出，所有楔形体和块体都可能产生运动，但位移有可能沿一个或几个面发生。图4-16中的（a）可以产生运动，而（b）和（c）则不能运动。因此只有运动学上不稳定的岩质边坡，才有必要进一步作分析计算。以下只分析图4-15中的第①、第④和第⑨种情况。

图4-15 楔形体及块体

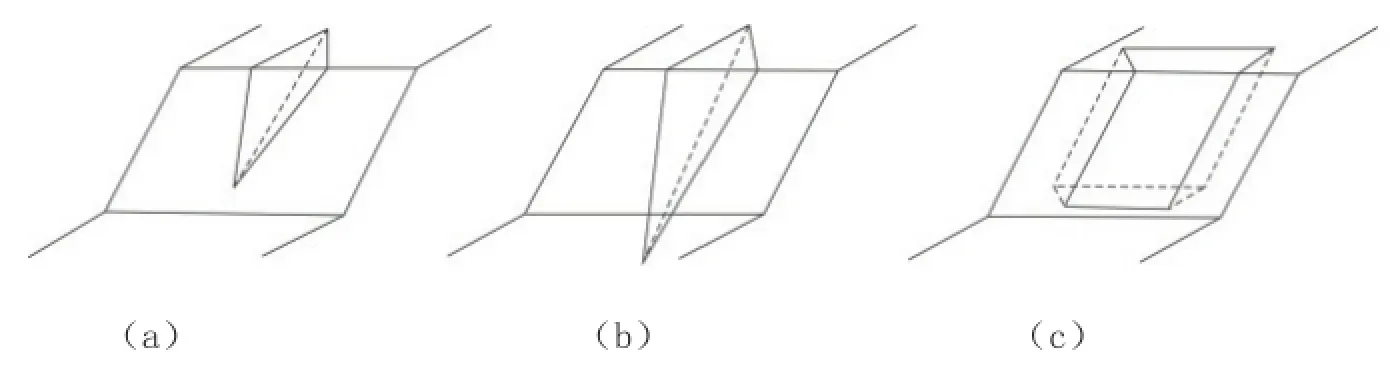
图4-16 （a）可能失稳，（b）和（c）不可能

第9种情况比较简单，滑体只能沿一个面进行运动，在大多数情况下，这种运动是水平方向的。如果除了重力，还有其他作用力，也可能出现旋转运动。对于第4种情况，在下列情况下将出现滑动：①沿一个面出现剪位移或沿一个面出现张位移；②沿两个面出现剪位移；③沿两个面出现张位移。对于第1种情况，下列情况可能出现：①剪位移出现在二个面上，张位移出现在第三个面上；②剪位移出现在一个面上，张位移出现在另两个面上；③张位移出现在三个面上。以下讨论楔形体的稳定性计算方法。

（1）楔形体分析计算

楔形体滑动的滑动面由两个倾向相反、且其交线倾向与坡面倾向相同、倾角小于边坡角的软弱结构面组成，如图4-17所示，ΑBD和BCD两条结构面斜交构成的ΑBCD三角锥，三角锥的高度为H，三角锥的重量以G（kN）表示。

图4-17 楔形体崩塌

不考虑地震作用力、人工爆破和降雨等影响因素，楔形体稳定性系数计算的基本思路:

如图4-18所示，首先将滑体自重G分解为垂直交线BD的分量N和平行交线的分量（即滑动力Gsinβ），然后将N投影到两个滑动面的法线方向，求得作用于滑动面上的法向力N1和N2，最后求得抗滑力及稳定性系数。

可能滑动体的滑动力为Gsinβ，垂直交线的分量为N=Gcosβ。将Gcosβ投影到△ABD和△BCD面的法线方向上，得法向力N1、N2：

楔形体的抗滑力：

楔形体的稳定性系数：

式中：C1，φ1分别为ΑBD结构面和岩桥的黏聚力（kPa）和内摩擦角（°）；C2，φ2分别为BCD结构面和岩桥的黏聚力（kPa）和内摩擦角（°）；S△ΑBD和S△BCD分别为两滑面的面积；当考虑地震和降雨条件时，可能的水平地震力以P=aG（kN）表示，静水压力以U表示，楔形体沿ABD、BCD量结构面滑动，两滑面上的摩擦阻力分别为：(N1-V1-U1)tanφ1，(N2-V2-U2)tanφ2，此时楔形体的抗滑力F抗为

楔形体的稳定系数为

式中：

式（4-56）、式（4-57）及式（4-58）中的N，V和U的物理意义如图4-18所示，其中，V1，V2为作用在两滑面上地震力P的法向分力（kPa）；U1，U2为作用在两滑面上静水压力的法向分力（kPa）。

（2）典型实例分析

以Hoek的著作《Rock Slope Engineering》中的典型楔形体为实例，通过加拿大Rockscience公司开发的Swedge4.0软件，对潜在的崩塌体——三维楔形体稳定性进行分析计算。已知某岩石边坡高度为33m，坡面倾向195°，坡角65°，坡顶面倾向195°，倾角12°。岩体中有两组主要结构面：其中第一组结构面（结构面ΑBD）倾向105°，倾角45°，黏聚力C为23.9kPa，内摩擦角20°；第二组结构面（结构面BCD）倾向235°，倾角70°，黏聚力C为47.9kPa，内摩擦角30°。后缘裂隙面倾向165°，倾角70°。分析计算所用数据详见表4-1。

根据边坡坡面、顶面及岩体结构面产状，作出赤平投影分析图（见图4-19）。根据结构面大圆组合形成的交线与坡面投影以及摩擦园的相对位置和分布情况判断楔形体是否会产生滑动的可能性。判据为：① 结构面大圆组合形成的交线投影位于坡面大圆与摩擦圆之间的月牙形区域；② 交棱线倾向位于坡面倾向与一组结构面倾向之间。若仅满足判据①，则为单面滑动破坏；若同时满足①和②，则为双面滑动破坏（楔形体破坏模式）。

表4-1 楔形体几何要素和特征（E.Hoek）

图4-19 楔形体赤平投影分析图

楔形体稳定性计算时分为无后缘裂隙和有后缘裂隙两种情况（图4-20～图4-25），计算工况选择天然状态、静水压力和地震作用三种。分析计算成果见表4-2，两种情况在天然状态下，楔形体均不会发生滑移式崩塌破坏；在Ⅸ度地震烈度工况下，水平地震影响系数取0.4，两种情况下楔形体均会发生滑移式崩塌破坏；考虑静水压力工况时，第二种情况下如果结构面完全充水也会导致楔形体处于滑动临界状态。

表4-2 楔形体分析计算成果

图4-20 楔形体几何要素分析图（四面体）

图4-21 楔形体几何要素分析图（五面体）

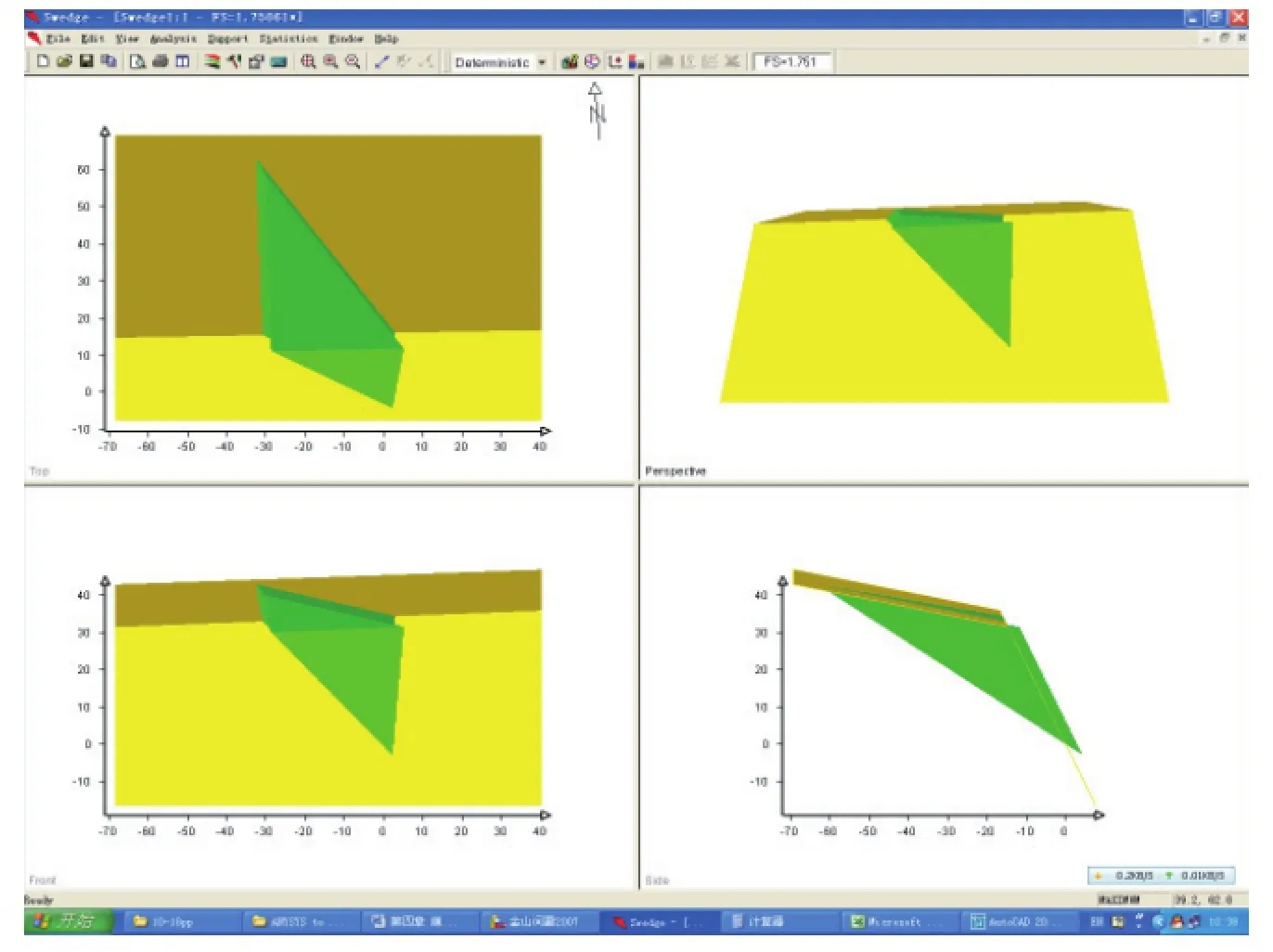
图4-22 楔形体三维阴影图（四面体）

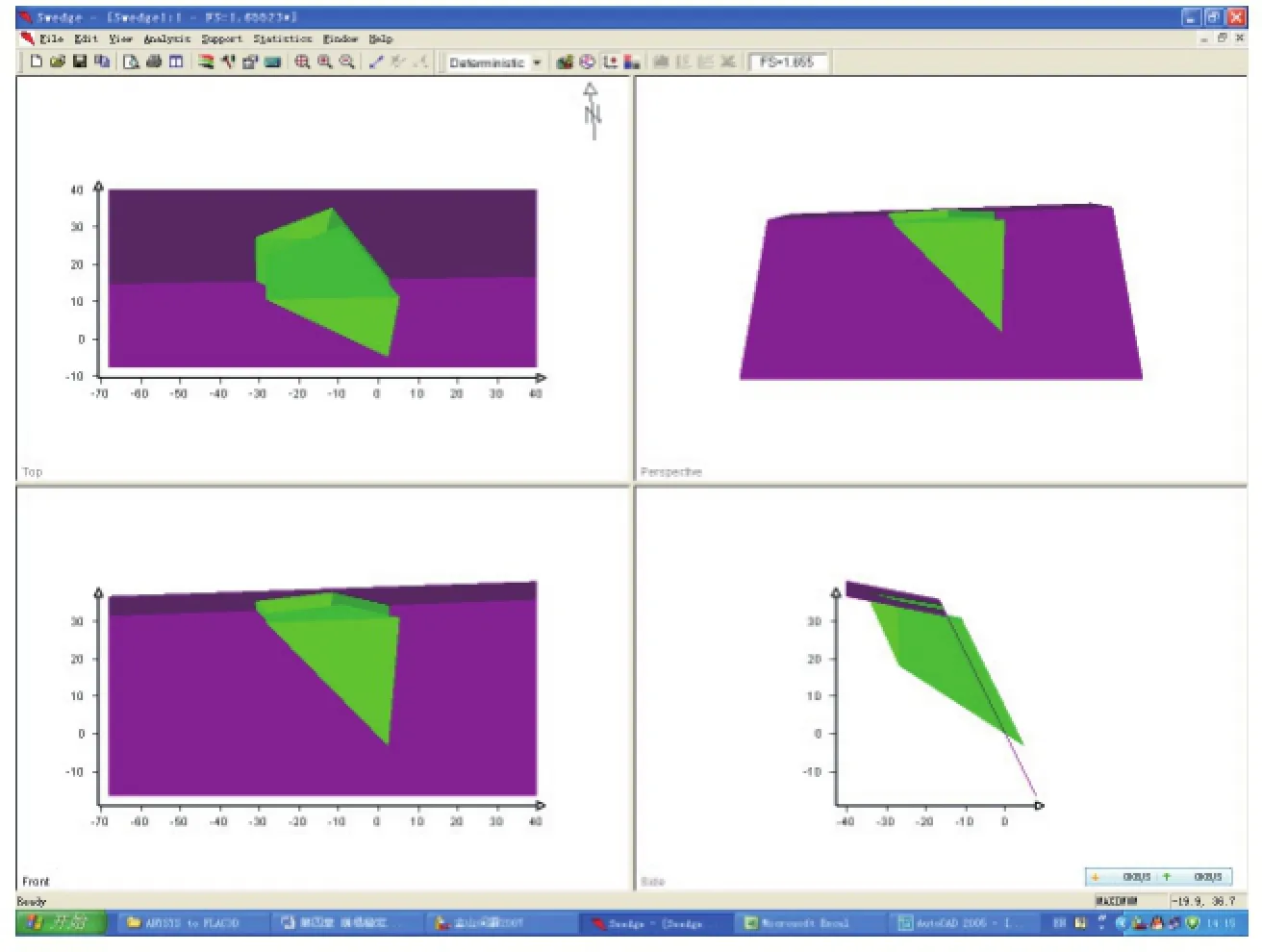
图4-24 楔形体三维阴影图（五面体）

图4-25 楔形体三维立体图（五面体）

4.3.4 局部块体滑移式崩塌计算

局部块体滑移引起的崩塌在公路沿线也比较常见，特别是2009年6月5日，重庆武隆鸡尾山发生的大规模山体崩滑灾害（见图4-26）就属于这一类型。崩滑岩体沿缓倾炭质软弱夹层顺向长期缓慢蠕动，下滑力逐渐增加，致使其北部前缘起阻挡作用的关键块体长期受到挤压，前缘关键块体首先失稳崩塌，其后的崩滑岩体沿“关键块体”失稳，失去“关键块体”支撑的整个山体沿软弱层面产生连锁式的滑动破坏，并迅速解体，形成碎屑流。

图4-26 重庆武隆鸡尾山发生大规模山体崩滑灾害

对于岩质高切坡局部滑动块体，其侧壁效应对稳定性影响非常突出，除滑动面以外，还有两个侧壁和后壁对滑动块体稳定性有影响，侧壁摩擦效应对抗滑力有贡献，后壁若充水则有水压力影响稳定性，若存在未贯通的完整岩石部分，则该未贯通部分的抗拉强度对抗滑稳定性有贡献，必须予以考虑。依据后壁的贯通状况，考虑侧壁效应的稳定性分析，可细分为后壁贯通和未贯通两种情况。

1）后壁完全贯通滑块稳定性计算

当后壁岩层完全贯通的情况下（见图4-27），设滑面的面积为S（m2），后壁面积为S1（m2）。宽度为b（m），左侧壁面积为S2（m2），右侧壁面积为S3（m2），左侧壁结构面黏结力为c2（KPa），右侧壁粘结力为c3（KPa）。

图4-27 后壁完全贯通情况下的边界

（1）自重+天然状态裂隙水压力

相应水压力和稳定系数表达式为

（2）自重+暴雨状态下的裂隙水压力

相应水压力和稳定系数表达式为

（3）自重+天然状态下裂隙水压力+地震力

其裂隙水压力计算同式（6-64）和式（4-65），稳定系数为

2）后壁未完全贯通滑块稳定性分析

当后壁未完全贯通时（见图4-28），稳定性分析需要考虑后壁未贯通部分岩石的抗拉能力对稳定性的影响。设未贯通部分面积为S0（m2），则贯通部分的面积为S1-S0，贯通部分高度为h1=（S1-S0）/b (m)。则统一的各工况稳定系数计算式为

图4-28 后壁未完全贯通模式

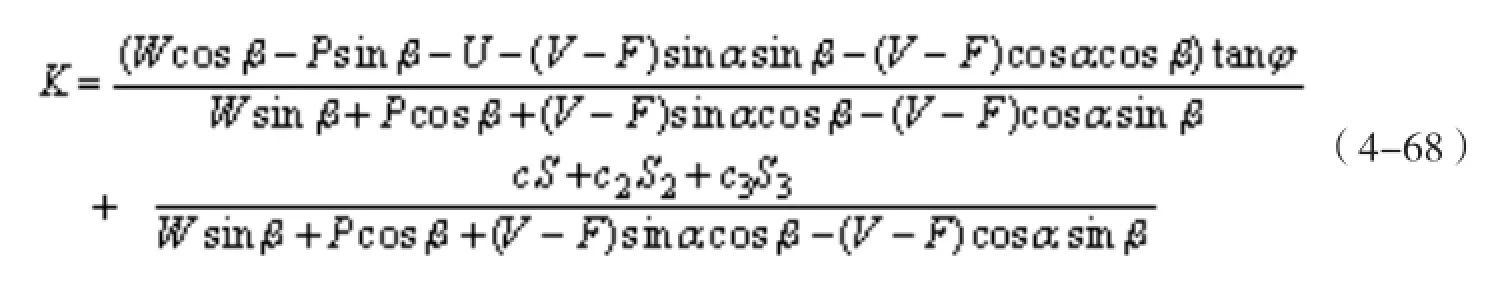
式中：F=σtS0为未贯通部分岩石抗拉力；σt为岩石抗拉强度设计值。对应自重+天然状态下的裂隙水压力或自重+暴雨状态下的裂隙水压力工况，需略去地震力有关项，而且在计算后壁水压力时以h1代替贯通状态下的h进行计算即可；对于自重+天然状态下裂隙水压力+地震力工况水压力计算同其他工况，仅需在公式中保留地震力各项。