分形维数测定方法对测量结果的影响分析

杨 扬，张永海，＊，白宝丰，陈静波，申长雨

（1.郑州大学国家橡塑模具工程研究中心，河南 郑州 450002；2.郑州轻工业学院河南省表界面科学重点实验室，河南 郑州 450002）

0 前言

自从Mandelbrot等提出分形理论以来，无论其在数学基础理论抑或应用研究方面都取得了巨大进步。如今，它己渗透到物理、化学化工、机械工程、材料科学、地质、地震、岩土工程、气候气象学、生物医学、金融经济、社会科学等诸多领域［1］。一般地，描述分形结构这种自相似、不规则程度或破碎程度的定量参数是分形维数（Fractal Dimension），亦称分维、分形维。根据不同的定义，分形维数具有多种测量与计算方法。目前，针对不同的研究对象，已建立了不同的分形维数测定方法，如：盒计数法、面积—周长法、小岛法、二次电子衬度曲线法、Fourier变换法、垂直截面法、小波变换方法、功率谱方法、赫斯特相关指数法、变分法及容量维法等。

虽然盒计法是一种较好的计算二维图像分形维数的方法［2］，但与图像本身所赋予的物理涵义关系不大，且根据分形维数测定原理，我们可以推断出盒计法受观察者本身影响较大，因为若在一个方格子内有一点或多点，则其对测算结果是没有影响的，即方格内点的边界的判断准确与否直接影响网格内总体的点的数量，从而影响分形维数的测定结果。因此，其计算结果的可靠性值得怀疑。

自Mandelbrot等提出用“小岛法”测量马氏体钢断裂表面分形维数值后，由于其具有测算简便且对形状差异不太敏感的优点，因此越来越广泛地被应用于材料断裂研究［3］。尽管不同定义下的分形维数具有不同的物理涵义，其数值也可能存在差异，所以彭瑞东等认为不能简单地比较评价由不同测定计算方法得到的分形维数［2］。但是如果根据研究对象的特点并结合其赋予的具体的物理涵义，结果可能会有所差异。同时，为了保证数据的可比性，辨别不同分形维数的计算方法及其差异，本研究拟利用扫描电子显微镜对粉末PVC／NBR共混型热塑性弹性体拉伸断面形貌进行观察与分析，并基于断面“盒计法”和“小岛周长－面积关系”，测定其试样断口的分形维数，以考察分析通过不同测定方法所得的分形维数之间的差异，揭示分形维数与材料拉伸断面及力学性能之间的内在联系，寻求材料断裂机制。

1 实验部分

1.1 主要原料

PVC，SG－5，山西榆社化工股份有限公司；

轻钙（CaCO3），三型，焦作市三耀化工有限公司；

稀土复合稳定剂，工业级，南京惠恩实业有限公司；

NBR，P83，市售；

增塑剂（DOP），工业级，市售；

硬脂酸（HSt），工业级，市售。

1.2 主要设备及仪器

高速混合机，GH－10，北京塑料机械厂；

平板硫化机，QLBD－400×400×1000，上海橡胶机械厂；

开放式炼塑机，SK－160B，上海橡胶机械厂；

电子万能试验机，CMT6104，深圳新三思计量技术有限公司；

橡胶硬度计，LX－A，上海第六中学量仪实验工厂；

扫描电子显微镜（SEM），JSM－5600L，日本电子株式会社。

1.3 样品制备

粉末PVC／NBR共混型热塑性弹性体试样制备工艺分为以下3个步骤：（1）高速混合过程；（2）双辊塑炼过程；（3）压制成型过程。其总体成型工艺路线如图1所示，图2为其拉伸断面SEM照片。

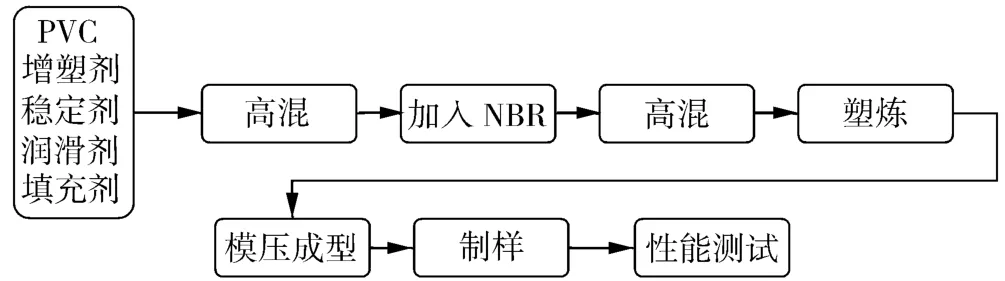
图1 PVC／NBR弹性体试样制备工艺路线Fig.1 Preparation process of PVC／NBR elastomer samples

高速混合过程：先将高速混合机预热至70～90℃时，将PVC与稳定剂、润滑剂一同放入高速混合机，然后将增塑剂DOP分3批加入，混合均匀（10min）后加入NBR继续混合5min出料；

双辊塑炼过程：辊温控制在125～135℃之间，前辊较后辊温度高5℃左右；辊距1～115mm，整个塑炼过程保持8min左右；

压制成型过程：模温控制在145～155℃之间，首先对片料预热8min，以使片料受热充分均匀，然后加压3min，压力控制在10～15MPa之间；

1.4 性能测试与结构表征

塑料样品测试状态调节和试验条件按GB／T 2918—1998执行；

热塑性塑料压塑试样的制备方法按GB 9352—1988执行，拉伸速率为50mm／min；

塑料试样拉伸性能试验方法按GB／T 1040—1992执行，弯曲速率为5mm／min；

塑料试样弯曲性能测试方法按GB／T 9341—2000执行。

2 分形维数测定基本原理

按照分形理论，分形系统或结构从各个时空角度来看都是相似的［4］，即其局域性质或结构与其整体具有相仿、相似的特性。但对于这种相仿、相似性，若分形系统或结构是按照某种一定的数学规则生成的，则其具有严格的自相似性，属于有规分形；若其是仅限于满足物理统计意义上的自相似性，则不具有严格的自相似性，属于无规分形。自然界里的分形，大多属于后者。对于上述两种分形，其重要衡量参数——分形维数有类似的计算方法，其中最具代表典型性的是Hausdoff维数。其定义为：对于任意一个满足自相似

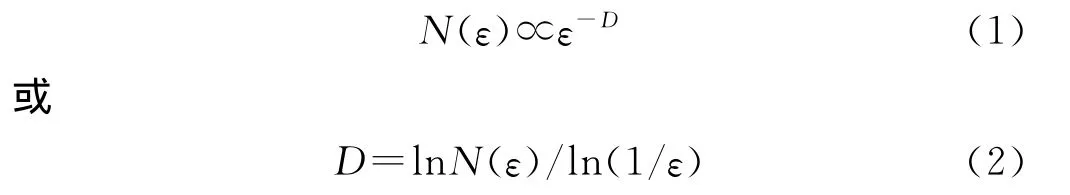
式中 D——Hausdoff维数，可以是整数亦或分数，若平面上关注的点均匀且致密地排列并覆盖住整个平面，则D＝2

一般地，测定分形维数的方法可分为如下5大类［5］：（1）变尺度法；（2）测度关系法；（3）相关函数法；（4）分布函数法；（5）频谱法。其中第一种方法即变尺度法是最常用且有效的。在实际计算时，一般采用如下计算步骤：

首先，用标尺为ε的方格把平面图形分割成边长为ε的正方形，然后测量出此平面图形上至少包含一个点的正方形的个数N（ε）。若当ε取不同的大小时，上式（1）成立，则D就是平面图形上点的分形维数。

此外，存在争议最多、应用最广泛的小岛法（亦称周长－面积法）也是一种计算分形维数的方法。其定义为：

首先，对于如三角形、正方形和圆形等规则图形，规则图形的周长（P）和面积（A）之间具有以下关系［6］：

其次，对于如自然界中海岛、天空中的云彩、材料中显微组织结构分布等满足具有物理统计自相似特性的不规则图形的周长P和面积A之间具有以下关系：

式中 D——不规则图形的分形维数

为计算方便，对式（4）两边取对数，则有

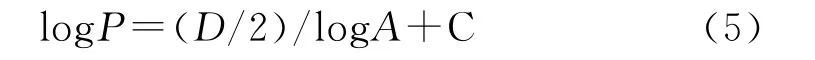
式中 C——常数

由此可知，分形维数D相当于由关注点的周长与面积取对数后在坐标上所拟合的直线的斜率的2倍。

3 结果与讨论

3.1 SEM照片分析

为了增加实验数据的对比性，首先在未加粉末NBR时测试出有关数据。然后加入粉末NBR进行实验。实验结果的SEM照片如图2所示。

由图2（a）可知：由于无橡胶相，可明显地看到拉伸断面为连续的PVC基体树脂相。当加入NBR时，在PVC连续相中存在许多的白色颗粒状轻钙粒子，稍大一点的细胞或类似细胞状的为丁腈橡胶。如再仔细观察可发现：样品中NBR没有以颗粒状的形式分散于PVC基体连续相中，而是包覆了PVC粒子后以间断分散相的形式存在于连续相PVC基体中，呈现出海中有岛，岛中有海的“海－岛”互穿网络组织结构。混合界面之间具有明显的自相似性，在研究的微米度域范围内可以认为其具有分形结构。

3.2 分形维数测定方法分析

分形维数是分形系统或结构复杂程度的一种测度，反映了分形系统或结构与其所在空间的份量多少，其值越大，表明分形系统或结构所占空间的比例越大。因此分形维数测量结果的可靠性与准确性直接影响着我们对实验结果的判断与分析。在分形损伤断裂的研究中，人们一开始就尝试着根据材料断裂表面的分形维数来研究其断裂演化过程与断裂机理，并期望建立断裂表面的分形维数与宏观力学性能之间的关系。由此可见，分形维数对人们认识断裂过程及断裂机理具有至关重要的作用。因此，分形维数测量结果的可靠性与准确性日益引起了人们的广泛关注。

然而，分形维数值的测定需要经过许多纷繁复杂而精细的工作，具体到特定断裂表面SEM图像并采用盒计法测定分形维数时，需要将图像划分为边长为ε的网格，然后前述方法求出分形维数。

根据测量计算过程可知：采用盒计法测定的分形维数反映了由离散、随机点构成的图形中所主要的关心区域在全部视域内的分布特征［2］。但由于除了断裂裂纹在SEM图像上的分布通常是随机的，并且是离散的。当取边长为ε的网格把断裂表面SEM图像覆盖起来后，因其内部裂纹分布的随机性、偶然性，会造成有些网格内是空的，而有些网格内则覆盖了分形裂纹的一部分，尤其是如果在一个网格内有一个点与多个点时，在计算总的网格个数N（ε）时具有同样的权重。再者，若方格内点的边界正处于网格的边界，则网格内的点的数量的判断准确与否就会影响最终的分形维数测定结果。如图3所示，两个明显不同的图形在计算网格内覆盖的点的个数N（ε）时，其值均为9。这样，网格内覆盖的点的个数就未反映出几何对象的不均匀分布性。因此，采用盒计法具有一定的局限性。但对于我们的研究对象——PVC／NBR弹性体断裂表面由于具有明显的“海 －岛”组织结构，故采用 Mandelbrot等提出的小岛法应该具有较明显的优势：能够精细地反映图案的细节变化与不均匀分布性，采用该方法所得到的分形维数值应该比盒计法可靠性强。

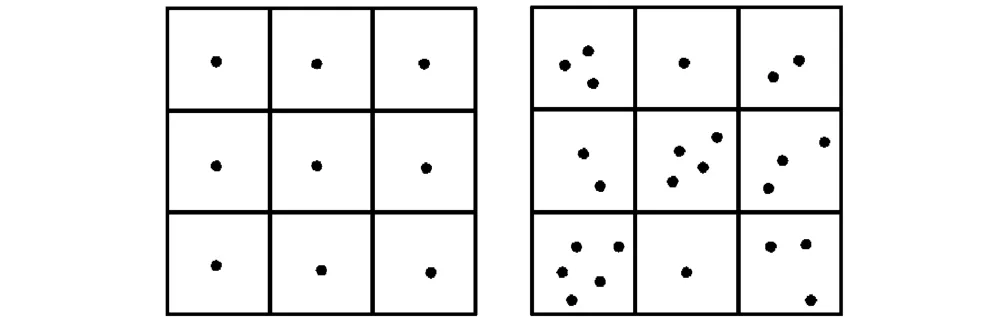
图3 盒计法网格单元内覆盖点个数的比较Fig.3 Comparison of the number of covering body by box－counting method

3.3 分形维数的测定

按照Mandelbrot等提出的小岛法，即前面所述的“周长－面积关系”计算出图2中各SEM照片的分形维数。其计算过程为：首先将SEM照片输入计算机，利用Image－Pro Plus图形分析软件，测量出每个“岛”的周长和面积，如图4所示。然后根据式（5）在双对数坐标上画出logP和logA，如图5所示，此时可以发现所得结果具有较好的线性关系，表明断裂表面确实具有分形特性。采用最小二乘法拟合出该直线，该直线斜率的2倍即为分形维数D。最后，分形维数的测定结果如表1所示。为对比盒计法的测定结果，这里同时列出这两种测定方法的结果。

图4 周长与面积的测定Fig.4 Determination of the perimeter and area

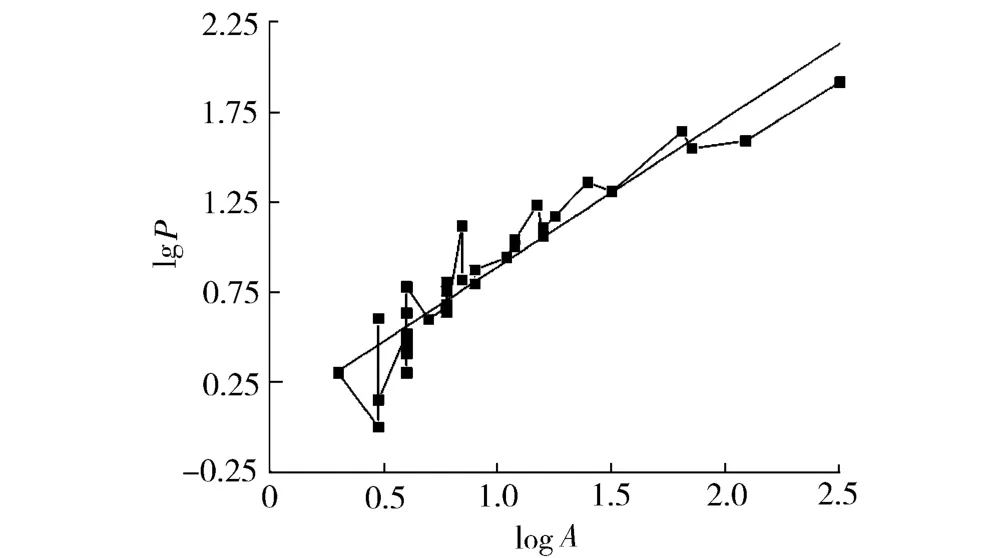
图5 小岛法数据的拟合Fig.5 Data fitting by slit-island method

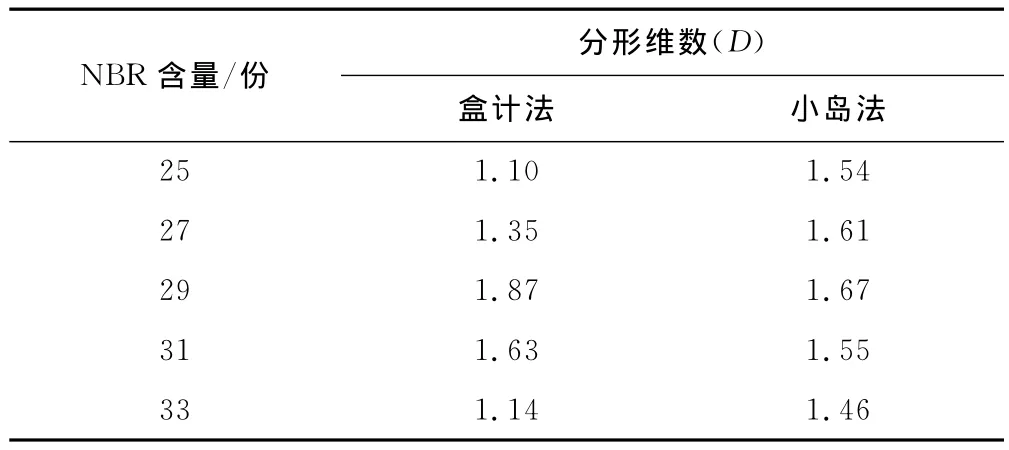
表1 采用不同方法获得的分形维数值比较Tab.1 Comparison of fractal dimension calculatd by various methods

与盒计法所得结果相比，可以看出：采用小岛法所测得的分形维数在丁腈橡胶NBR含量较低时，其值较大，随着NBR含量的增加，其变化范围明显较小。但其两者变化规律相同：均呈先逐渐上升后下降趋势，表明与盒计法所测得的分形维数反映的材料断裂规律一致：PVC／NBR弹性体断面的分形维数与材料力学性能（拉伸强度、断裂伸长率、肖氏硬度）变化关系一致［4-7］。这种现象可能源于下述原因：

采用盒计法在计算“岛”或“湖”个数N（ε）时，由于某些网格内可能会占有较多的的“岛”，而某些网格内可能会占有较少的的“岛”，这样其个数N（ε）会把占有较少“岛”的网格也计算在内，忽略了网格内小岛多少的差异，从而导致N（ε）较大，而采用小岛法时，根据其分形维数测定原理，其只会计算“岛”的面积和周长，不会牵涉至网格内“岛”的个数问题，所以其计算结果较小，也更加可靠。另一方面，也从侧面验证了Mandelbrot等提出的用“面积－周长法”（即小岛法）测量马氏体钢断裂表面分形维数值的正确性。

根据以上分析可知，虽然盒计法较成熟，但也存在缺陷：在具体用于描述研究对象计算总的网格个数N（ε）时，缺乏考虑权重因子。尽管如此，根据我们的分析可以知道，在揭示材料组织结构评价、探索材料断裂演化规律方面，两者所得结果一致，并无差别。此外，在使用分形维数阐释、揭示研究对象的分形特性，尤其应用于材料组织结构与断裂演化规律、分形形成的动力学机制时，为更真实准确地反映其物理本质，首先且重要的是分析考察研究对象的分布特点，然后再选择恰当的、合适的分形维数测定方法，最后再考察分形维数与相应物理现象的关联性。

4 结论

（1）采用盒计法和小岛法所测得的分形维数反映的材料断裂规律一致：PVC／NBR弹性体断面的分形维数与材料力学性能（拉伸强度、断裂伸长率、肖氏硬度）变化关系一致；

（2）为更真实准确反映材料组织结构与断裂物理本质，需首先分析考察研究对象的分布特点，然后再选择恰当的、合适的分形维数测定方法。

［1］张永海.基于分形理论的聚合物基复合材料断裂评价研究［D］.郑州：郑州大学材料科学与工程学院，2011.

［2］彭瑞东，谢和平，鞠 杨.二维数字图像分形维数的计算方法［J］.中国矿业大学学报，2004，33（1）：19－24.Peng Ruidong，Xie Heping，Ju Yang.Computation Method of Fractal Dimension for 2－D Digital Image［J］.Journal of China University of Mining ＆ Technology 2004，33（1）：19－24.

［3］任文伟，康戈文，甘春泉，等.锆－4合金疲劳断口的分形维数分析［J］.稀有金属材料与工程，2006，37（10）：13－16.Ren Wenwei，Kang Gewen，Gan Chunquan，et al.Analysis of Fractal Dimension for Fatigued Fracture of Zircaloy－4 ［J］.Rare Metal Materials and Engineering 2006，37（10）：13－16.

［4］张永海，白宝丰，申长雨，等.粉末NBR－PVC共混型热塑性弹性体断裂面的分形维数［J］.高分子材料科学与工程，2009，25（1）：55－58.Zhang Yonghai，Bai Baofeng，Shen Changyu，et al.Fractal Dimension of Powder NBR－PVC Blend TPE Fracture Surfaces［J］.Polymer Materials Science ＆ Engineering 2009，25（1）：55－58.

［5］张济忠.分形［M］.北京：清华大学出版社，1995：111－121.

［6］卢春生，白以龙.材料损伤断裂中的分形行为［J］.力学进展，1990，20（4）：468－477.Lu Chunsheng，Bai Yilong.Fractals In Damage And Fracture of Materials［J］.Advances In Mechanics 1990，20（4）：468－477.

［7］张永海，白宝丰，王 涛，等.分形理论在PVC／粉末NBR共混研究中的应用［J］.中国塑料，2007，21（12）：29－32.Zhang Yonghai，Bai Baofeng，Wang Tao，et al.Application of Fractal Theory in the Study of PVC／Powder NBR Blending Interface［J］.China Plastics，2007，21（12）：29－32.