J2项和大气阻力摄动作用下卫星编队构型的演化分析

黄 勇 李小将 王志恒 李兆铭

装备学院研究生院，北京 101416

微小卫星技术的迅速发展，使得卫星编队飞行日渐成为国际航天领域的一个研究热点。它是指多颗卫星在自主运行的同时，彼此间相距较近且保持某种特定的空间几何构型，通过星间链路相互通信、密切协同，共同完成某项空间任务(如对地观测、立体成像、电子侦查等)[1]。卫星编队飞行的特点及卫星间的有效协作，要求编队卫星间的相对位置和相对轨道维持稳定。而实际上卫星在轨运行的过程中，会受到多种空间摄动的影响，必然导致卫星编队构型发生变化。因此，须对卫星编队构型在相关摄动作用下的演化进程进行分析，从而为编队构型的设计、保持与重构提供理论依据和参考。

目前，分析空间摄动对卫星编队构型的影响主要集中于2种方法：1)基于C-W方程的分析方法。文献[2]提出了一组考虑J2项摄动的线性微分方程，形式类似于C-W方程但精度更高；文献[3]将J2项摄动以力函数的形式加入到C-W方程右端，得到了适用于分析摄动长期影响的相对运动方程，并给出了近似的解析解；文献[4]将相对运动方程中引力作用的非线性项和参考星的偏心率视为导致C-W误差的2种摄动，结合J2项摄动，得到了可描述椭圆参考轨道和包含J2项摄动的C-W方程，并以状态方程的形式表现出来。2)基于轨道根数的摄动分析法。文献[5]分析了大气阻力摄动对卫星编队构型的影响，得到了不同初始相位环绕星的长半轴摄动方程，并提出了补偿大气阻力摄动影响的长半轴修正方法；文献[6]采用相对轨道根数法推导出了包含大气阻力摄动的卫星编队相对运动的状态转移方程，得到了大气阻力摄动主要影响编队构型沿航迹方向相对距离的结论；文献[7]把用状态转移法获得的卫星编队相对运动分析解表达成无奇点轨道根数形式，分析了J2项摄动下构型的长期演化机理，并推导出了解析表达式；文献[8]利用J2项摄动下顺根与平根的转化，建立了基于初始轨道根数和瞬时轨道根数差的参考轨道为椭圆的编队相对运动方程，分析了J2项摄动对编队构型的长期影响。但随着研究的深入，2种方法的利弊也逐渐显现。方法1便于理论分析，且由于该方法可以获得相对运动方程的解析解，故计算耗时短。但该方法在相对运动方程的建模过程中误差较大且使方程成立的前提条件较多，不适宜描述卫星编队的长期飞行[9]。方法2没有考虑轨道为圆轨道和星间距离足够小的限制，便于研究摄动对构型的影响。但该方法中变量的几何和物理含义不明晰，计算过程较繁琐。

本文从卫星编队飞行的相对运动动力学模型出发，分别将J2项摄动、大气阻力摄动考虑进去，对卫星编队在这2种摄动的综合作用下构型的演化情况进行分析。由于该方法没有经过任何简化和线性化处理，故可以得到很高精度的解，且得到的动力学方程便于今后的编队队形控制研究。

1 卫星编队飞行相对运动动力学模型

1.1 坐标系定义

考虑卫星编队飞行相对运动动力学分析过程中涉及2颗卫星，即参考星和环绕星，研究相对运动动力学模型采用如下2个坐标系：

1)地心赤道坐标系(OXYZ)：坐标原点位于地心O，以赤道面为基准面，OX轴指向平赤道面上的平春分点，OZ轴垂直于平赤道面指向北极，OY轴与OX轴、OZ轴构成右手坐标系。通常将地心赤道坐标系视为地心惯性坐标系，本文采用J2000地心赤道坐标系；

2)Hill坐标系(oxyz)：坐标原点位于参考星的质心o，ox轴沿地心与参考星质心的连线背向地心，oy轴在轨道平面内垂直于ox轴并指向参考星运动方向，oz轴与ox轴、oy轴构成右手坐标系。通常将oy轴方向称为沿航迹方向，oz轴方向称为垂直于航迹方向。Hill坐标系是一种RTN坐标系(即径向、航向、法向坐标系)，在相对运动动力学分析中应用广泛，它与地心赤道坐标系的关系如图1所示。

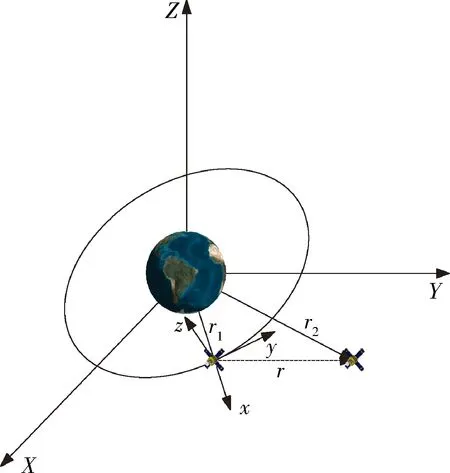
图1 地心赤道坐标系和Hill坐标系

1.2 相对运动动力学模型

参考星和环绕星在地心惯性坐标系中的位置矢量分别用r1和r2表示，则环绕星相对参考星的相对位置矢量为：

r=r2-r1

(1)

参考星和环绕星在地心惯性坐标系下的轨道动力学方程可以表示为：

(2)

(3)

式中，μ为地球引力常数，r1和r2分别为参考星和环绕星的地心距，f表示除地球引力之外的所有摄动力和控制力引起的加速度之和。

根据式(1)～(3)，可以推得：

(4)

式(4)为地心惯性坐标系中环绕星相对参考星的相对运动动力学方程，其中两星的运动状态是随时间不断变化的，故式(4)为一个非线性时变系统。若基于以下3点假设：地球为理想球体、参考星运行于标准圆轨道及参考星与环绕星相对距离足够近，可将式(4)转换到Hill坐标系中进行线性化并忽略二阶小量，得到相对运动的分量形式如下：

(5)

式中，n为参考星平均轨道角速度，x，y，z为环绕星在参考星Hill坐标系中的相对位置分量，fx，fy，fz为除地球引力之外两星所有摄动力和控制力引起的加速度之和在Hill坐标系中的分量。式(5)即为著名的C-W方程(亦称Hill方程)，在不考虑摄动力和控制力的作用下，可以得到其解析表达式。由于解析模型形式简单、表达清晰，便于定性、定量的分析和控制律的设计，故C-W方程广泛应用在航天器近距交会对接和卫星编队飞行的研究初期。但是，C-W方程成立的3点假设、线性化过程中的建模误差以及空间摄动因素的忽略限制了其在卫星编队飞行问题中的进一步应用。

2 J2项摄动和大气摄动对卫星编队飞行的影响分析

二体假设下，长半轴相等的卫星间的相对运动构型可以保持自然长期稳定。实际上，空间存在多种摄动因素，如地球非球形、大气阻力、日月三体和太阳光压摄动，这些摄动将破坏卫星编队的相对运动构型。根据文献[10]，不同的摄动对卫星在轨运行影响的量级不同，具体的差异见图2。

图2 不同高度摄动力影响分布图

从图2可以看出，地球非球形摄动是卫星所受空间摄动的主要来源。而大气摄动属于非保守力引起的摄动，其对近地轨道卫星编队相对运动的长期影响不容忽视。三体摄动和太阳光压摄动对卫星相对运动的影响很小，可以忽略，本文对此也不予探讨。

2.1 J2项摄动对卫星运动的影响

二体条件下，地球被理想化为一个均质球体，地球对卫星的作用力只有中心引力。而实际上地球并非球对称，质量分布也不均匀，而是具有扁平度的梨形椭球体，导致地球重力场分布不均匀。故卫星在轨道的切线方向和法线方向同样受到引力作用，将这些额外的力学因素统称为地球非球形摄动[11]。因此，需在地球引力场位函数中增加一系列球面调和函数，以表示地球引力等位面与等球面的不重合。

目前广泛采用的地球引力场位函数U可表示为地心距R、地心纬度φ和地心经度λ的函数[12]：

(6)

式中，Re为地球平均半径；Pn(x)，Pnm(x)分别是勒让德多项式和缔和勒让德函数；Jn为带谐项系数，对应的项为带谐项；Cnm，Snm为田谐项系数，对应的项为田谐调和项。

对于近地轨道卫星，带谐项的影响远大于田谐项，而带谐项系数中属J2最大，其它系数与其相比均为小量。因此，本文仅考虑J2项摄动对卫星编队飞行的影响，可将式(6)简化为：

(7)

考虑J2项摄动后，在地心惯性坐标系中，单颗卫星的运动方程为：

(8)

(9)

给定卫星的初始位置和速度后(或卫星的初始轨道根数)，可利用数值积分法对式(9)进行求解，从而得到J2项摄动作用下单颗卫星运行轨道的演化进程。

2.2 大气阻力摄动对卫星运动的影响

除J2项摄动外，大气阻力是影响近地轨道卫星编队构型稳定的另一种重要的摄动力，其引起的单颗卫星加速度值为[13]：

(10)

式中，CD为大气阻力系数；A为卫星的迎风截面积；m为卫星质量；ρ为大气密度；vrel为卫星相对于当地大气的速度，可通过式(11)求得。其中，R为卫星在地心惯性坐标系中的位置矢量，ω为地球的自转角速度，方向指向Z轴正向，大小为7.29211515×10-5rad/s。

(11)

计算大气阻力摄动引起的加速度，需要确定大气模型。在简单的轨道分析与计算中，常采用指数函数大气密度模型[14]：

ρ=ρ0e-(R-R0)/H

(12)

式中，ρ0为参考点大气密度；R0为参考点高处的地心距；H为密度标高。

仅考虑大气阻力摄动，在地心惯性坐标系中，单颗卫星的运动方程为：

(13)

给定卫星的初始位置和速度后(或卫星的初始轨道根数)，同样可利用数值积分法对式(13)进行求解，从而得到大气阻力摄动作用下单颗卫星运行轨道的演化进程。

2.3 综合J2项摄动和大气阻力摄动对卫星编队飞行的影响分析

结合式(9)和式(13)，可得单颗卫星在J2项摄动和大气阻力摄动共同作用下的运动方程为：

(14)

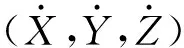
Rrel=(X2-X1,Y2-Y1,Z2-Z1)

(15)

(16)

利用参考星的位置和速度，可以计算出其在各个时刻的轨道根数，从而可以得到地心惯性坐标系到Hill坐标系的转换矩阵，将参考星与环绕星之间的相对运动转换到Hill坐标系中。

r=R(ω)R(i)R(Ω)R(θ)Rrel

(17)

v=R(ω)R(i)R(Ω)R(θ)Vrel

(18)

其中，坐标转换矩阵的具体表示如下：

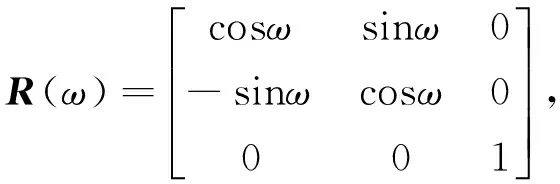
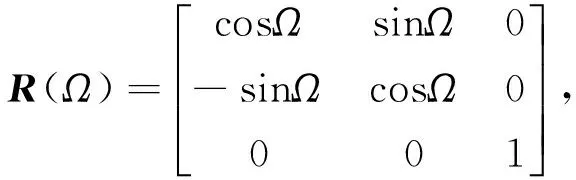
3 仿真分析

下面对J2项摄动作用下、大气阻力摄动作用下以及J2项和大气阻力摄动综合作用下卫星编队构型的演化过程进行仿真分析。编队卫星的相关设计参数参考德国与加拿大合作的TECSAS项目中的航天器，见表1，该项目主要是为空间在轨服务所需的一系列软、硬件技术提供验证。尽管TECSAS项目最终没有正式实施，但项目中航天器的相关设计参数却是研究卫星编队飞行的理想参考。以椭圆编队构型为约束，设定参考星和环绕星的初始轨道参数如表2所示。仿真中所涉及的常量取值如下：地球引力常数μ=398600km3/s2，地球平均半径Re=6378.14km，带谐项系数J2=0.00108263。

表1 编队卫星相关设计参数

表2 卫星编队飞行初始轨道参数

仅考虑J2项摄动，仿真时间t=36000s(卫星轨道周期T=5370.3s，即卫星运行6.7个周期)，卫星编队构型的演化进程如图3所示。由图可见，J2项摄动的存在使编队构型的相对运动轨道面略有转动，且在x-y，x-z和y-z平面内都产生不同程度的漂移。具体到Hill坐标系中的3个方向上，编队中参考星和环绕星的相对运动位置在仿真时间内的漂移量如图4所示。

图3 J2项摄动作用下卫星编队构型的演化

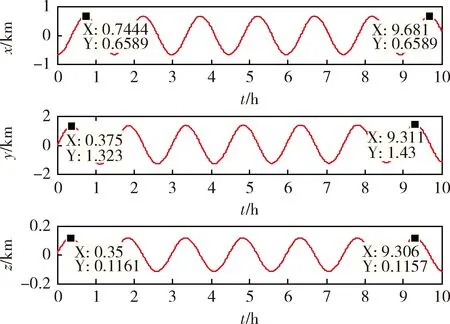
图4 J2项摄动作用下卫星编队相对运动位置变化

仅考虑大气阻力摄动，相同的仿真时间内，卫星编队构型的演化进程如图5所示。由图可见，大气阻力摄动对编队构型的影响较小。因为有研究表明：当编队卫星姿态与面质比相差不大时(参考星面质比为0.01268，环绕星面质比为0.01)，大气阻力摄动对于相对运动的影响是很小的[7]。从图6中的卫星编队相对运动位置变化中可见，大气阻力摄动对两星相对运动位置的影响主要体现在y方向(即沿航迹方向)上，而对z方向和x方向上(即垂直于航迹方向的平面内)的相对运动位置影响甚微。若将环绕星的迎风截面积夸大为50m2，则可清晰地看出大气阻力摄动对卫星编队构型的影响，如图7所示。

图5 大气阻力摄动作用下卫星编队构型的演化

图6 大气阻力摄动作用下卫星编队相对位置变化

图7 大气阻力摄动作用下卫星编队构型的演化(迎风截面积放大后)

综合考虑J2项摄动和大气阻力摄动，卫星编队构型的演化进程如图8所示。从图9中可见，环绕星相对于参考星在x方向和y方向上的最大相对距离逐渐增大，而在z方向上的最大相对距离逐渐减小，但最主要的还是相对位置在y方向上的长期漂移，这与文献[15]的研究结论是一致的。且就空间中的最大相对距离而言，在上述2种摄动的综合作用下，环绕星距离参考星的最大相对距离是逐渐发散的，如图10所示。

图8 J2项和大气阻力摄动作用下卫星编队构型的演化

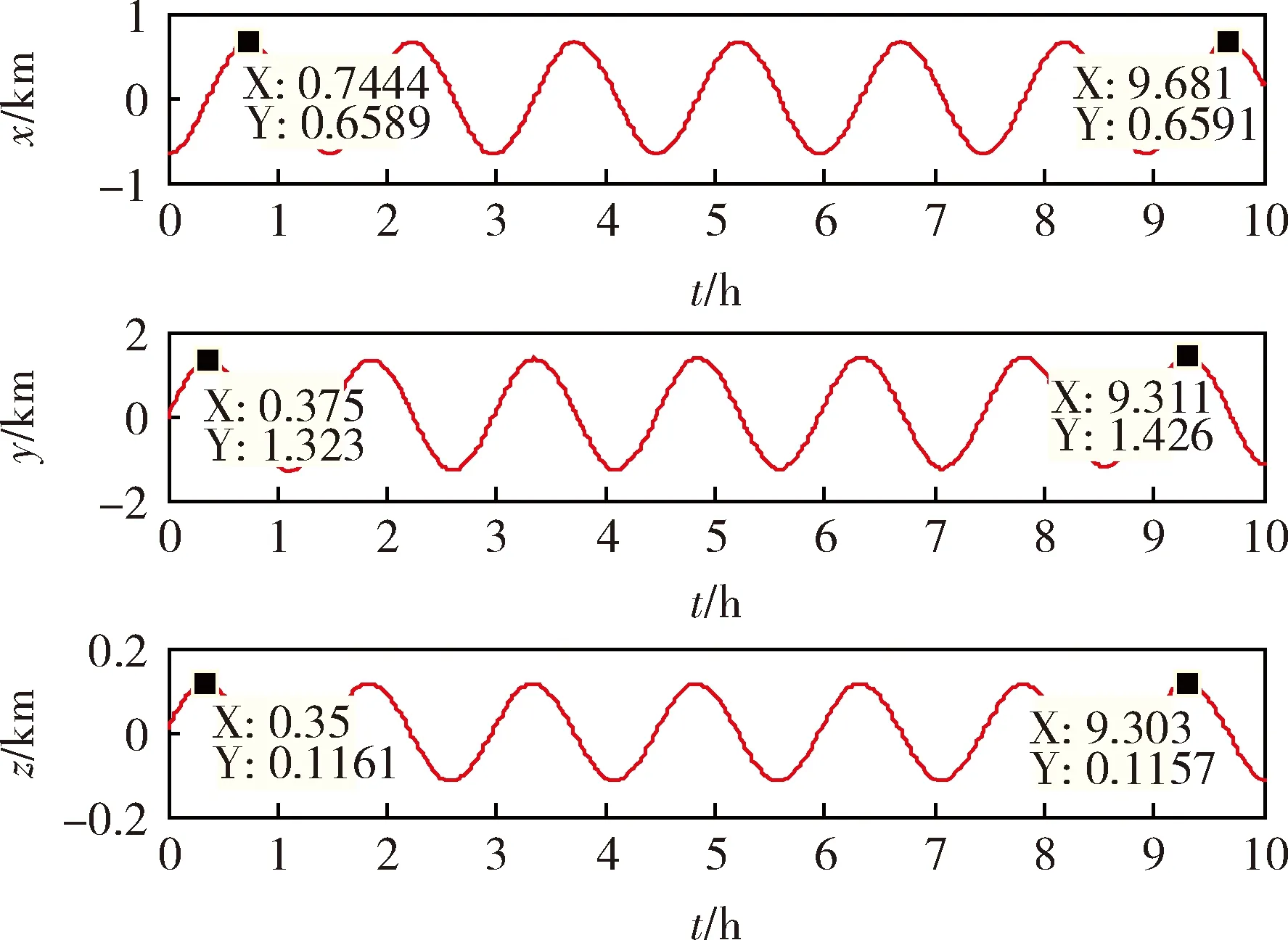
图9 J2项和大气阻力摄动作用下卫星编队相对位置变化

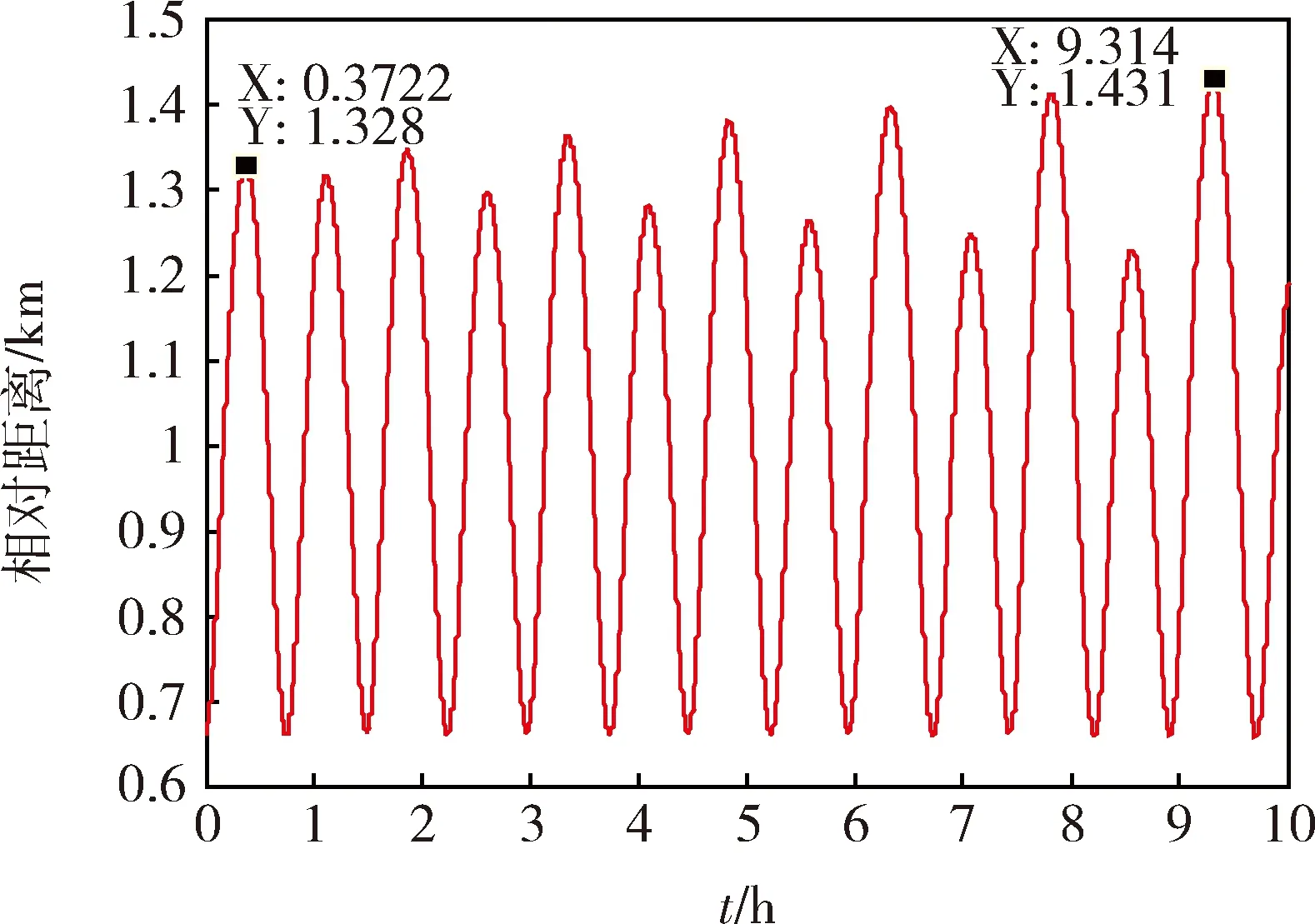
图10 环绕星相对于参考星的距离随时间的变化

4 结论

通过分析卫星编队在J2项摄动、大气阻力摄动以及这2种摄动的综合作用下构型的演化进程，可以得出以下结论：

1)近地轨道卫星所受到的众多空间摄动中，地球非球形摄动中的J2项对卫星编队构型的影响是最主要的。其对卫星编队构型的影响体现在2方面：①相对运动轨道面的空间转动；②相对运动轨道面产生的整体漂移。

2)大气阻力摄动对卫星编队构型的影响主要是导致沿航迹方向的相对漂移。但当编队卫星的面质比较小且相互间差别不大时，大气阻力摄动对卫星编队构型在较短时间段内的影响可以忽略不计。

但这些摄动并非不可利用，例如可以利用大气阻力摄动顺势而为之，实现对编队卫星的气动控制等，这可作为下一步的研究工作。

参 考 文 献

[1] 张玉锟, 戴金海.考虑J2项摄动的卫星编队飞行[J].国防科技大学学报, 2002, 24(2):6-10.(Zhang Yu-kun, Dai Jin-hai.Satellite Formation Flying withJ2Perturbation[J].Journal of National University of Defense Technology, 2002, 24(2):6-10.)

[2] Schweighart S A, Sedwick R J.High Fidelity LinearizedJ2Model for Satellite Formation Flight[J].Journal of Guidance, Control, and Dynamics, 2002, 25(6):1073-1080.

[3] Sedwick R J, Miller D W, Kong E M C.Mitigation of Differential Perturbation in Clusters of Formation Flying Satellites[J].AAS/AIAA Space Flight Mechanics Meeting, American Astronautical Society, AAS Paper 99-124, Feb.1999.

[4] Sangjin Lee, Sang-Young Park.Approximate Analytical Solutions to Optimal Reconfiguration Problems in Perturbed Satellite Relative Motion[J].Journal of Guidance, Control, and Dynamics, 2011, 34(4):1097-1111.

[5] 黄卫东, 张育林.分布式卫星轨道构型的大气摄动分析及修正方法[J].宇航学报, 2005, 26(5):649-652.(Huang Wei-dong, Zhang Yu-lin.Analysis of Atmospheric Perturbation to Distributed Satellites Orbit Configuration and Its Modified Method[J].Journal of Astronautics, 2005, 26(5):649-652.)

[6] 吴宝林, 曹喜滨.大气阻力摄动对卫星编队飞行队形的影响分析[J].航天控制, 2006, 24(1):19-23.(Wu Baolin, Cao Xibin.The Analysis of the Effects on Satellite Formation Caused by Drag Perturbation[J].Aerospace Control, 2006, 24(1):19-23.)

[7] 孟云鹤, 韩宏伟, 戴金海.J2摄动作用下近地轨道卫星编队构型长期演化机理分析[J].宇航学报, 2007, 28(2):253-258.(Meng Yun-he, Han Hong-wei, Dai Jin-hai.Analysis of LEO Satellite Formation Secular Evolvement withJ2Effect[J].Journal of Astronautics, 2007, 28(2):253-258.)

[8] 潘立公, 冯祖仁, 刘建平等.J2摄动影响下椭圆参考轨道的相对运动模型研究[J].系统仿真学报, 2011, 23(4):585-589.(Pan Li-gong, Feng Zu-ren, Liu Jian-ping.Study on Relative Motion Model of Elliptical Reference Orbit Under Influence ofJ2Perturbation[J].Journal of System Simulation, 2011, 23(4):585-589.)

[9] 李俊峰, 雪丹.编队卫星相对运动描述方法综述[J].宇航学报, 2008, 29(6):1689-1694.(Li Jun-feng, Xue Dan.Review of Relative Motion Description Methods for Satellite Formation Flying[J].Journal of Astronautics, 2008, 29(6):1689-1694.)

[10] Esten Ingar Grøtli.Modeling and Control of Formation Flying Satellites in 6 DOF[R].Trondheim, Norway: Norwegian University of Science and Technology, October 2005.

[11] 李俊峰, 孟鑫, 高云峰,等.J2摄动对编队飞行卫星相对轨道构型的影响[J].清华大学学报(自然科学版), 2004, 44(2):224-227.(Li Jun-feng, Meng Xin, Gao Yun-feng.J2Perturbation Effect on Relative Orbital Configuration of Satellites in Formation Flying[J].Journal of Tsinghua University(Sci&Tech), 2004, 44(2):224-227.)

[12] 张育林, 曾国强, 王兆魁,等.分布式卫星系统理论及应用[M].北京: 科学出版社, 2008:24-53.

[13] 王兆魁.分布式卫星动力学建模与控制研究[D].长沙: 国防科学技术大学, 2006.

[14] 蒋方华, 李俊峰, 宝音贺西.高精度卫星轨道摄动模型[C].中国第十三届空间及运动体控制技术学术年会, 宜昌, 2008年7月19-23日.

[15] 刘培玲, 周军, 刘莹莹.基于J2项和大气阻力摄动的卫星编队保持方法研究[J].宇航学报, 2010, 31(5):1357-1361.(Liu Pei-ling, Zhou Jun, Liu Ying-ying.The Control Method for Satellites Formation-Keeping Based onJ2Term Perturbation and Atmosphere Drag[J].Journal of Astronautics, 2010, 31(5):1357-1361.)