磁强计辅助基于MEMS惯性器件SINS的初始对准方法研究

高 勇 曹娟娟 唐海红 白焕旭

1．海军驻航天科技集团公司第一研究院军事代表室，北京 100076 2.空间物理重点实验室， 北京 100076 3.北京航天自动控制研究所，北京 100854 4.北京航天发射技术研究所， 北京 100076

随着微机电系统(Micro Electromechanical System，MEMS)[1-2]的迅速发展，出现了基于MEMS技术的微机械惯性器件，惯性器件的微小型化为惯性导航系统的集成化和微小型化奠定了基础。基于MEMS的捷联惯性导航系统(Strapdown Inertial Navigation System based on Micro Electromechanical System，MEMS-SINS)由于具有体积小、重量轻、功耗低、成本低、动态范围宽、响应速度快且便于大批量生产等一系列传统惯导系统无法比拟的优点，日益受到重视，不仅在军事领域，在民用领域也具有广阔的应用前景，是当今惯性技术发展的一个重要方向。

惯性导航系统开始工作时需要确定初始的位置和速度，同时还必须建立起惯性导航系统的初始空间坐标基准，即惯性导航系统的初始对准。对于捷联惯性导航系统，初始对准就是确定其初始姿态矩阵，传统的捷联惯性导航系统初始对准方法是利用陀螺仪和加速度计来进行自对准。但是由于目前国内MEMS惯性器件精度很差，一般MEMS陀螺仪精度都在每小时几十度到上百度左右，不能敏感地球自转角速度，故无法利用硅微陀螺仪进行方位自对准。MEMS加速度计精度一般优于1mg，故利用MEMS加速度计进行水平姿态自对准还是可行的。因此，MEMS-SINS需要利用其他外部传感器辅助才能完成精度较高的方位对准。

本文针对MEMS-SINS无法完成自对准的问题设计了一种利用磁强计辅助MIMU的初始对准方法，并对方法进行了误差分析与仿真验证。

1 磁强计辅助MEMS-SINS初始对准方法

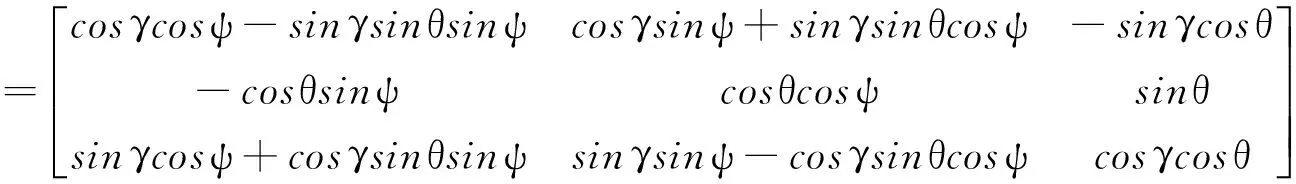
(1)

式中，ψ为航向角，θ为俯仰角，γ为滚转角。

由于方向余弦矩阵为正交矩阵，所以

(2)

MIMU中三轴硅微加速度计的各敏感轴沿载体坐标系各轴向安装，静基座初始对准时，其输出与东北天导航坐标系中比力的关系为：

(3)

由式(2)和(3)只能计算得到2个水平姿态角，不能得到方位姿态角。所以，如果要得到方位角还需要其他传感器辅助。

三轴磁强计[4-5]的各敏感轴沿载体坐标系各轴向安装，利用三个载体坐标系上的磁场强度分量可以确定导航坐标系与载体坐标系的关系[6]：

(4)

(5)

由式(2)和(4)很难计算得到三轴姿态信息，因为任一时刻的测量都只包含两轴信息[7]，不能通过单个时刻测量得到三轴姿态[8]。如果已知2个水平姿态信息，在利用式(4)就能够得到航向角，从而得到SINS初始的姿态矩阵。

所以本文采用三轴硅微加速度计和三轴磁强计的输出综合得到三轴姿态，有3种方法可以选择，具体如下：

硅微加速度计精度较好一些，一般精度优于1mg，故利用硅微加速度计输出进行水平姿态自对准是可行的，能够满足微小型飞行器的姿态要求。

θ=arcsin(fy/g)

(6)

γ=arcsin(-fx/g/cosθ)

(7)

由式(6)和(7)计算得到2个水平姿态角并由此计算得到由载体坐标系到地平坐标系的姿态矩阵如下：

(8)

由于

(9)

(10)

(11)

又因为

(12)

由式(11)和(10)，可得到：

(13)

(14)

利用上式可以得到

(15)

(16)

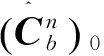
(17)

利用上式可以得到，

(18)

2 误差分析

由于MEMS加速度计和磁强计测量误差，所以分析各种初始对准方法的误差特性对于选择更好的MIMU初始对准方案有着实用意义。

(19)

1)方法1的误差特性

由于2个水平姿态是直接由加速度计输出值直接计算得到，故2个水平失准角为：

(20)

(21)

(22)

2)方法2的误差特性

方法2由下式计算得到姿态阵：

(23)

由于MEMS加速度计和磁强计测量存在误差，则：

(24)

所以：

(25)

令

(26)

(27)

则：

(28)

又因为

(29)

其中

(30)

式中，φE，φN和φU分别为东向、北向和天向的失准角。

由式(19),(28)和(29)可得到

(31)

所以：

(32)

令

(33)

(34)

(35)

所以

(36)

将式(26)和(36)代入式(32)，计算得到：

(37)

由式(30)可得到

(38)

(39)

(40)

3)方法3的误差特性

方法3由下式计算得到姿态阵：

(41)

由于MEMS加速度计和磁强计测量存在误差，则：

(42)

令

(43)

式中：

(44)

(45)

所以：

(46)

将式(44)和(45)代入式(46)，计算得到：

(47)

由式(30)可得到

(48)

(49)

(50)

由式(20)、(38)和(48)可以看出，方法1和方法3在计算东向失准角时的精度相同，都只与北向加速度计偏置有关。但是采用方法2得到的东向失准角精度较差，其不仅与北向加速度计偏置有关，还与天向加速度计偏置和磁强计天向磁场强度误差有关。根据方法2和方法3的误差分析，方法2误差的来源来自式(27)，而方法3误差的来源来自式(45)。由式(27)和(45)可以看出方法2误差量要比方法3大。

由式(21),(39)和(49)可以看出，3种方法计算得到的北向失准角的精度相同。由式(22),(40)和(50)可以看出，3种方法计算得到的天向失准角的精度也相同。

3 计算机仿真

为了验证算法的效果，对3种计算方法进行了仿真，仿真条件为：陀螺仪零偏稳定性约为80(°)/h(1σ)，加速度计偏置稳定性约为1mg(1σ)，磁强计磁场强度测量误差约为80nT(1σ)。

采用这3种方法进行初始姿态角计算，得到的结果如表1所示。表1给出了3种方法计算得到横滚角、俯仰角和航向角解算结果比较。

表1 3种方法解算结果比较表

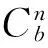
4 结论

本文首先针对MEMS-SINS无法完成初始自对准的问题，设出了一种利用磁强计辅助MEMS-SINS的初始对准方法，并且提出了3种不同的磁强计辅助初始对准的方案，并对这3种方案进行了误差分析，表明第1种和第3种方案精度高，通过仿真证实了理论分析的正确性。

参 考 文 献

[1] Duwel A, Barbour N. MEMS Development at Draper Laboratory[C]//Draper Laboratory-technology Digest 2004: 4-14.

[2] Judy J W. Microelectromechanical Systems (MEMS): Fabrication Design and Applications[J]. Smart Materials and Structures, 2001, 10: 1115-1134.

[3] 万德钧, 房建成.惯性导航初始对准[M].南京：东南大学出版社, 1998.

[4] Lee K M, Kim Y H, Yun J M, et al. Magnetic-interference-free Dual-electric Compass[J]. Sensors and Actuators A, 2005, 120: 441-450.

[5] Ripka P, Vopálenskya M, Platila A, et al. AMR Magnetometer[J].Journal of Magnetism and Magnetic Materials, 2003, 254: 639-641.

[6] Ripka P, Janosek M. Advances in Magnetic Sensors[C]//IEEE Sensors 2008 Conference. IEEE 2008: 1-4.

[7] Yun X, Bachmann E R, McGhee R B. A Simplified Quaternion-Based Algorithm for Orientation Estimation From Earth Gravity and Magnetic Field Measurements[J].IEEE Transactions on Instrumentation and Measurement, 2008, 57(3): 638-650.

[8] 苏琨.纳型卫星星载MIMU模块的研究[D].北京: 清华大学, 2004.