基于混合遗传算法的多冲量最优变轨

付 磊 安效民 覃曌华 徐 敏

西北工业大学航天学院，西安 710072

在航天器变轨的过程中，往往需要尽量减小燃料消耗，以增加航天器有效载荷，或尽量减小变轨时间，以实现快速打击或救援[1]。冲量变轨作为航天器的重要变轨方式具有广泛的研究意义。

近年来，以遗传算法为代表的智能优化算法在非线性冲量最优变轨的研究中得到了广泛应用。Kim和Spencer[2]利用全局搜索能力较强的遗传算法求解两航天器的燃料最优交会问题，并以霍曼转移、双椭圆转移和双冲量交会为例进行了有效性验证。Luo等[3]将混合遗传算法和模拟退火算法应用于冲量交会调相特殊点变轨策略优化设计。周军等[4]采用非线性规划算法研究了在J2影响下，固定时间两异面椭圆轨道间的燃料最省多冲量交会问题。张洪波等[5]利用混合遗传算法对基于轨道要素的共面圆轨道远程交会进行了轨道设计优化和仿真分析。

本文针对燃料和时间指标，基于一种混合遗传算法研究了航天器的交会和拦截问题。仿真结果证明了所建立模型的有效性，并且提出的算法结合了遗传算法和序列二次规划算法的优点，具有较强的全局和局部搜索能力，同时算法的计算速度和精度得到了明显的提高。

1 多冲量最优变轨模型

基于二体动力学模型，以固定时间燃料最优交会问题为例，建立问题的数值优化模型。

交会初始条件为t0,r0,v0，终端条件为tf,rf,vf。为了确定燃料最优解，需要求解一个在时间区间[t0,tf]的最优控制问题，并满足轨道运动方程和指定的约束条件。

冲量施加时，有如下表达式

(1)

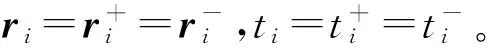
这里假设r(t+Δt)=f(r(t),v(t),t,t+Δt)，v(t+Δt)=g(r(t),v(t),t,t+Δt)为航天器二体运动方程的解。

对于1个中间冲量i≠1,i≠n,n≥2，需要满足条件如下

(2)

第一冲量作用前，对应的初始条件满足

(3)

终端约束如下

(4)

同时满足变轨时刻约束

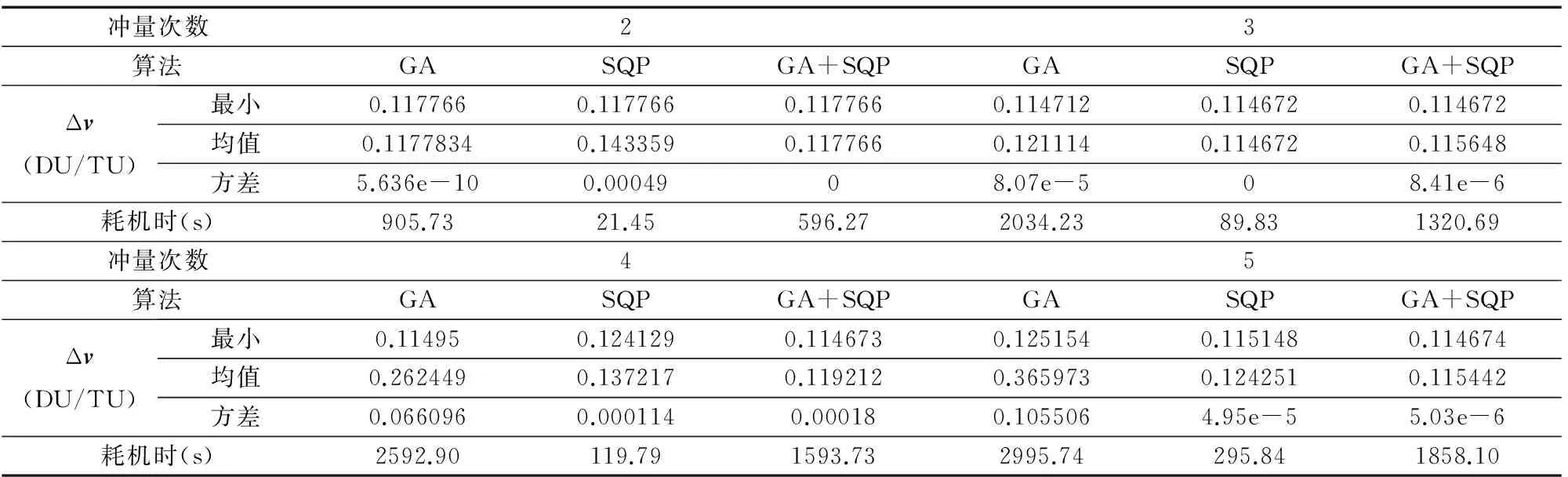
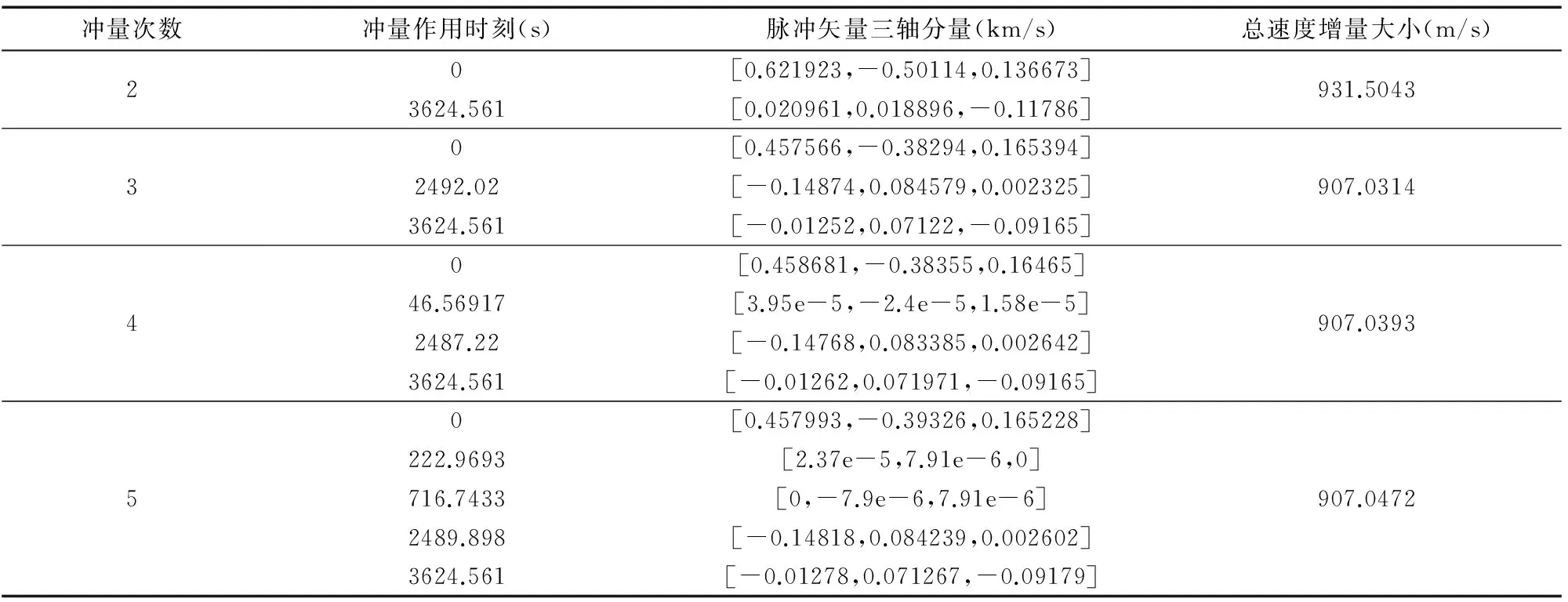
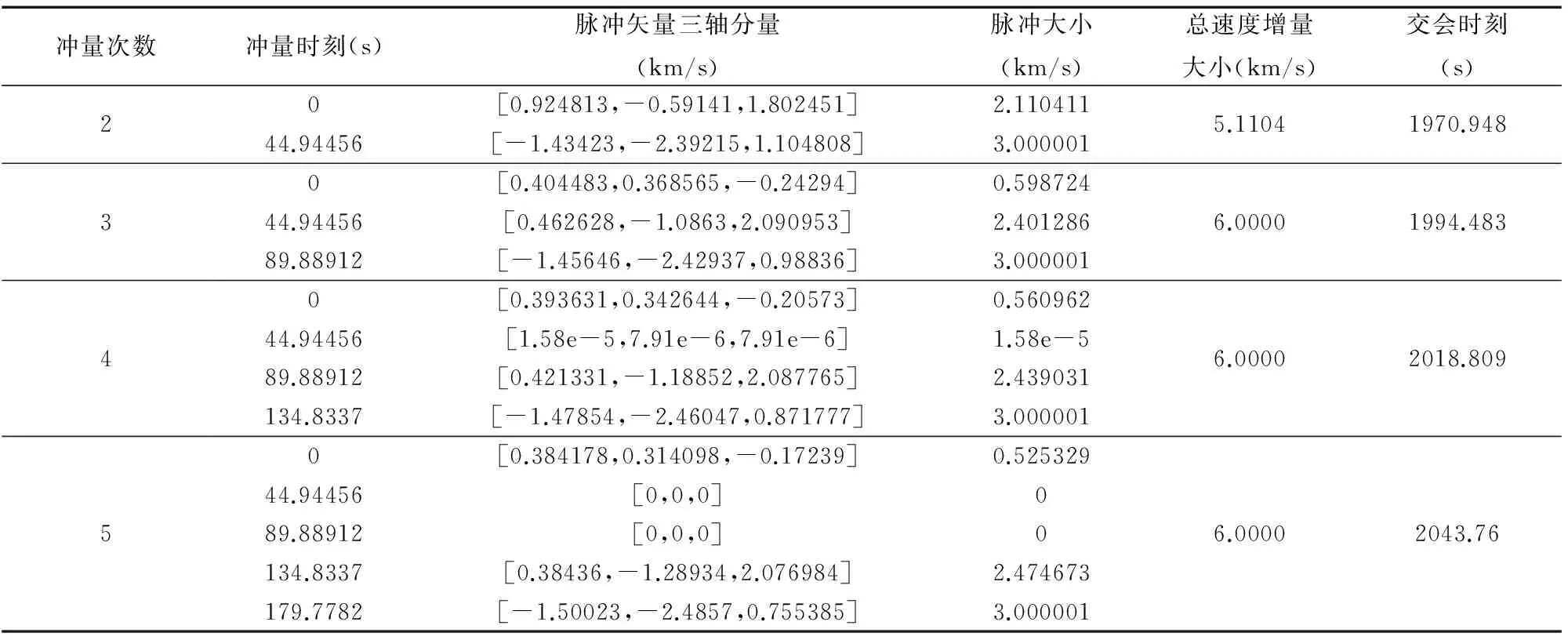
t0≤t1

(5)

以及路径约束

Cl≤C[r(t),v(t),t,p]≤Cu

(6)

和冲量时间间隔约束

ti+1-ti≥tinterval(i=1,…,n-1)

(7)

其中tinterval为冲量施加最小时间间隔。

性能指标函数为

(8)

所以上述多冲量固定时间燃料最省交会可转化为非线性规划问题。为了更好的处理终端约束，引入Lambert算法用于终端条件的自动满足，使得迭代过程中所产生的每一个解均为可行解。此处选择优化变量为

X=(t1,…,tn,Δv1,…,Δvn-2)T

(9)

最短时间拦截的模型与上述类似，主要不同之处在于：拦截问题中追踪航天器的终端速度不受约束；优化变量为X=(t1,…,tn,tf,Δv1,…,Δvn-1)T，性能指标为J=tf-t0。

2 混合遗传算法

GA采用随机搜索原理，包括选择、交叉、变异等操作寻优，具有较强的全局搜索能力和鲁棒性，但其局部搜索能力较弱，结果具有一定的随机性。SQP算法是轨迹优化中应用较为广泛的一种约束非线性优化算法，其收敛速度快，可靠性高，国内外许多大型优化软件都是基于该算法编写的。但该算法需要一个较好的初始点。本文将两者相结合，首先利用GA的全局搜索能力进行初始优化，将优化结果提供给SQP法作为初始点，这种串行优化策略结合了GA和SQP的优点，具有较强的全局和局部搜索能力，同时算法的计算速度和精度得到了明显的提高。算法流程如图1。

图1 混合遗传算法计算流程图

文中遗传算法(GA)编码方式采用实数编码，分别选择随机均匀选择算子、算术交叉算子、自适应变异算子进行选择、交叉、变异等操作，并在选择中采用了最优保存策略，以提高算法的运行效率和收敛速度。GA种群规模为50，交叉概率为0.8。单独GA的最大进化代数为50，GA+SQP算法的遗传最大进化代数为30。

3 仿真算例

首先对数据进行无量纲化操作，令DU为无量纲的距离单位，1DU=6371.004km，TU为无量纲的时间单位，1TU=805.4581s，因此，对应的无量纲速度单位为1DU/TU=7909.7895m/s，此时对应的地球引力常数μ为1。

追踪器初始轨道要素Ec0=(6871km,0.001,97.375°,60°,20°,280°)，目标点轨道要素Ec0=(7171km,0.01,100°,55°,30°,140°)。转移时间满足t∈[t0,tf]，其中，t0=0s，tf=4.5TU=4.5*805.4581s。最小冲量时间间隔tinterval=0.0124*4.5TU。

采用GA，SQP，GA+SQP算法进行仿真。仿真所用计算机的配置为Inter Pentium D CPU 3.00GHz 2.99GHz，3.25G内存。

3.1 固定时间燃料最优交会

对于不同的冲量次数，分别采用GA，SQP和GA+SQP算法进行优化仿真。考虑到算法的随机性，对于给定的冲量次数，每个算法独立运行10次，每次的初始点均由计算机随机产生，统计结果由表1给出。针对不同的冲量次数，表2给出了GA+SQP算法获得的多冲量燃料最优交会的最优解。

分析表1可知，SQP算法的计算速度最快，GA+SQP算法次之，GA算法效率最低；但是通过比较10次计算的均值可以发现，SQP算法除了3次脉冲的情况外，其他情况10次计算的均值与最优值有不小的差距，而GA+SQP算法的均值几乎与最优值相同，说明SQP算法随机性强，全局搜索能力较弱，获得全局最小值的概率较小，GA+SQP算法10次计算得到的结果与最优解均很接近，相对于SQP算法具有更强的全局搜索能力；通过表中的方差一项也可以看出SQP算法的随机性高，不如GA+SQP算法稳定；由于GA算法采用随机搜索方法，该算法具有较强的全局搜索能力，获得全局最优值的概率较大，多次计算获得的最小值可能达到全局最小。GA+SQP算法的串行优化策略结合了GA算法和SQP算法的优点，同时具有了较强的全局和局部搜索能力，提高了算法的计算速度和精度，其优化的综合性能最高。分析仿真结果可知，对于本算例而言，最优的多冲量燃料最优变轨不存在初始和末端自由飞行。为了实现燃料最优交会，交会时间达到最大，这也说明了燃料和时间是2个完全矛盾的指标。多冲量比两冲量更节省燃料。考虑到数值计算的误差，可以认为3、4、5冲量交会消耗的总速度增量大小相等。可见对于多冲量变轨而言，增加冲量次数并不能显著的降低燃料消耗，其意义在于能以较小的单次冲量，实现最终的变轨任务。

另外，由仿真过程可知，对冲量变轨时刻归一化处理能有效提高算法的优化性能和收敛速度。

3.2 最短时间拦截

仿真中最小冲量时间间隔tinterval=0.0124*4.5TU=44.944562s。最短时间拦截的仿真结果如下，图2为用混合遗传算法得到的3次冲量最优变轨的位置矢量和速度矢量时间历程。表3给出了混合遗传算法计算出的最优解。

对于不同的变轨次数，由于优化指标为转移时间最短，故变轨消耗的总速度增量大小均达到允许的最大值，但两冲量变轨除外，这是由于单次冲量大小有限，故冲量次数较少时，将会对变轨能力产生较大的限制。多冲量变轨的最后一次速度增量亦为允许的单次冲量最大值，表明了对于变轨能力受限的情况而言，时间最短拦截要求变轨能力达到飞行器所能提供的能力上限。注意到冲量时刻的间隔均为最小间隔，说明优化过程使每次冲量施加的时刻尽量的靠近，从4次冲量变轨和5次冲量变轨的优化结果来看，出现了零冲量的情况，说明4次冲量和5次冲量的最优结果不如3次冲量变轨的结果。结果表明，冲量次数的增加会增加拦截时间。

表1 多冲量燃料最优交会优化统计结果

表2 混合遗传算法获得的多冲量燃料最优交会优化解

表3 混合遗传算法获得的多冲量时间最短拦截优化解

4 结论

研究了航天器远程导引多冲量变轨问题。建立了基于数值解法的多冲量变轨模型，对燃料最优交会问题和最短时间拦截问题进行了仿真，针对不同的冲量次数，对比了GA，SQP及混合遗传算法的性能，得到了相应的最优冲量施加时刻和大小。从优化的过程来看，混合遗传算法的综合性能最高。分析最优变轨结果得知：对于燃料最优交会问题，3次冲量变轨相比于2次冲量变轨能够显著地减小燃料消耗，但是继续增加冲量次数没有效果。对于最短时间拦截问题，要求变轨能力达到飞行器所能提供的能力上限，并且增加冲量次数会增加拦截时间。

参 考 文 献

[1] 王石, 祝开建, 戴金海, 等.用进化算法求解轨道转移的时间-能量优化问题[J].宇航学报, 2002, 23(1): 73-75.(Wang Shi, Zhu Kai-jian, Dai Jin-hai, et al.Solving Orbital Transformation Problems Based on EA[J].Journal of Astronautics, 2002, 23(1): 73-75.)

[2] Kim Y H, Spencer D B.Optimal Spacecraft Rendezvous Using Genetic Algorithms [J].Journal of Spacecraft and Rockets, 2002, 39(6): 859-865.

[3] Luo Yazhong, Li Haiyang,Tang Guojin.Hybrid Approach to Optimize a Rendezvous Phasing Strategy [J].Journal of Guidance, Control and Dynamics, 2007, 30(2):185-191.

[4] 周军, 常燕.考虑地球扁率J2摄动影响的异面椭圆轨道多冲量最优交会[J].宇航学报, 2008, 29(2): 472-475.(Zhou Jun, Chang Yan.Optimal Multiple-impulse Rendezvous between Non-coplanar Elliptic Orbits Considering the J2 Perturbation Effects [J].Journal of Astronautics, 2008, 29(2): 472-475.)

[5] 张洪波, 郑伟, 汤国建.混合遗传算法在远程交会轨道设计中的应用[J].航天控制, 2006, 24(2): 34-37.(Zhang Hongbo,Zheng Wei, Tang Guojian.The Application of Hybrid Genetic Algorithms in Orbit Design for Long-range Rendezvous[J].Aerospace Control, 2006, 24(2): 34-37.)