一种惯组外场标定振动干扰的分离方法
张 斌 刘洁瑜 李 成
第二炮兵工程大学,西安 710025
惯组标定技术根据场所的不同可分为室内标定和外场标定[1]。外场标定由于没有隔离措施,惯组在进行标定时,人员走动、机器运转造成的地面振动会耦合到惯组的输入中,造成输出信号的抖动,进而影响惯组的标定精度。
目前,对振动干扰的常规处理方法是将该类信号视为野值,采用野值判别准则[2-3]进行处理。然而,该类方法只适用于标定数据中含有少量孤立野值的室内标定法。在外场条件下,剔除野值的方法有一定的局限性,首先,振动干扰不是一个点,而是一段连续的信号;其次,振动干扰是时变的,噪声水平难以估计。文献[4]通过数学仿真表明利用小波模极大值法可以识别惯组输出中的振动干扰,但是该方法缺乏自适应性,需要选择合适的小波函数消失矩阶数和抑制噪声干扰的阈值,也未对如何分离振动干扰作进一步研究。
经验模态分解[5-8](Empirical Mode Decomposition,EMD)是以时变幅度与时变频率信号的瞬时频率为理论基础,不依赖基函数,是数据驱动的自适应分析方法,特别适合非平稳与非线性信号的分析与处理,能清晰地分辨出交叠复杂数据的本征模态。鉴于以上考虑,本文提出一种基于经验模态分解和数字信号滤波技术的振动干扰分离算法。
1 EMD及干扰分离算法
1.1 EMD算法分解流程
经验模态分解方法能把任意非平稳、非线性的信号z(t)分解为若干个本征模态分量(Intrinsic Mode Function, IMF)ci(t)(i=1,2,…,n)和1个残余分量zm(t)。IMF要满足2个条件:1)在整个数据序列中,极值点的数量和过零点的数量必须相等或最多相差1个;2)在任何一点,信号的局部极大值和局部极小值所定义包络线的均值为0。
对于时间信号z(t),其分解步骤如下:
1)计算出信号z(t)所有的局部极值点;
2)采用分段幂函数插值算法求解所有的极大值点构成的上包络线和所有极小值点构成的下包络线,分别记为u1(t)和v1(t);
3)记上、下包络线的均值为:
(1)
并记信号上、下包络线的均值差为:
(2)

5)记z1(t)=z(t)-c1(t)为新的待分析信号,重复步骤1) 至4),以得到第2个IMF,记为c2(t),余项z2(t)=z1(t)-c2(t)。重复上述步骤,直至得到的余项res.是一个单调信号或zm(t)的值小于预先给定的阈值,分解结束。最终得到m个IMF,c1(t),c2(t),…,cm(t),余项为res.,据此,原始信号z(t)可表示为:
(3)
1.2 振动干扰分离算法
(1)时频分析与处理
EMD分解得到的各IMF分量c1(t),c2(t),…,cm(t),其频率是从高到低排列的,通过设计数字滤波器对含振动干扰的前n个ci(t)进行时频滤波分析与处理。由于惯组输出信号的有用信息主要集中在低频范围,而振动干扰一般出现在高频段[9],因此,采用低通滤波器进行数据处理。
(4)
其中,Hlp为低通滤波器。
(2)幅值分析与修正
将EMD分解得到的后(m-n)个IMF分量叠加,得到1个在[t0,t0+T]时间段内振动干扰波形突出的新信号。由于实际数据在大部分时间段内是平稳可靠的,用质量较好的数据来修正非平稳时间段内的数据,即得到消除振动干扰幅值影响的新信号。
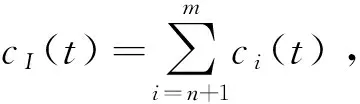
(5)
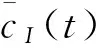
该算法避免了以牺牲大量有用信息为代价的粗糙做法,在保证数据可用的前提下,为得到更多的有用信息,容许部分噪声并存,保持了修正数据与平稳数据时频特性的连续性。
2 振动干扰分离算法的仿真验证
2.1 振动信号的数学模型
外界振动干扰的来源是多方面的,如工作人员的走动、机器的运转、地基本身的运动都可能造成干扰。这类信号通常是由于物体与地基突然撞击引起的,考虑到外场条件下惯组标定的地基通常具有较大的阻尼和较小的弹性系数,振动信号可由下式[10]近似表达:
(6)
式中:E为振动信号的幅度,与地基的弹性系数、阻尼、振源的强度,距离等因素有关;t0为振动峰值处的时间点;Δ为振动信号的时间宽度,决定了振动信号的变化速度,与地基的固有属性有关。
2.2 基于EMD的振动干扰分离
惯组中陀螺仪和加速度计振动干扰分离方法相同,现以加速度计的分离过程为例。在无外界输入和干扰的情况下,惯组中加速度计输出是弱非线性、慢时变的,一般用ARMA模型对其进行逼近,模型如式(7)所示:
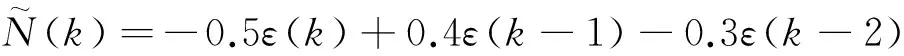
(7)
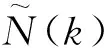

图1 受振动干扰的加速度计输出信号
从图1可以看出在时刻155s处存在一个瞬时振动干扰信号,但在时刻297s处,由于瞬时振动信号与加速度计输出的标准差相同,信号完全被白噪声淹没,利用3σ法显然无法识别出297s处的振动信号。为此,以下采用EMD算法对图1的信号进行处理。
首先,用EMD算法分解该信号,共得到13个imf,如图2所示。由于前4个imf是线性的平稳过程,没有发生频率混叠,因此,不必对其做时频的分析与处理,并且它集中了加速度计输出信号的频率和相位的主要信息,将其保留,即图中的imf1,imf2,imf3和imf4。由图2可知,剩余的imf包含了振动干扰的主要信息,其中res.是信号的趋势项,于是把其余的imf相加得到I:
(8)
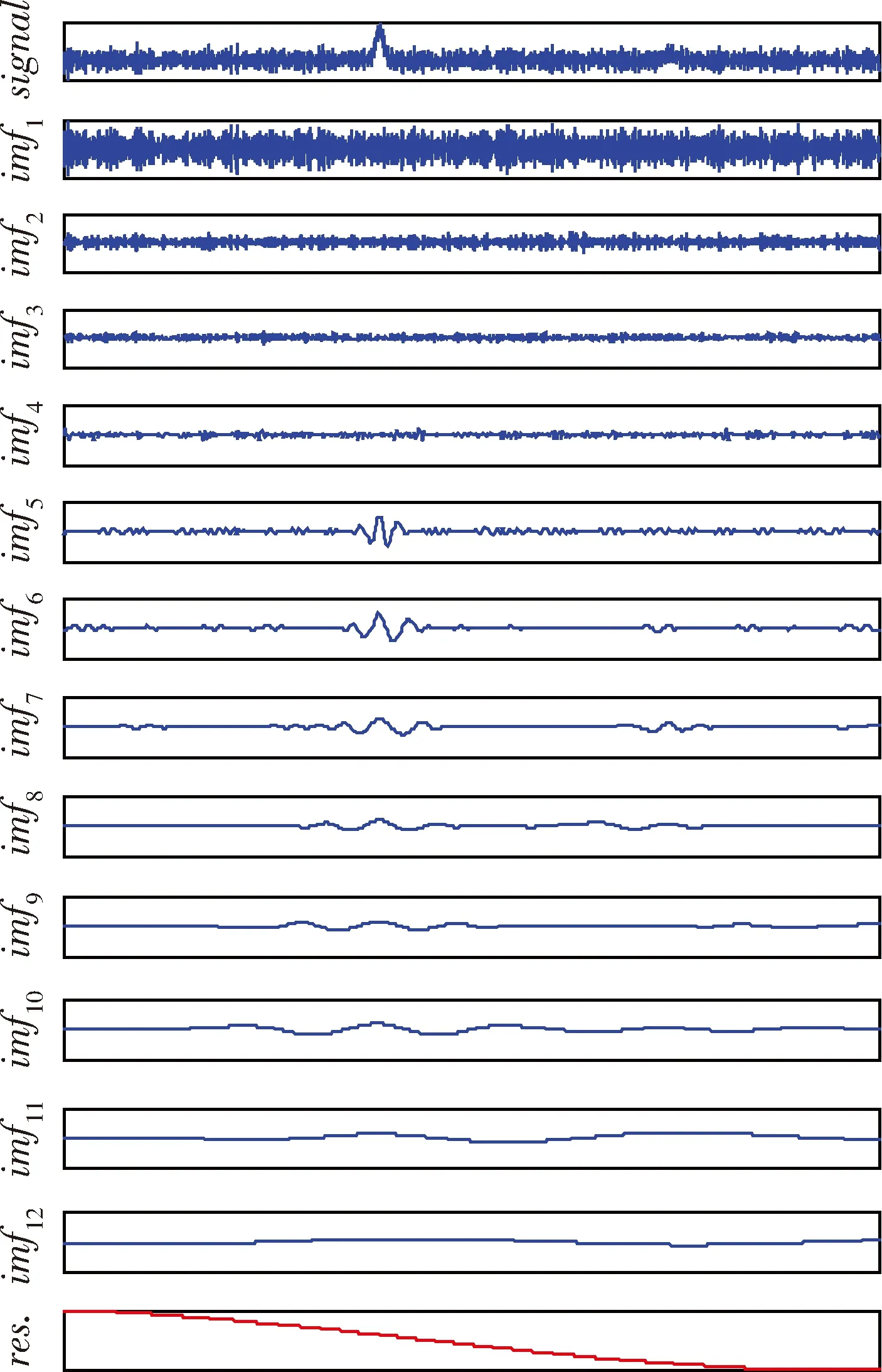
图2 受振动干扰的加速度计输出的EMD分解结果
由图3可知,重构后的信号很好的识别和提取出了干扰信号的波形。根据1.2中幅值修正的方法对该时间段的幅值进行处理,然后将处理后的I与imf1,imf2,imf3和imf4重新叠加,即重构出去除振动干扰后的加速度计输出信号。
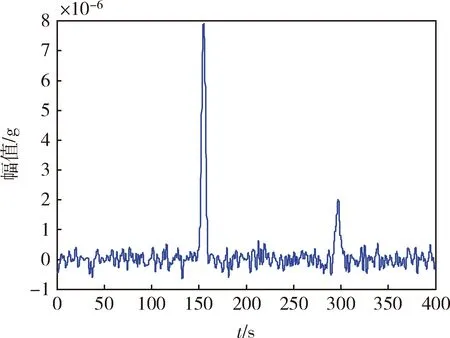
图信号重构结果
通过图4振动干扰信号去除前后偏差率的对比可知,重构后的信号很好的分离了振动干扰。虽然没有复原加振动干扰前的全部真实信号,但是保留了惯组输出的绝大部分有用信息。因此,可以用来代替真实的加速度计输出。
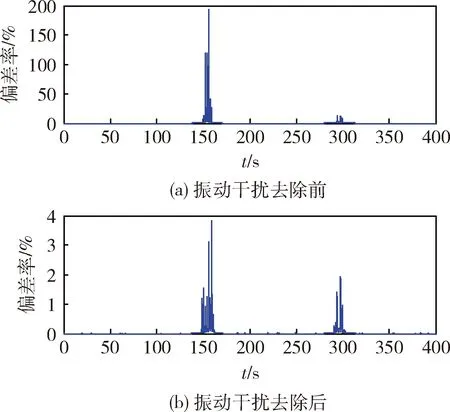
图4 振动干扰信号去除前后的偏差率对比
多次仿真结果表明,该方法可以清晰地分辨出惯组输出中的瞬时振动干扰信号,即使干扰信号幅值小于加速度计输出数据的标准差,该方法仍然有效。
3 应用实例
上面以1个符合ARMA模型的白噪声信号和1个类似脉冲的干扰信号为例来说明振动干扰的分离方法,其情形比较简单。为此,以下采用上述方法对某型激光陀螺惯组中石英挠性加速度计(标度因数为1.26mA/g)实测信号中的振动干扰进行分离。图5为受振动干扰的石英挠性加速度计实测信号,采样时间为20s,采样频率为50Hz。
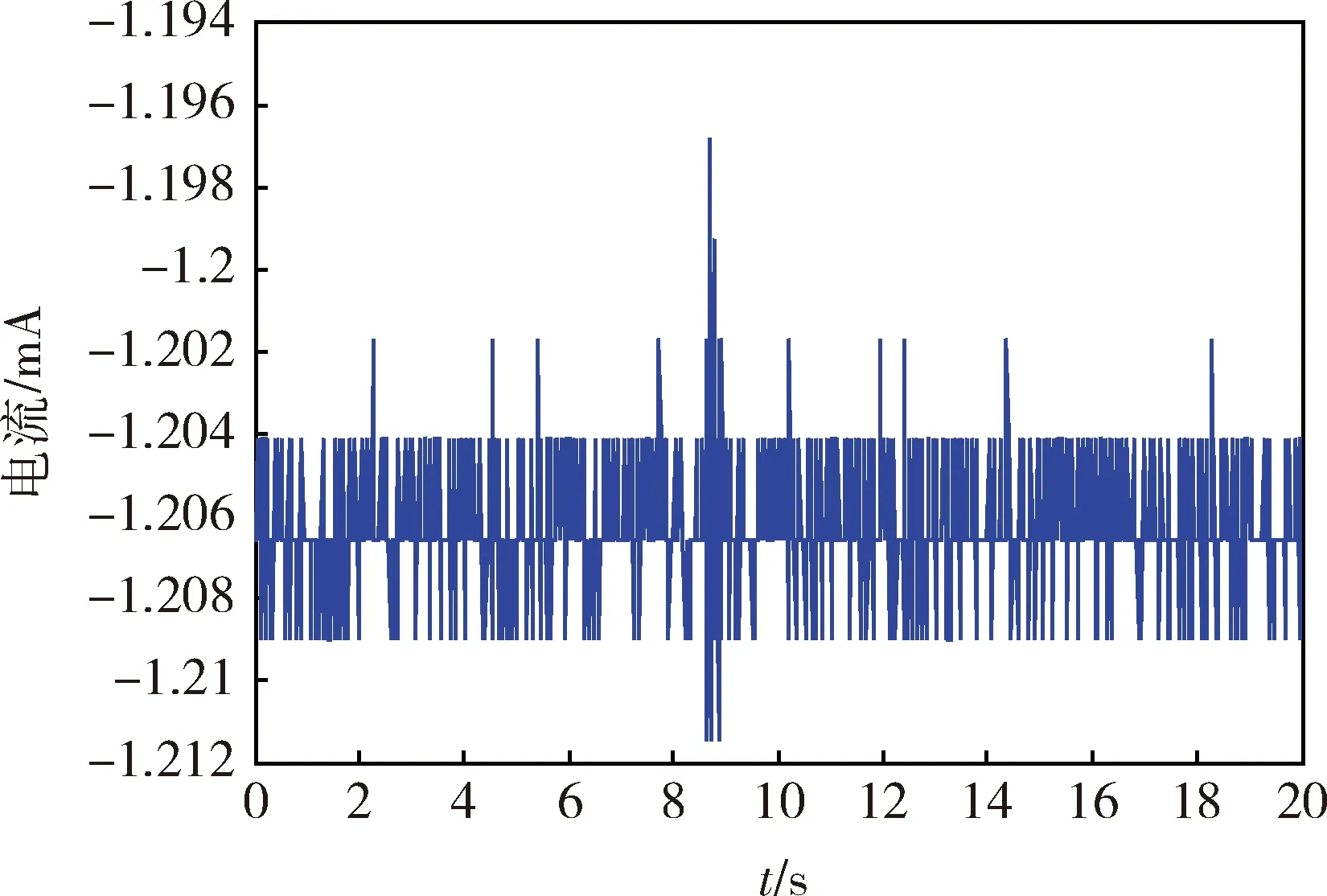
图5 受振动干扰的石英挠性加速度计实测信号
3.1 数据预处理
根据石英挠性加速度计电容位移传感器的测量工作原理,通过激励信号连续对被测电容进行充放电,形成与被测电容成比例的电流或电压信号,从而测量出被测电容值。并且摆片受到振动干扰后,会在平衡位置发生振荡,直至能量衰减为0。因此,如图5所示,石英挠性加速度计实测信号沿Y=-1.206592发生振荡。为便于EMD能清晰地分辨出振动信号,必须对加速度实测信号进行预处理,将时间序列内的数据统一减去-1.206592,并取其绝对值。
3.2 振动干扰分离
对预处理过的数据进行EMD分解,得到10个imf分量,其中振动干扰在imf1中发生了频率混叠。因此,对imf1用功率谱分析的方法来确定低通滤波器的通带范围,并根据实际情况确定滤波器其它参数。图6为imf1经过切比雪夫Ⅱ型滤波器滤波前后的波形对比。
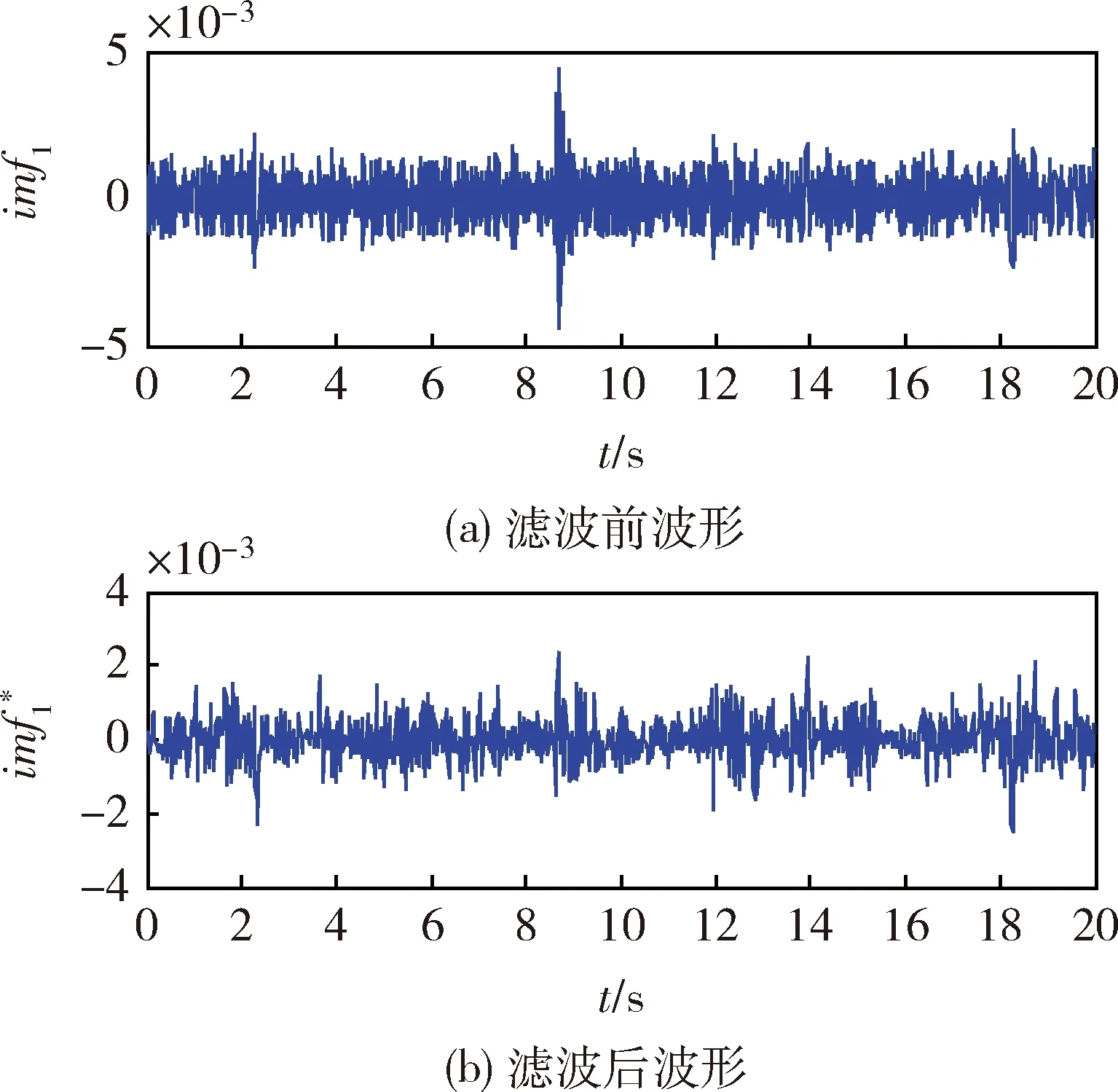
图6 imf1经过切比雪夫Ⅱ型滤波器滤波前后的波形对比
将后7个imf分量叠加得到I0,由图7可以看出,它主要包含了振动干扰的幅值特征,根据1.2节幅值修正算法对该波形进行修正。图7为I0幅值修正前后的波形对比。
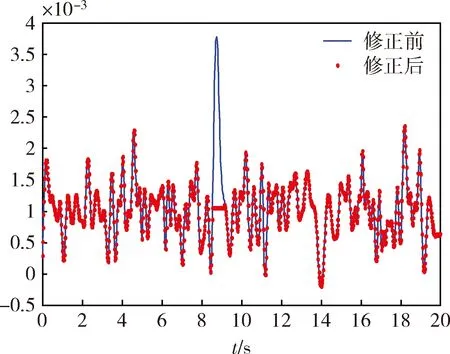
图7 I0幅值修正前后的波形对比
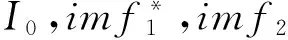
3.3 结果分析
为了能直观地观察重构信号的振动干扰分离效果,对分离振动干扰前后惯组加速度计输出7.5s至10s时间段内的信号进行局部放大,如图8所示。可以看出,基于EMD的滤波法不但较好地剔除了8.5s到9s时间段内的振动干扰,而且保持了原信号的频率特征,这是传统的先用3σ法剔除野值再用滑动平均法平滑处理的方法不能比拟的。由表1可以看出基于EMD的滤波法在整个时间序列内的均值更接近真值,并且方差降低了1个数量级,为2.64234620337422×10-5,而传统方法的方差为4.78241839664939×10-4。

图8 分离振动干扰前后惯组加速度计输出信号局部放大图

无振动干扰的信号基于EMD的滤波法3σ法+平滑处理均值-1.20605414896214-1.20606029528576-1.20624823937560
4 结论
惯组在外场标定时遇到振动干扰,会对惯性仪表输出形成干扰,进而影响惯组的标定精度。因此,剔除干扰、提取有用信息是一项非常重要的工作。传统的数据处理方法,一定程度上删除了数据信号原本有用的信息,没有考虑振动干扰频率分布特性。本文根据惯组输出的特点,提出了一种基于EMD与数字信号滤波技术相结合的分离振动干扰的新方法,该方法克服了传统方法的上述缺陷。通过仿真实验和工程实践,验证了该算法的实用性和数据结果的安全性。
参 考 文 献
[1] 吴文启,张岩,张晓强,潘献飞.激光陀螺捷联惯导系统参数稳定性与外场自标定[J].中国惯性技术学报,2011,19(1):11-15.(WU Wen-qi, ZHANG Yan, ZHANG Xiao-qiang, PAN Xian-fei.Parameter Stability and Outfield Self-calibration of RLG-SINS[J].Journal of Chinese Inertial Technology, 2011,19(1):11-15.)
[2] 费业泰.误差理论与数据处理[M].北京:机械工业出版社, 2010:43-48.
[3] 梅硕基.惯性仪器测试与数据分析[M].西安:西北工业大学出版社, 1991:138-151.
[4] 刘刚,杨杰,汪立新,高江,王晓梅.惯组野外测试时振动干扰的检测与提取[J].噪声与振动控制,2011,4(2):80-83.(LIU Gang, YANG Jie, WANG Li-xin, GAO Jiang ,WANG Xiao-mei.Detecting and Extracting Vibration Disturbing in IMU Outside Calibration[J].Noise and Vibration Control, 2011,4(2):80-83.)
[5] Norden E Huang, Zheng Shen, Steven R Long.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[C].Proceedings of the Royal Society London 1998, 454:903-995.
[6] Flandrin P, Rilling G, Goncalves P.Empirical Mode Decomposition as A Filter Bank [J].IEEE Signal Processing Letters, 2004, 11(1): 112-114.
[7] 丁康,陈健林,苏向荣.平稳和非平稳振动信号的若干处理方法及发展[J].振动工程学报, 2003,16(1):1-10 .(DING Kang, CHEN Jian-lin, SU Xiang-rong.Development in Vibration Signal Analysis and Processing Methods[J].Journal of Vibration Engineering, 2003, 16(1):1-10.)
[8] 王宏禹,邱天爽,陈喆.非平稳随机信号分析与处理[M].北京:国防工业出版社,2008:18-44.(Wang Hong-yu, Qiu Tian-shuang, Chen zhe.Nonstationary Random Signal Analysis and Processing[M].Beijing:National Defense Industry Press, 2008:18-44.)
[9] 曲从善,于鸿,许化龙,谭营.基于经验模态分解的激光陀螺随机信号消噪[J].红外与激光工程, 2009,38(5):859-863.(QU Cong-shan, YU Hong, XU Hua-long, TAN Ying.Random Signal De-noising Based on Empirical Mode Decomposition for Laser Gyro[J].Infrared and Laser Engineering, 2009, 38(5):859-863.)
[10] 杨杰.捷联惯组外场标定动态数据处理与非线性辨识[D].西安:第二炮兵工程大学, 2011.(YANG Jie.Dynamic Data Processing and Nonlinear Identification to SIMU Outside Calibration[D].Xi’an:The Second Artillery Engineering University, 2011.)

