矩阵式AC/DC变换器研究

许柏宏，葛红娟，张文彬，李后春

(南京航空航天大学 自动化学院，江苏 南京 210016)

高频隔离型AC/DC作为一种电力电子装置与电网的接口，对其性能质量的要求已越来越高。这些要求通常包括以下几个方面:近似单位输入功率因数;电源侧电流的谐波失真小;输出电压动态调节;变换器高效、紧凑［1］。基于矩阵变换器的高频隔离型AC/DC变换器即是一种性能优良的交直流变换拓扑结构，也可叫做矩阵式AC/DC变换器，国内外学者对此已有一些研究，并取得了不少成果［2－4］，加拿大学者学者 S Manias［2］最早提出矩阵变换器与高频链的结合，但当时采用的是SPWM调制策略，直流电压利用率比目前常用的SVPWM策略要低15.5%。文献［3］的研究基于双线电压调制策略，重点讨论了开关过程中的占空比丢失等问题，但没有对LC滤波引起的超前无功功率进行分析。文献［4］针对变压器磁复位提出了改进的调制策略，但没有考虑换流过程中的开关损耗。

针对以上缺陷，通过在原边侧串入谐振电感(也可利用变压器漏感作为谐振电感)，并利用开关管的寄生电容，即可将谐振过程引入原边侧换流，实现了双向开关的ZVS开通和ZCS关断，提高了换流的安全可靠性，减少了变换器工作时的开关损耗。系统控制上通过给调制矢量一个滞后分量，来抵消输入侧超前无功功率，实现了单位功率因数控制。

1 基于矩阵变换器的AC/DC变换器

1.1 工作原理

图1为基于矩阵变换器的AC/DC变换器。

图1 基于矩阵变换器的AC/DC变换器

图1 中，Sij(i=P，N;j=A，B，C)为双向开关，三相正弦对称电源uk(k=A，B，C经输入LC滤波后加到变换器输入侧，变换器输出为空间矢量脉宽(SVPWM)调制的高频调制波vPN，经高频变压器与组成全波整流电路后，vPN变换为单向的PWM调制波vrec，最后，经LC输出滤波后，得到所需的直流输出电压U0。

1.2 开关电路调制策略

采用空间矢量调制技术对功率开关进行PWM控制时，由于高频变压器工作时需满足磁平衡以解决双向磁化过程中的磁复位问题，因此在一个开关周期Ts中，变压器初级正负电压面积应当相等，这是该变换器中SVPWM调制所需要满足的特定条件，本文采用如图2所示的优化组合调制方法［4］。

图2 变压器原边侧电压vPN和整流后电压vrec

1.3 直流侧输出电压的表达式推导

Sij(i=P，N;j=A，B，C 开关控制采用电流空间矢量调制技术，输入电流空间矢量调制下占空比计算如下式

给定变换器输入的三相电压

输出直流电压由输入线电压合成，以第一相区为例，单个开关周期中整流侧平均电压如下式

根据式(1)～(3)可得

由上式可知，在输入一定m和Vm时，平均输出直流电压是一定的。再经变压器降压和输出LC滤波后，U0即为恒定的直流电压。

1.4 换流策略

利用高频变压器的漏感和开关管的寄生电容可以在开关过程中引入谐振过程，通过合理地安排双向开关导通和关断的次序，既防止了输入侧短路和漏感能量无法释放的危险，又实现了双向开关的ZVS开通和ZCS关断。

以vPN由正值转换到零区间为例，此时需要把SNB关闭而把SNA打开，则换流过程的时序图如图3所示。具体的换流过程如图4所示，为使图形简洁，只画出了与换流相关的开关。

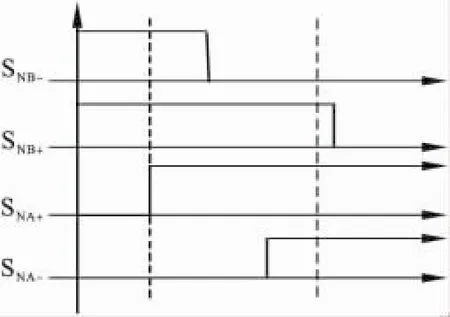
图3 换流过程时序图

图4 Vp由正值转换到零区间的换流过程

第一步:初始状态如图4a所示，开通SNA+，给自身的电容CNA+放电，但是初级电流不会流过SNA+，直到CNA+和CNA－放电完毕才开始导通电流，SNA+实现ZVS开通。

第二步:关断SNB+CNB+从零开始升压，实现SNB+软关断。如图4b所示，初级电流I0/n为等效电容CNB+和CNA－充放电，SNA+开始驱动CNA－的电流。加到初级的电压下降，当结点N的电压达到VAB－VCb，初级线圈的电压变为零，如图4c所示。

第三步:当CNA－放电完毕，DNA－和SNA+开始导通，此时SNA－在ZVS下开通。Ls上的电压为－VCb，初级电流迅速下降。

第四步:SNB－在ZCS下关断，稳态如图4d所示。

软开关换流的应用，使得系统在提高开关频率的同时，开关损耗不会明显增加，电路效率不至于有明显下降，实现了装置小型化、轻量化。

2 闭环控制策略

由于输入滤波器的存在，电源侧电流相比于电源电压会有一定的超前位移。文献［5］提出的控制算法是通过检测电源侧电压与电流的相角差，将此差值经过PI调节控制调制函数延迟角α以实现功率补偿，同时将直流侧参考电压与实际电压的差值通过另一个PI调节器控制调制比m，以达到控制直流侧电压的目的。这种方法具有原理直观、实现方便等优点，但系统的动态响应较慢，同时直流侧电压与交流侧功率因数的控制相互耦合。

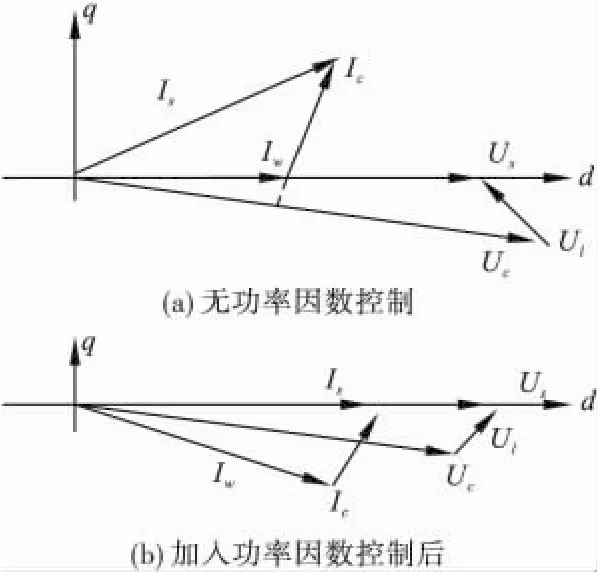
图5 功率因数控制原理图

本文通过给调制矢量一个滞后分量，来抵消输入侧超前无功功率［6］，功率因数控制的原理图如图5所示。旋转坐标系以电源电压作为定向矢量，电源电流的有功分量与无功分量计算式如式(6)。

采用功率因数控制后，式(4)应该修正为

输入侧将计算得到的电源电流无功分量与给定值(设为0)比较，得出调制矢量的q轴分量，输出侧采样电压与整定值比较后经PI调节得到调制矢量的d轴分量md。系统的控制由两个控制环组成，如图6所示，交流侧功率因数的控制与直流侧电压的控制实现了解耦。

当系统本身无法达到单位功率因数时，在首先保证直流侧电压输出调节的基础上，让电源侧输入功率因数达到最大，因此在控制中加入一个饱和处理环节，其中的计算如式(8)。

图6 AC/DC变换器闭环控制框图

3 仿真结果与分析

利用MATLAB/Simulink软件仿真平台搭建仿真模型，模型的输入三相交流电为每相220V/50Hz的对称电源，输出滤波器参数为滤波电感1.2mH、滤波电容20μF，开关频率 10KHz，负载电阻为2Ω，输出电压的整定值为48V。Simulink仿真中高频变压器采用Saturable Transformer模型，变压器原副边匝比为4。

3.1 系统可以达到单位功率因数时的控制

首先对于电源侧可以调节至单位功率因数的情况进行仿真验证，调制矢量的仿真结果如图7所示，直轴分量约为0.42，交轴分量约为 －0.27，即通过滞后交轴分量给电源侧注入滞后电流。图8所示的输入A相电压和电流已基本达到同相位，Simulink/SimPowerSystems中的仿真功率测量模块Active＆Reactive Powe可计算出此时的电源侧功率因数接近1，表明调制分量的交轴分量对超前功率进行了补偿后，成功实现了功率因数调节功能。

图7 单位功率因数下调制矢量的直轴分量md和交轴分量mq

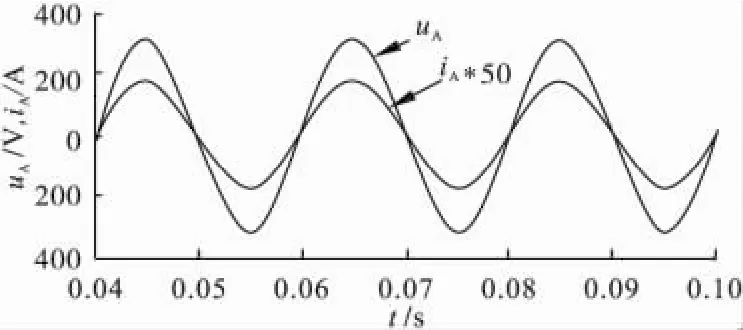
图8 功率因数补偿后网侧A相的相电压与相电流

3.2 系统本身不能达到单位功率因数时的控制

电感取值受体积重量的限制，不易取大。为了取得较好的滤波效果，应提高电容取值，降低截止频率，但电容取值变大时超前无功功率也相应增大，需要调制矢量提供更大的滞后补偿，使得电源侧难以实现单位功率因数。另外，轻载条件下，超前的电容电流对功率因数的影响明显增大。以上两种情况都会使系统本身不能实现输入侧单位功率因数。

为了进一步说明功率因数控制算法在系统本身不能实现单位功率因数时的调节能力，将仿真参数中的输入滤波电容改为50μF，负载电阻为5Ω，输出整定仍为48V。仿真结果如图9所示，调制矢量的直轴分量仍为0.42左右，符合式(7)的计算结果。交轴分量达到式(6)计算的mqmax，表明功率补偿已尽可能最大。如图10所示，此时网侧电流相对于电压存在一个超前的相角，但由前面的分析可知超前的相角已经被调节至最小，功率因数已调节至所能达到的最大值。

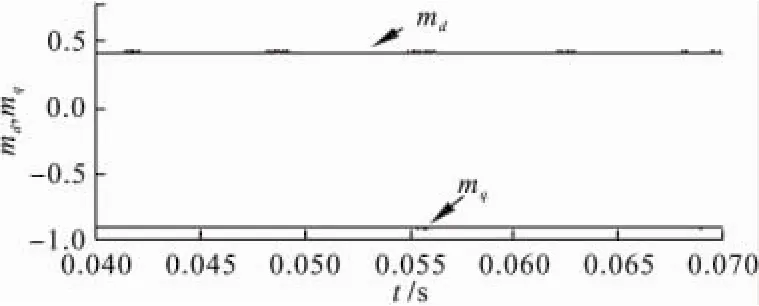
图9 调制矢量的直轴分量md和交轴分量mq

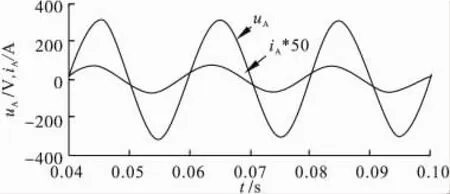
图10 网侧A相的相电压与相电流

3.3 换流过程仿真

利用模拟与混合信号仿真工具Saber可以对换流过程进行仿真分析。仿真主要参数有:谐振电感值为28μH，隔直电容5μF，谐振电容580pF。在原边电压由正区间变为零区间时，图11为开关管导通时的电压与电流波形，基本实现了ZVS开通，图12为开关管关断时的电压与电流波形，由仿真结果可知，关断损耗已降至很低。

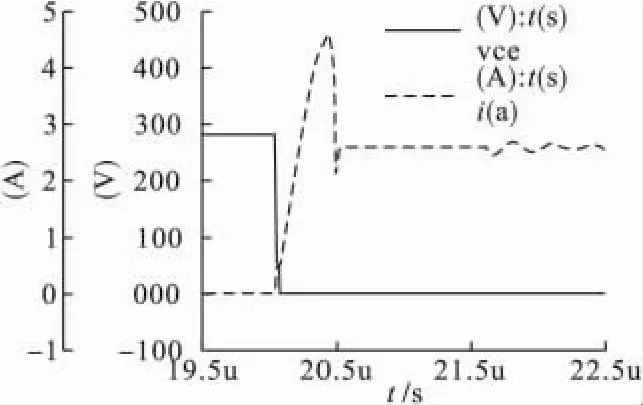
图11 原边电压由正变为零时的开关管开通波形

图12 原边电压由正变为零时的开关管关断波形

4 结论

本文研究了一种基于矩阵变换器的AC/DC变换器，重点分析了系统的调制策略、软开关换流过程和功率因数控制方法。针对系统本身能否达到单位功率因数的两种情况，通过加入饱和处理环节，在系统本身不能实现单位功率因数时尽量提高至最大功率因数。仿真结果与理论分析吻合，验证了分析方法和控制模型的正确性。

［1］Somnida Ratanapanachote，Han Ju Cha，Prasad N.Enjeti.A Digitally Controlled Swit ch Mode Power Supply Based on Matrix Converter［J］.IEEE Trans.On Power Electronics，2006，21(1):124 －130.

［2］Stefanos Manias，Phoivosziogas.A Novel Sinewave in AC to DC Converter with High-Frequency Transformer Isolation［J］.IEEE Trans.On Industrial Electronics，1985，32(4):430 －438.

［3］Vlatko Vlatkovi C，Dugan Borojevi C，Lee Fred C.A zero-voltage switched，three-phase isolated PWM buck rectifier［J］.IEEE Transactions on Power Electronics，1995，10(2):148 －157.

［4］张绍，葛红娟，穆新华.基于AC-AC直接变换的ACDC变换器研究［J］.电力电子技术，2006，40(3):42－44.

［5］Rafael Garcia-Gil，Jose M.Espi，Enrique J.Dede，et al.An All-Digital Controlled AC-DC Matrix Converter with High-Frequency Isolation and Power Factor Correction［J］.IEEE ISIE，2004，2(5):1075 －1080.

［6］谈龙成，李耀华，刘丛伟，等.三相电流型PWM 整流器的功率因数控制方法［J］.电工技术学报，2010，25(2):86－93.