互动过程中师与生的角色定位

洪松

教学过程是教师和学生两种角色共同活动的过程，师生互动必须充分发挥教师的主导作用，体现学生的主体地位。真正的互动应该是建立在师生平等及生生平等的基础之上，只有实现师生认知和地位上的完全平等，才能避免教师的“一言堂”，避免教师或好学生的思维替代，避免师生互动时学生的过分随意，避免生生互动时学生的无序和漫无目的。所以教师在互动过程中要始终发挥其主导作用，不能因为学生主体地位的确立而弱化教师的主导作用，而学生作为认知和发展的主体，只有当他们与教师形成真正的互动，不能因为教师的主导而人云亦云，使教学中的互动丧失其应有的价值。下面我以一道习题的处理谈一谈互动过程中师与生的角色定位。

苏教版义务教育课程标准实验教科书数学六年级下册练习八有这样一道题：

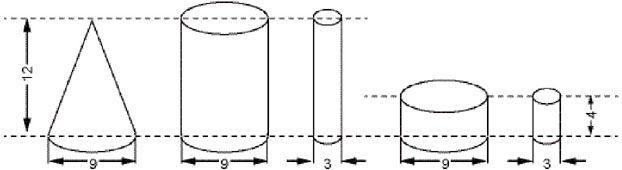
判断下面的圆锥与哪个圆柱白体积相等（见图1）。（单位：cm）

这道题一共有5个立体图形，其中第一个是圆锥，另外四个是圆柱，题目只要求判断圆锥的体积与哪个圆柱的体积相等，需要学生一一加以比对，指向不明确，有一定的难度。为了让学生获得更多的知识和发展，我设计了如下的师生互动的教学过程：

一、师生平等对话，创设民主和谐课堂

（课件出示这一组图形）

师：你能求出其中任意一个立体图形的体积吗？

生：能！

师：举个例子。

生1：圆锥的体积是（9÷2）2×3.14×12×1/3

生2：那个大圆柱的体积是（9÷2）2×3.14×12

师：哪个大圆柱？一共5个立体图形，怎么样就可以让我们一下子就知道你说的是哪一个立体图形？

生2：编号，从左往右按1到5的顺序编号就行了。

生3：也可以用字母ABCDE来表示。

生4：还可以用甲乙丙丁戊来表示。

简析：师生要实现真正的互动，必须要有民主和谐的氛围，几个简单的问题可以帮助学生迅速进入主体角色。另外有效学习是建立在有序思维的基础之上，看似简单的编号却解决了5个立体图形的定位和次序的大问题，这样可以使学生的思维指向性更加明确，表述更加清晰而富有条理，便于师生互动，生生互动。

二、一石激起千层浪，教师要做一枚有价值的引路石

师：你能说说其中任意两个立体图形的体积之间的关系吗？

生5：能，例如①号圆锥的体积是②号圆柱的1/3。

师：为什么？

生5：因为它们等底等高。

生6：因为②号和③号的高相等，而②号的底面直径是③号的3倍，底面积就是它的9倍，所以②号的体积就是③号的9倍。

师：还有吗？

…… （下转第81页）（上接第79页）

（学生举手积极，课堂气氛活跃。我见此情景，顺势引导学生分组讨论整理。接着分组汇报，每组选一个代表把整理的关系写到黑板上，提醒不遗漏，不重复。）

简析：在很多情况下，学生的思维就像一條平静的小河，缓缓的流淌，而此时的互动需要教师主导作用的发挥。老师及时投出的一枚石子，可以激发学生美丽的思维浪花。

师：还有吗？

（学生沉寂了一会儿）

生7：没有了！

师：你怎么知道的？

生7：我看好像全找出来了。

生8：没有了！因为5个立体图形，两两一组一共可以组成10组，黑板已经有了10组。

师：为什么两两一组可以组成10组？

生8：举例说先拿①号出来和其它4个配对，就一共有4组，再拿②号，和余下的配对，又有3组，以此类推，一共就是4+3+2+1=10组。

（掌声已经响起来了）

简析：这一环节是课堂的自然生成，在教师的步步紧逼下，学生的思维在激荡。虽说只是老师与生8一对一的问答互动，但是绝大部分同学在充分思考的前提下，对生8答案的认可和赞赏，充分表现出同学们在思维上的互动。

三、师生、生生和生本全方位的互动，使学习走向深入

师：我们一起来研究这10组关系，这样写在黑板上太乱了，怎么办？

生：分类

师：怎么分？

生9：①号和②③④⑤号的关系为一组，其余为一组。

（他把圆锥与圆柱之间的关系分为一组，圆柱与圆柱之间的关系分为一组。）

生10：等底等高为一组，等底不等高为一组，不等底等高为一组，什么都不等的为一组。

师：哪种分类更有价值呢？你们能够分一分吗？

（我引导学生把10组关系按第二种标准分类。因此黑板上出现了这样的板书：

师：为什么①和④的体积相等呢？

生11：因为①和④的底面积相等，而①是圆锥，求体积时还要乘以，所以①和④的体积相等。

师：为什么①的体积是③的3倍呢？

生12：因为①是③的高相等，而①的底面积是③的9倍，①又是圆锥，求体积时还要乘以，所以①的体积是③的3倍。

师：为什么①的体积是⑤的9倍呢？

生13：因为①的底面积是⑤的9倍，①的高是⑤的3倍，如果①是圆柱，那么它的体积就是⑤的27倍，但①是圆锥，求体积时还要乘以，所以①的体积是⑤的9倍。

……

简析：在这一环节中，有师生互动，例如就任意两个立体图形的体积关系的问答，有生生互动，例如学生对分类标准的争论，有生本互动，例如学生对黑板上素材的归类整理。在全方位、多层次的互动过程中，教师与学生的角色近于模糊，学习走向深入。

【作者单位：淮阴师范学院第一附属小学 江苏】