“小题大做”精选巧练 “借题发挥”提升价值
周利红

摘 要:习题是数学教材的重要组成部分,学生在数学课堂上建立起新概念、习得规律之后,必须完成一定数量的练习题,才能巩固所学知识,正确理解概念、定理、公式等,逐步形成技能、技巧,不断提高观察、比较等思维能力。教师在课堂教学中,要认真钻研数学教材,吃透习题设计的意图,把握习题的实施要求,选取典型适度的习题。让学生在教师精心组织的数学课堂练习中触类旁通、观微知著、自醒自悟,既能达成对知识的深刻理解,又能积累丰富的数学活动经验,并逐步形成数学思想和方法。
关键词:选用;整合;提升;改编
习题是数学教材的重要组成部分,学生在数学课堂上建立起新概念、习得规律之后,必须完成一定数量的练习题,才能巩固所学知识,正确理解概念、定理、公式等,逐步形成技能、技巧,不断提高观察、比较等思维能力。习题教学是课堂教学不可忽视的环节,对发展学生能力、建构学生认知结构、训练学生思维等方面发挥着举足轻重的作用,也是体现教学有效性的重要环节。
《全日制义务教育数学课程标准(实验稿)》指出:基本技能的形成,需要一定量的训练,但要适度,不能依赖机械的重复操作,要注重训练的实效性……根据内容的要求和学生的实际,分层次落实……经历发现数学问题、解决数学问题的过程,在主动参与数学活动的过程中,不断反思,逐步积累数学经验,感悟数学思想。这就要求教师在课堂教学中,认真钻研数学教材,研究其各类练习题的配备,吃透习题设计的意图,把握习题的实施要求。选取典型适度的习题,精心组织,变有限为无限,让学生在教师精心组织的数学课堂练习中触类旁通、观微知著、自醒自悟,既能达成对知识的深刻理解,又能积累丰富的数学活动经验,并逐步形成数学思想和方法。下面笔者根据自身的教学实践及探究,浅谈数学课本习题有效使用的几点策略。
一、有的放矢,灵活选用课本习题
课本习题是数学课堂教学中学生进行练习的重要环节,学生在这个环节中如何实现有效“突破”,占领“目标”,教师的“排兵布阵”至关重要。教师要根据教材内容、教学目标和教学重难点,结合学生的思维特点和认识发展的规律,同时遵循由易到难、由浅入深、由基础到提高的原则,灵活选用课本练习习题,提高习题练习的质量。
例如,笔者在教学五年级《最大公因数》这一课时,在学生基本形成“最大公因数”的概念后,结合课本习题安排了如下练习
环节:
1.尝试:找出18和27的公因数与最大公因数。
怎样才能既不遗漏又按顺序地找到18和27的公因数与最大公因数?
2.找一找。
(1)10和15的公因数有 。
(2)14和49的最大公因数是 。
说一说你是怎样找的?
3.找出下面每组数的最大公因数。
16和32 30和45
4.选一选。
(1)8和20的公因数有( )。
①4 ②2,4 ③1,2,4
(2)一个数是13,另一个数比它大1,这两个数的最大公因数是( )。
①2 ②1 ③7
5.解决问题。
如果把两个班的学生分别分成若干个小组,要使两个班每个小组的人数相同,每组最多有多少人?
以上练习安排,是将书本上的例题和习题进行了有效的整合和灵活处理,这样的习题编排,由浅入深,由易到难,环环紧扣,逐步提高。既有一定数量的基本练习,又有一些变式习题,有利于学生巩固新知,拓展学生思路,有利于学生加强实践应用,促使知识向技能的转化。
二、循序渐进,整合提升课本习题
刘加霞博士指出,从“冰冷的美丽”到“火热的思考”,离不开教师精心的教学设计和充满智慧的组织与控制,否则,不可能实现有效的教学。教师要潜心钻研教材,把握知识结构,充分利用教材的习题资源,对知识点进行有机整合和提升,对习题作出适度而有效的开发,从立体的、多维度的角度把握各部分数学知识之间的关联,注重知识的重组和综合运用,提高教材的“附加值”。
例如,教学五年级上册《平行四边形的面积》这一内容时,在练习环节的设计中,为了使练习的效率和价值更高,把82页练习十五中的1~4题进行了整合提升,改编如下题。
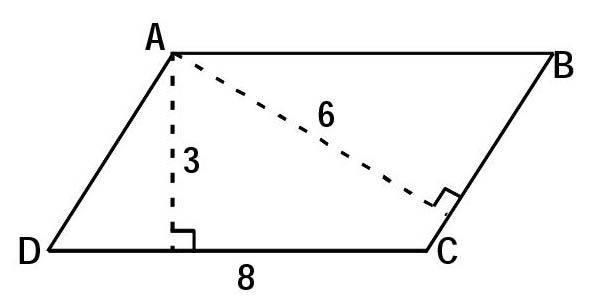
1.练一练:下图是一个平行四边形花坛。(单位:米)
(1)你能求出这个花坛的面积吗?
(2)它的面积是多少平方米?(课件呈现数据)
(3)BC长是多少米?
(4)如果这个花坛的底和高都是整米数,且面积是24平方米,那么底和高分别是多少米?
(5)底和高是怎样变化的,你发现了什么?
(6)当底是24米,高是1米时,这个平行四边形是怎样的?
根据课本4个习题的安排意图和学生的实际,在教学中进行了以上改编整合,题(1)让学生思考计算平行四边形的面积需要哪些数据,同时获得解决问题的一些策略,如要求面积需要先测量哪些数据;题(2)则是让学生在计算面积的过程中体验应该选择怎样的数据,明确只有底和高对应时才能应用公式进行计算。以上2小题是对课本前两题的整合,让学生经历设问、思考、选择、解决的过程,学习活动更为丰富。
题(3)是对课本第3题的应用,当学生计算出这个花坛的面积后,再求BC边的长度,放手让学生解决,在操作、汇报、交流的过程中让学生体会解决问题的方法的多样性,同时学生的思维得到了发展和提升。如:
师:把你们解决的方法和大家交流一下。
生:24÷6=4(米),因为花坛的面积是24平方米,知道了BC边上的高是6,要求这条高对应的底,只要面积除以高就可以啦!
生:我是用方程解决的。把BC边的长度设为x米,列出方程6x=24,再求出x=4就可以啦。
生:我是直接8÷2=4(米)。
师:你的方法很特别,你是怎么想的?
生:这个花坛的面积不会变,刚才的底边上的高是3米,而BC边上的高是6米,是3米的两倍,那BC边的长度就应该是刚才底边的一半,所以直接用8÷2来计算。
生:老师,我发现底和高之间的倍数关系是相反的,一条底边是另一条底边的几倍,而另一条高是这条高的几倍。(一个学生兴奋地指着屏幕发表自己的意见。)
……
生:这和我们以前学过的积的变化规律一样,一个因数扩大几倍,另一个因数就缩小几倍。
……
这样的设计,比起书本中单纯的已知面积和底,让学生逆向求高的习题,知识结构清晰,思维含量丰富。题(4)~(6)的练习学生兴趣盎然,思维积极,其中不但体现了有序思考、数形结合的思想,而且通过想象发展了学生的空间观念。整个练习环节的设计注重层次,循序渐进,通过练习不仅巩固了学生的基础知识和基本技能,更让学生经历解决数学问题的过程,在主动参与数学活动的过程中,不断反思,逐步积累数学经验,感悟数学思想。
三、注重开放,有效改编课本习题
有效的数学学习过程不能单纯地依赖模仿和记忆。课堂练习是使学生熟练掌握知识,培养思维品质的具体措施,因此,练习设计要减少指令性成分,增强练习的开放性,以使学生的思路更广阔、更灵活。练习的开放性是指那些条件不完备、结论不确定的数学问题,学生在开放的问题情境中学会分析、学会探索、学会思考,主动构建数学知识体系,有利于拓宽学生的思维空间,挖掘学生的创造潜力,培养学生的创新意识。
例如,在六年级总复习“空间与图形”中,第100页题5求平面图形的面积,在教学中做出如下的改编:
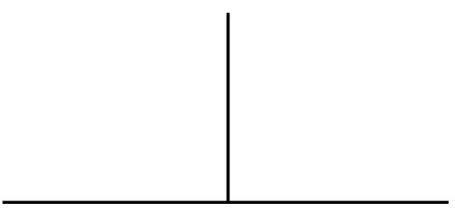
(1)下图中的两条线段是什么关系?(互相垂直)
(2)如果水平线段的长度是垂直线段长度的2倍,根据这幅图你能想象出哪些我们学过的平面图形?(独立思考、动手操作、小组交流)
(3)如果水平线段长4厘米,你能算出这些图形的面积吗?
复习课就是把平时相对独立地进行教学的知识,特别是其中带有规律性的知识,以再现、整理、归纳等办法串起来,进而加深学生对知识的理解、沟通,并使之条理化、系统化。六年级“平面图形的整理与复习”这一课的目的在于学生对所学过的长方形、正方形、三角形、梯形、平行四边形、圆的面积公式做出整理。因此,设计这样的一道练习题,让学生在开放的情境中主动地复习小学数学中平面图形的特征,以长方形为基本的元素主动构建各种平面图形的联系和区别,更关注知识的“生长点”和“延伸点”(各个图形的面积=母线×高),学生通过观察、想象、操作等活动,不但巩固了基本知识和技能,形成了知识网络,而且进一步发展了空间观念和数学思想。
练习是掌握数学知识、形成技能技巧的重要手段,是培养学生能力、发展学生智力的重要途径。有效的练习不但能使学生快速、深刻地巩固知识,熟练技能,同时还发展学生的思维,培养学生的综合能力。习题教学是数学课的重要组成部分,我们一线的数学教师应注重根据教材编排的习题内容,围绕教学目标,精心设计课堂习题,提高练习效率,不能局限于机械操作,而应以其灵活的设计形式和丰富的练习内容,使数学习题的功能得到不断拓展,数学活动的价值得到不断提升。让孩子在触摸数学中,激活自己的灵性,在思考问题中感受思维之美,在探索解决问题中体验学习之乐,真正追求智慧而有效的课堂教学。
参考文献:
[1]曹培英.提高小学数学练习设计有效性的研究.小学数学教师,2011(04).
[2]吴登文.从分数知识的教学看小学数学教师的专业素养.小学教学,2011(05).
[3]宇文森.小学数学:名师高效教学设计艺术.西南师范大学出版社,2010-03.
(作者单位 浙江省余姚市肖东第二小学)

