基于输入输出线性化的航迹滑模控制及仿真

吴瑶，吴汉松，袁雷



基于输入输出线性化的航迹滑模控制及仿真

吴瑶，吴汉松，袁雷

（海军工程大学，武汉 430033）

针对船舶航迹控制系统的非线性及易受外部干扰的特点，提出了一种基于输入输出线性化的航迹滑模控制策略。通过定义输出变量将非线性航迹控制系统转化为线性系统，然后采用指数趋近律的滑模控制方法设计控制器，使得设计的非线性控制律直观简洁，鲁棒性好。通过SIMULINK仿真验证了该算法的有效性。

非线性 船舶航迹控制 输入输出线性化 滑模变结构控制

0 引言

随着人们对海洋资源的开发和利用，作为海上运输工具的船舶向大型化和高速化方向发展，海上交通密度的不断加大，航行安全越来越受到威胁[1]，常规的航向自动舵因不能直接实现航迹偏差的控制，已渐渐不能满足要求。随着全球定位系统（GPS）等先进导航设备在船舶上的应用，人们开始设计精确的航迹自动舵来保证船舶行驶在给定航线上。

目前船舶航迹控制的算法研究取得了一定的成果。文献[2-3]通过应用不同的控制方法设计局部指数镇定的控制律，但前提要求艏摇角速度不为零。文献[4-5]通过定义不同的输出变量，提出了船舶直线航迹控制系统全局渐近稳定的充分条件，将非线性系统线性化设计控制器，克服了艏摇角速度不能为零的局限但在外界干扰的影响下鲁棒性差。文献[6-7]采用反步法和其他算法结合的方法使控制律的设计，抗干扰能力强，但控制器设计过程复杂。

本文通过采用输入输出线性化的方法将航迹控制的非线性数学模型线性化来解决航迹控制中的非线性问题，然后利用滑模控制鲁棒性强的优点设计滑模变结构控制器。并考虑风、浪、流等外界干扰对某实习船进行仿真分析，设计过程简单，鲁棒性好，仿真结果验证了本文控制算法的有效性。

1 船舶航迹控制的数学模型

图1为船舶航迹控制坐标示意图，其中x，y是船舶重心相对于固定坐标系XOY的坐标。

船舶航迹控制的数学模型可用以下非线性状态方程表示[5]：

图1 船舶航迹控制坐标

式中，为船舶横向位移，为航向角，为船舶前进速度，为艏摇角速度，为船舶控制舵角，由船舶的方型系数、吨位、载重及航速等因素决定。

若设定直线航迹与正北方向重合，则艏偏角就等于航向角，航迹控制就转化为控制船舶横向位移及航向角使其为零。

2 控制器的设计

2.1 航迹控制输入输出线性化

1) 定义输出变量全局渐进收敛于零；

从而系统的非线性状态空间方程为:

其中

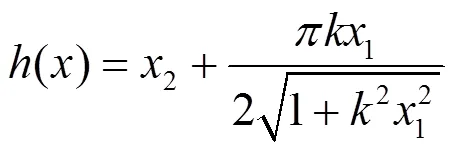
对m求时间导数有

对m求时间导数有

(4)

求以下李导数

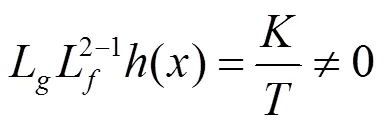
由式(7)知系统相对阶为2，求得状态方程的反馈控制律为：

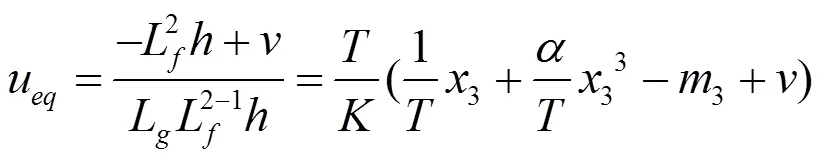
取坐标变换

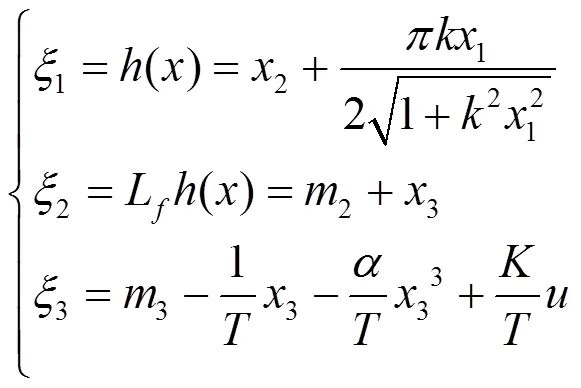
将式(8)代入式(9)得线性化后的系统状态方程：

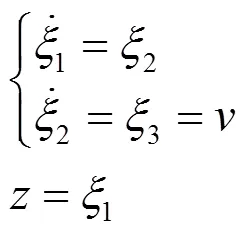
2.2 滑模变结构控制器设计

通过输入输出线性化及微分同胚坐标变换，船舶航迹的非线性数学模型转换为线性状态方程，从而将非线性控制问题转换为线性控制问题，为减小干扰对船舶控制的影响，要求船舶自动舵具有较强的鲁棒性，应用滑模控制对内部参数的变动和外部扰动作用具有的不变性，可以设计强鲁棒性的控制器。

图2为输入输出线性化变结构滑模控制方块图，其中δ为等效舵角干扰。线性化之后系统以为输入，以ξ为输出，ξ为船舶横偏位移的函数，只要ξ渐进收敛则能保证横偏位移收敛。

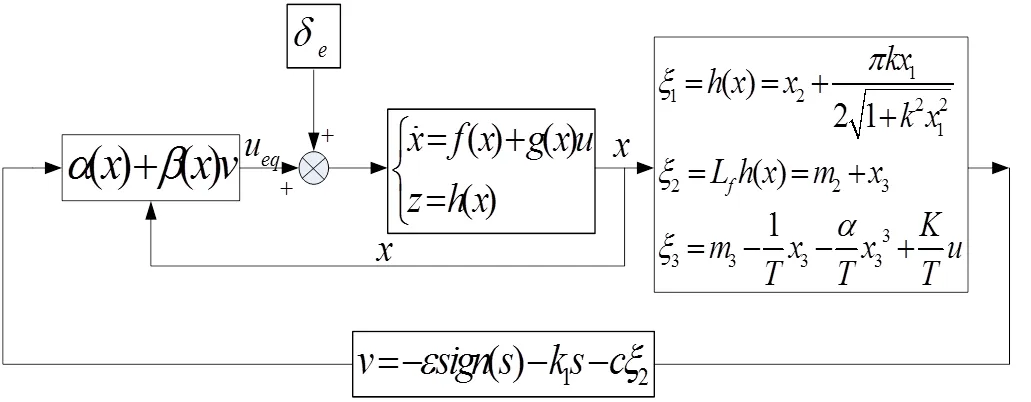
图2 输入输出线性化变结构滑模控制方块图

其滑模变结构控制过程由两部分组成，(1)到达阶段，要保证切换面=0以外的相轨线在有限时间内到达切换面，即系统的可达性。(2)切换面是滑动模态区，且滑动运动渐近稳定，动态品质良好[8]。

2.2.1滑模面设计

经过线性化的航迹控制系统的状态空间方程如式(10)，设期望输出为ξ,定义

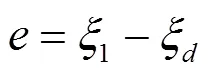
设滑模面为

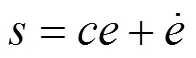
2.2.2设计控制律

能够趋近并到达切换面的条件为

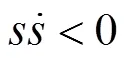
但本条件并不能反映运动是如何趋近切换面的，不能保证趋近过程良好的品质，因此采用趋近律的方法来设计控制。

取指数趋近律：

其中，k为大于零的常数，减小，增大k可使趋近律加快，抖振削弱[9]。

设李亚普诺夫函数：

从而：

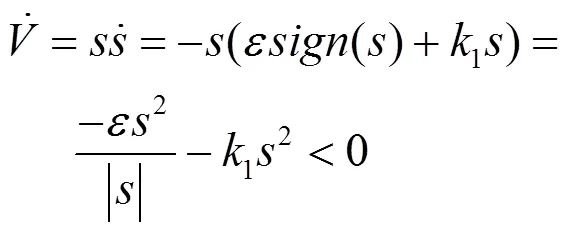
从而证明了整个控制系统在李亚普诺夫意义下渐进稳定。

联立式(12)和(14)得

将式(17)代入(8)可得最终反馈控制律为

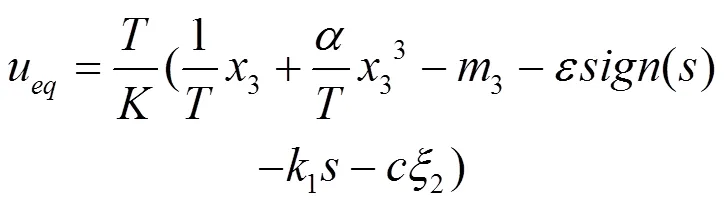
式中和k的值通过仿真调试得出。

3 仿真研究

以文献[10]中实习船为例进行仿真设计。仿真参数如下：船长为126 m，船宽为20.8 m，满载吃水为8.0 m，方型系数为0.681，船速为7.7 m/s.通过计算得= 0.478，=216, 取=30; 采用基于输入输出线性化的滑模控制律式(18)，选取输出变量参数=0.0017，滑模面参数为=0.08;=5*10-7;k=0.02。

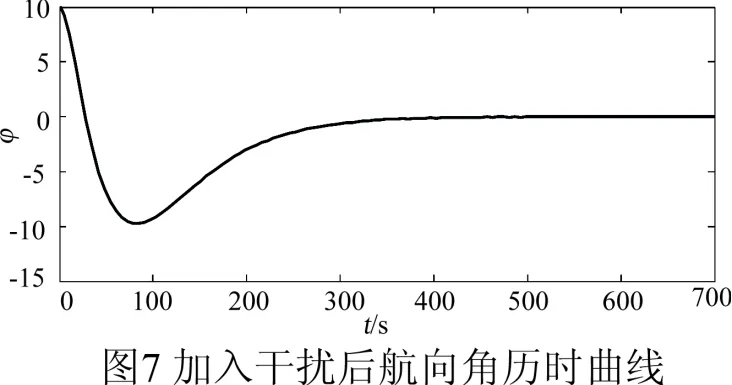
图3-8表明，本文提出的基于输入输出线性化的航迹滑模算法可以使船舶的航迹偏差以指数速度渐进收敛到零点的一个较小临域内，在加入干扰后仍能保持良好的控制效果，体现出了强鲁棒性。

4 结语

针对船舶直线航迹控制的非线性数学模型，本文在文献[5]基础上重新定义输出，将非线性模型线性化，并加入滑模变结构控制，设计的控制器能够克服艏摇角速度不为零的局限，同时对内部参数变动及外部扰动具有较好的鲁棒性，仿真结果表明，设计的控制器可以快速使船舶稳定在设定航迹上，控制输入合理有效，调节参数较少，计算简单，有一定的实用意义，但加入扰动后控制输入抖振明显，有待进一步研究。

[1] 李丽娜．航海自动化[M]．人民交通出版社，2000, （1）:55-76．

[2] Godhhavn J M, Fossen T I, Berge S P. Nonlinear and adaptive back-stepping designs for tracking control of ships[J]. Int. J. Adapt. Control Signal Processing, 1998, 12(8): 649-670.

[3] Pettersen K Y, Nijmeijer H. Under actuated ship tracking control: Theory and Experiments [J]. Int. J. Control, 2001, 74(14): 1435-1446.

[4] 周岗，姚琼荟，陈永冰等. 不完全驱动船舶直线航迹控制稳定性研究[J]. 自动化学报，2007, 33(4): 376-384.

[5] 周岗, 姚琼荟, 陈永冰等.基于输入输出线性化的船舶全局直线航迹控制[J]. 控制理论与应用，2007, 24(1):117-121.

[6] 潘永平，黄道平，孙宗海. 欠驱动船舶航迹Backstepping自适应模糊控制[J]. 控制理论与应用，2011, 28(7):907-914.

[7] 李长喜，冯远静，俞立. 基于Backstepping方法的不完全驱动船舶直线航迹控制的设计[J]. 船舶工程，2008, 30(4):64-66.

[8] 高为炳．变结构控制理论基础[M]．北京：中国科学技术出版社，1996：26-27．

[9] 姚琼荟，黄继起，吴汉松．变结构控制系统[M]．重庆：重庆大学出版社, 1997．

[10] 袁雷，宋立忠．模糊滑模控制在船舶航向非线性系统中的应用[J]．中国航海,2010, 33(1):61-64.

Sliding-mode Controllers for Ship’s Track-keeping Control Systems Based on Input-output Linearization

Wu Yao, Wu Hansong，Yuan Lei

(Naval University of Engineering, Wuhan 430033, Hubei, China)

TP11

A

1003-4862（2013）01-0004-04

2012-05-03

吴瑶（1989-），男，讲师。研究方向：船舶非线性控制。