基于星间星地链路的整网批处理定轨算法仿真研究*
杨遵龙,董绪荣,李晓宇
(装备学院,北京101416)
0 引 言
联合定轨是指对于具有星间链路的导航星座,联合星间测量和星地测量数据,通过统一融合处理,同时估计所有卫星的轨道参数。批处理定轨法是在观测结束后,结合某一单个历元所有观测信息求此历元状态变量的“最佳”估计。批处理方法的观测数据多,且具有统计特性,因此解算精度较高,但算法计算耗时,不适于作实时定轨[1-2]。利用批处理算法进行高精度的事后处理。
整网批处理定轨方法,即联合星间观测信息与星地观测信息,通过使用批处理算法进行整网平差的过程。在本文中基于星间星地链路的整网批处理定轨方法简称为星地整网定轨方法。
1 系统模型建立
1.1 星地伪距观测方程
假设测量过程中地面设备延迟已经过标校,则模型写为
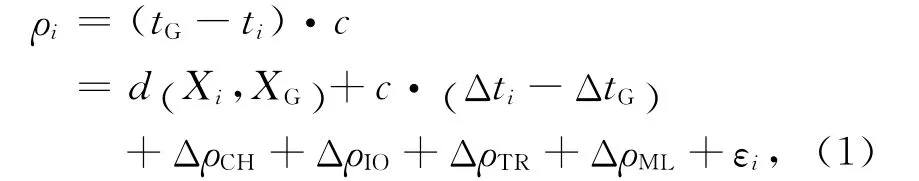
式中:ρi表示地面站G对卫星i的测量伪距;c表示光速;Δti表示卫星i的钟差;ΔtG表示地面站的钟差,由站间时间同步确定;ΔρCH表示卫星i发射机延迟差;ΔρIO表示电离层延迟误差;ΔρTR表示对流层延迟误差;ΔρML表示多径效应;εi表示接收机热噪声;d (Xi,XG)= [(Xi-XG)2+ (Yi-YG)2+(Zi-ZG)2]1/2表示两点之间几何距离;Xi、XG分别表示卫星i和地面站G在惯性系中的位置。
观测残差(O-C)表示为
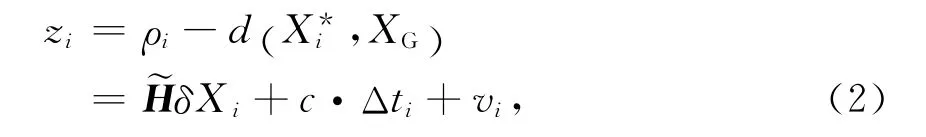
1.2 星间伪距观测方程
在此给出仅含卫星距离和钟差信息的改化伪距

式中:d (Xi,Xj)表示卫星i、j之间的几何距离;v表示观测误差,包括随机误差和未能消除的所有其它误差之和[3]。
观测残差(O-C)的形式为
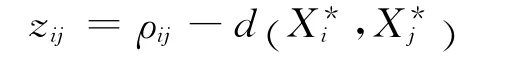
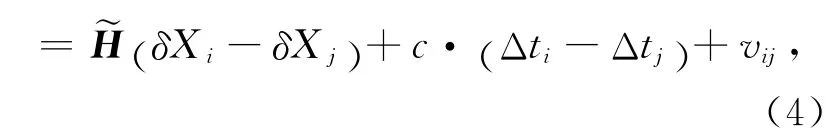
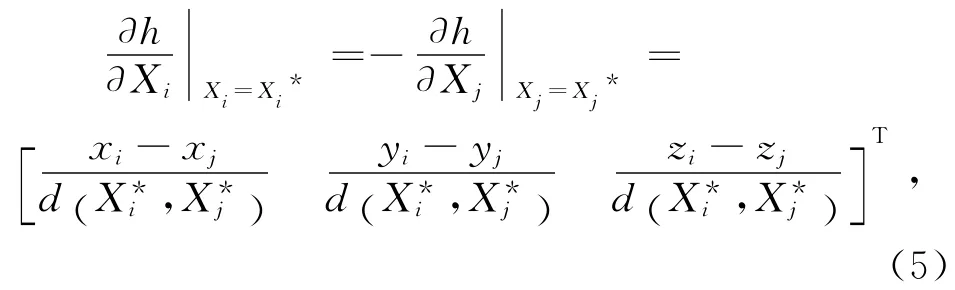
1.3 批处理算法
批处理定轨的基本方法是,将某观测弧段[t0,t]上得到m维观测值(包括星地和星间观测值)z=[z1z2…zm],通过状态转移矩阵归算到某一历元(如初始历元t0)。
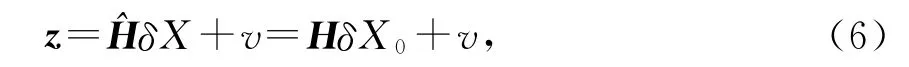
式中:z对应于式(2)或式(4)的星地或星间观测残差;X对应于轨道状态;因此,问题可化为求解t0时刻的最佳估计,这是一个典型的线性最小二乘问题。在工程应用中一般作Gauss-Markoff假设[4]
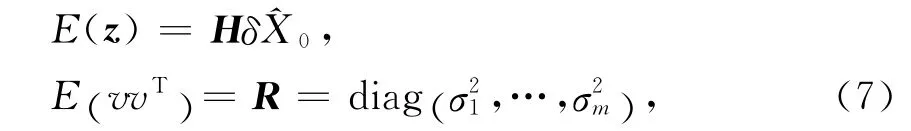
由于观测方程(6)中含有测量误差,工程中需要采用加权最小二乘估计方法,以保持尽量多的有用信息。问题描述为求x∈Rn,满足
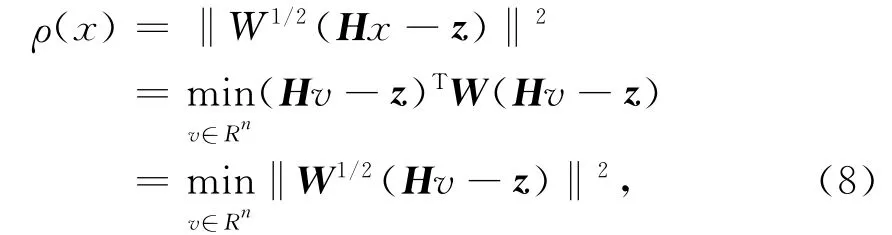
式中,W为实对称权矩阵,在应用中可取W=R-1.
式(8)的极小范数解为

式中,B=(W1/2H)-W1/2为矩阵H的加权广义逆。
2 批处理定轨计算过程
在进行导航卫星定轨计算过程中,所采用的状态方程和观测方程都是基于参考轨道进行线性化处理后的模型,所以其非线性部分会造成定轨结果的偏差。在批处理定轨中通过多次迭代来解决此问题。设置的收敛准则[5]为
1)卫星位置矢量最新估值的方差小于预先指定的判据POS.即
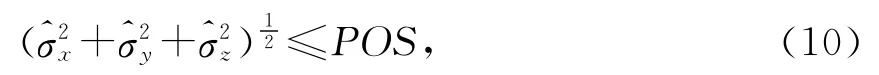
2)观测残差的均方差满足
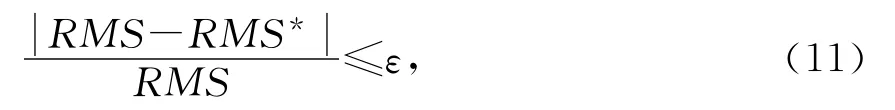
式中:ε为预先指定的一个小量;RMS为观测残差均方差;RMS*为观测残差均方差的线性预报值[6]。
RMS、RMS*定义为[6]
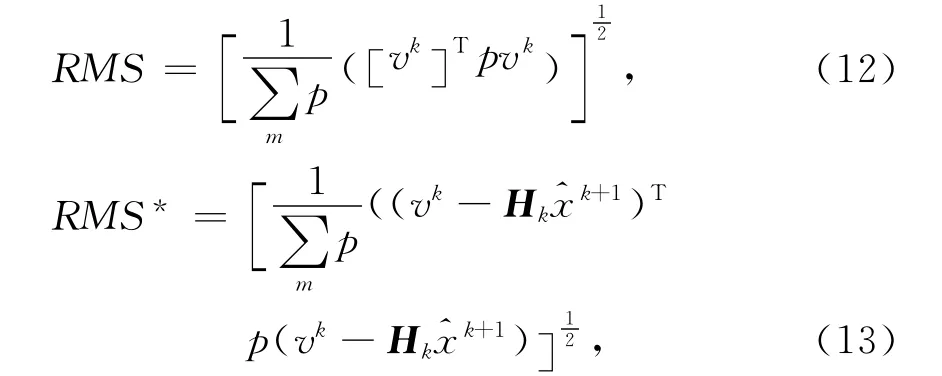
式中:vk为第k次迭代中观测数据的残差;为对参加估值的观测数据的权和。
当满足任意一个条件(10)或(11)时,再迭代一次即认为估计过程正常收敛而终止。设k+1次迭代收敛,则被估状态的最优估值为
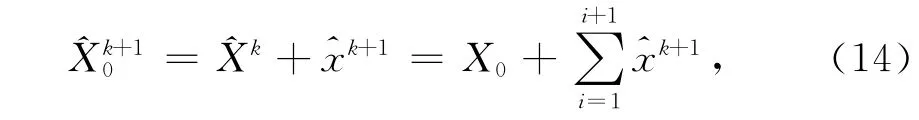
式中,X0为估计状态矢量的先验值。
参照批处理定轨的一般过程[7],整网批处理定轨的主要过程描述如图1所示。
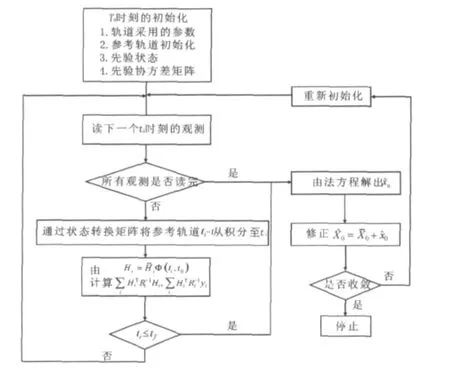
图1 批处理定轨算法流程
3 基于星地整网批处理定轨算法的仿真分析
3.1 仿真条件
星 座 构 型:Walker24/3/2:55°,轨 道 高 度:215 00km,轨道倾角55°[6].考虑星间测距误差0.5 m,波束角为30~60°;星地测距误差3.0m,截止高度角10°,不考虑传播时延及钟差。定轨弧长:7天。
3.2 仿真算例设计
在进行星地整网定轨计算时,观测数据的来源分为星地测距信息和星间测距信息。为分析星地测距信息的加入及地面区域布站的位置和数量对批处理定轨精度产生的影响,本章进行如下算例设计,如表1所示。

表1 星地整网批处理定轨仿真算例
在算例1与算例2中,采用传统地基方式进行定轨时分别采用了全球17测站和全球34测站的跟踪观测方案。其地面测站分布参照IGS全球测站分布位置设置,选取部分站位。其中全球17个测站代号分别为:ALGO、ALIC、ASPA、BAHR、BJFS、CIC1、DGAR、GLPS、GUAM、HARB、KOKB、LPGS、MAS1、OPMT、THTI、WUHN、ZIMM。全球34个地面测站代号分别为:ALGO、ALIC、ARTU、BAHR、BJFS、BRUX、CHUR、CIC1、CRO1、DARW、DGAR、GLPS、GUAM、GUAO、HARB、HOFN、KERG、KOKB、KOUR、KUNM、LHAZ、LPGS、MAC1、MANA、MAS1、MBAR、MDVJ、NKLG、NOT1、NRIL、OHI3、ONSA、OPMT、PERT。其具体地理坐标位置可在IGS网站中查询。
在分析地面测站的数量及分布对批处理定轨精度的影响时,选用了IGS在国内合作的5个地面测站。具体位置如表2所示。
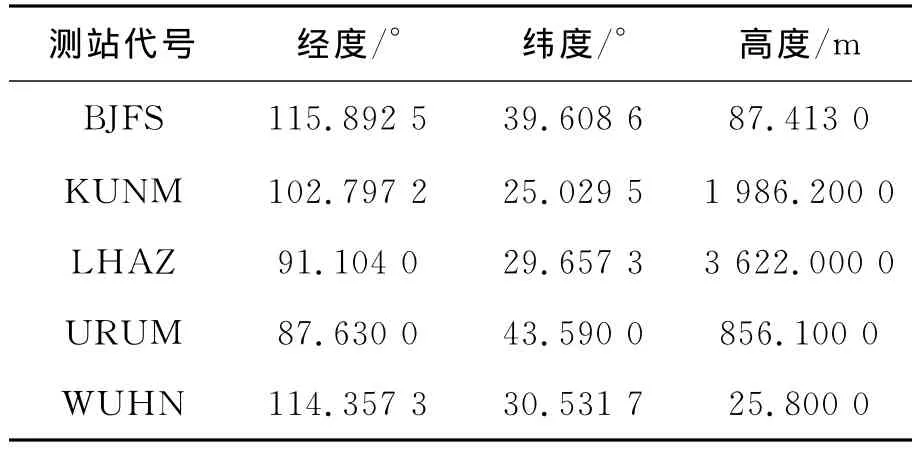
表2 国内5个地面测站地理坐标
3.3 仿真结果与分析
星地整网定轨的仿真结果以平均RMS值作为指标,其定义为
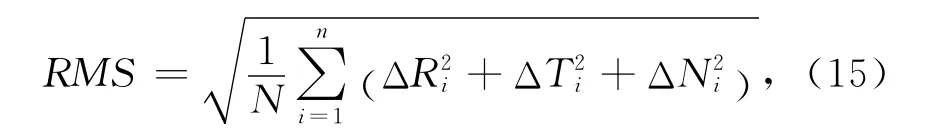
式中:N为观测历元总数;ΔR为轨道径向误差;ΔT为轨道沿迹向误差;ΔN为轨道法向误差。
算例1:图2示出了分别采用全球17个测站及全球34个测站进行传统地基定轨的第1天至第7天轨道RMS全星座统计值。条形图值代表所有全星座卫星轨道的径向、切向及法向三维RMS统计结果;“mean”表示了7天的平均值。图3示出了采用两种不同数量地面测站进行地基定轨的第1至第7天轨道RMS差值。
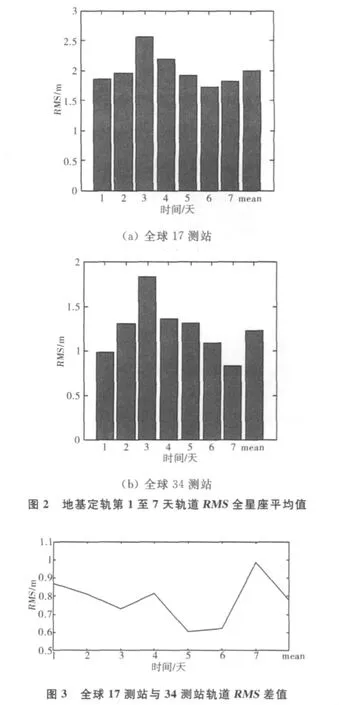
图4与图5示出了分别采用全球17个测站和34个测站进行传统地基定轨的第1天的所有卫星轨道RMS统计值。
图6示出了采用两种不同数量地面测站进行地基定轨的第1天轨道RMS差值
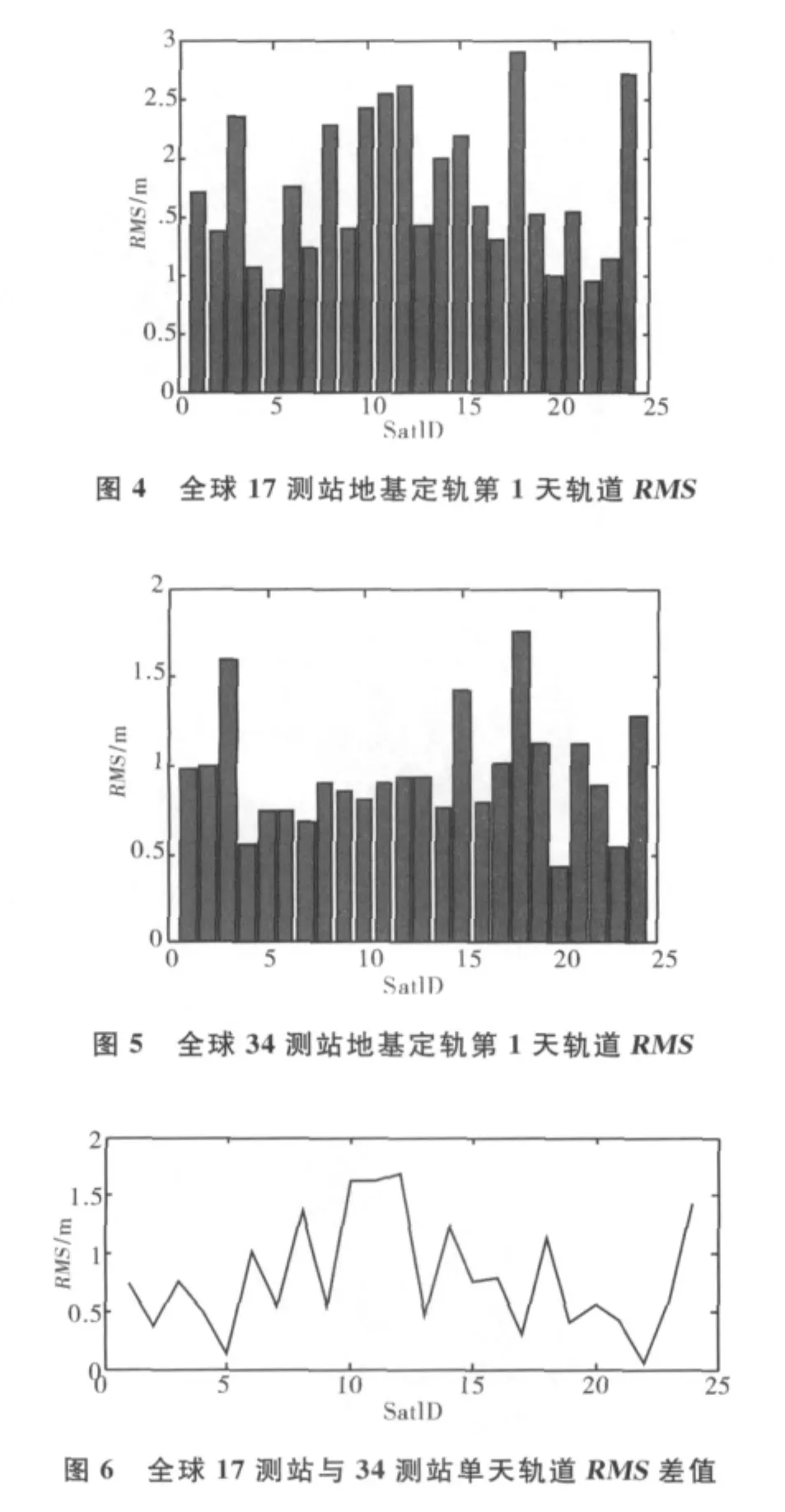
分析:从图中可以看出利用全球34测站进行传统地基定轨,其RMS精度明显高于利用全球17测站的地基定轨结果。34测站地基定轨的轨道平均RMS为1.24m;17测站地基定轨的轨道平均RMS为1.99m.这是因为当地面测站合理增多时,导航卫星的几何精度好,观测数据的增多使得空间约束增强。
算例2:为了分析星地整网批处理定轨精度,加入了星间观测信息,并对地面测站布设的不同组合进行仿真分析。具体方案设计及相应全星座RMS平均值如表3所示。

表3 星地整网定轨轨道RMS全星座7天平均值
图7示出了方案1~7对卫星进行星地整网定轨的第1至7天轨道RMS的全星座平均值。
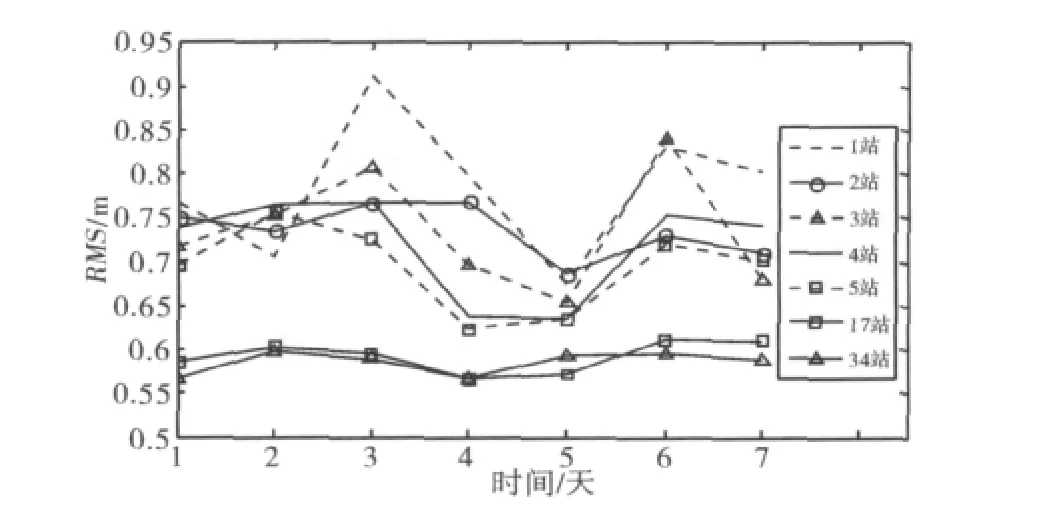
图7 整网定轨第1至7天轨道RMS全星座平均值
分析:从以上图、表可以看出:
1)全球分布测站及国内局域测站的整网定轨精度都较高,轨道RMS均优于1.0m,相对于全球34站和17站的传统地基定轨结果有较大提高。由于星间链路信息加强了卫星沿迹向与法向的几何约束,定轨误差显著减小。
2)全球分布测站的整网定轨精度要稍高于国内测站整网定轨精度,国内局域测站进行整网定轨的各种方案结果精度相差不大。在相同的星间链路构型中,相比于全球布站,局域布站的几何精度相对较差,因此精度稍低。
3)国内局域测站进行整网定轨,其7天平均RMS值度与测站数无显著对应关系,但是地面测站越多,单天定轨结果差异越小,表现越稳定。
4 结 论
导航星座卫星对轨道确定的精度和自主性要求较高,采用传统的地基定轨方法已不能满足需求,但若完全依靠星间相互测量伪距定轨则又存在星座网的基准秩亏问题。提出了基于星间星地链路的整网批处理定轨方法。由仿真结果可知在地面系统支持下,星地联合整网估计的精度远高于传统定轨精度,定轨精度主要取决于星间观测的精度。适当增加地面测站时,导航卫星的几何精度好,观测数据的增多使得空间约束增强,可以提高定轨精度。
[1] 朱 俊,廖 瑛,文援兰.基于星间测距和地面发射源的导航星座整网自主定轨[J].国防科技大学学报,2009,31(2):15-21.
[2] 胡小平.自主导航理论与应用[M].长沙:国防科技大学出版社,2002.
[3] 周建华.序贯处理与成批处理在定轨应用中的一些问题[J].测绘学,1993,22(2):142-148.
[4] ANANDA M P,BERNSTEIN H,CUNNINGHAM K,E,et al.Global positioning system(GPS)autono-mous navigation[C]//IEEE Position Location and Navigation Symposium,las Vegas,1990:435-455.
[5] 林益明,秦子增,初海彬.基于星间链路的分布式导航自主定轨算法研究[J].宇航学报,2110,31(9):2088-2094.
[6] OLIVE M,EBERHARD G.Satellite orbits Models,methods,and application[M].2nd ed.Verlag Berlin Heideberg New York:Springer,2001:208-218.
[7] WEN Yuantan,ZHU Jun,LI Zhi,et al.Simulation and analysis of integrated orbit determination of satellites constellation[J] .Journal of Astrooeutics,2009,30(1):155-163.
[8] 张育林,范 丽,张 艳.卫星星座理论与设计[M].北京:科学出版社,2008.

