GPS短边方位角测量精度定量分析研究＊

曹金国，廖望东，李建伟，戴山岭

（96633部队，北京100096）

0 引 言

全球定位系统（GPS）由于具有高精度、全天候的相对定位功能，在测量中得到了广泛应用，特别是专用工程各类方位边的大地方位角测量方面，更是体现了其巨大的应用价值。长期以来，短边GPS方位角的测量精度评定方法是困扰作业单位的一个重要难题。传统的精度评定方法是将天文方法测得天文方位转化为大地方位角，作为已知值，比较GPS测量的短边大地方位角，对成果进行简单地精度估计，未实施天文测量的方位边则无法进行评定精度。作业前通常采用接收机的标称精度设计GPS方位边的边长，将其标称精度的固定误差全部分配在影响方位的横向方向上。标称精度衡量的误差是基线长度误差，方位角的误差实际上与基准点至方位点的横向误差有关系。如何从三个向量中准确地分离出横向误差，从而估计出每条方位边的实际精度，对于外业队方位测量中实时掌握其精度具有实际意义。

1 方位边两个点由地心坐标向站心坐标的转换

为了精确计算方位点相对于基准点的横向误差，首先将空间直角坐标转化为以方位边的基准点为原点的站心坐标［1］。如图1所示，假设地面两点i、j的大地空间坐标分别为（X，Y，Z）i和（X，Y，Z）j，建立以地面点i为原点的站心坐标系，U轴与i点的椭球法线方向重合，指向椭球外；N轴垂直于U轴指向北极，E轴垂直于（N，U）决定的平面，并与U、N轴构成左手坐标系。

图1 地心坐标系向站心坐标系的转换关系

j点的站心坐标（N，E，U）为

式中，M为坐标转换的系数矩阵，即

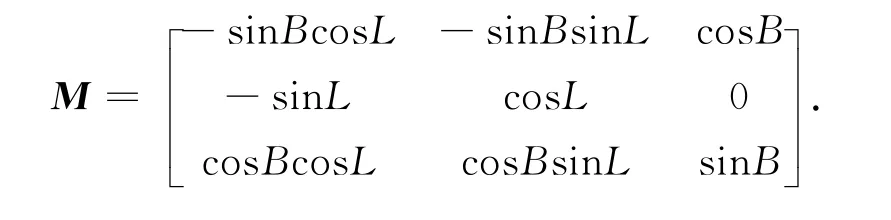
（ΔX，ΔY，ΔZ）为i、j两点间向量，则i、j两点间的大地方位角A的计算公式为

为了估算方位的精度，需要将式（2）线性化，可以得到

通过式（3）就可以估算方位角的精度，可以看出精度大小仅取决于N和E，而N和E实际上与测站点的位置、基线长度等有关系。为了估算每条基线的方位精度，需要知道N、E的协方差。

2 N和E的协方差确定

GPS基线解算时，每条基线的解算结果中都提供了这条基线三个分量的协方差，采用该协方差就可以精确的估计出方位的精度，考虑到基线解算时三个分量的协方差相对于地心坐标系统，需要根据协方差传播定律将其转化为站心坐标系的协方差［2］。假定GPS基线解算时导出（ΔX、ΔY、ΔZ）的协方差为

根据协方差传播定律［2］，可以得到（N，E，U）的协方差，即

3 方位边的方位角精度估算

将式（5）得出矩阵的相应对角元素带入式（3），得到i、j两点的方位角精度计算公式为

若观测了两个时段，得到的角度为A1和A2，精度为m1、m2，两个时段属于独立观测，各时段方位边方位角的权可以这样定义

则两个时段方位边方位角的平差值为

利用式（8）按照误差传播定律可以导出平差后方位边的中误差为

4 计算结果

4.1 各时段观测结果统计

对某检验场的GPS方位边观测数据按照本文的精度估算方法进行了试验，并且与已知方位角进行了比对。由于专用工程GPS观测时关心的是短边方位的精度，所以仅统计了边长100～300m左右的数据计算结果，该GPS数据观测时段长度为1h，观测了2个时段。2011年第1组第1、2时段各方位边的精度统计分别如表1和表2所示，2011年第2组第1、2时段各方位边的精度统计如表3和表4所示，2012年第1、2时段各方位边的精度统计如表5和表6所示。

表1 方位边精度计算结果以及与已知方位角之差

表2 方位边精度计算结果以及与已知方位角之差

表3 方位边精度计算结果以及与已知方位角之差

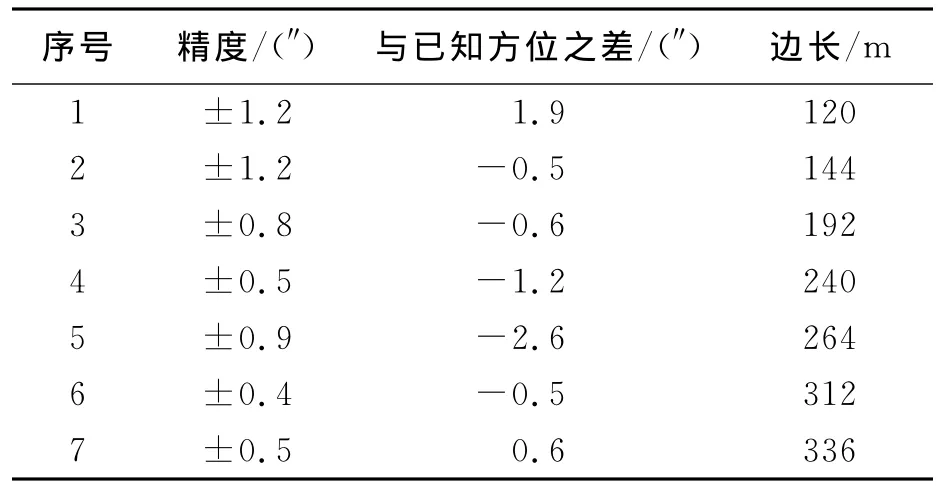
表4 方位边精度计算结果以及与已知方位角之差

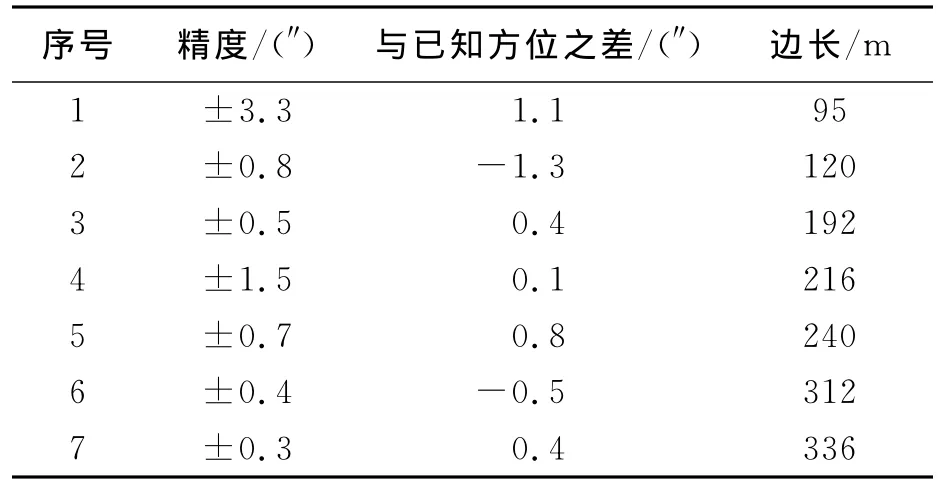
表5 各条方位边精度计算结果以及与已知方位角之差

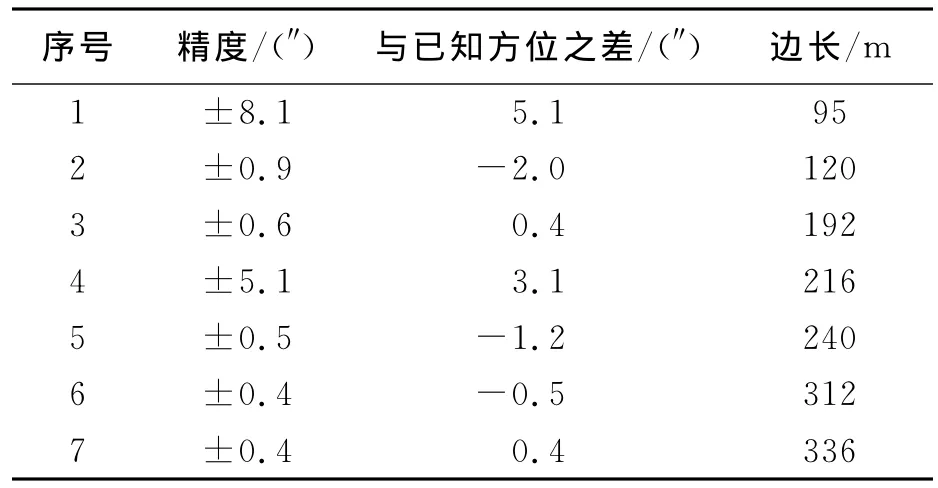
表6 方位边精度计算结果以及与已知方位角之差

4.2 2个时段方位角平差精度统计

对2个时段的检验结果的方位边方位角精度进行了精度估算，并且与已知方位角进行了比对。2011年的两组仪器检验结果分别如表7和表8所示，2012年的检验结果如表9所示。

表7 2个时段方位角平差后精度及与已知方位角之差

表8 2个时段方位角平差后精度及与已知方位角之差

表9 2个时段方位角平差后精度及与已知方位角之差

5 数据分析

地心坐标系中三个分量与站心坐标系的三个分量的对应关系与测站位置有关，位于该检验场时对应关系为ΔX≈ΔE、ΔY≈ΔH、ΔZ≈ΔN，而且GPS定位时高程精度大约是水平精度的2倍，所以转换为站心坐标系后能够很好衡量其误差比例关系。例如2011年的第一组数据中地心坐标系的3个分量的误差转换为站心坐标系后的3个分量的误差如表10所示。

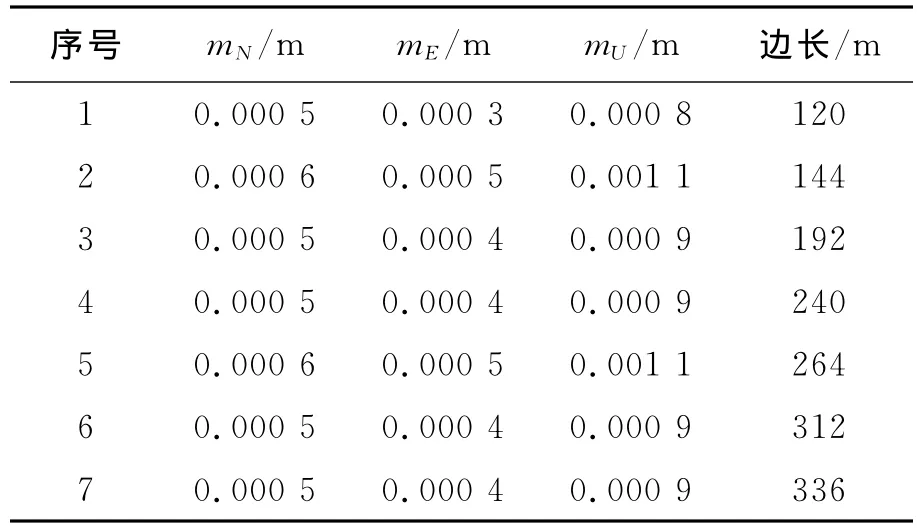
表10 站心坐标系中3个分量的精度结果

由表10可以清楚的看出水平精度和高程精度的关系，即高程精度大约是水平精度的2倍。所以说将地心坐标系中三个分量误差转换站心坐标系后，由N和E两个方向的误差进行方位精度的计算方法是准确可行的。

6 结 论

1）从表7、表8和表9的统计结果来看，实测的短边方位角与已知方位角之差不大于3倍的中误差，说明该精度统计方法是可靠的。在不考虑相位中心偏差和仪器对中误差的情况下，采用该方法对实测的GPS短边方位角进行精度估计。如果不满足使用精度要求，必须进行补测或者重测。

2）使用中还应考虑的天线的对中误差，对中误差对方位的影响可以采用以下公式估计mA＝，式中的e为对中误差，s为边长，ρ＝206 265″.为了提高天线对中的精度，测量前应该精确检校仪器对中设备，测量时可以采用强制对中或时段间重新架设三脚架的方法，来减弱仪器对中误差的影响。

［1］ 刘大杰，施一民，过静珺.全球定位系统（GPS）的原理与数据处理［M］.上海：同济大学出版社，2006.

［2］ 王新洲，陶本藻，邱卫宁，等.高等测量平差［M］.北京：测绘出版社，2006.