GPS天顶对流层延迟计算方法研究*
张婷婷,徐子乔,董思学
(1.江苏省新沂市房产服务中心,江苏 新沂221400;2.中国矿业大学 环境与测绘学院,江苏 徐州221116)
0 引 言
对流层延迟是影响GPS定位的主要误差源之一,它分为由干燥大气引起的干延迟和由水汽引起的湿延迟两部分。目前,诸多学者提出的多种全球对流层模型,比较常用的有Saastamoinen模型、Hopfield模型和EGNOS模型等。这些模型一般能把干延迟改正到90%以上,由于湿延迟随机性比较强,只能改正20%左右。随着用户对GPS定位精度要求的提高,如何更好地削弱对流层延迟误差,提高GPS定位的精度,己经成为一项亟待解决的任务[1]。
1 GPS对流层延迟基本理论
对流层延迟一般指中性大气层对电磁波的折射[2-3]。GPS数据处理中,如果把所有信号传播方向的斜路径延迟都当做参数代入观测方程的时候,会造成观测方程的秩亏。因此,有学者提出将对流层延迟以天顶方向延迟与映射函数相乘的方式来表示。由于映射函数是卫星高度角的函数,这就等同于把天顶延迟与斜路径延迟关联起来,任意方向的对流层延迟均与天顶延迟相关。

式中:ΔTrop为斜路径延迟;ΔWet为天顶湿延迟;MWet为湿映射函数;ΔDry为天顶干延迟;MDry为干映射函数。在实际应用中,人们常常采用的对流层延迟模型是Hopfield模型和Saastamoinen模型,而GMF映射函数和VMF1映射函数是被主流解算软件所选用的映射函数。
1.1 Hopfield模型
Hopfield模型是由全球气象探测资料进行分析建立的,在该模型中大气分层仅分为对流层和电离层两层。在对流层中,大气温度下降假设成一个常数β;根据观测资β≈+6.5℃/km.模型采用以下公式

式中:HT、HW、P0、T0、e0和h分别为干大气层顶高(m)、湿大气层顶高(m)、地面气压(mbar)、地面温度(T)、地面水汽压(mbar)和测站在大地水准面上的高度(m).常参数k1=77.6K/mbar;k2=71.6K2/mbar;k3=3.747×105K2/mbar.
而干、湿大气层顶高(HT、HW)和地面水汽压e0计算:


1.2 Saastamoinen模型
在Saastamoinen模型中,把地球大气分成三层:第一层是从地面到10km左右高度处对流层顶的对流层,这一层中的温度下降率假设为6.5℃/km;第二层是从对流层顶到70km左右的平流层,其中温度假设为常数;第三层是平流层以外的电离层。

式中:eW为水汽压(单位是mbar);P为干大气压(单位是mbar),把测站位置和高程作为参数,Saastamoinen模型下的天顶延迟为

式中:φ为测站纬度(单位为(°));H为测站高程(单位为km)。
1.3 GMF映射函数
GMF模型是由Boehm等人提出的一种新的全球映射函数,其投影函数是基于全球ECMWF数字气象模型(NWM)数据建立的。干延迟包括与测站高程有关的改正,反映了大气密度随高度增加而减少的变化率。在GMF模型中输入的参数是年积日、测站经纬度和测站高程。
干分量的计算为

式中:

湿分量的计算为

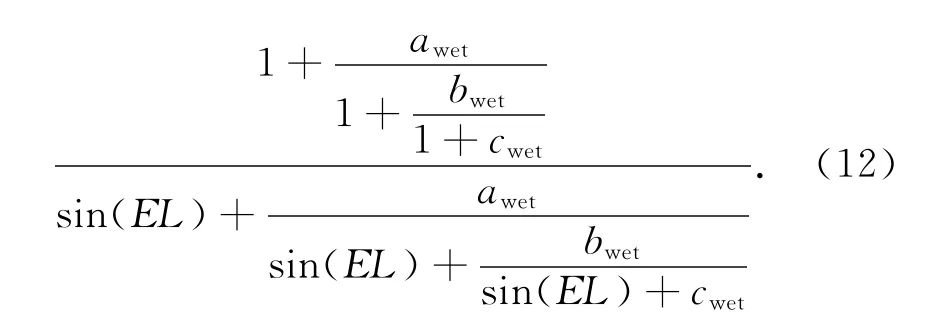
1.4 VMF1映射函数
Boehm等人在2004年利用ECMWF提供的初始角3.3°湿折射率、6h分辨率的等压面数据,使用射线跟踪方法构建了近实时动态映射函数VMF1,VMF1依然采用三项连分式表达式,不同之处在于干湿映射项中系数的选取方法。在VMF1中,用户可以通过在从奥地利维也纳理工大学大地测量研究所网站下载全球格网点adry和awet(时间延迟约34h)。再采用一定的内插算法来求取测站的adry和awet值。另外,在该映射函数中,湿映射项系数bwet与cwet,分别取常数0.001 46和0.043 91,干映射项系数bdry和cdry是利用ECMWF提供的40年观测数据用水平约125km的分辨率采用球谐函数展开式计算得到,其中bdry取常数0.002 9,cdry计算公式如式(13):

式中,φ为测站所在纬度。
当测站在北半球时,c0=0.062,c10=0.001,c11=0.005,φ=0;当测站在南半球时,c0,c10=0.002,c11=0.007,φ=π.
2 对流层干、湿延迟分析
对流层处于一个不太稳定的状态,对流层延迟的值也是一个具有波动性的数值,寻找对流层延迟波动的规律是研究对流层一个重要思想和方向。对流层的天顶方向较其他方向具有一定代表性和确定性(忽略了天顶角等因素的影响),所以,对天顶对流层延迟的研究不仅能降低很多不确定因素的影响,而且还不失其真实性[4]。
实验数据选用KUNM、WUHN、SHAO、WTTF、XIAN等IGS跟踪站2008年中部分年积日(DOY)的观测数据。
2.1 天顶对流层干延迟的年分布特征
天顶对流层干延迟作为天顶对流层延迟的一部分,它相比湿延迟部分具有明显的稳定性。
图1与图2为其中两站的干延迟值图,很明显如果把全年干延迟全部反映出时,会呈现出一个类正弦曲线的分布值图。这说明各个测站的天顶对流层干延迟都是以年为周期变化(一些研究文献表明,干延迟在每一天中还会有一个小周期的波动,这里不作细致的研究)。结合各个IGS站的资料,从图3可以分析得出以下结论:

1)从SHAO站和WUHN站分析结果表明,在纬度和测站高程大致相等时,经度对天顶对流层干延迟值影响较小;
2)由1)中结论为依托,对比KUNM站和TWTF站,因为KUNM、TWTF纬度大致相等,高程大约相差1 685.809m,干延迟值相差平均为550mm,说明高程对天顶对流层干延迟值影响很大,且高程越高干延迟值越小;
2.2 天顶对流层湿延迟的年分布特征
相对于干延迟,湿延迟由于受到水汽等易变因素影响,往往呈现出波动大,不稳定,难预计等特点。将以5个IGS站2008年某些年积日数据为实验数据,对这5个IGS跟踪站所在地区的天顶对流层湿延迟进行分析,尝试寻找和总结其中的一些规律,如图4~7所示。可以明显看出:
1)3个IGS站均是冬季天顶湿延迟值较小,夏季天顶湿延迟值较大,结合推测的湿项延迟与水汽压力有关,便可以得出水汽密度越大的地区湿延迟值越大;
2)各地天顶湿延迟值虽然大致规律相似,但是对比图7不难看出在细节处,SHAO站只在夏季ZWD值略高于TWTF站,且TWTF站夏、秋两季ZWD值相差不大,对此,推测这些ZWD的特殊分布可能与各地区的气候特征有关,作为推测的验证,可以下载某地中海气候地区的IGS站观测数据进行验证。


3 干延迟区域建模[5-6]
随着RTK技术的快速发展和成熟,用户已经不只仅仅满足于它快速和方便定位的优点,更高精度的需求已经愈发凸显,普通民用用户也希望获得较高精度的定位数据,因此,建立一种能快速推算出具有一定精度的对流层延迟模型具有实际意义。
假设拥有4个IGS站(KUNM、SHAO、TWTF、XIAN)对流层观测数据,推算某个不具备气象观测条件的临时观测站(WUHN).
3.1 区域模型函数的建立
根据前面两节基础理论,尝试着列出一些能够反应天顶对流层干延迟(ZHD)与时、空因素数值关系的方程。
1)根据测站位置与年积日因素来建立的模型函数:

2)考虑到已经验证出经度对ZHD影响不大而改进的模型函数:

3.2 区域函数模型的选择
根据上面建立的两种模型,代入已知测站的时、空数据,用迭代法求取系数。
本节实验数据选择上述5个IGS国际跟踪站2008年部分年积日数据(平均分布在春夏秋冬4个季节)。通过GAMIT对数据进行较高精度处理,抽取出4个基准站(KUNM、SHAO、TWTF、XIAN)数据建模,以观测站(WUHN)实测数据来检验其精度。
解算求取的结果:
模型1函数RMS=3.914 423 654 938 03,模型2函数RMS=4.152 498 375 864 36.各项系数如表1所示。

表1 两个自建区域模型函数参数
结合本章前面分析得到的结论,做出分析:
1)模型1均方差RMS值较模型2更小,从拟合数据上来看,拟合效果比较理想;
2)如果结合本章前面小节的分析结论,模型2的参数形式更符合分析结论,即高程方向距离影响比纬度方向距离影响更大(|a3|>|a1|).
把求解后的参数代入原模型,再通过验证测站WUHN站数据解算,求WUHN站的推测ZHD值。假设以实测数据解算得到的值为真值,模型函数推测值为实验值,则两数值之差可认为是偏差值。可以看出模型1函数平均偏差值在10 mm左右,且偏差比较稳定;模型2函数平均偏差值也在10mm左右,但偏差波动较大,最大值为23.373 146mm,最小值则只有0.128 922mm,模型2部分拟合程度明显好于模型1,如图8所示。
两个模型函数各自具有其优点,但精度低的缺点明显。本节实验所建立的两个模型虽然能达到1cm的精度,满足普通用户的快速定位要求,但对于精度要求较高的定位和应用将无法得到满足。下面,对于出现这种缺点的原因进行分析:

图8 模型1和模型2推测值与实测值对比图
1)各个基准站之间基线长度过长。最长基线KUNM-SHAO约为1 925km,最短基线SHAOTWTF约为690km,大区域的巨大空间变化,降低了模型对空间要素的灵敏度。因此,基线过长、拟合区域过大是导致模型精度低的主要原因之一,相比之下,当采用某省或者某市CORS站数据进行拟合时,相信精度能得到很大的提升。
2)解算各站的观测数据量少。本实验只选用了2008年中27天的观测数据,仅为一年数据的1/13.5.假想当采用全年观测数据进行拟合,则模型精度也可能将得到很大提升。
4 结 论
通过介绍大气对流层延迟理论,特别是Hopfield模型、Saastamoinen模型以及GMF、VMF1两个映射函数。结合大气延迟理论,通过5个IGS跟踪站一年中部分年积日观测数据计算,总结出各IGS站所在地,干、湿延迟的年变化规律。依据这些规律性结论,拟建区域对流层干延迟模型,并以GPS解算数据为真值,检验了模型的可行性[7]。但由于实验数据选择的IGS跟踪站基线过长,数据量太少,总结的规律和结论偶然性太大,导致区域模型精度受到很大影响,为了更好的验证所建立的模型的可行性,需要采用基线更短、测量时间更长的数据进行研究,使这些结论更具说明性,更接近真实情况。
[1] 张 勤,李家权.GPS测量原理及应用[M].北京:科学出版社,2005.
[2] 严豪健,符 养,洪振杰.现代大气折射引论[M].上海:上海科技教育出版社,2006.
[3] 洪卓众.区域对流层模型在地基GPS气象学中的应用研究[D].长安大学,2011.
[4] 薛志宏.GPS随机软件中的对流层模型及对基线处理的影响[J].全球定位系统,2007,33(6):18-21.
[5] 戴吾蛟,陈招华,匡翠林.区域精密对流层延迟建模[J].武汉大学学报,2011(4):36-40.
[6] 王 勇,焦 健,曾琪明.基于不同地形的GPS对流层延迟插值方法研究[J].大地测量与地球动力学,2010(6):30-33.
[7] 任亚飞,柯熙政.GPS定位误差中对流层延迟的分析[J].西安理工大学学报,2006(4):407-410.
——环地平弧&环天顶弧

