自适应滤波在GPS测速中的应用*
仇立成,祝程程
(武汉大学测绘学院,湖北 武汉430079)
0 引 言
利用GPS测速是常用的一种方式,然而GPS测速误差中包含有卫星星历误差、电离层、对流层延迟以及多路径效应等较多误差,对GPS的测速精度有着十分重要的影响,减小其误差的一种重要的方法即为卡尔曼滤波。采用GPS测量中的多普勒测速方法对汽车进行实地测速分析,比较了标准卡尔曼滤波以及自适应滤波两种方法的效果,得出了自适应滤波结果要优于标准卡尔曼滤波的结论。
1 GPS动态测速数学模型建立
1.1 GPS定位方程
由于采用的是多普勒测速方法,所以仅就此方法做详细介绍。给出GPS伪距定位方程[1]为

式中,卫星观测瞬间在空间的位置为Xi,Yi,Zi;接收机观测瞬间在空间的位置为X,Y,Z;δtR为接收机钟差;δtiS为卫星钟差;(Δion)i和(Δtrop)i分别为电离层和对流层的影响。
1.2 多普勒测速
由于GPS载体和GPS卫星之间存在相对运动时,接收机收到的GPS载波信号频率,与卫星发射的载波信号的频率不同,其间的频率差,称为多普勒频移。频移的大小与接收机和卫星之间距离的变化率有关[2]为

式中:df为多普勒频移,即已知观测量;˙ρ为接收机和卫星之间的距离变化率;f为卫星发射的载波频率;c为光速。
对式(1)求导,并忽略卫星坐标、载体坐标误差、电离层、对流层和测量噪声的影响,得到实用误差方程为

2 自适应滤波方程的建立
2.1 状态方程的建立
为了确定其位置、速度,其状态变量选取为

此处采用E,N,U导航坐标系,其中,p,v,a,ε分别为位置,速度,加速度和位置误差,ε用一阶高斯马尔科夫过程表示为

式中:τ为相关时间常数;ω为高斯白噪声。
状态方程取为机动载体的“当前”统计模型[3]

式中:

2.2 量测方程的建立
将GPS接收机的定位结果p,取为观测量,它包括了真实的状态变量p,一阶高斯马尔科夫过程ε,以及量测误差ωK.可写为
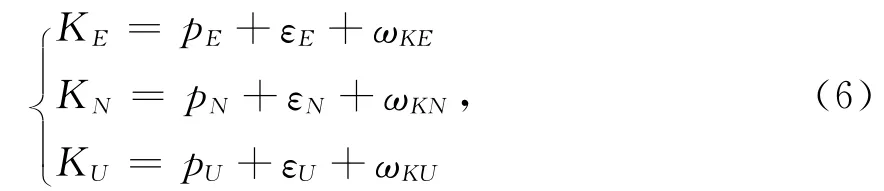
写成矩阵形式为

式中:Z=[KE,KN,KU]T;X=[p,ε];V=[ωKE,ωKN,ωKU]T.
2.3 自适应滤波方程的建立
下面给出滤波的计算过程[4]:
一步预测方程:

状态估计方程:

求取增益矩阵:

一步预测均方误差:
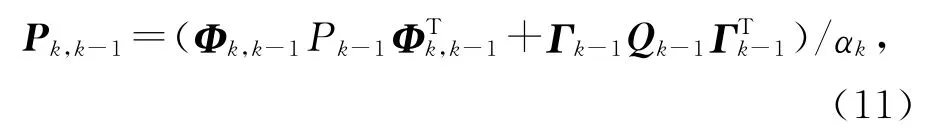
估计均方误差:

式中,Qk-1和Rk分别为系统噪声方差矩阵和量测噪声方差矩阵。
此处的自适应因子αk可取渐消因子的倒数[5],即

式中,tr[·]表示矩阵的迹。

3 实验数据解算及分析
实验采用加拿大NovAtel公司生产的SPANSE双频接收机[6],它是NovAtel最新的支持SPAN技术的产品,它为用户提供了IMU接口,原始测量数据输出、多种通信协议、GPS和GLONASS、可实现长距离的RTK功能、可支持双天线测向技术、SD卡数据存储功能、支持以太网通信等[7],此次实验采取车载模式,行驶过程约为1h.
表1、2示出了仪器性能指标和滤波量测噪声方差。

表1 仪器部分性能指标

表2 量测噪声方差
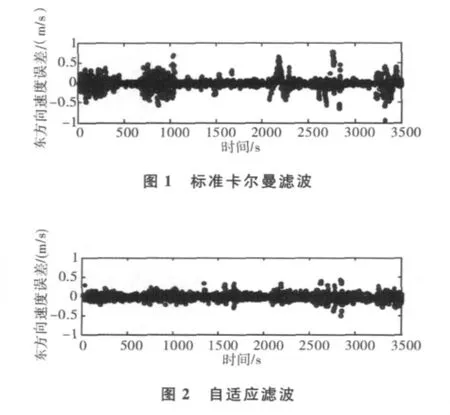
限于篇幅所限,图1、2示出了具有代表性的东方向速度测量的误差值,分别为标准卡尔曼滤波和自适应滤波情况下的误差图。
对这些数据计算,剔除粗差,可得具体的均方根误差值,如表3所示。

表3 两种滤波方法的测速精度
通过以上数据分析,得到以下结论:
1)通过标准的卡尔曼滤波可以使GPS测速结果精度有所提高,但是其并不能控制载体运行扰动异常误差的影响。比如当载体本身发生突变或产生较大扰动加速度时,载体的先验状态方程不可能可靠地预测载体的未知状态,或者卡尔曼滤波受到参数初值不可靠影响,则最终解必然受到歪曲。从图1的较多历元中,可以看出有许多时刻解的波动较大。
2)从图2中可以看出,与标准的卡尔曼滤波相比,自适应滤波能够克服掉上面所说的标准卡尔曼滤波的这些缺点,从而使得解的结果更加符合载体的实际运动状况,得到较好的测速精度。
4 结 论
1)由于GPS测速的各种误差的影响,尽管自适应滤波的精度优于标准卡尔曼滤波,但是仍然是分米级的误差,无法达到厘米甚至更高的精度,因此,对这种方法仍有改进和完善的余地。
2)总之,自适应卡尔曼滤波可以同时抑制状态的估计误差和扰动误差的影响,得出更接近实际运动状态的最优估计值,是一种行之有效的滤波方法。
[1] 李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005.
[2] 徐绍铨,张华海,杨志强,等.GPS测量原理及应用[M].3版.武汉:武汉大学出版社,2008.
[3] 房建成,万德钧.GPS动态定位中自适应卡尔曼滤波模型的建立及其算法研究[J].船舶工程,1997(2):36-40.
[4] 泰永元,张洪钺.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998.
[5] 夏启军,孙优贤,周春晖.渐消卡尔曼滤波器的最佳自适应算法及其应用[J].自动化学报,1990,16(3):210-216.
[6] WU F M,YANG Y X,ZHANG L P.A new fusion scheme for accuracy enhancement and error modification in GPS/INS tight integrated navigation[J].Survey Review,2012,44(326):208-214.
[7] LUO Yong,WU Wenqi,RAVINDRA B.A simplified baseband prefilter model with adaptive Kalman sdaptive filter for ultra-tight COMPASS/INS integration[J].SENSORS,2012,12(7):9666-9686.

