互相关干扰下微弱GPS信号的直接检测算法＊

董 翔，赵振维，刘世萱，王 波，刘海丰，林乐科

（1.中国电波传播研究所，山东 青岛266107；2.山东省海洋环境监测重点实验室，山东 青岛266001；3.山东省科学院海洋仪器仪表研究所，山东 青岛266001）

0 引 言

GPS卫星发射的信号属于码分多址（CDMA）体制，其L1载波（1 575.42MHz）上调制着码速率为1.023MHz的伪随机码（称为C／A码）以及50 bit／s的导航数据，该信号体制对于热噪声具有良好的抑制效果。但是在复杂环境下（如森林、城市楼宇、室内等）的 定 位［1］、GPS无源雷达探 测［2－3］、GPS反射信号遥感［4－5］等强弱信号共存的场景中应用时，GPS接收机面临着一个棘手的问题：强信号干扰下微弱信号的检测。不考虑人为干扰的情况下，这种强信号的干扰是指GPS C／A码的自相关干扰以及互相关干扰。

由于GPS互相关干扰属于结构性干扰［6］，无法通过延长相干积分时间来消除。目前，抑制GPS互相关干扰的方法主要有：1）消去法，如SIC、PIC、DPIC［7］等，该类方法主要通过捕获和跟踪强干扰信号获得干扰信号参数，利用这些参数重构干扰信号，并从输入信号中减去该干扰信号，最后对剩下的相对“纯净”的信号进行二次捕获。2）投影法，如子空间投影法、减去投影法［8］等，该类方法主要利用C／A码之间的近似正交特性，构造干扰信号的子空间，然后将强信号分量消掉。此外，还有一些其它方法，如自适应约束正交法（AOUC）［9］、Q路滤波法［6］等。这些方法虽然能够在一定程度上消除掉一部分互相关干扰，但也存在各种缺点：消去法严重的依赖于干扰信号参数估计的准确性；投影法需要矩阵求逆运算，且对于接收机量化位数有较高要求等。

基于GPS互相关干扰模型，详细分析了强弱信号间的相对载波多普勒频移（RDC）对互相关干扰的影响。在此基础上研究了一种互相关干扰下微弱GPS信号的直接检测算法，该算法不需要消除强干扰信号，而是通过分析相关值在每个多普勒仓的特性来找到弱信号的自相关峰值，从而实现互相关干扰下的微弱GPS信号直接捕获。

给出了GPS互相关信号模型及其特性，分析了强弱信号间的RDC对于互相关干扰的影响，并在此基础上给出了基于RDC的互相关检测算法，最后利用仿真数据对算法进行了验证和分析。

1 GPS互相关干扰模型

GPS接收机接收到的中频采样信号模型可以表示为

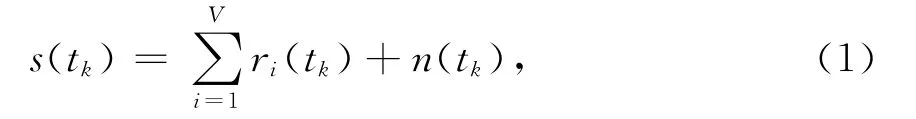
式中：V代表可视卫星的数目；n（t）表示高斯白噪声。其中第i颗卫星在采样时刻tk的表达式可以表示为

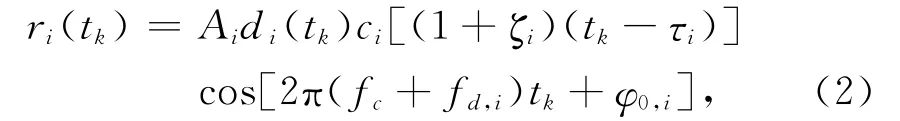
式中：Ai为信号幅度；di是导航数据位；ci代表PRN码；τi和φ0，i分别表示码相位和载波初始相位；ζi和fd，i分别代表由卫星及接收机的相对运动所产生的码速率扰动和多普勒频移。

GPS接收机对某颗卫星的捕获实质上是一个在码相位和多普勒频移上的二维搜索过程，即利用本地复现的C／A码和载波对接收信号进行相关匹配滤波，假设第i颗卫星的本地复现采样信号为

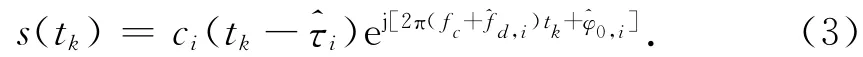
令相干积分时间为T，其对应的采样点数为K，则相关器输出的信号表示为［10］

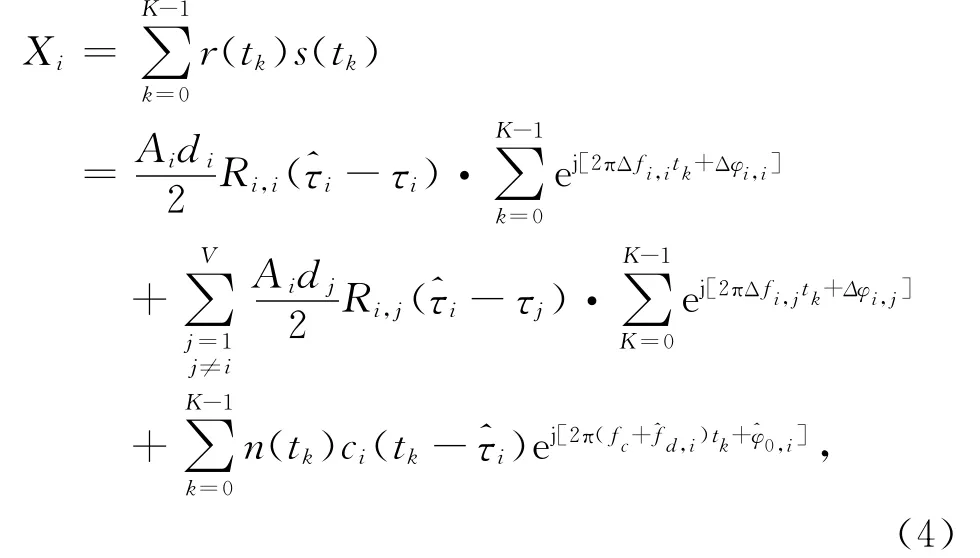
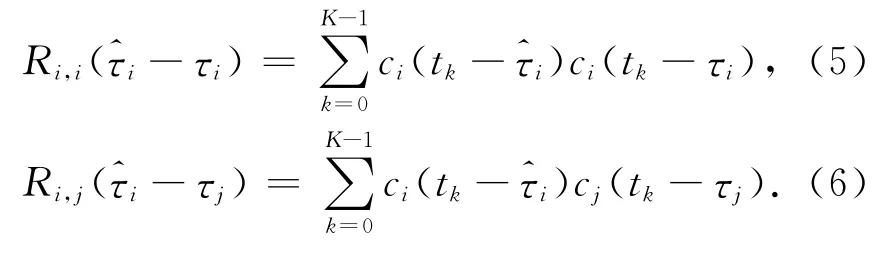
式（4）等号右侧的第一、二和三项分别表示信号自相关项、互相关干扰项以及噪声项，Δfi，j表示第i颗卫星和第j颗卫星之间的相对多普勒频移。

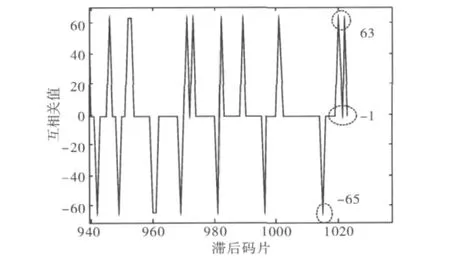
图1 GPS的C／A码互相关取值示意图

2 RDC对于互相关干扰的影响

讨论式（4）等号右侧的第二项即互相关干扰项，将其表示为Cj，i，不考虑导航数据位的影响，则Cj，i可以进一步化简［13］为

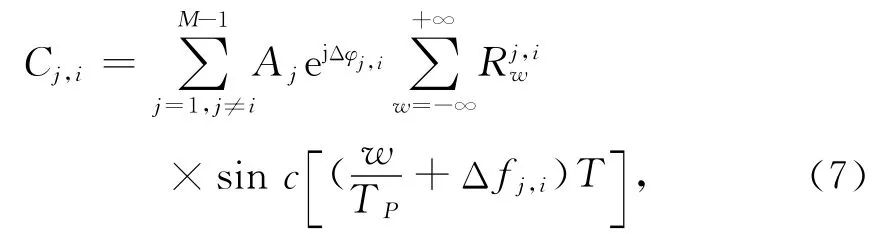
式中，w代表干扰卫星和弱信号卫星间RDC整数kHz的倍数，进一步表示为［13］

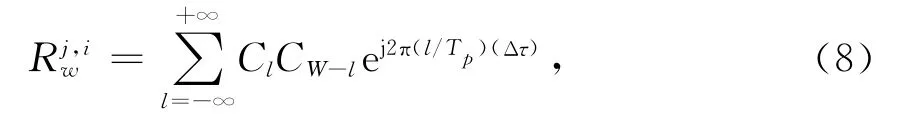
式中：l是一个整数；Δτ＝τi－τj表示本地复现码相对于干扰卫星码的时延；Cl和Cw－l分别是将干扰卫星码和本地复现码表示为傅里叶级数时的对应的傅里叶系数；Tp表示C／A码周期，约为1 ms.

由式（7）可以看出，互相关干扰项的变化特性主要取决于相对多普勒频移Δj，i以及相干积分时间T，取卫星的相对多普勒频移范围为－5kHz至5kHz，以T取10ms为例，互相关峰随Δfj，i的变化特性如图2和图3所示。

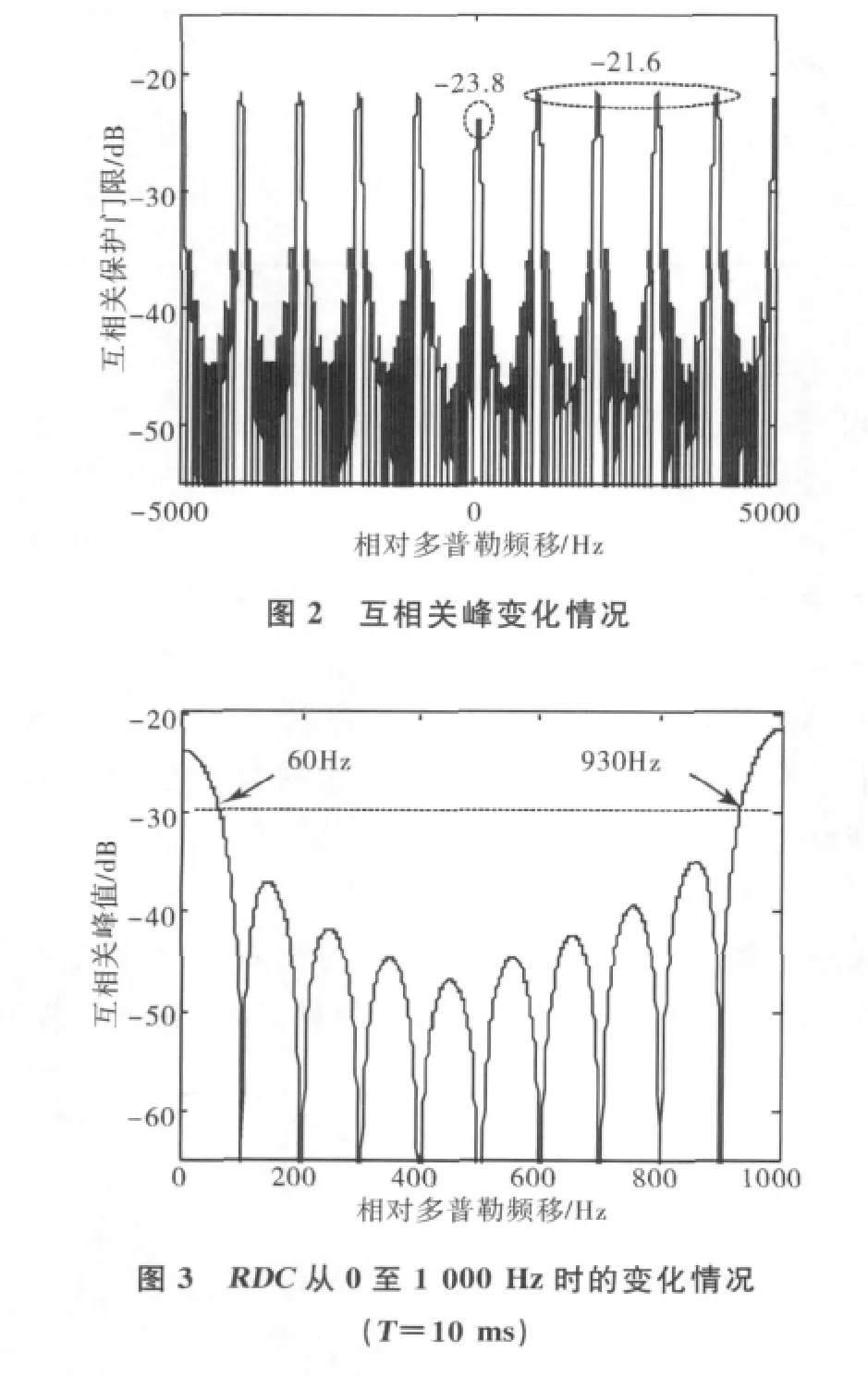
将相干积分时间T进一步延长至20ms，互相关峰随RDC的变化情况如图4所示。

将互相关峰值高于－30dB对应的RDC范围定义为临界多普勒窗，则在图3中，当T取10ms时，第一个局部极小值点出现在相对多普勒频移为100Hz的地方，临界多普勒窗宽度约为120Hz（对应RDC为零）和140Hz（对应RDC为1kHz的整数倍）。而在图4中即当T取20ms时，第一个局部极小值点出现在相对多普勒频移为50Hz的地方，临界多普勒窗宽度约为64Hz（对应RDC为零）和68Hz（对应RDC为1kHz的整数倍），即随着相干积分时间T增加，临界多普勒窗的宽度随之变窄。

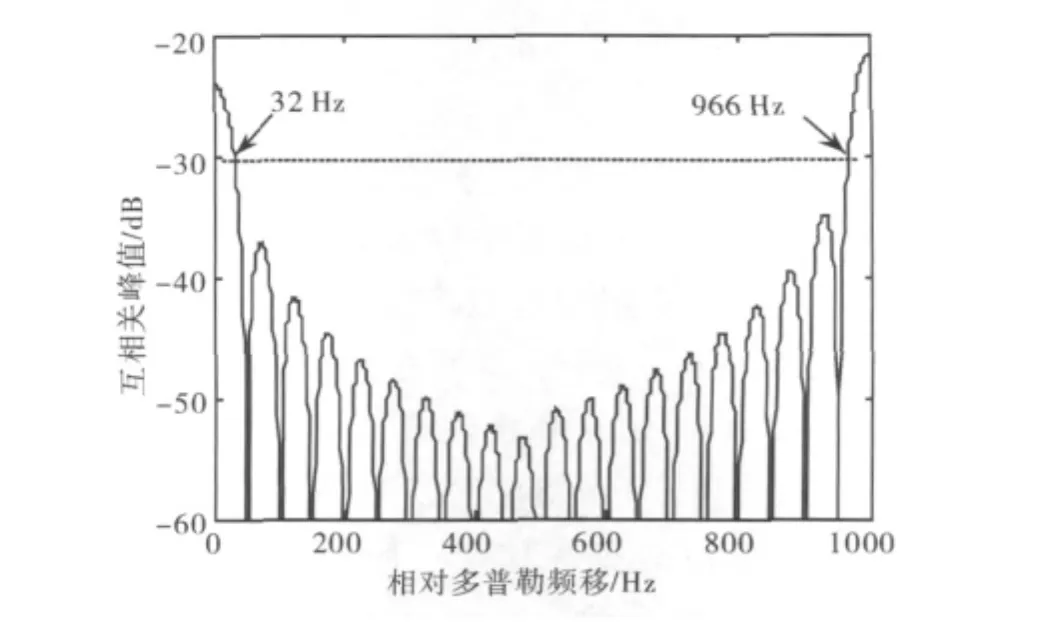
图4 RDC从0～1 000Hz时的变化情况（T＝20ms）

根据上面的结果可以得知，当干扰信号的多普勒频移和弱信号的多普勒频移之差不落在临界多普勒窗中时，互相关干扰就不会对弱信号捕获构成威胁，因此，可以通过分析相对多普勒来检测弱信号的自相关峰，从而实现微弱GPS信号的捕获。

3 基于相对多普勒的检测算法

考虑在对第i颗卫星（弱信号）进行捕获的过程中，接收机分别从多普勒频移和码相位两个维度上对输入信号进行相关搜索，其相关输出结果［14］可以表示为

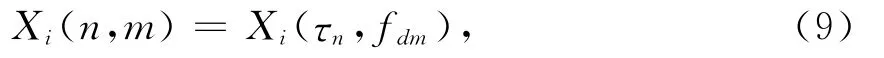
式中：n＝1，……，N是码相位的采样点下标；N为一个C／A码周期内的采样点数，m＝1，…，M为多普勒仓的下标；M为总的多普勒仓数，其大小等于多普勒搜索范围Rfd与多普勒步长ΔfD的比值，文中取ΔfD＝1／（2T）.

不失一般性，将式（9）中的某个多普勒仓记为M0，将m0对应的多普勒仓中的相关峰值对应的码相位采样点下标记为n0，即满足Xi（n0，m0）＝max｛Xi（n，m0）｝，将Xi（n，m0）中去除n0和其所在码片上采样点后的结果用表示，将中的采样点数记为，并把中的相关峰值所对应的码相位采样点下标记为，则对于多普勒仓m0，互相关干扰可以利用式（10）判决［14］

其中：H0和H1分别代表无远近效应和存在远近效应的假设；TNF可以通过给定的I类错误［14］（即当H0为真时检测到远近效应）的发生概率来设定；是（）m0的估计标准差。在H0假设下，（）m0服从自由度为2 NI的χ2分布，可以通过下式计算

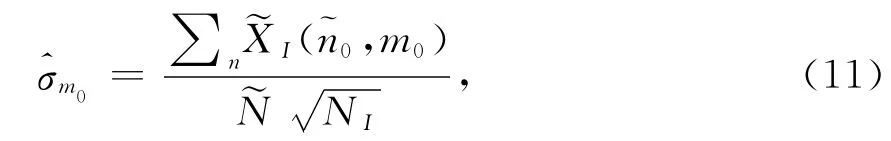
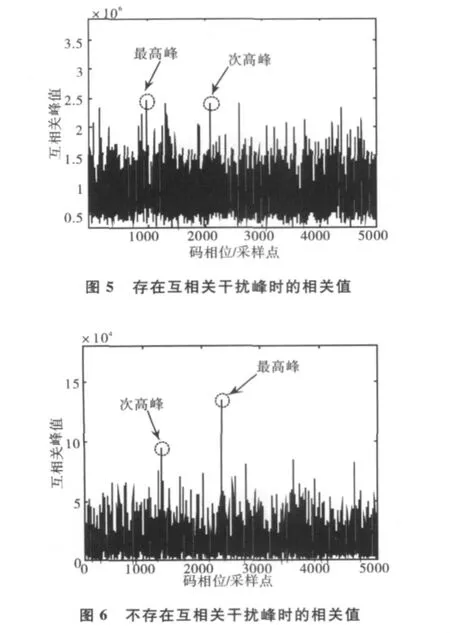
式中，NI为非相干累加次数。图5和图6示出了各自对应着有、无远近效应影响时多普勒仓m0中的相关峰情况，从图中可以看出，当检测到的相关峰为互相关峰时，该干扰峰所在的多普勒仓中的相关最高峰Xi（n0，m0）和次高峰值比较接近，如图5所示；当检测到的峰值为弱信号自相关峰时，其所在的多普勒仓对应的最高峰Xi（n0，m0）明显大于次高峰利用此特性，在对弱信号捕获过程中，可以依次计算每个多普勒仓中对应的式（10），若其大于某个设定的门限，可以认为该相关峰位于正确的多普勒仓中，该相关峰便是弱信号的自相关峰，从而实现微弱信号的捕获。

4 仿真数据验证与分析

采用仿真的强弱卫星信号共存的中频采样数据对上述算法的性能进行验证和分析，中频频率为1.25MHz，采样频率为5MHz，数据共包含三颗卫星，其中3号卫星为强干扰信号，6号卫星和19号卫星均低于3号卫星28dB，属于微弱信号，三颗卫星的主要参数如表1所示，PRN6和PRN19相对于PRN3的RDC分别为500Hz和950Hz，分别代表图4中的互相关峰值远离和接近临界多普勒窗时的情况，为了简化将各卫星的多普勒速率和载波初始相位均设为零。

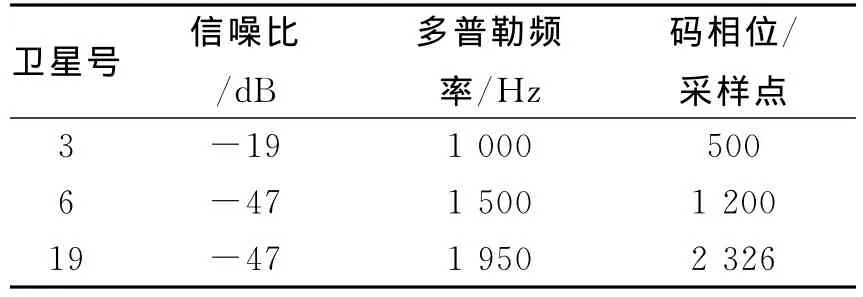
表1 仿真信号主要参数设置

3号卫星使用常规算法便可以成功捕获，6号和19号卫星均采用20ms的相干累积和4次非相干累积，即总的捕获积分时间为80ms，多普勒频率的搜索范围为－5kHz至5kHz，多普勒仓的宽度为25Hz，多普勒仓数＝400个，两个卫星的相关值分布情况分别如图7和图8所示。其中常规检测算法代表采用基于幅值的检测判决算法，新检测算法代表文中介绍的基于相对多普勒分析的检测算法。

从图7（a）和8（a）可以看出，当接收机的本地复现载波与干扰信号（PRN3）的相对载波多普勒偏移为0Hz或者1kHz的整数倍时，互相关干扰项Cj，i就会出现较高的互相关峰，这些峰值远远超过了想要捕获的弱信号的自相关峰，此时若采用传统的基于幅值的检测判决算法，就会导致误捕获，如图7（b）和图8（b）中所示。而采用所介绍的新算法进行检测时，可以找出正确的多普勒频率对应的多普勒仓以及码相位采样点，如图7（c）和图8（c）所示。

图7 PRN6的相关结果

为了进一步评估算法的性能，对算法的捕获成功率进行分析，仿真时令弱信号（即6号、19号卫星）信噪比从－51dB至－45dB变化，每次改变1dB，且信噪比每改变一次，都分别进行100次的中频数据仿真以及捕获试验，捕获成功率R的计算方法如式（12）所示。

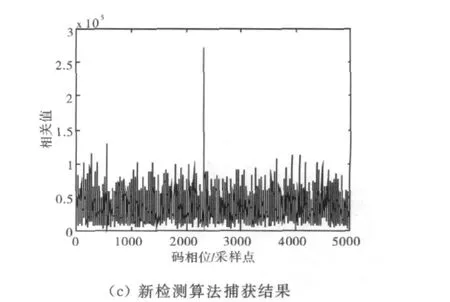
图8 PRN19的相关结果

式中：Ns为成功捕获的次数；Nt为每次试验的总次数（此处取100），得到两颗卫星的捕获成功率随着强弱信号信噪比之差的变化曲线如图9所示。

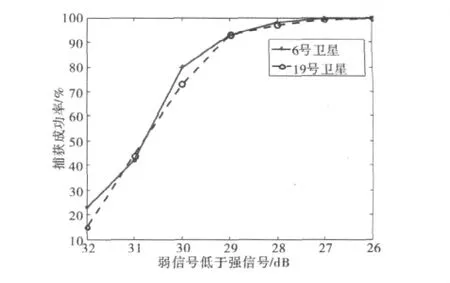
图9 捕获成功率随强弱信号信噪比之差的变化曲线

从图9中可以看出，当弱信号低于强信号29 dB时，该算法依然可以达到93%的捕获成功率。

然而，当弱信号的自相关峰和其与干扰信号间的互相关峰在同一多普勒仓中，或者说强弱信号的RDC在临界多普勒窗中时，该检测算法便无法正确的检测到微弱信号，此时只能进一步采取减去法、投影法等专门的互相关干扰抑制算法来减轻干扰。需要说明的是，出现这种特殊情况的概率比较小，当相干积分时间T取20ms时出现该特殊情况的概率约为10%［15］，并且在辅助GPS、接收机热启动或重新捕获等一些多普勒搜索范围较小的情况下，其发生概率会更小［13］。

5 结 论

基于GPS的C／A码互相关干扰理论模型，详细研究分析了强弱卫星信号的RDC对于互相关干扰的影响，并利用互相关干扰项随着相干积分时间的变化特性，研究了一种新的互相关干扰下的微弱GPS信号的直接检测算法，并利用仿真数据验证了算法的有效性，结果表明：在干扰信号高出弱信号29dB时，利用该算法可以达到超过90%的捕获成功率。

该算法优点是不需要扣除互相关干扰，计算量小，容易实现。缺点是在一些特殊情况下即当强弱信号的RDC落在临界多普勒窗中时单独采用该算法不能正确检测弱信号，此时需要进一步采用专门的互相关干扰抑制算法，在后续的工作中将重点研究此类抑制算法。

［1］ AKOS D M，NORMARK P L，LEE J T，et al.Low power global navigation satellite systems（GNSS）signal detection and processing［C］／／In Proc.ION GPS 2000，Salt Lake City，UT，Sep.2000：784－791.

［2］ GLENNON E P，DEMPSTER A G，RIZOS C，et al.Feasibility of air target detection using GPS as a bistatic radar［J］.Joural of Global Positioning Systems，2005（1－2）：119－126.

［3］ 徐定杰，吕东泽，沈 锋.GPS辐射源的无源雷达两级干扰抑制方法 ［J］.哈尔滨工程大学学报，2012，33（3）：336－341.

［4］ WANG Bo，WU Zhensen，ZHAO Zhenwei，et al.A passive technique to monitor evaporation duct height using coastal GNSS－R.［J］.IEEE Geosci.Remote Sensing Lett.2011，8（4）：587－591.

［5］ ZHANG Jinpeng，WU Zhensen，WANG Bo，et al.Modeling low elevation GPS signal propagation in maritime atmospheric ducts［J］.Journal of Atmospheric and Solar－Terrestrial Physics，2012（80）：12－20.

［6］ 唐卫涛，李 琼，唐 斌.一种新的消除GPS互相关干扰的方法－Q路滤波法［J］.测绘通报，2007（7）：19－22.

［7］ GLENNON E P，DEMPSTER A G.A review of GPS cross correlation mitigation techniques［C］／／In the 2004International Symposium on GNSS／GPS，Sydney，Australia，2004.

［8］ MORTON Y T，TSUI J B Y，LIN D M，et al.Assessment and handling of C／A code self－interference during weak GPS signal acquisition［C］／／In Proc.of ION GPS，Portland，OR，Sep.2003：646－653.

［9］ GLENNON E P，DEMPSTER A G.A novel cross correlation mitigation technique［C］／／ION GNSS，Long Beach，CA，Sep.2005.

［10］ LU Bidong，ZHONG Jie，ZHAO Minjian，et al.A near－far effect canceller for GPS high sensitivity receiver［J］.Position Location and Navigation Symposium（PLANS）2012IEEE／ION，Myrtle Beach，SC，Apr.2012.

［11］ PARKINSON B，SPILKER J.Global positioning system：theory and applications（vol.I）［M］.Washington DC：American Institute of Aeronautics and Astronautics，Inc.，1996.

［12］ VAN DIGGELEN F.Indoor GPS theory ＆implementation［C］／／In Proc.IEEE Position Location ＆Navigation Symposium 2002：240－247.

［13］ QAISAR S U，DEMPSTER A G.Cross－correlation performance assessment of global positioning system（GPS）L1and L2civil codes for signal acquisition［C］／／Radar，Sonar ＆Navigation，IET，2011.

［14］ LOPEZ－RISuENO G，SECO－GRANACOS G.Detection and mitigation of cross－correlation interference in high－sensitivity GNSS receivers［C］／／The 18th Annual IEEE International Symposium on PIMRC，2007.

［15］ QAISAR S U，DEMPSTER A G.Cross－correlation performance comparison of L1 ＆L2CGPS codes for weak signal acquisition［C］／／In Proc.of Int.Symp.on GPS／GNSS，Tokyo，Japan，2008.