两惯性系之间力的一般变换式的推导
徐军令, 路彦峰
在狭义相对论中,粒子相对惯性系的相对论力学的基本方程与经典牛顿力学方程在形式上是一致的。但是在常见的文献中[1-6],没有给出力的一般变换式。本文利用洛伦兹坐标变换,在推导出不同惯性系之间相对论质量变换式的基础上,根据大家所熟知的经典力学中的动量及牛顿第二定律定义式,分析得出力的一般变换式。最后,据此求解了运动电荷对静止点电荷的电场力。
1 狭义相对论中相对论质量及力的变换
如图1所示,狭义相对论中,若坐标系K′(O′x′y′z′)以速度v相对于坐标系K(Oxyz)沿着Ox轴正方向作匀速直线运动,三对坐标轴分别平行,且t′=t=0时原点O′与O重合,则对任一物体P在K′系与K系中的时空坐标及速度变换式遵从洛伦兹变换关系
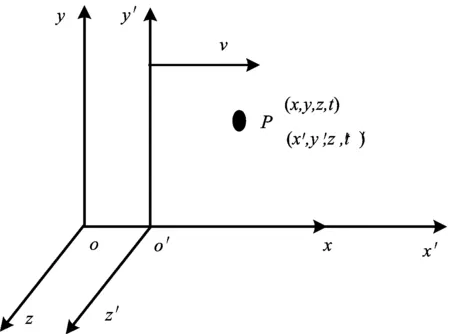
图1 洛伦兹坐标变换
(1)
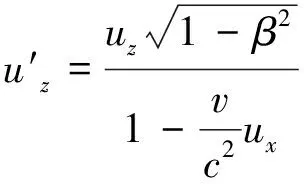
(2)

设物体P在K系中的速度为u,在K′系中的速度为u′,其静止质量记为m0,则P在K系和K′系中的相对论性质量分别为
m=γum0,m′=γu′m0
(3)
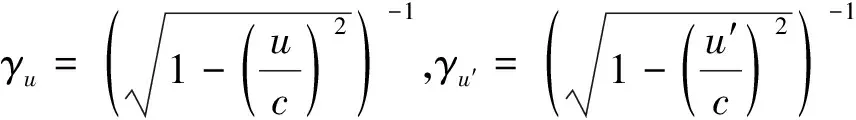
将式(2)代入γu′表示式并化简可得
将式(4)代入式(3),容易推出K′系和K系中相对论性质量的变换式
(5)
根据式(2)和式(5),即可得出K′系与K系中相对论动量的一般变换式
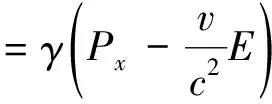
(6)
其中Px=mux,E=mc2
同理可以导出
(7)
将式(6)带入牛顿第二定律数学表示式,可得
(8)
由式(1)中的时间变换式可知
(9)
进而推导出K′系与K系中力的一般变换式
(10)
根据相对论动量和能量关系式
(11)
可得
所以
(12)
所以
(13)
类比(10)式,同理可推出
(14)
由上述力的一般变换式可见,在某一惯性系中方向相同的两个力,变换到另一惯性系中时它们的方向一般不再相同,即牛顿第三定律在相对论中一般是不成立的;但是当物体做低速运动时,该力的变换式就过渡为经典牛顿力学范围。
2 运动电荷对静止电荷的库仑力
如图2所示,设源电荷q固定于K′系坐标原点处,检验电荷q′在K系中静止,q′在K系和K′系中的时空坐标分别为(x,y,z,t)和(x′,y′,z′,t′)。在K′系中,q保持静止,q′处于运动状态,q对q′的电场力可以直接由库仑定律求解
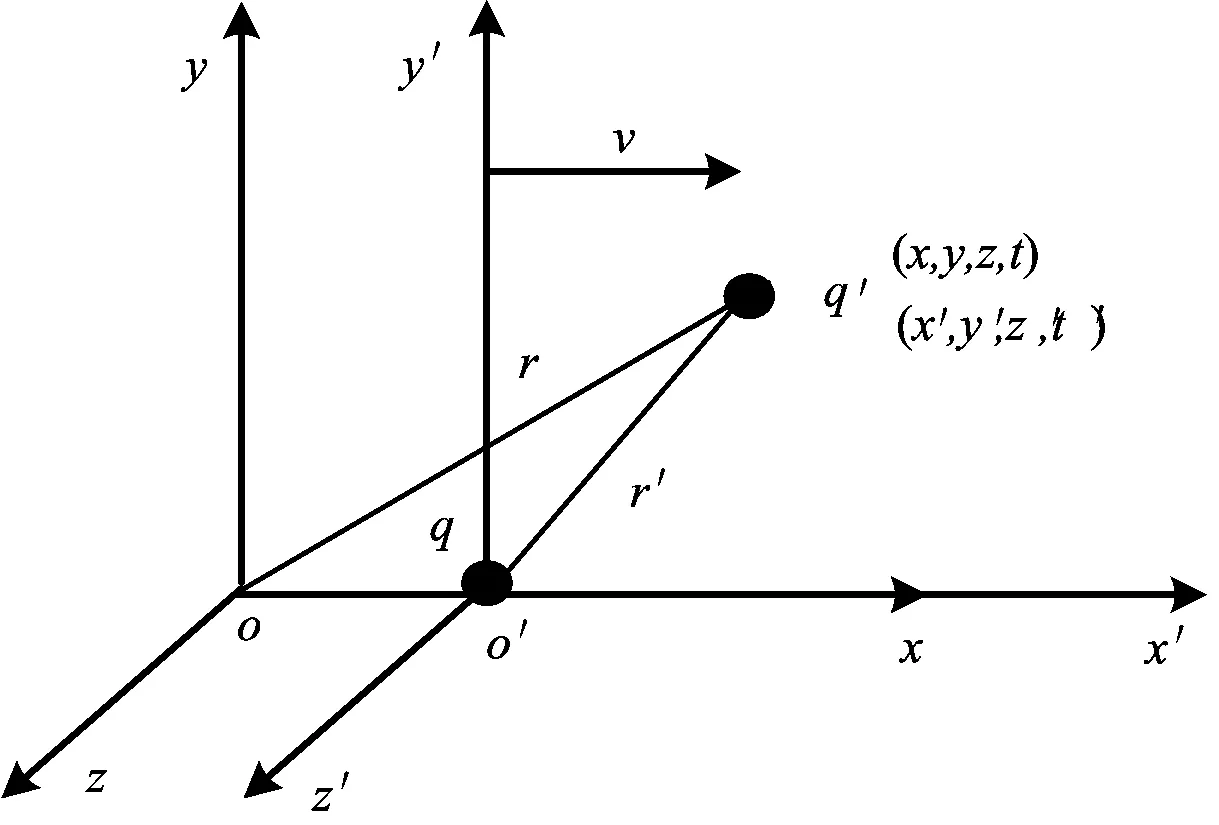
图2 两点电荷的时空坐标
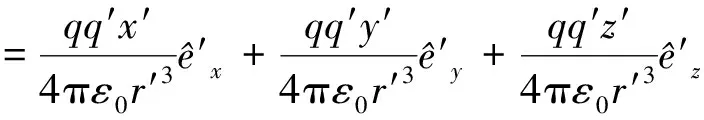
(15)
由于q′在K系中保持静止,其速度u=0。根据K′系与K系之间力的变换式(13)、(14),可知
(16)
由式(15)和式(16)可知
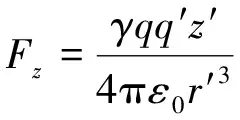
(17)
根据相对论的长度收缩效应可知
x′=γx,y′=y,z′=z
(18)
则有
(19)
将式(18)、(19)带入式(17),则K系中q对q′的电场力为

(20)

3 结论
本文在推导出了两惯性系之间相对论质量、相对论动量变换式的基础上由经典力学中的牛顿第二定律方程推导出了力的一般变换式。然后根据该变换式求解了运动点电荷对静止点电荷的电场力。力的变换式的推导过程简单、易于理解。该力的变换式可以看做是对狭义相对论有关力的变换的教学的一个较好的补充,也对大学生学习和理解相对论力学有积极的意义。
[参 考 文 献]
[1] 郭硕鸿.电动力学(第2版)[M].北京:高等教育出版社,1997.
[2] 李子军,李根全,白旭芳.牛顿力学和相对论力学的协变性[J].大学物理,2002,21(6):22-23.
[3] 胡盘新,汤毓骏,钟季康. 普通物理学简明教程(第2版)[M].北京:高等教育出版社,2007.
[4] 姜晓宜,籍延坤.质点系相对论动量守恒与质点速度的关系[J].大连交通大学学报,2008,29(2):4-6.
[5] 黄锑儒,杨光弟,周红峰.狭义相对论质量、能量和动能概念的研究[J].太原师范学院报,2009,8(2):105-107.
[6] 李玉栋,陆文强,陈 靖,等.大学物理教学中的相对论质量浅议[J].大学物理,2012,31(9):30-31.

