量子粒子群算法优化最小二乘支持向量机及其应用研究
刘 倩
支持向量机是一种基于统计学习理论的机器学习方法。最小二乘支持向量机(LS-SVM)作为支持向量机的改进算法,解决了大样本训练过程中计算速度变慢的问题。已经成功运用于模式识别、信号处理、函数拟合等领域。LS-SVM的性能依赖于模型的参数,对于其参数选择的问题,文献[1]采用遗传算法优化最小二乘支持向量机参数,文献[2]采用粒子群算法对SVM参数进行优化,并运用于变压器故障诊断等。本文用量子粒子群算法(QPSO)优化最小二乘支持向量机模型(LS-SVM)能极大地提高最小二乘支持向量机的寻优能力并对企业的销售管理问题进行寻优,兼顾了公司、营销部的利益以及客户的需求,做到均衡销售,最后使公司的利益最大。
1 最小二乘支持向量机参数优化问题简述
Suykens[3]提出了最小二乘支持向量机(LS-SVM)算法,解决了样本数目大时产生的计算复杂度增加的问题,LS-SVM与标准SVM的主要区别在于损失函数和等式约束上。引入核函数之后,将问题转化到高维空间之后的回归问题表示为:
f(x)=(ω·K(xi,x)+b)
(1)
其目标函数为:
(2)
引入核函数K(x,x)之后的LS-SVM模型为:
(3)
核函数通常选择高斯核函数(RBF核函数):
K(xi,y)=exp(-(x-y)2/2σ2)
(4)
其中,作为一个整体使用的正则化参数γ和核宽度σ两者直接决定最小二乘支持向量机的训练和泛化性能,是最小二乘支持向量机必须调整的两个参数[4]。
2 QPSO算法及其优化LS-SVM过程
2.1 量子粒子群算法
量子粒子群算法[5](Quantum-behaved Particle Swarm Optimization,QPSO)源于粒子群算法,认为粒子具有量子的行为,并且可以在整个可行解空间进行搜索。
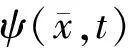
(5)
其中L被定义为:
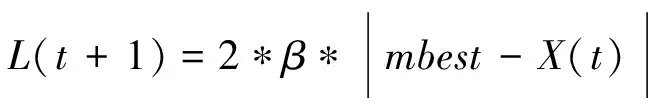
(6)
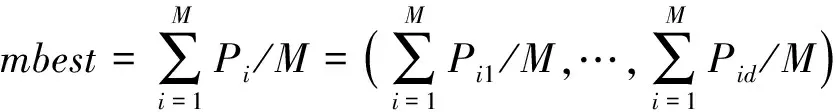
(7)
Pd=φ*Pid+(1-φ)Pgd
(8)

(9)
其中,M为种群中粒子的数目,d为粒子的维数,u和φ为在[0,1]上均匀分布的随机数,mbest为种群中所有粒子的平均最好位置点。Pi和Pg分别表示为粒子i所经历的最好位置和种群中所有粒子所经历的最好位置。β为收缩扩张系数,是QPSO算法中的唯一控制参数,它关系到整个算法的收敛速度,对这个参数的选择和控制是非常重要的,一般取β=(1-0.5)*(MAXITER-t)/MAXITER+0.5,其中MAXITER为最大迭代次数,t为迭代次数。
2.3 QPSO算法优化LS-SVM参数算法过程
本文采用量子粒子群算法优化LS-SVM参数的具体步骤如下:
(1) 设定粒子数目M,量子粒子群的维数d,最大迭代次数MAXITER,迭代的精度设为v,滤波器参数Tf,允许值范围Tf∈(Tfmin,Tfmax);
(2) 最初的迭代次数t=0,利用随机数发生器在控制量可行域内生成M个粒子,形成初始量子粒子群;
(3) 根据LS-SVM算法,再结合核函数,评估出量子种群中每个粒子的适应值,记录当前每个粒子的适应值,更新局部最优值Pi和全局的最优值Pg。本文为获取较为满意的系统动态响应特性,选择目标函数为:
(10)
其中,tr为系统进入稳态需要的时间。将式(10)离散化为:
(11)
式(11)中,e(i)为单位阶跃输入与系统响应的输出之差,T是采样周期,lm为系统达到稳态时要经过的步数。确定lm的方法为:如果连续有几步的误差e(n)都在设定的误差允许范围内,我们就可以认为此时的系统响应已经进入稳定的状态;
(4) 按照式(7)计算出量子粒子群的中心mbest,根据mbest和全局最优粒子Pg,按照式(8)计算出Pi,然后将Pi、mbest代入(9)来更新每个粒子的位置,在式(9)中,当u<0.5时取负,u>0.5时取正;
(5) 判断当前的迭代次数t,是否达到最大迭代次数;若不满足则t=t+1,则转步骤3,直至满足迭代终止条件。
利用量子粒子群算法(QPSO),以MATLAB7.0为实验平台,利用量子粒子群算法对函数F寻优,得到F的最大值。算法流程如下图所示:

图1 QPSO优化算法流程
3 模型的建立
3.1 符号说明
企业都面临着将产品推向市场,销售出去的问题,一般企业生产的产品要通过营销部进行销售,由于企业的生产能力的制约,公司会在满足已签约的销售合同量的基础上,对意向签约量有选择的安排生产,另外企业还希望销售部门再努力多销售一些产品(计划外)。对于所签约的销售合同和意向签约量(计划内),企业根据销售量向营销部发放经费;对于计划外的销售的产品,实行承包制,营销部向企业缴纳利润,产品的生产费由企业承担,与销售有关的给用(如产品的宣传费用等)由营销部承担。
公司计划生产三类10种小家电,其中包括:热水壶(1.5升,1.8升,2升)、豆浆机(0.9升,1.1升,1.3升)、电饭煲(2升,2.5升,3升,3.5升)。三类小家电的年最大生产能力分别为:热水壶5万个;豆浆机6.5万个;电饭煲6.2万个。

表1 公司计划生产三类10种小家电签约情况表
假设变量如下:
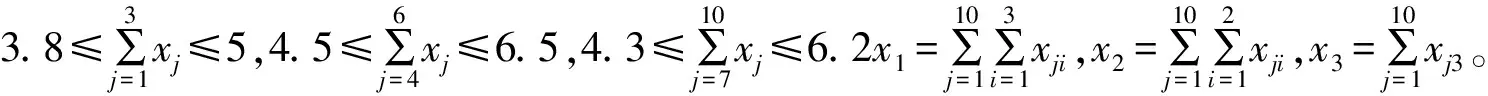
3.2 建立模型
根据以上假设变量建立公司收入模型为:
y=yk-ym-yn+yp
约束条件为:
3.3 解决问题
3.3.1 使公司利润达到最大的方案
为使公司利润达到最大,按最大生产量生产。在满足已签订合约生产量的基础上,对三类产品中盈利最大的单件产品进行生产,根据计算得出,第3、6、8种产品盈利最大,假设这三种产品的意向签约客户已和公司签订正式销售合同。在不超过最大生产量的前提下剩余部分实行承包制,由营销部销售。为使公司利润达到最大的模型为:
y=yk-ym-yn+yp
通过本设计量子粒子群算法(QPSO)优化最小二乘支持向量机模型(LS-SVM)计算得出的结果为:239.5万。
3.3.2 使营销部总收入极大化的方案
除了已经签订合约的产品外,其他在不超过最大生产量的前提下,三种产品中盈利最大的单件产品全部按计划外生产销售。模型为:
z=yn+yk-yp-yl
其中,yk为计划外生产销售额。量子粒子群算法(QPSO)优化最小二乘支持向量机模型(LS-SVM)之后计算结果为:1150.932万。
4 结论
从本设计可以看出,用量子粒子群算法(QPSO)优化最小二乘支持向量机模型(LS-SVM) 进行寻优,利用软件MATLAB7.0建模进行试验,实验结果表明QPSO对LS-SVM之后在销售管理问题上很好地得到了应用,兼顾了公司、营销部的利益以及客户的需求,做到均衡销售,最后使公司的利益最大。
[参 考 文 献]
[1] 王克奇,杨少春,戴天虹,等.采用遗传算法优化最小二乘支持向量机参数的方法[J].计算机应用与软件,2009(7):109-111.
[2] 宋初一.基于最小二乘支持向量机及粒子群优化的特性选择算法研究[D].长春:吉林大学,2008.
[3] 刘江华,程君实,陈佳品.支持向量机训练算法综述[J].信息与控制,2002,31(1):45-50.
[4] 袁小芳,王耀南,孙 炜.基于遗传算法的模糊支持向量机网络控制[J].信息与控制,2005,34(2):205-208.
[5] 周日贵.量子神经网络模型研究[J].南京:南京航空航天大学,2008.15-16.
[6] 王 璋,冯 斌,孙 俊.含维变异算子的量子粒子群算法[J].计算机工程与设计,2008,29(6):1478-1480.
[7] 吕 强,俞金寿.量子神经元结构设计及其应用[J].控制与决策,2007,22(9):355-359.
[8] 孙德山.支持向量机分类与回归方法研究[J].计算机应用与软件,2008,25(2):84-85.
[9] Nello cristianini.john shawe-taylor.An introduction to support vector machines and other kernel-based learning methods[M].BEIJING.publishing house of electronics industry.2004.

